释水条件下黏土层沉降滞后问题研究

徐海洋，任志刚

(中国电建集团成都勘测设计研究院有限公司，成都 610072)



释水条件下黏土层沉降滞后问题研究

徐海洋，任志刚

(中国电建集团成都勘测设计研究院有限公司，成都 610072)

摘要：由于含水层系统中各分层透水性的差异，在含水层系统释水过程中，各分层的沉降对水头响应表现出差异性。结合之前研制的地面沉降试验装置，通过大量试验数据的分析研究释水条件下黏土层变形的滞后，并定义了延迟指数的概念，验证了Leake得出的水头下降造成的最终压缩的93%是在滞后时间段内发生的结论。

关键词：释水；沉降；滞后；延迟指数

0前言

地面沉降是指区域性地面高程下降的一种环境地质现象。资料表明世界绝大多数的地面沉降都发生在地下水储量丰富但地层未完全固结的软弱地质区，该类区域通常含有高渗透率、低压缩性的砂或砾石含水层和低渗透率、高压缩性的黏土弱透水层[1]。

由于含水层系统中各分层透水性的差异，在含水层系统释水过程中，各分层的沉降对水头响应表现出差异性，透水性越好完成沉降时间越短，透水性越差完成沉降所需的时间越长。因此，将这种沉降对水头响应表现出的差异性现象称为沉降的滞后效应。国内学者研究含水层的滞后效应主要是从20世纪90年代开始，以南京大学薛禹群院士、张云、吴吉春、吴剑锋、叶淑君等为代表。薛禹群、张云等认为黏土层变形存在的迟后效应主要和黏土的渗透系数、蠕变性以及水位变化模式有关。国外研究含水层的滞后效应以Leake为代表。Leake认为夹层大多都由细颗粒的物质(如淤泥、黏土等)组成，垂向渗透系数一般较低，因而在周围含水层的水头发生变化时，夹层中的水头平衡通常滞后于周围含水层的水头变化[2-4]。

本文在前人研究的基础上，结合研制的地面沉降试验装置，通过大量试验数据的分析研究释水条件下黏土层变形的滞后。

1延迟指数概念的提出

在《释水条件下地面沉降的滞后效应试验研究》(岩石力学与工程学报,2011,增刊2.)一文中研究了黏土层的变形滞后于水位的变化和黏土层的变形滞后于孔隙水压力的消散，发现II黏土层和III砂层的变形都滞后于水位的变化，但黏土层沉降的滞后时间远远大于砂层。也就是当砂层不再产生沉降的时候，黏土层的变形还在继续，即在整个含水层系统中黏土层的变形滞后于相邻砂层的变形[5]。为了描述黏土层的变形相对于砂层的滞后，我们将黏土层的相对变形量与砂层的相对变形量的比值称为黏土层变形的延迟指数，记为Di，无量纲。

(1)

式中：S黏为黏土层的变形量；S黏为黏土层的厚度；S砂为砂层的变形量；S砂为砂的厚度。经过变化，式(1)也可写成

(2)

式中：C=S砂/S黏为常数。

2延迟指数计算与分析

以1-3号试样第1组试验为例，试验数据如表1所示。

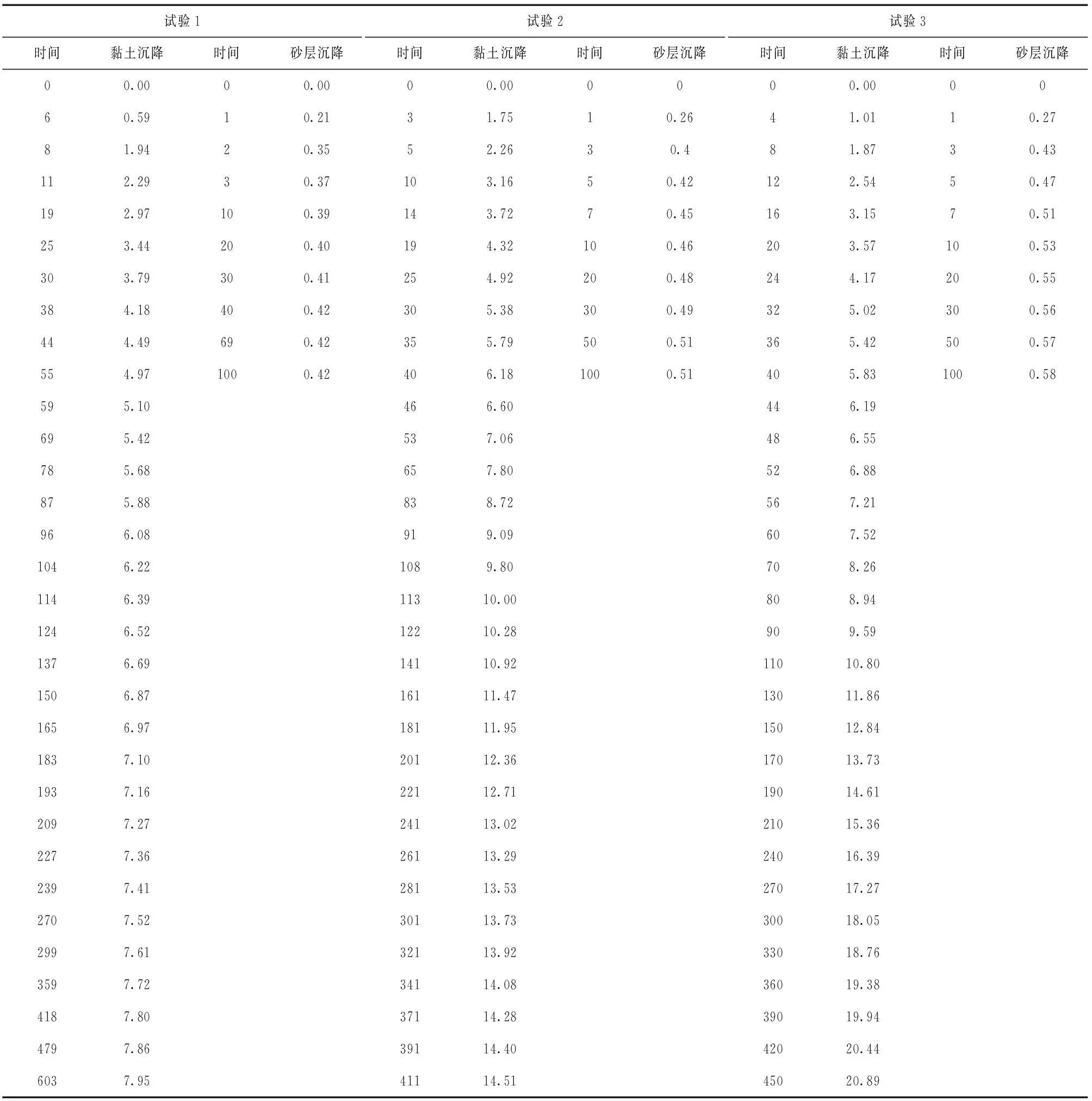
表1　号试验黏土层和砂层沉降量　时间/min；沉降/mm

黏土层变形的延迟指数如图1所示。

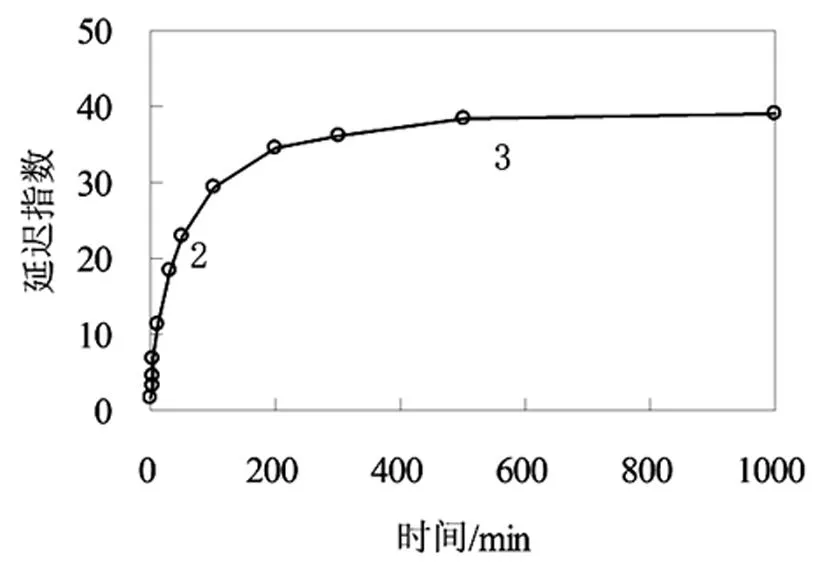
(a)1号试样

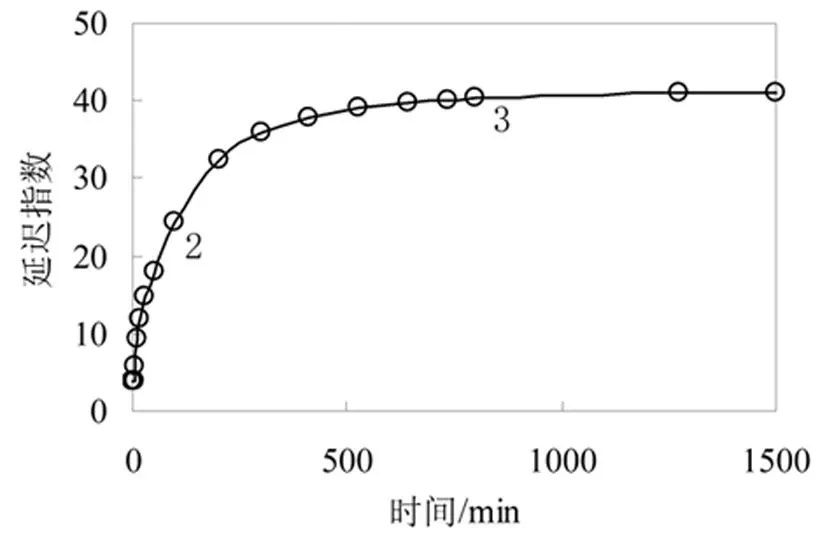
(b)2号试样

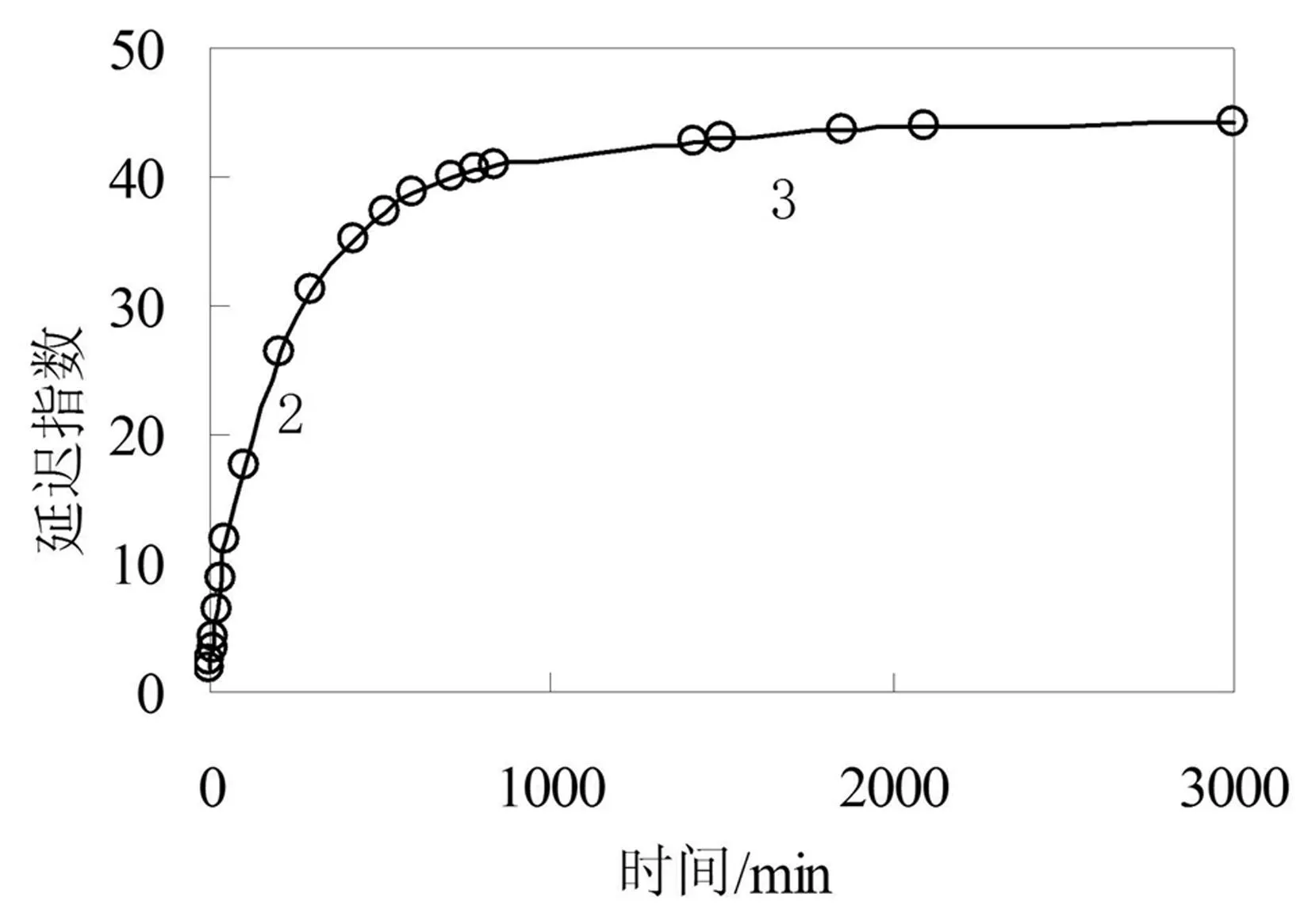
(c)3号试样

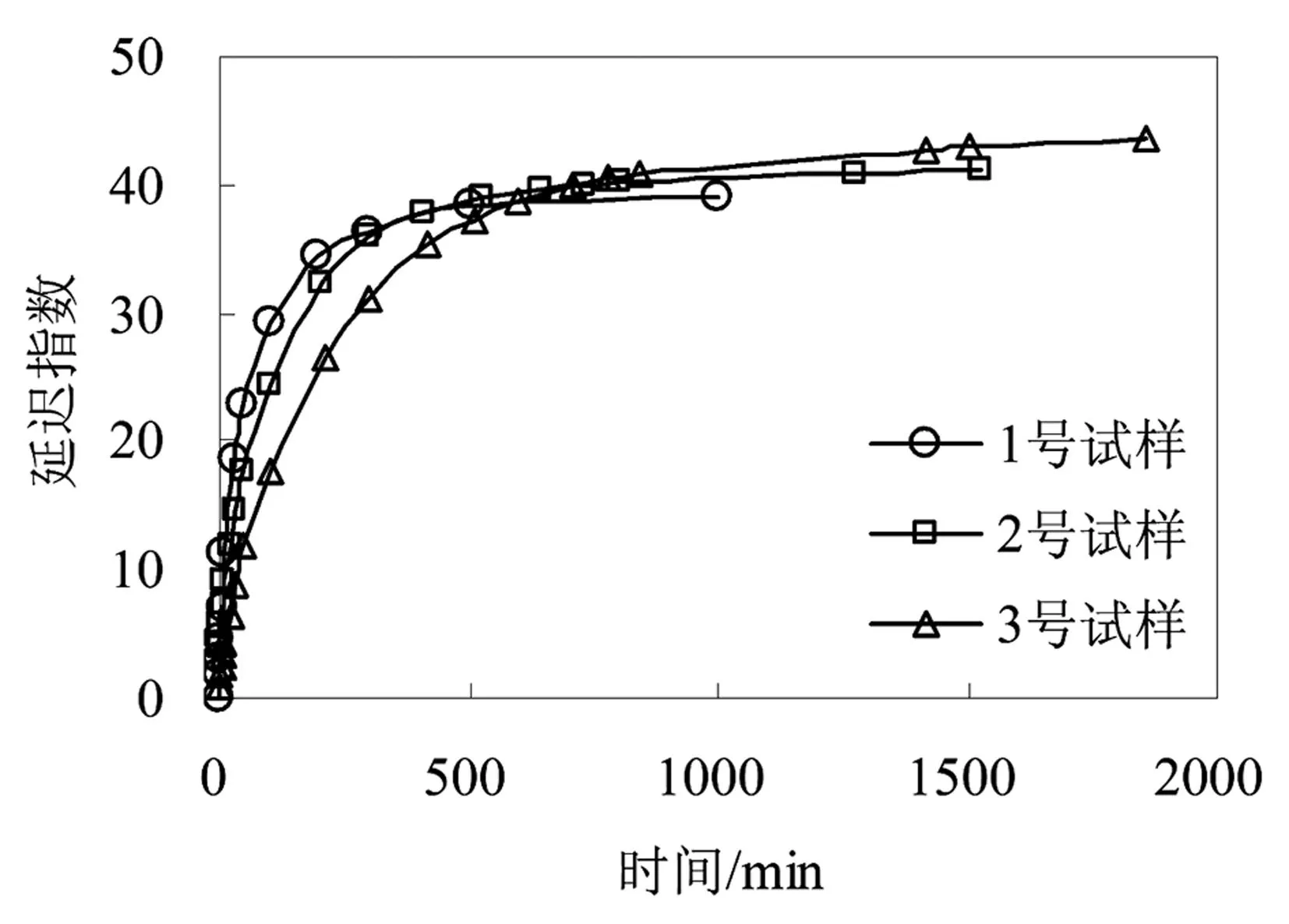
(d)试样1、2、3对比

从图1得出黏土层变形的延迟指数随着沉降的进行而逐渐变大，变化曲线呈现出明显的非线性特征。将图1前面一段(0~10 min)放大，如图2所示。

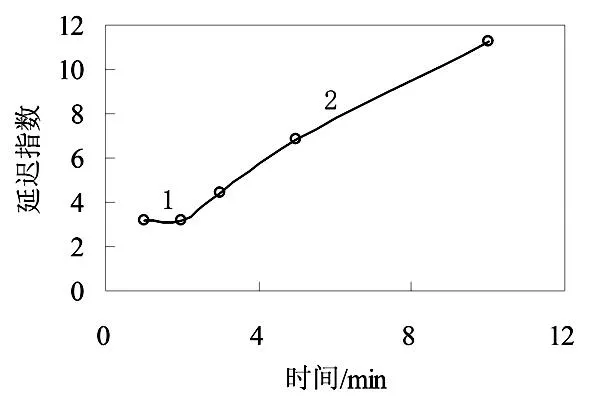
(a)1号试样

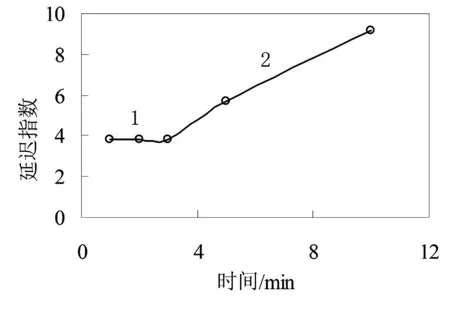
(b)2号试样

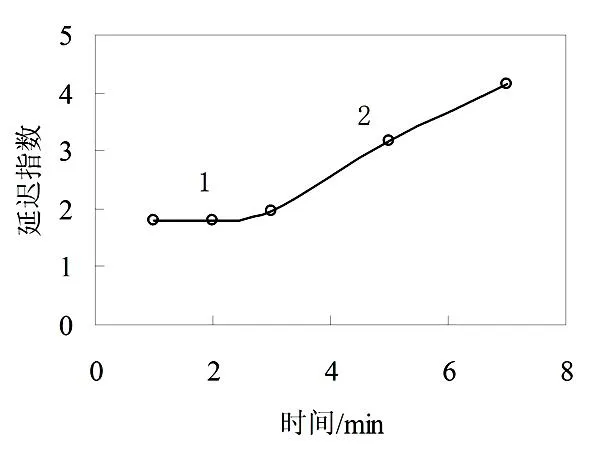
(c)3号试样

从图1、2可以清楚的看出延迟指数随时间变化曲线随时间可分为3段。第1段持续时间较短，斜率较小，几乎为一水平线；第2段持续时间较长，斜率较大，几乎为一直线；第3段持续时间较长，斜率逐渐减小，最终趋于0。

将图1中的时间取对数得到图3，从图3能更加清晰的看出延迟指数随时间变化曲线的分段性。

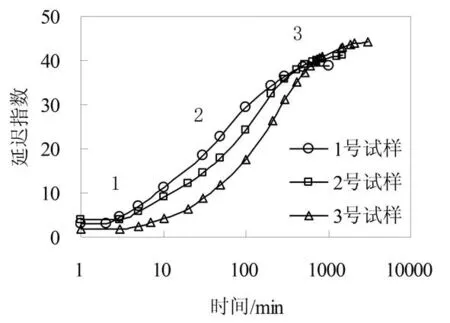
图3　黏土层变形的延迟指数随对数时间变化曲线

通过《释水条件下地面沉降的滞后效应试验研究》一文中地面沉降对水位变化的响应试验得出：在含水层开始释水的前几分钟，砂层和黏土层均产生沉降，即：S砂、S黏都在变化，且变化基本为线性，如图4所示。通过式(1)可以得到Di为定值，所以延迟指数随时间变化曲线的第1段基本为一水平线。与黏土层的沉降相比，砂层的沉降历时较短，所以第1段持续时间较短。当砂层的沉降完成时，S砂/S砂为定值，而黏土层沉降还在继续，S黏/S黏持续增大。第2段反映了黏土层的主固结过程，即黏土层中超静孔隙水压力消散完全的过程。当黏土层中超静孔隙水压力消散完全后黏土层还会发生次固结，即产生蠕变。和主固结沉降量相比，黏土的蠕变量非常小，即S黏/S黏增加的非常缓慢，所以第3段斜率逐渐减小，最后趋于0。

3延迟指数与沉降的关系

从延迟指数的定义可以看出黏土层的沉降与之有密切的关系。按照延迟指数的3个阶段将黏土层的沉降分为相应的3段。每一阶段的起始延迟指数和沉降量如表2所示。

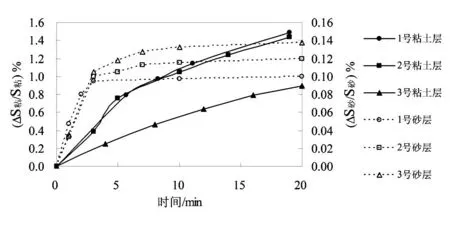
图4　试验前期黏土层、砂层的

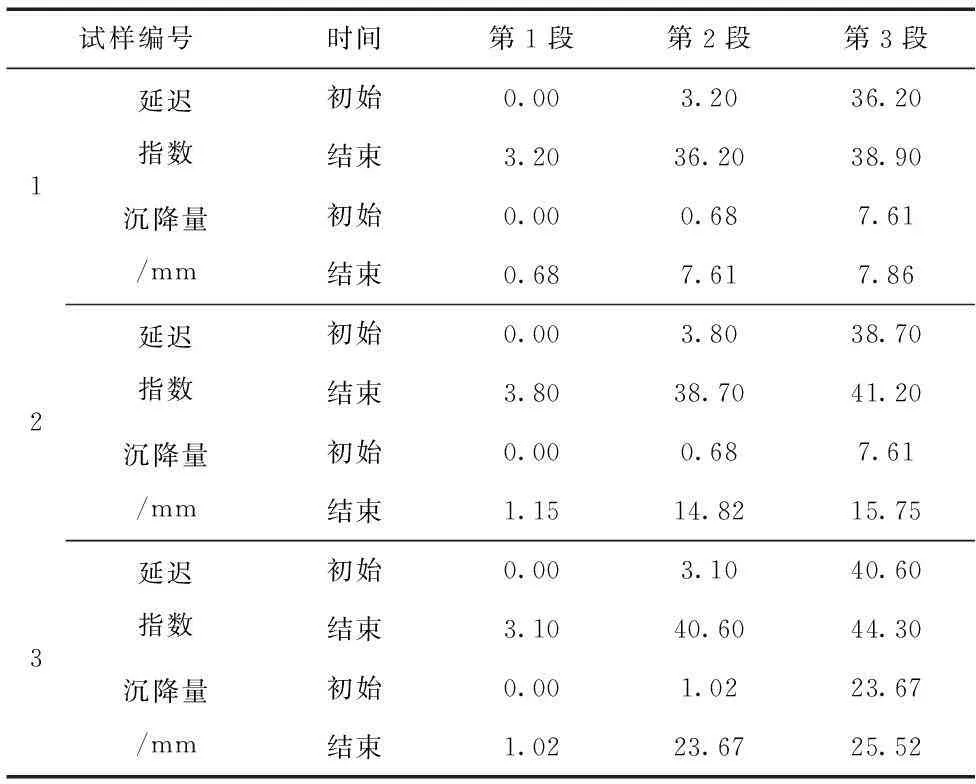
试样编号时间第1段第2段第3段1延迟指数初始0.003.2036.20结束3.2036.2038.90沉降量/mm初始0.000.687.61结束0.687.617.862延迟指数初始0.003.8038.70结束3.8038.7041.20沉降量/mm初始0.000.687.61结束1.1514.8215.753延迟指数初始0.003.1040.60结束3.1040.6044.30沉降量/mm初始0.001.0223.67结束1.0223.6725.52

从表2中可以看出第2段延迟指数的增量和沉降量要远远大于第1、3段，每一段的延迟指数的增量和沉降量占整个沉降过程的百分比如表3所示。

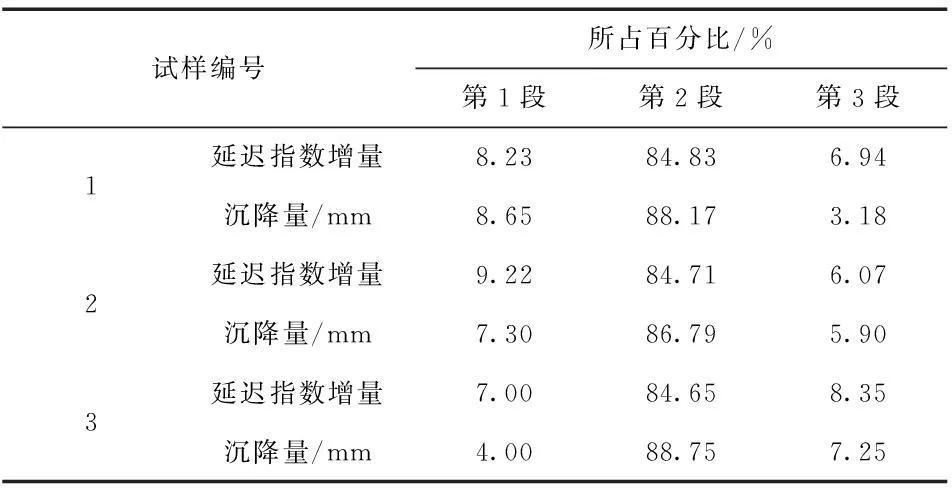
表3　各个阶段延迟指数增量和

从表3可以看出，第1阶段的延迟指数的增量约占延迟指数最终值的8.1%，与其相对应的第1阶段的沉降量约占总沉降量的6.6%；第2阶段的延迟指数的增量约占延迟指数最终值的84.8%，与其相对应的第2阶段的沉降量约占总沉降量的87.9%；第3阶段的延迟指数的增量约占延迟指数最终值的7.1%，与其相对应的第2阶段的沉降量约占总沉降量的5.5%。

从沉降的角度来看，黏土层的主固结变形发生在第1、2段，即超静孔隙水压力完全消散的过程，主固结变形量约占最终沉降量的94.5%(6.6%+87.9%)。在主固结完成时，黏土层的延迟指数约为最终值的92.9%(8.1%+84.8%)。也就是说当延迟指数达到最终值的92.9%时，主固结基本完成[6]。

从滞后的角度来看，当承压含水层水头降低，承压含水层和黏土层都会产生沉降(图4)。在第1段中，S砂、S黏都在变化，且变化基本为线性，由式(1)可以得到延迟指数基本为定值，在这个阶段黏土层变形相对于相邻砂层变形的滞后效应并不明显。黏土层的变形滞后于相邻砂层的变形主要发生在第2、3段，在这两段中砂层基本不再发生沉降。在第2、3段的时间段内，黏土层的沉降量约占总沉降量的93.4%(87.9%+5.5%)，也就是说黏土层沉降的93.4%是在这个滞后时间段内发生的。

4结论

本文在前人研究的基础上，结合研制的地面沉降试验装置，通过大量试验数据的分析研究释水条件下黏土层变形的滞后，得出以下结论：

1)提出了黏土层延迟指数的概念。

2)合理解释了在沉降过程中延迟指数曲线的分段性。

3)验证了Leake得出的水头下降造成的最终压缩的93%是在滞后时间段内发生的结论。

参考文献：

[1]柳志锡.复杂含水地层之抽水沉陷行为[D].新竹：台湾交通大学，2004.

[2]施小清，薛禹群，吴吉春，张云，于军，朱锦旗.常州地区含水层系统土层压缩变形特征研究[J].水文地质工程地质，2006(03):1-6.

[3]张云，薛禹群，叶淑君，吴吉春，李勤奋.地下水位变化模式下含水砂层变形特征及上海地面沉降特征分析[J].中国地质灾害及防治学报，2006，17(03):103-109.

[4]薛禹群，张云，叶淑君，等.我国地面沉降若干问题研究[J].高校地质学报，2006，12(02):153-160.

[5]张云，薛禹群.抽水地面沉降数学模型的研究现状与展望[J].中国地质灾害及防治学报，2002,13(02):1-6.

[6]于军，吴吉春，叶淑君，吴剑锋，王光亚，张云.苏锡常地区非线性地面沉降耦合模型研究[J].水文地质工程地质，2007(05):11-16.

[作者简介]徐海洋(1981-)，男，河南信阳人，工程师；任志刚(1972-)，男，四川成都人，高级工程师。

[收稿日期]2015-05-08

中图分类号：P642.26

文献标识码：B

文章编号：1007-7596(2015)08-0026-04