对单密钥Even-Mansour分组密码的简单安全性证明

罗宜元，　苏庆刚2，

(1. 上海电机学院 电子信息学院, 上海 201306;

2. 华东师范大学 信息科学技术学院, 上海 200241)

对单密钥Even-Mansour分组密码的简单安全性证明

罗宜元1，苏庆刚2，1

(1. 上海电机学院 电子信息学院, 上海 201306;

2. 华东师范大学 信息科学技术学院, 上海 200241)

摘要：Even-Mansour结构是最简单的构造分组密码的方法。利用Kilian-Rogaway的游戏论证方法，给出了单密钥Even-Mansour分组密码的一个简单的不可区分安全性证明，大大简化了之前的一般性证明方法。

关键词：计算机安全; 密码学; Even-Mansour; 分组密码; 不可区分性

收稿日期：2015 - 07 - 03

基金项目：国家自然科学基金项目资助(61402280)；上海电机学院重点学科资助(13XKJ01，A1-1201-14-005)

作者简介：罗宜元(1986 - )，男，讲师，博士，主要研究方向为信息安全和密码学，E-mail： luoyy@sdju.edu.cn

文章编号2095 - 0020(2015)05 -0272 - 05

中图分类号：TP 309.7

文献标志码：A

Abstract：Even-Mansour cipher is the simplest block cipher based on a public permutation. In this paper we propose a simple indistinguishability proof for single key Even-Mansour cipher based on Killian-Rogaway’s game playing method. The proof presented in this paper is much simpler than previous proofs.

Simple Security Proof for Single Key Even-Mansour Cipher

LUOYiyuan1,SU Qinggang2,1

(1. School of Electronics Information Engineering, Shanghai Dianji University,

Shanghai 201306, China; 2. School of Information Science Technology,

East China Normal University, Shanghai 200241, China)

Key words： computer security; cryptography; Even-Mansour; block cipher; indistinguishability

随着计算机网络、云计算、大数据等信息技术的快速发展，人们逐渐享受到互联网的便利，但同时，信息安全问题却愈来愈突出。在信息安全技术中，密码学处于基础性的地位，是信息安全技术的核心，也是攻击者最难攻破的模块。在密码学中，分组密码扮演着基础的角色，其通常被称为密码学原语，很多应用协议方案等都可以基于分组密码算法来实现。由于分组密码应用的广泛性，使得人们对其安全性有着十分严格的要求。整个密码学术界从来没有停止过对分组密码结构的分析。

从设计结构来看，分组密码的常用构造有3种： ① Feistel结构，以数据加密标准(Data Encryption Standard, DES)算法为代表[1]。对于Feistel结构安全性的证明，是由Luby等[2]开始的。②Lai-Massey结构[3]，以FOX算法为代表[4]。Lai-Massey 结构具有与Feistel结构相同的安全界限。③ 迭代式Even-Mansour结构，也即密钥交替密码结构，以高级加密标准(Advanced Encryption Standard, AES)算法为代表[5]。近几年，学术界掀起了对该结构安全性证明的热潮。而该结构最早是基于Even-Mansour结构扩展而来的[6]。

Even-Mansour分组密码是最简单的设计一个分组密码的方法。该密码基于一个公开的n比特置换P，将n比特的明文与一个n比特密钥k1异或后作为P的输入，得到的输出再与另一个n比特密钥k2异或，得到n比特密文。Even-Mansour密码的加密表示为

y=E(x)=P(x⊕k1)⊕k2

相应地，其解密算法表示为

x=D(y)=P-1(y⊕k2)⊕k1

其中，x和y分别为明文和密文；E为加密函数；D为解密函数；P为公开置换，P-1为该P的逆。

Even等[6]认为该结构是最简结构，因为去除k1或k2后该结构将不安全，且很容易对其进行攻击。而Dunkelman等[7]认为该结构并不是最简单的结构，并给出了更简单的单密钥Even-Mansour结构。在该结构中，令k1=k2=k,用一个密钥k就能达到同样的安全界限,该结构被称为单密钥 Even-Mansour结构(SEM)。Even-Mansour结构和单密钥Even-Mansour结构如图1所示。

Dunkelman等给出的安全界限为O(qEqP/2n)，其中，qE和qP分别是攻击者查询E和P的次数。然而，他们的安全性证明仅证明该结构在存在性伪造攻击下的安全性。Bogdanov等[8]证明了t轮迭代式Even-Mansour密码在区分性攻击下的安全界限，即当t≥2时，t轮迭代式Even-Mansour结构的不可区分性为O(q3/22n)，其中，q为攻击者对每一个置换的查询最大次数。随后，Lampe等[9]证明了t轮迭代式Even-Mansour结构的不可区分性为O(qt+2/2t n)。Chen等[10]证明了t轮迭代式Even-Mansour结构所能达到的最好的安全界限为O(qt+1/2t n)。Chen等[11]证明了2轮Even-Mansour结构所能达到的最好的安全界限。这些安全性证明都非常复杂，令人费解。

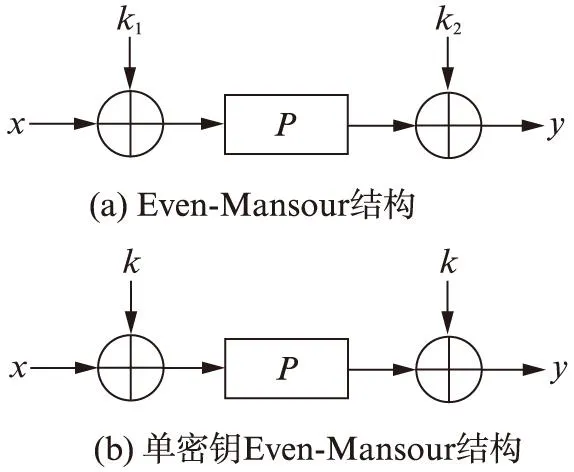
图1　Even-Mansour结构与单密钥Even-Mansour结构Fig.1　Even-Mansour structure and single key Even-Mansour structure

从目前来看，还没有公开文献给出单密钥Even-Mansour结构的详细的不可区分性安全证明。本文基于Kilian-Rogaway的游戏论证方法[12]，给出了单密钥Even-Mansour对于自适应性选择明密文攻击者A下的不可区分性的精确界限qEqP/2n-1，其中，qE和qP分别是攻击者A对E和P进行查询(正向或逆向)的次数。与之前的证明相比，本文大大缩减了篇幅，证明方法也较为简单。

1基本符号术语和不可区分性

1.1　基本符号术语

(1)Pn为在n比特上的所有的(2n)!个置换的集合。

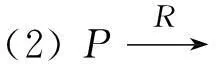
(3) 一个n比特的置换P被称为部分定义的，指该置换当前只被定义了一部分输入及输出值。令Dom(P)表示P当前被定义部分的定义域，令Range(P)表示P当前被定义部分的值域，且令

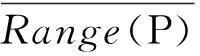
(4) 一个攻击者A称为对(E,P)信息论意义下的自适应性选择明文和密文攻击者，表示A能够对(E,P)里的E和P分别进行自适应性的正向或逆向查询；A的计算能力是无限的，但是A的查询次数是有限制的。

1.2　不可区分性

在本文的不可区分性分析中，攻击者A将要区分两个密码体制： 一个密码体制为(E,P)，也就是现实中的单密钥Even-Mansour密码体制，即P为均匀随机置换，

E(x)=P(x⊕k)⊕k

另一个密码体制为(Π,P),是理想的密码体制，其中，Π和P均为均匀分布的随机置换。A能够对一对预言机(O1,O2)中的O1和O2进行正向或逆向查询，其中，(O1,O2)为(E,P)，或为(Π,P)。A的任务是分别对O1和O2进行正向或逆向查询若干次后，能够判断(O1,O2)究竟是(E,P)还是(Π,P)。

AO1,O2输出为1表示其猜测(O1,O2)为现实世界中的密码体制，也就是(O1,O2)为(E,P)，A的区分优势可以表示为

其中，Pr[Aspan class="emphasis_superscript">E,P=1]为A与(E,P)交互一定次数时输出为1的概率；Pr[AΠ,P=1]为A与(Π,P)交互一定次数时输出为1的概率。

信息论意义下的攻击者A对O1和O2分别进行正向或逆向查询次数最大为qE和qP时，A的区分优势为

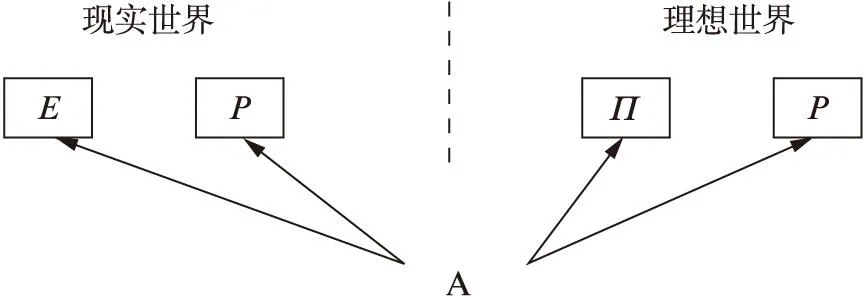
图2　信息论意义攻击者A区分现实世界与理想世界Fig.2　Attacker A distinguishes the real world from an ideal world

2不可区分性安全证明

定理1给定一对预言机(O1,O2)，且(O1,O2)是(E,P)或(Π,P)，则对于任意的、对O1和O2分别进行正向或逆向查询次数最大为qE和qP的信息论意义下选择明、密文攻击的A，其对一个n比特分组长度的单密钥Even-Mansour分组密码(E,P)与(Π,P)区分的概率优势为

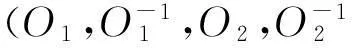
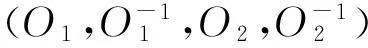
(1) A对O1正向查询x，查询结果如下：

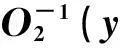
(c) 定义O1(x)=y，返回y。

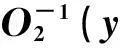
(c) 定义O1(x)=y，返回x；

(3) A对O2正向查询x，查询结果如下：

(b) 定义O2(x)=y，返回y。

(b) 定义O2(x)=y，返回x。

PrIW[AΠ,P=1]=

同样的，假设(O1,O1-1,O2,O2-1)是现实世界，定义现实世界游戏(Real World, RW)的查询规则如下。

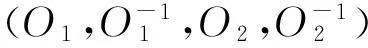
(1) A对O1正向查询x，查询结果如下：

(a) 若O2(x ⊕ k)已定义，则设置标记Bad为True,返回O2(x ⊕ k)⊕ k；

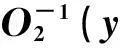
(3) A对O2正向查询x，查询结果如下：

(b) 定义O2(x)=y，返回y。

(b) 定义O2(x)=y，返回x。

此时可明显看出，游戏RW精确地模拟了现实世界的情形。令PrRW[·]为处于RW时相应事件的概率，则有

PrRW[AE,P=1]=

先证明以下结论：

(1)

式(1)表示在Bad为False时，攻击者A将对区分(E,E-1,P,P-1)和(Π,Π-1,P,P-1)无任何概率优势。由IW和RW游戏规则可见，在Bad为False时，用黑体标示的事件并未发生。

(1) 比较在游戏IW和RW中O1的输出，假设此时O1和O2已经分别被查询(正向或逆向)qE和qP次，且Bad仍为False。

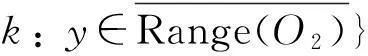
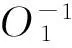
(2) 比较在游戏IW和RW中O2的输出，由游戏IW和RW中第(3)、(4)步可以看出O2在两个游戏中的输出是等概率分布的。

由游戏IW和RW中第(1)、(2)步可见，

PrIW[Bad]=PrRW[Bad]

这是由于当Bad=True时，两者显然是等价的。因此，攻击者A区分(E,E-1,P,P-1)的(Π,Π-1,P,P-1)概率优势可以界定为在游戏IW和RW中的事件Bad为True的概率，形式化的表示为

Adv(A)=

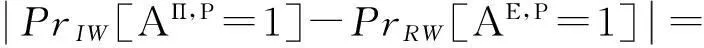
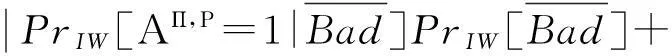
PrIW[AΠ,P=1|Bad]PrIW[Bad]-

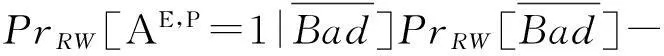
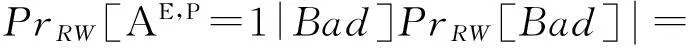
PrIW[Bad]

因此，现在的任务就转为求在游戏IW中事件Bad为True的概率。当A在对O1和O2分别进行查询(正向或逆向)qE和qP次后，对于每一对查询(x,O1(x)),(y,O2(y)),最多会有2个密钥导致事件Bad为True，即

k=x⊕y或k=O1(x)⊕O2(y)

qEqP对查询最多会有2qEqP个密钥k导致事件Bad为True，而密钥k总的数量为2n个，故得出

3结语

本文给出了对单密钥Even-Mansour分组密码的一个简单的不可区分性证明。虽然近些年Even-Mansour结构被广泛研究，但是对单密钥Even-Mansour的不可区分性证明并未见之于公开文献。现有文献对于多轮Even-Mansour的一般性证明过于复杂，本文借鉴了Killian和Rogaway的思想，采用了游戏的方式给出了单密钥Even-Mansour对于自适应性选择明密文攻击下的不可区分性的界限。下一步的工作将是将此证明思路推广到多轮Even-Mansour结构的证明上，期望解决当前学术界对多轮Even-Mansour结构安全性证明过于复杂的问题。

参考文献：

[1]DES.Data Encryption Standard[S].[S.L.]：Springer,1977.

[2]Luby M，Rackoff C.How to construct pseudorandom permutations from pseudorandom functions[J].SIAM Journal on Computing,1988,7(2)： 373-386.

[3]Vaudenay S.On the Lai-Massey scheme[C]∥Advances in Cryptology-ASIACRYPT’99.Berlin： Springer-Verlag,1999： 8-19.

[4]Junod P，Vaudenay S.FOX： a new family of block ciphers[C]∥Selected Areas in Cryptography-SAC 2004.Berlin： Springer-Verlag,2005： 114-129.

[5]Daemen J，Rijmen V.The Design of Rijndael： AES-The Advanced Encryption Standard[M].Berlin： New York： Springer-Verlag,2002： 1-10

[6]Even S，Mansour Y.A construction of a cipher from a single pseudorandom permutation[J].Journal of Cryptology，1997,10(3)： 151-162.

[7]Dunkelman O，Keller N，Shamir A.Minimalism in cryptography： The Even-Mansour scheme revisited[C]∥Advances in Cryptology： EUROCRYPT 2012.Berlin： Springer-Verlag,2012： 336-354.

[8]Bogdanov A，Knudsen L R，Leander G，et al.Key-Alternating ciphers in a provable setting： Encryption using a small number of public permutations[C]∥Advances in Cryptology： EUROCRYPT 2012.Berlin： Springer-Verlag,2012： 45-62.

[9]Lampe R，Patarin J，Seurin Y.An asymptotically tight security analysis of the iterated Even-Mansour cipher[C]∥Advances in Cryptology： ASIACRYPT 2012.Berlin： Springer-Verlag,2012： 278-295.

[10]Chen Shan，Steinberger J.Tight security bounds for key-alternating ciphers[C]∥Advances in Cryptology： EUROCRYPT 2014.Berlin： Springer-Verlag,2014： 327-350.

[11]Chen Shan，Lampe R，Lee J，et al.Minimizing the two-round Even-Mansour cipher[C]∥34th Annual Cryptology Conference： CRYPTO 2014.Berlin： Springer-Verlag,2014： 39-56.

[12]Kilian J，Rogaway P.How to protect des against exhaustive key search(an analysis of DESX)[J].Journal of Cryptology，2001,4(1)： 17-35.