基于不确定离散系统广义H2/H∞底盘集成多目标控制

张家旭　 李　静

(1吉林大学汽车仿真与控制国家重点实验室, 长春 130022)(2中国第一汽车集团技术中心, 长春 130011)

基于不确定离散系统广义H2/H∞底盘集成多目标控制

张家旭1,2李静1

(1吉林大学汽车仿真与控制国家重点实验室, 长春 130022)(2中国第一汽车集团技术中心, 长春 130011)

摘要:提出了一种新的不确定离散时间系统的广义H2/H∞混合控制综合方法,并将其转化为具有较低保守性的线性矩阵不等式组的凸优化问题．考虑车辆前、后轴侧偏刚度参数的不确定性,利用该方法设计底盘集成控制策略,协调控制主动前轮转向系统和主动悬架系统．基于Matlab/Simulink与Carsim联合仿真平台进行典型工况仿真分析．结果表明,设计的车辆底盘集成广义H2/H∞混合控制器能够明显地改善车辆的行驶方向稳定性和防侧翻能力．

关键词:广义H2/H∞混合控制;底盘集成控制;主动前轮转向;主动悬架

doi:10.3969/j.issn.1001-0505.2015.05.002

中图分类号:U461.1

文献标志码:��码: A

文章编号:��号: 1001-0505(2015)05-0871-10

Abstract:A novel method to develop a generalized mixed H2/H∞control for uncertain discrete-time system was proposed, and it was transformed into a convex optimal problem with constraints of linear matrix inequalities with less conservative. Considering the uncertain parameters of cornering stiffness of vehicle front and rear axle, by using this proposed method, the vehicle chassis integrated control strategy was proposed to coordinate the active front wheel steering system and active suspension system. Based on Matlab/Simulink and Carsim platform typical cases were simulated. Simulation results show that the generalized mixed H2/H∞controller for the vehicle chassis integrated system can significantly improve the stability of the traveling direction and anti-rollover capability of the vehicle.

收稿日期:2015-02-03.

作者简介:��: 张家旭(1985—)，男，博士生； 李静(联系人)，男，博士，教授，博士生导师，Liye11129@163.com.

基金项目:国家自然科学基金资助项目(51275206).

Integrated chassis multi-objective control based on generalized H2/H∞

method for uncertain discrete-time system

Zhang Jiaxu1,2Li Jing1

(1State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China)

(2Research and Development Center, China FAW Group Corporation, Changchun 130011, China)

Key words: generalized mixed H2/H∞control;integrated chassis control;active front wheel steering;active suspension

引用本文: 张家旭,李静.基于不确定离散系统广义H2/H∞底盘集成多目标控制[J].东南大学学报:自然科学版,2015,45(5):871-880. [doi:10.3969/j.issn.1001-0505.2015.05.011]

为了提高车辆的主动安全性,许多车辆中安装底盘电控系统(包括主动前轮转向系统、主动悬架系统和电子稳定系统等)．然而,由于轮胎的非线性特性和底盘子系统之间的耦合效应,使这些系统独立工作时产生的综合性能受到限制[1]．为此许多研究者采用底盘集成方式来协调控制这些电控系统，以提高车辆的综合性能[2-3]．Song[4]基于模糊控制和滑膜控制实现主动前轮转向系统、主动后轮转向系统和直接横摆力矩系统的集成控制,以此提高车辆的侧向稳定性和操纵性能．Roshanbin等[5]结合自适应控制和模糊控制，采用主动转向系统和直接横摆力矩控制系统的集成控制策略,以提高车辆的行驶方向稳定性．Yang等[6]基于最优保性能理论设计主动前轮转向系统和直接横摆力矩系统集成控制，以提高车辆的操纵稳定性．Yim等[7]协调主动悬架系统和电子稳定控制系统实现车辆的防侧翻控制．Mando公司以提高车辆的防侧翻能力为目标设计底盘集成控制策略,协调控制直接横摆力矩系统和主动悬架系统[8]．上述文献仅从提高车辆行驶方向稳定性或防侧翻能力单一目标进行底盘集成控制策略研究．然而,车辆处于极限危险工况时,车辆失稳和侧翻情况均可发生．因此,以提高车辆的行驶方向稳定性和防侧翻能力的多目标底盘集成控制将成为研究热点．

基于不确定参数离散系统广义H2/H∞控制，充分考虑被控对象的参数不确定性对系统稳定性的影响,采用被控对象离散化模型进行控制性能的分析与综合,以实现计算机控制．传统的不确定离散时间系统广义H2/H∞控制方法的二次稳定性要求对所有的不确定性参数存在统一的Lyapunov函数,因而得到的稳定性条件具有很大的保守性[9]．本文在文献[10]的基础上,推导出可使用不同Lyapunov函数来处理不确定参数离散系统广义H2/H∞控制问题的线性矩阵不等式组约束条件,从而降低了设计的保守性．利用该方法,考虑车辆前、后轴侧偏刚度参数的不确定性,采用三自由度线性离散化车辆动力学模型作为参考模型,以提高车辆行驶方向稳定性和防侧翻能力为控制目标设计底盘集成控制策略,实现主动前轮转向系统和主动悬架系统的协调控制．最后,利用Matlab/Simlink与Carsim进行典型工况的仿真验证．结果表明,所设计的车辆底盘集成广义H2/H∞控制器具有良好的控制效果．

1不确定离散系统广义H2/H∞控制

不确定离散系统的状态空间描述如下:

(1)

式中，x(k)∈Rn为系统的状态向量;u(k)∈Rm为控制输入;w(k)∈Rp是外部扰动输入;z1(k)∈Rq和z2(k)∈Rr为被调输出;A,B1,B2,C1,C2,D1和D2均为不确定性矩阵,可以表达为某些已知矩阵的凸组合，即

设计状态反馈控制器u(k)=Kx(k),得到相应的闭环控制系统,即

x(k+1)=Acx(k)+B2w(k)

z1(k)=C1cx(k)

z2(k)=C2cx(k)

(2)

Ac=A+B1K

(3)

C1c=C1+D1K

(4)

C2c=C2+D2K

(5)

广义H2/H∞控制问题的任务是:对于凸多面体不确定系统(1),要求设计状态反馈控制器,使得对所有允许的参数不确定,同时满足如下要求:

1) 闭环系统(2)是渐近稳定的.

2) 对于事先给定的参数η>0,使闭环系统(2)的广义H2性能指标满足

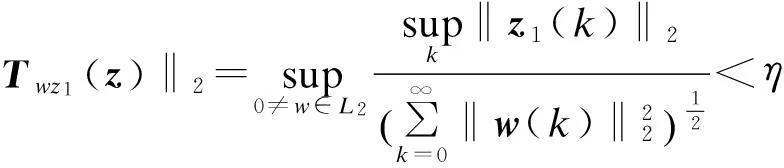
(6)

式中,L2为所有有限能量信号的集合．

3) 存在最小化扰动抑制度γ>0,使闭环系统(2)的H∞性能指标满足

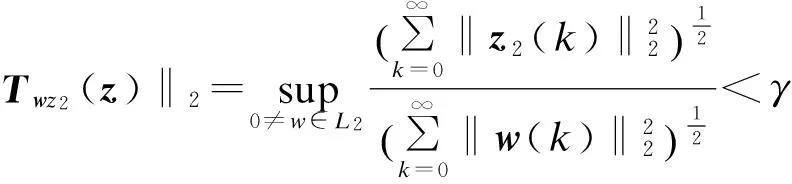
(7)

可将广义H2/H∞控制问题转化为线性不等式组的凸优化问题进行求解,推导过程如下所示．

在引理1和引理2的基础上,根据凸多面体参数不确定系统的内在特性并考虑式(3)～(5),可得到一个具有参数相关Lyapunov函数的广义H2/H∞性能准则．

(8)

(9)

(10)

式中,Ai,B1i,B2i,C1i,C2i,D1i,D2i为系统(1)的顶点矩阵,∀i=1,2,…,N．

(11)

(12)

(13)

(14)

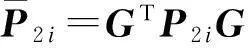
定理2给出了具有参数依赖Lyapunov矩阵的广义H2/H∞性能准则,通过引入松弛变量G,实现了Lyapunov矩阵与系统矩阵之间的解耦,这一特性使得当其应用于凸多面体不确定离散系统时,可得到较低保守性的结果．而且,定理2在描述系统的广义H2和H∞性能指标时,分别采用了不同的Lyapunov矩阵,这将进一步降低设计的保守性．

推论1给定η>0,若优化问题

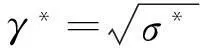
2车辆底盘集成控制

2.1　控制器设计参考模型

以三自由度车辆动力学模型作为车辆底盘集成广义H2/H∞控制器的设计参考模型,如图1所示[11]．该模型包括车辆侧向运动自由度、横摆运动自由度和侧倾运动自由度．

根据图1的参考模型，可列出以下3个平衡方程:

1) 沿y轴力平衡方程为

图1　车辆参考模型

(15)

2) 绕z轴力矩平衡方程为

(16)

3) 绕x轴力矩平衡方程为

(17)

式中,m为整车质量;ms为簧载质量;Ix为簧载质量绕侧倾轴的转动惯量;Iz为整车质量绕垂直轴的转动惯量;γ为车辆横摆角速度;β为车辆质心侧偏角;θ为车辆侧倾角;v为车辆纵向车速;Fy1,Fy2为车辆前、后轴侧向力;a,b为车辆重心至前、后轴距离;ΔFfl,ΔFfr,ΔFrl和ΔFrr为车辆主动悬架系统左前、右前、左后和右后输出作用力;T为轮距;g为重力加速度;k为悬架侧倾角刚度;c为悬架侧倾角阻尼;h为车辆重心到侧倾中心距离.图1中，α1,α2为车辆前、后轴侧偏角;δ1为车辆前轮转向角,该转向角由驾驶员操作产生的前轮转向角δw和主动前轮转向系统输出的前轮转向角Δδw组成．

为缩减主动悬架系统输出作用力对车辆俯仰运动的影响，且考虑车辆前、后轴荷的静态分配,对主动悬架系统前、后输出作用力分配如下:

(18)

(19)

(20)

(21)

式中,ΔFl,ΔFr为主动悬架系统左、右输出作用力．

将式(18)～(21)代入式(17),得到

(22)

忽略轮胎侧向力的非线性,且考虑车辆侧倾时,轮胎和悬架的变形引起的侧倾外倾和侧倾转向因素,得到

(23)

式中,k1,k2为车辆前、后轴侧偏刚度;c1,c2为车辆侧倾外倾与侧倾转向对车辆前、后轮侧偏角的影响系数．

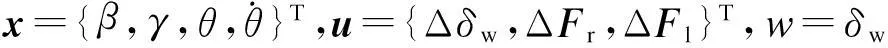
(24)

式中

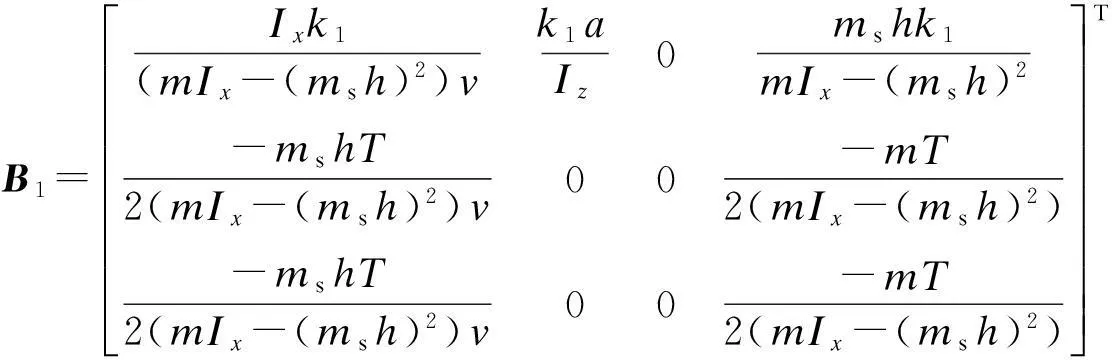
2.2　控制器设计

车辆底盘集成广义H2/H∞控制器设计的目标:在主动前轮转向系统和主动悬架系统执行机构输出允许的范围内,尽可能提高车辆行驶方向稳定性和防侧翻能力．下面将这一控制目标抽象为系统设计的具体性能指标．

1) 车辆的质心侧偏角状态量和横摆角速度状态量反映车辆的行驶方向稳定[12]．因此,提高车辆行驶方向稳定性目标可以转化为使这2个状态量较好地跟踪其期望值,即

(25)

为保证系统性能,取期望的质心侧偏角为βd=0,期望的横摆角速度为

式中,γref为基于图1左侧线性二自由度车辆参考模型计算得到的横摆角速度期望值,即

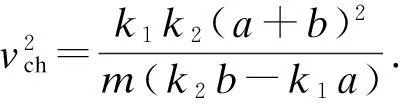
2) 研究发现[13],车辆的防侧翻能力可以用横向载荷转移率Ld表示,定义为

式中,Fzr,Fzl为车辆左、右轮胎的垂向力．

根据达朗贝尔原理,建立如下Ld与车辆状态参数关系:

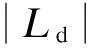
(26)

同时,考虑主动前轮转向系统的最大转向角约束和主动悬架系统的最大输出作用力约束,对执行机构约束如下:

(27)

(28)

(29)

根据式(26)～(29)的约束条件,定义系统约束输出为

(30)

车辆底盘集成系统控制准则可描述为:寻找一个最优控制律,使车辆系统满足全部硬约束条件并尽可能改善车辆的行驶方向稳定性．

(31)

式中

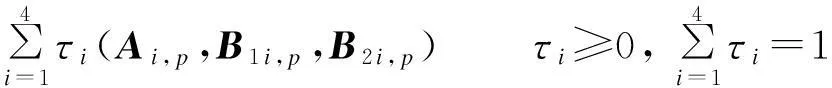
证明系统(31)状态空间描述的系数矩阵A,B1和B2依赖于不确定参数向量ρ={k1，k2},可表示为

(32)

A2a=

A3a=

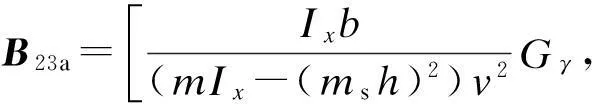
(33)

将不确定参数向量ρ的顶点集代入式(32)，即得到顶点矩阵为

式中

A2p=

A3p=

A4p=

将式(33)代入式(32)即得到结论．证毕．

对系统(31),其顶点矩阵表示的状态方程为

(34)

式中,i=1,2,…,4．

对状态方程(34)进行离散化处理,在采样周期T下离散后的状态空间表达式为

(35)

Gi,p=exp(Ai,pT)

(36)

(37)

i=1,2,…,4

(38)

为保证运算精度,式(36)～(38)采用文献[14]提出的精细时程积分法进行计算．根据计算结果得到系统(31)基于顶点矩阵(Gi,p,H1i,p,H2i,p)的离散化状态空间方程系数矩阵G,H1和H2的凸组合，即

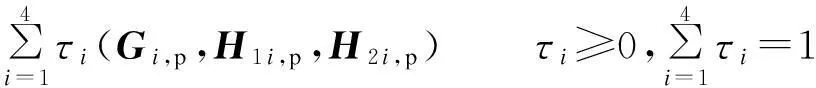
进而得到不确定离散系统状态空间表达式，即

(39)

对于式(39)描述的不确定离散系统，可基于推论1的线性矩阵不等式组的凸优化运算，得到最优广义H2/H∞状态反馈控制律．

3仿真验证

利用Matlab/Simulink与Carsim对上述车辆底盘集成广义H2/H∞控制器进行仿真验证．选取鱼钩试验工况和正弦试验工况,对比有、无底盘集成控制的车辆在2种工况下的行驶方向稳定性和防侧翻能力．车辆的部分参数如表1所示．

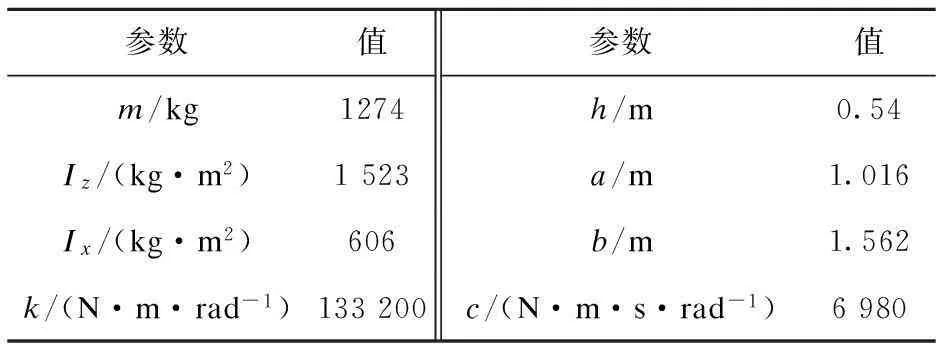
表1　车辆部分参数

3.1　鱼钩试验工况

车辆直线行驶,初始车速为80km/h,路面附着系数为0.8,驾驶员松开加速踏板,前轮转角以720(°)/s匀速增大至8(°),保持0.25s,然后用720 (°)/s匀速反向转动到-8(°)．保持3s,再匀速回到0(°)[15],仿真结果如图2所示．

由图2(a)～(e)可见,无控制时,车辆呈现过多转向特性,质心侧偏角逐渐增大,导致车辆横摆力矩对方向盘转角的敏感性迅速降低,横摆角速度在3.5s后明显偏离其期望值,车辆丧失方向稳定性．采用底盘集成控制后,车辆横摆角速度可以较好地跟踪其期望值,并且质心侧偏角控制在较小的可控范围内．

由图2(f)、(g)可见,与采用底盘集成控制的车辆侧倾角和车辆侧倾角速度相比,无控制时,二者明显变大,车辆更易发生侧翻．

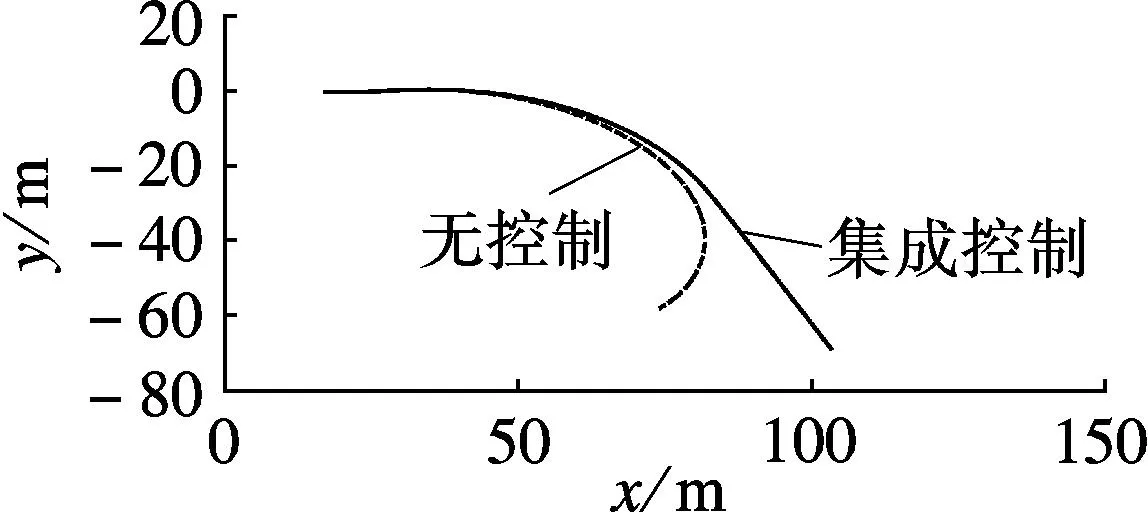
(a) 车辆轨迹

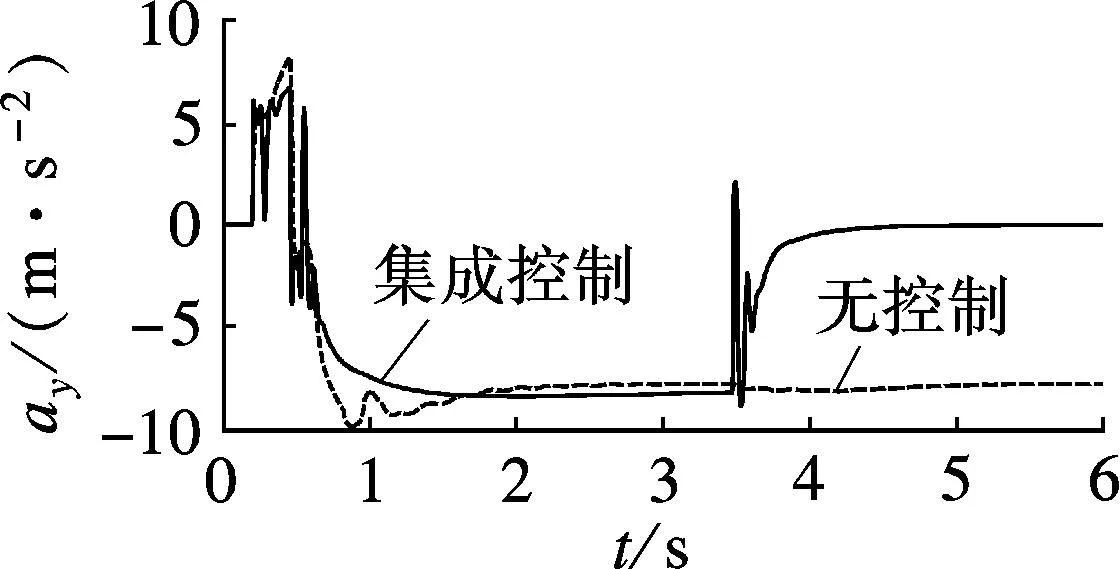
(b) 车辆侧向加速度

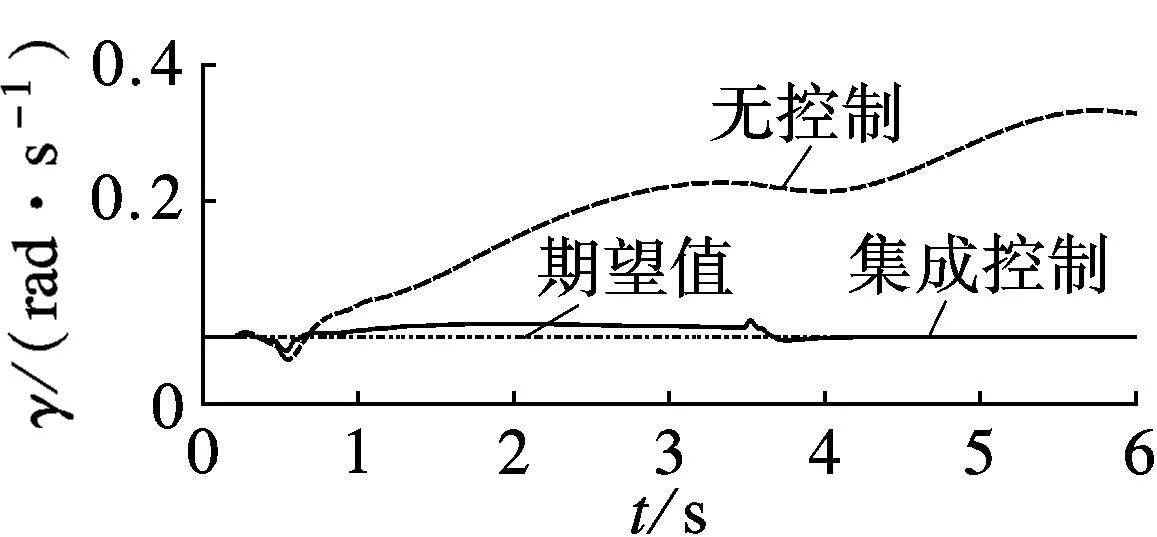
(c) 车辆质心侧偏角

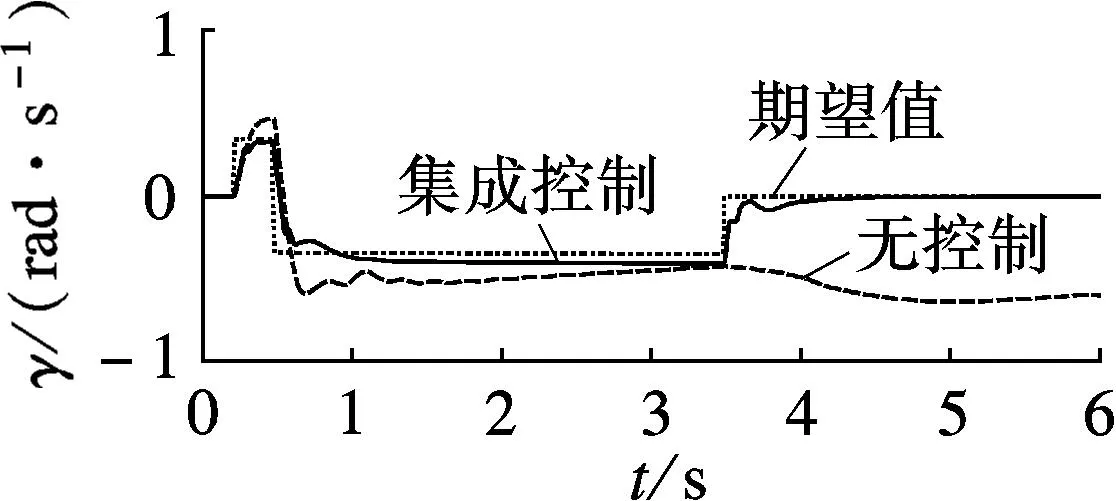
(d) 车辆横摆角速度

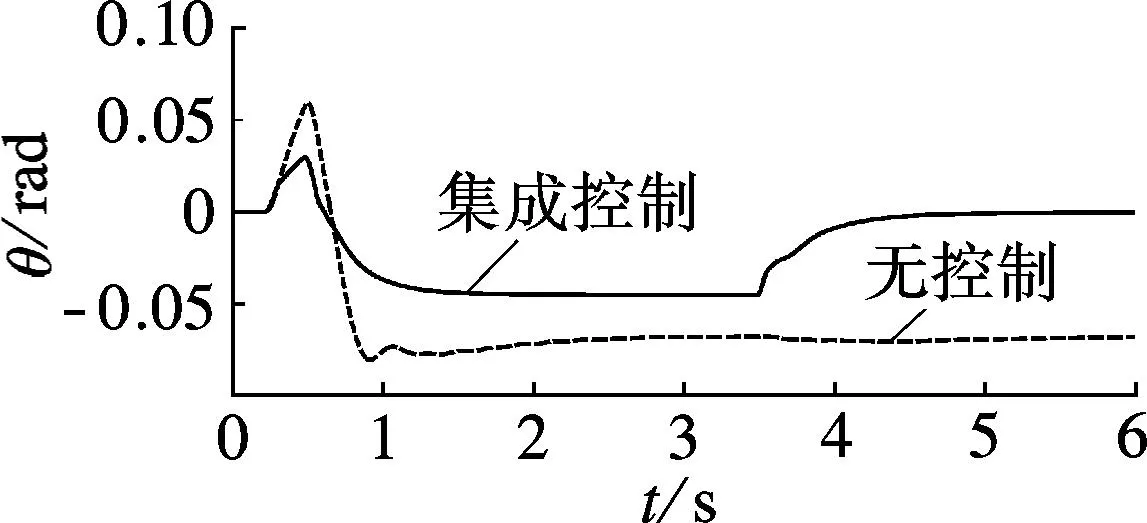
(e) 车辆侧倾角

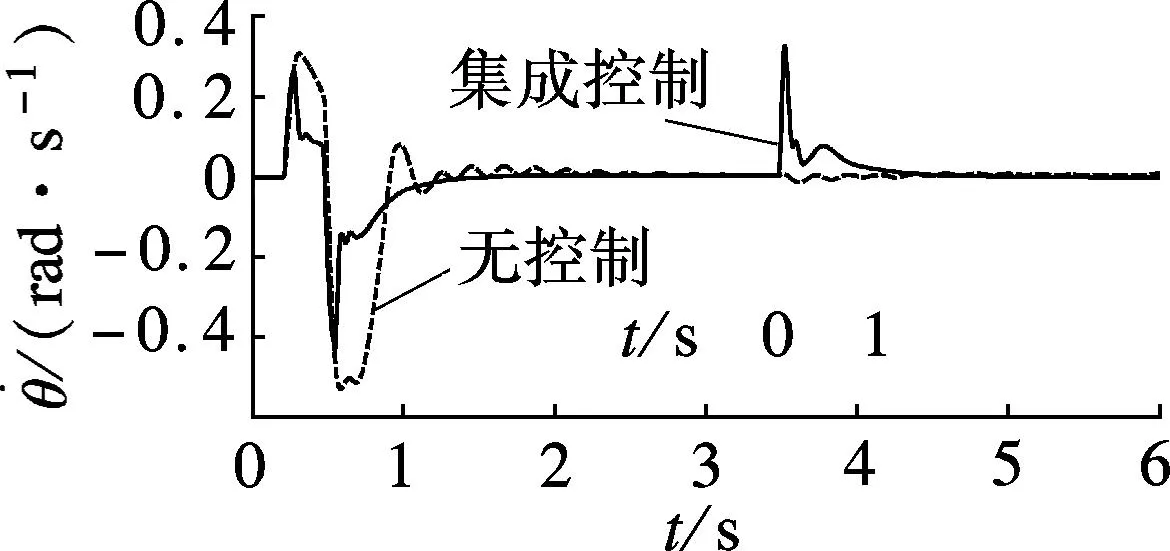
(f) 车辆侧倾角速度

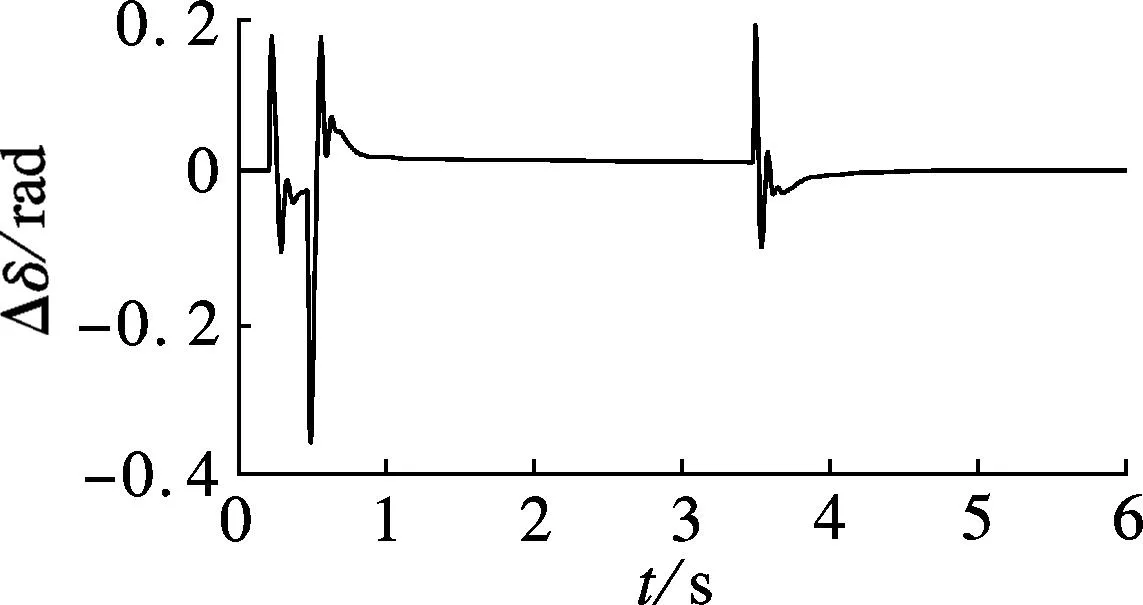
(g) 主动前轮转角

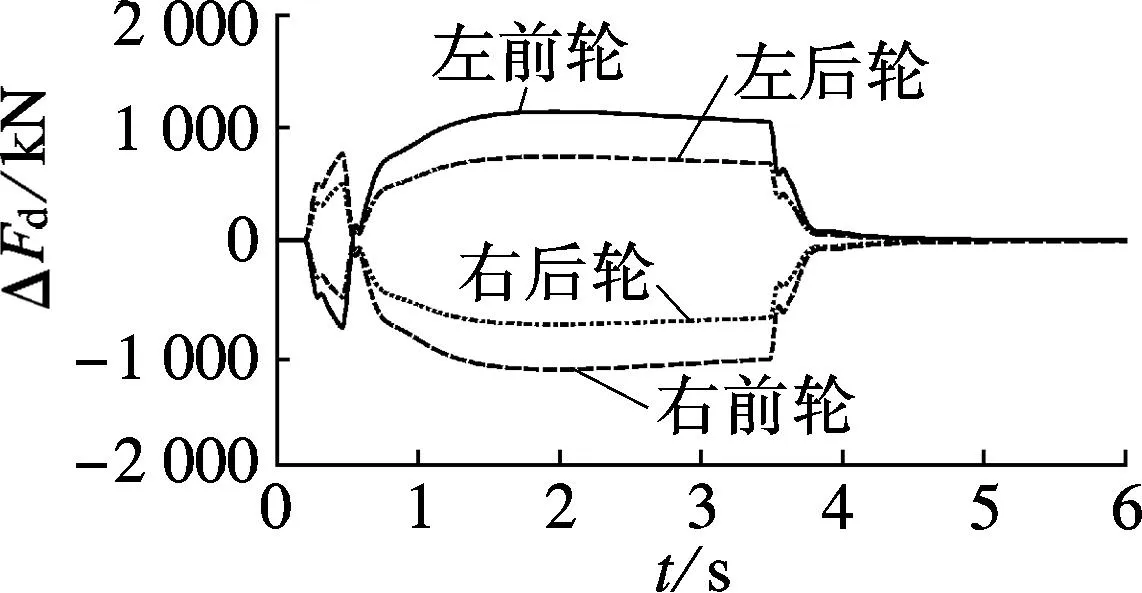
(h) 主动悬架作用力

3.2　正弦试验工况

车辆直线行驶,固定车速为100km/h,路面附着系数为0.8,前轮转角输入幅值为8°,频率为1Hz的正弦信号,仿真结果如图3所示．

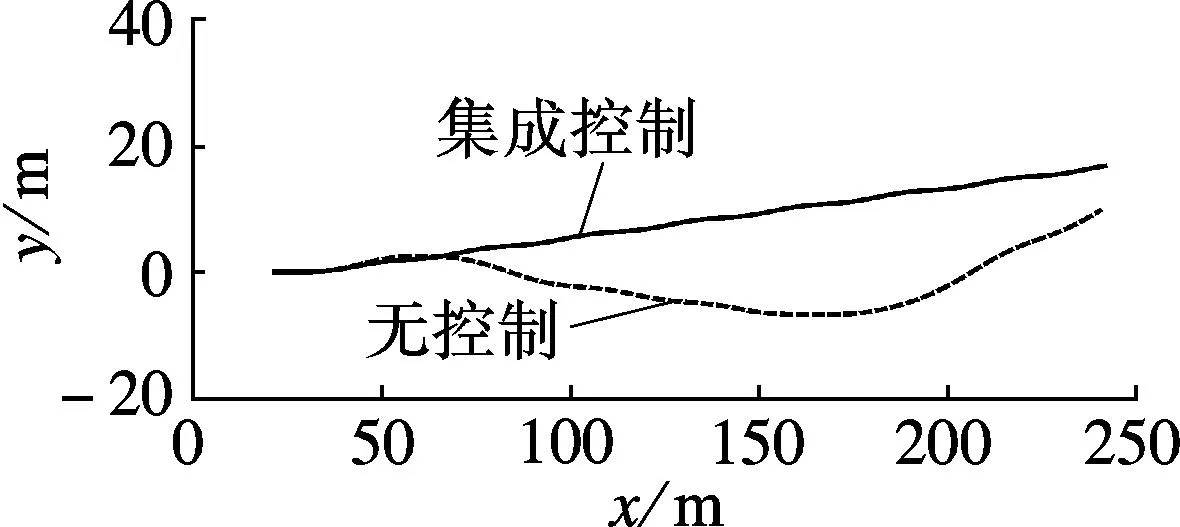
(a) 车辆轨迹

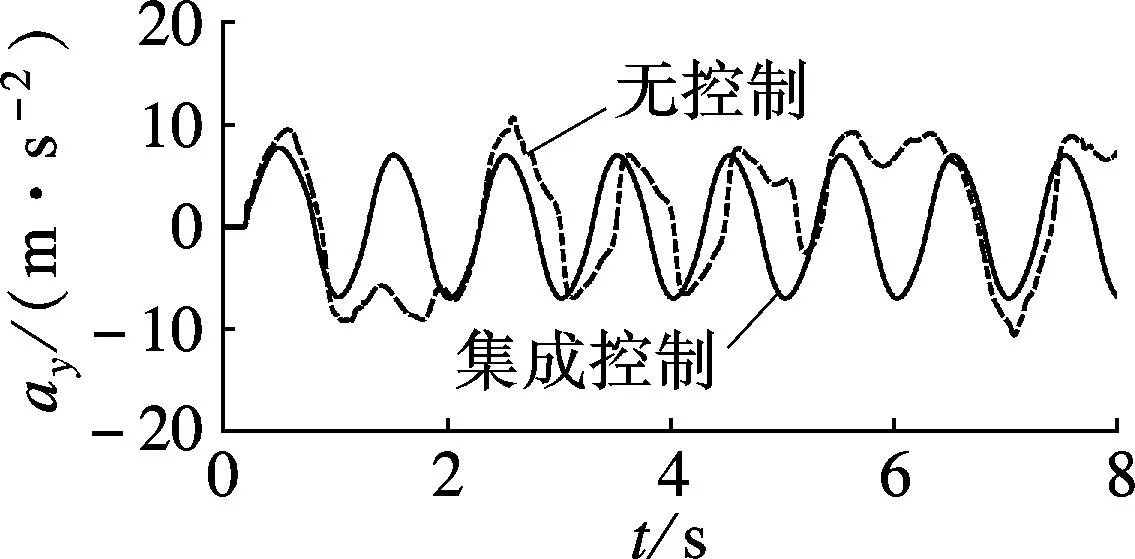
(b) 车辆侧向加速度

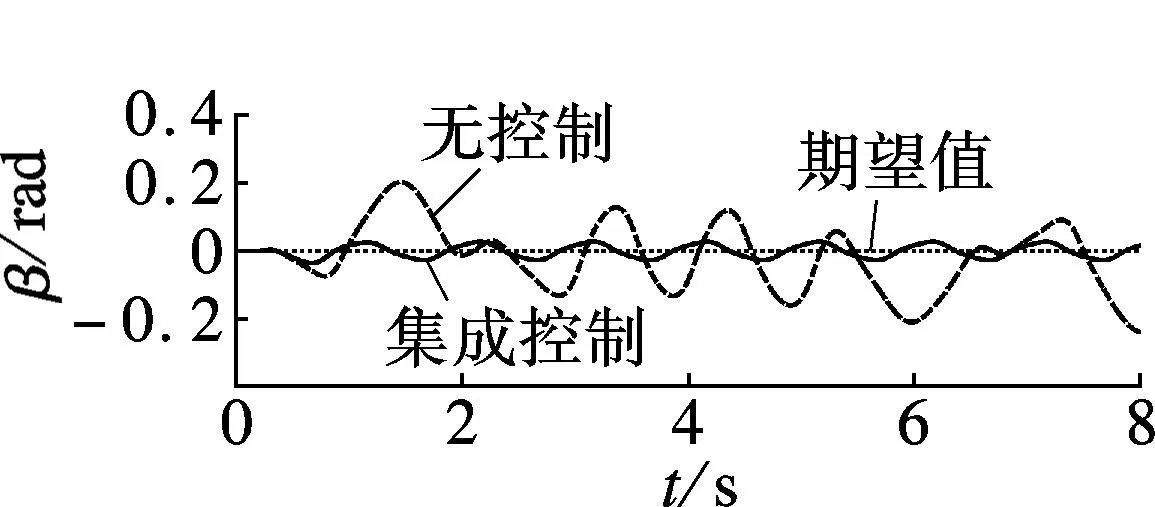
(c) 车辆质心侧偏角

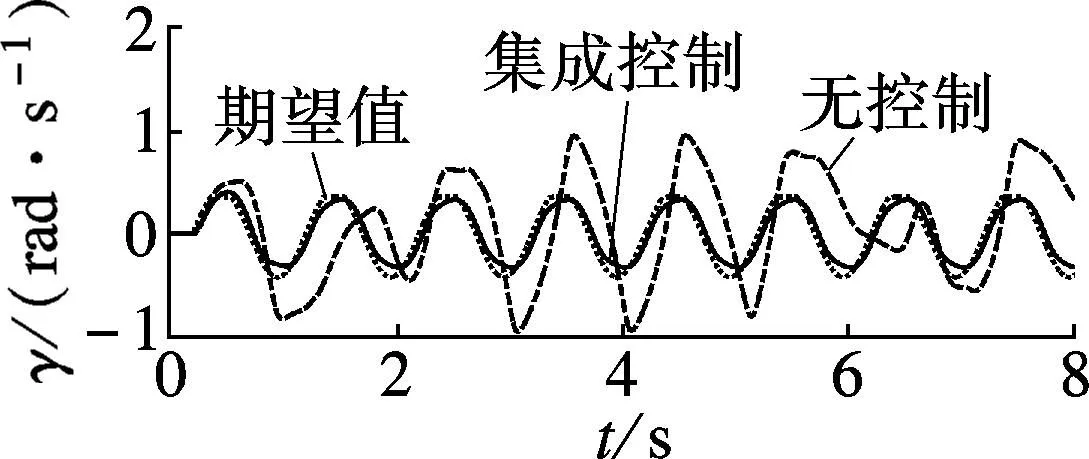
(d) 车辆横摆角速度

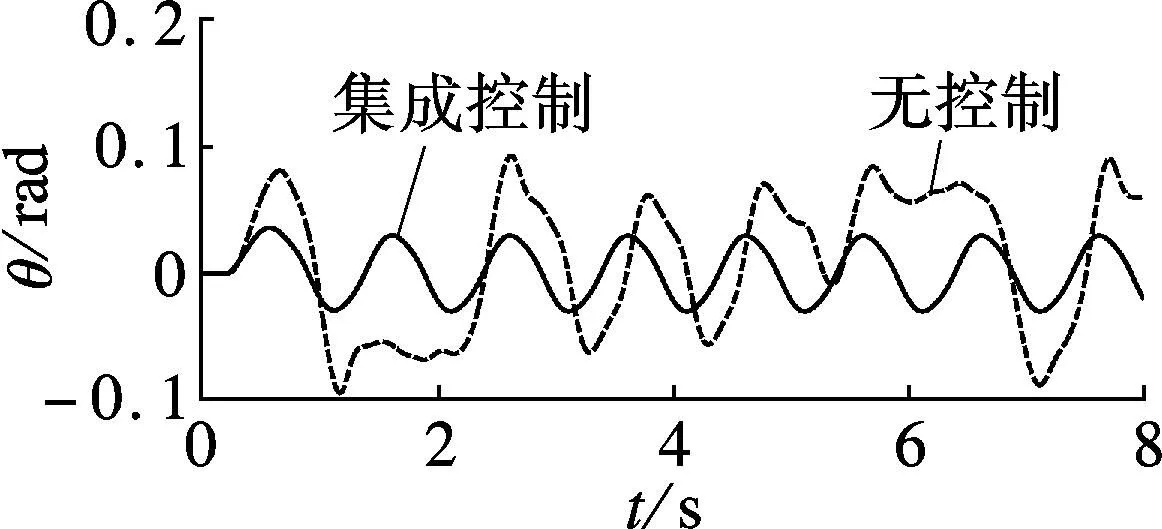
(e) 车辆侧倾角

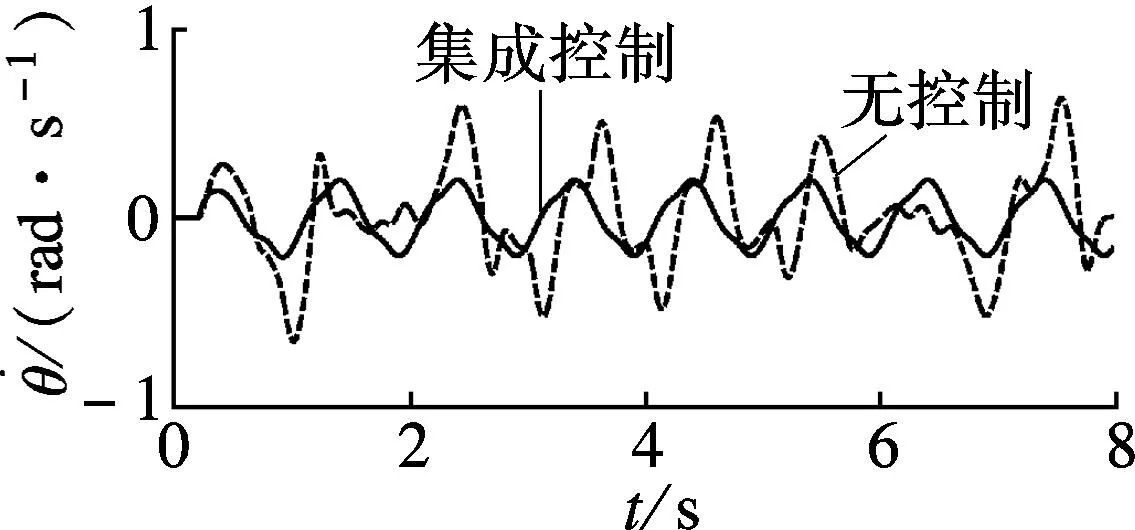
(f) 车辆侧倾角速度

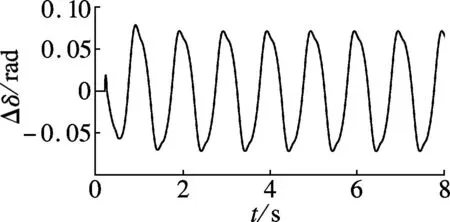
(g) 主动前轮转角

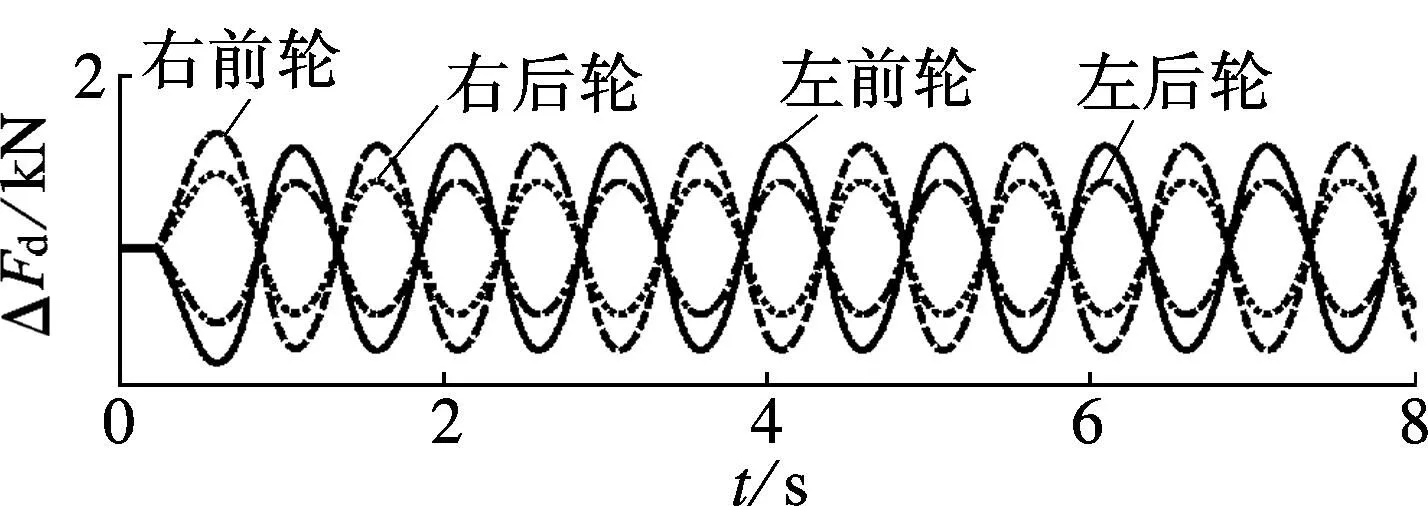
(h) 主动悬架作用力

由图3(a)～(e)可见,无控制时,车辆的质心侧偏角和横摆角速度明显偏离其期望值,并且横摆角速度响应滞后．采用底盘集成控制后,车辆横摆角速度可以较好地跟踪其期望值,并且质心侧偏角控制在较小的可控范围内．

由图3(f)、(g)可见,与采用底盘集成控制的车辆侧倾角和车辆侧倾角速度相比,无控制时,二者明显变大,车辆更易发生侧翻．

4结论

1) 基于不确定离散系统广义H2及H∞性能判据,推导出新的状态反馈广义H2/H∞控制综合方法,并将其转化为线性矩阵不等式组的凸优化问题,降低了系统保守性．

2) 考虑车辆前、后轴侧偏刚度参数的不确定性和系统多种约束条件,基于新的状态反馈广义H2/H∞控制综合方法设计车辆底盘控制器,协调控制主动前轮转向系统和主动悬架系统．

3) 典型工况仿真证明了所设计的车辆底盘集成鲁棒H2/H∞控制器能够明显地改善车辆的行驶稳定性和防侧翻能力．

参考文献(References)

[1]Cho W, Choi J, Kim C, et al. Unified chassis control for the improvement of agility, maneuverability, and lateral stability[J].IEEETransactionsonVehicularTechnology, 2012, 61(3): 1008-1020.

[2]Chang S, Lee B, Park Y, et al. Integrated chassis control for improving on-center handling behavior[J].SAEInternationalJournalofPassengerCars, 2014, 7(3):1002-1008.

[3]Zhu B, Chen Y, Zhao J. Integrated chassis control of active front steering and yaw stability control based on improved inverse nyquist array method[J].TheScientificWorldJournal, 2014: 919847-01-919847-14.

[4]Song J. Development and comparison of integrated dynamics control systems with fuzzy logic control and sliding mode control[J].JournalofMechanicalScienceandTechnology, 2013, 27(6): 1853-1861.

[5]Roshanbin A, Naraghi M. Adjustable robustness method for fuzzy logic integrated control of active steer angle and direct yaw moment[J].InternationalJournalofControlandAutomation, 2013, 6(4): 329-346.

[6]Yang X J, Wang Z C, Peng W L. Coordinated control of AFS and DYC for vehicle handling and stability based on optimal guaranteed cost theory[J].VehicleSystemDynamics, 2009, 47(1): 57-79.

[7]Yim S, Park Y, Yi K. Design of active suspension and electronic stability program for rollover prevention[J].InternationalJournalofAutomotiveTechnology, 2010, 11(2): 147-153.

[8]Yoon S H, Jung J H, Koo B K, et al. Development of rollover prevention system using unified chassis control of ESP and CDC systems[J].SAETechnicalPaperSeries, 2006, 2006-01-1276.

[9]俞立. 鲁棒控制:线性矩阵不等式处理方法[M]. 北京: 清华大学出版社, 2002: 91-96.

[10]高会军, 王常虹. 不确定离散系统的鲁棒L2-L∞及H∞滤波新方法[J]. 中国科学, 2003, 33(8): 695-706.

Gao Huijun, Wang Changhong. New approach to robust L2-L∞and H∞filter design for uncertain discrete-time systems[J].ScienceinChina, 2003, 33(8): 695-706. (in Chinese)

[11]郭孔辉. 汽车操纵动力学原理[M]. 南京: 江苏科学技术出版社, 2011: 172-179.

[12]van Zanten A T. Bosch ESP systems: 5 years of experience[J].SAETechnicalPaperSeries, 2000, 2000-01-1633.

[13]Richier M, Lenain R, Thuilot B, et al. Rollover prevention system dedicated to ATVs on natural ground[J].AppliedMechanicsandMaterials, 2012, 162: 505-514.

[14]范宣华, 陈璞, 慕文品. 结构动力方程的2种精细时程积分[J]. 西南交通大学学报, 2012, 47(1): 109-114.

Fan Xuanhua, Chen Pu, Mu Wenpin. Two precise time-integration methods for structural dynamic analysis[J].JournalofSouthwestJiaotongUniversity, 2012, 47(1): 109-114. (in Chinese)

[15]National Highway Traffic Safety Administration. A comprehensive experimental examination of test maneuvers that may induce on-road, untripped, light vehicle rollover: phase IV of NHTSA’s light vehicle rollover research program[R]. Washington, USA: National Highway Traffic Safety Administration, 2002.