修正双线性模型对隔震结构地震响应影响的研究

金建敏，谭 平，周福霖，朱 健，黄襄云，庄学真

（1. 广州大学工程抗震研究中心，广东 广州 510405； 2. 宁夏大学土木与水利工程学院，宁夏 银川 750021）

橡胶隔震支座一般分为天然橡胶支座、铅芯橡胶支座、高阻尼橡胶支座、锡芯橡胶支座等四种。隔震层可采用铅芯橡胶支座+天然橡胶支座、高阻尼橡胶支座、天然橡胶支座+黏滞阻尼器（或铅阻尼器）、或以上几种隔震装置的混合应用。铅芯橡胶支座(LRB)是目前在隔震建筑中采用最为广泛的隔震装置，它使隔震支座和阻尼器的功能一体化，可以单独在隔震系统中使用，而无需另设阻尼器，使隔震系统的组成变得比较简单[1]。在隔震计算分析中，国内通常采用不考虑剪应变相关性的微分型模型（Bouc-Wen模型）或双线性模型模拟铅芯橡胶支座[2-6]，而国外通常采用考虑剪应变相关性的修正双线性模型[7]或修正BRO模型（修正双线性+RO模型）[8]，因此有必要研究考虑铅芯橡胶支座剪应变相关性对隔震结构地震响应的影响．

1 铅芯橡胶支座修正双线性模型

铅芯橡胶支座的双线性模型，可表达为[9]：屈服前阶段（弹性阶段）

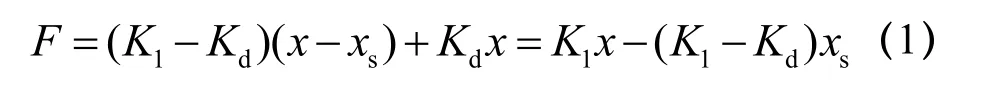
屈服后阶段

式（1）、式（2）中的力学性能指标均由铅芯橡胶支座剪切应变为100 %时压剪试验确定，实际上，剪应变相关性是不宜忽略的；为考虑铅芯橡胶支座刚度及屈服力的剪应变相关性，日本 Oiles公司基于铅芯橡胶支座的力学性能试验，提出采用修正双线型模型（图 1）对屈服前、后刚度及屈服力进行了修正，剪应变相关式见式(3)、式(4)：

式中，γ为剪切应变，等于支座水平剪切位移x与内部橡胶总厚Tr的比值。CKd(γ)、CQd(γ)分别为实测的屈服后刚度及屈服力的修正系数；分别为修正后屈服后刚度及屈服力；Kd100、Qd100分别为100 %剪应变时的屈服后刚度及屈服力；K1(γ)为修正后屈服前刚度；α为屈服后刚度与屈服前刚度的比值。采用该修正公式后屈服后刚度在γ小于及大于100 %时将分别大于及小于Kd100，而屈服力在γ小于50 %时将小于Qd100；修正双线性模型以式（5）为骨架曲线：

图1 修正双线性模型Fig. 1 Modified bilinear model

图1中1为初始弹性段（－xe＜x＜xe），按下式确定初始弹性刚度（初始屈服前刚度）：

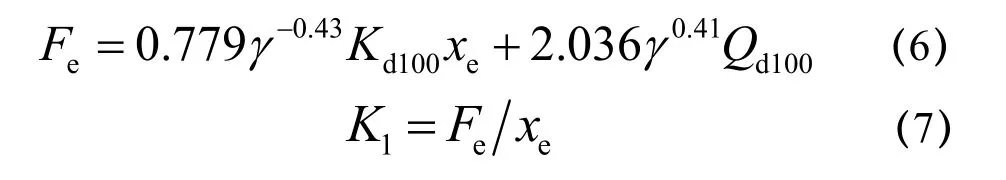
式中：xe为屈服位移，Fe为屈服位移对应的水平恢复力；2、3为沿骨架曲线移动； 4、5为卸载段；6、7为屈服后阶段．

2 剪应变相关性试验值与剪应变相关式对比

为验证剪应变相关式（3）及式（4）的正确性，分别对直径为700 mm、1 000 mm、1 100 mm的铅芯橡胶支座进行了竖向压应力15 MPa，剪切应变γ=±50 %、±100 %、±150 %、±200 %、±250 %的压剪试验。所选用的支座为隔震工程中常用的G4(剪切模量0.392 MPa)、第2形状系数S2=5系列，隔震支座参数(γ=±100 %）见表1．

表1 隔震支座参数(γ=±100 %)Tab.1 Data for LRB(γ =±100 %)

实测的屈服后刚度Kd及屈服力Qd以第3圈滞回曲线为准，不同剪切应变γ的测试结果以γ=±100 %时的测试结果为基准值进行归一化，并与剪应变相关式进行了对比，对比结果见图2及图3。从对比结果可见，试验结果与剪应变相关式吻合较好，可采用式（3）及式（4）对不同剪切应变γ的屈服后刚度Kd及屈服力Qd进行剪应变相关性修正。图4为采用修正双线性恢复力模型的LRB1 000滞回曲线．

图2 屈服后刚度Kd的剪应变相关性Fig. 2 Shear strain dependency of post yielding stiffness

图3 屈服力Qd的剪应变相关性Fig. 3 Shear strain dependency of post yielding load

图4 修正双线性恢复力模型（LRB1 000）Fig. 4 Modified bilinear restoring force model（LRB1 000）

图5 输入地震波加速度反应谱与规范反应谱对比Fig. 5 Comparison of earthquake response spectrum

3 隔震结构地震响应影响分析

为探讨修正双线性恢复力模型对隔震结构地震响应的影响，分别采用双线性模型与修正双线性恢复力模型来模拟铅芯橡胶支座，对单质点隔震结构模型、多质点隔震结构模型进行了地震响应分析。隔震层参数选用前节铅芯橡胶支座同系列LRB800（S1=33.3，S2=5.1，内部橡胶总厚为 156 mm）支座的参数（γ=±100 %），屈服后刚度、屈服力及等效阻尼比分别为 1.268 kN/mm、140.9 kN及24.9 %，屈服前刚度取为屈服后刚度的13倍；上部结构的总质量为512.91 t（按支座压应力10 MPa确定），屈重比为2.80 %。输入地震波选用El Centro-NS波、Taft-EW及一条与规范[10]反应谱吻合的人工波，图5为输入地震波的加速度反应谱与规范反应谱（8度罕遇地震，Tg=0.4 s）的对比．

3.1 单质点隔震结构模型

单质点隔震结构模型的隔震后屈服后周期为 4 s，对其进行地震响应分析，地震波加速度峰值从0.05 g至0.70 g以0.05 g为间隔逐步增加。图6、图7为不同地震波加速度峰值时双线性模型与修正双线性模型的隔震层位移比及隔震层剪力比，其中人工波输入加速度峰值达到0.45 g以后，两种双线性模型的隔震层位移均达到 2.82Tr(0.55倍支座直径)以上，超过规范限值[10]，后面的计算结果未给出。为对比两种双线性模型在铅芯橡胶支座不同剪切应变时的差异，将图6、图7中的横坐标改为双线性模型对应于不同地震波加速度峰值的铅芯橡胶支座剪切应变，可得到图8和图9．

从图6、图7可见，当地震波加速度峰值不大于0.2g时，与修正双线性模型相比，双线性模型因未考虑剪应变相关性造成的误差较大，隔震层位移的误差超过20 %，隔震层剪力的误差超过10 %；当地震波加速度峰值大于0.2 g时，隔震层位移的误差基本减小至20 %以内，隔震层剪力的误差基本减小至10 %以内；当地震波加速度峰值大于0.3 g以后，隔震层位移的误差也减小至10 %以内。从图8、图9可见，铅芯橡胶支座剪切应变在50 %以下时，双线性模型误差较大；当双线性模型计算的铅芯橡胶支座剪切应变大于50 %时，隔震层位移的误差基本在20 %以内，隔震层剪力的误差基本在10 %以内；当双线性模型计算的铅芯橡胶支座剪切应变大于100 %时，隔震层位移的误差基本在10 %以内，且双线性模型计算得到的隔震层剪力偏大。双线性模型的误差主要发生在地震波加速度峰值不大于0.2 g或铅芯橡胶支座剪切应变在50 %以下时．

3.2 多质点隔震结构模型

图6 隔震层位移比（单质点，不同加速度）Fig. 6 Displacement ratio of isolation layer(single-particle,different acceleration)

图7 隔震层剪力比（单质点，不同加速度）Fig. 7 Shear force ratio of isolation layer(single-particle,different acceleration)

图8 隔震层位移比（单质点，不同剪切应变）Fig. 8 Displacement ratio of isolation layer(single-particle, different shear strain)

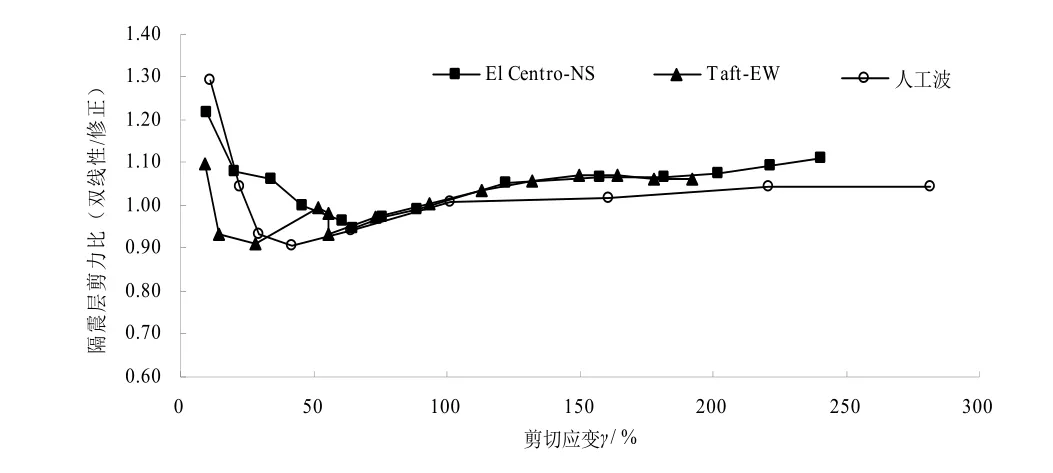
图9 隔震层剪力比（单质点，不同剪切应变）Fig. 9 Shear force ratio of isolation layer(single-particle, different shear strain)

为弥补单质点隔震模型简化的不足及研究修正双线性模型对上部结构地震响应的影响，建立上部结构总质量与单质点隔震结构模型相同的多质点隔震结构模型，上部结构为10层(层高3m，弹性层间位移角限值按钢筋混凝土结构取为1/550[10])，上部结构底层水平刚度为99.01 kN/mm，顶层水平刚度为底层水平刚度的0.5倍，中间各层的水平刚度按梯形分布插值分布，隔震前周期为1 s；隔震层参数及地震波输入工况同单质点隔震结构模型，多质点隔震结构模型的隔震后屈服后周期为4.09 s．

图10、图11、图14及图15分别为不同地震波加速度峰值时双线性模型与修正双线性模型的隔震层位移比、隔震层剪力比、上部结构层剪力比及层倾覆弯矩比，其中人工波输入加速度峰值达到0.45 g以后，两种双线性模型的隔震层位移均达到2.86Tr(0.56倍支座直径)以上，超过规范限值[10]，后面的计算结果未给出。将图10、图11、图14及图 15中的横坐标改为对应的铅芯橡胶支座剪切应变（双线性模型），得到图12、图13、图16及图17；分别为不同剪切应变时（双线性模型），双线性模型与修正双线性模型的隔震层位移比、隔震层剪力比、上部结构层剪力比及层倾覆弯矩比。图14-17中上部结构层剪力比及层倾覆弯矩比，给出了各层比值中的最大值及最小值．

由图10-13可见，当地震波加速度峰值不大于0.2 g或铅芯橡胶支座剪切应变在50 %以下时，双线性模型因未考虑剪应变相关性造成的误差较大，隔震层位移的误差超过20 %，隔震层剪力的误差超过10 %；当地震波加速度峰值大于0.2 g或双线性模型计算的铅芯橡胶支座剪切应变大于50 %时，隔震层位移的误差基本减小至20 %以内，隔震层剪力的误差基本减小至10 %以内；当地震波加速度峰值大于0.4 g或双线性模型计算的铅芯橡胶支座剪切应变大于100 %时，隔震层位移的误差也基本减小至10 %以内，且双线性模型计算得到的隔震层剪力偏大。铅芯橡胶支座采用不考虑变形相关性的双线性模型，多质点与单质点隔震结构模型的隔震层地震响应误差范围基本一致．

由图14-17可见，双线性模型上部结构各层层剪力及层倾覆弯矩的误差主要发生在地震波加速度峰值不大于 0.2 g或铅芯橡胶支座剪切应变在50 %以下时．当地震波加速度峰值大于0.2 g以上或铅芯橡胶支座剪切应变在50 %以上时，上部结构各层层剪力及层倾覆弯矩的误差基本减小至 20 %以内；随着地震波加速度峰值或铅芯橡胶支座剪切应变增大，由各层层剪力及层倾覆弯矩比值最大值及最小值形成的包络范围有减小的趋势．

表2给出了各地震波输入，层间位移角小于1/550的最后一个工况及输入加速度峰值最大的工况时的上部结构层间位移角，Taft EW波各工况层间位移角均小于1/550，只列出输入峰值0.7 g时的结果，可见上部结构基本处于弹性．

图10 隔震层位移比(多质点，不同加速度)Fig. 10 Displacement ratio of isolation layer(multi-particle, different acceleration)

图11 隔震层剪力比(多质点，不同加速度)Fig. 11 Shear force ratio of isolation layer(multi-particle, different acceleration)

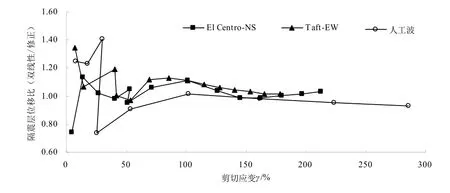
图12 隔震层位移比(多质点，不同剪切应变)Fig. 12 Displacement ratio of isolation layer(multi-particle, different shear strain)

图13 隔震层剪力比(多质点，不同剪切应变)Fig. 13 Shear force ratio of isolation layer(multi-particle, different shear strain)

图14 层剪力比(多质点，不同加速度)Fig. 14 Story shear ratio(multi-particle, different acceleration)

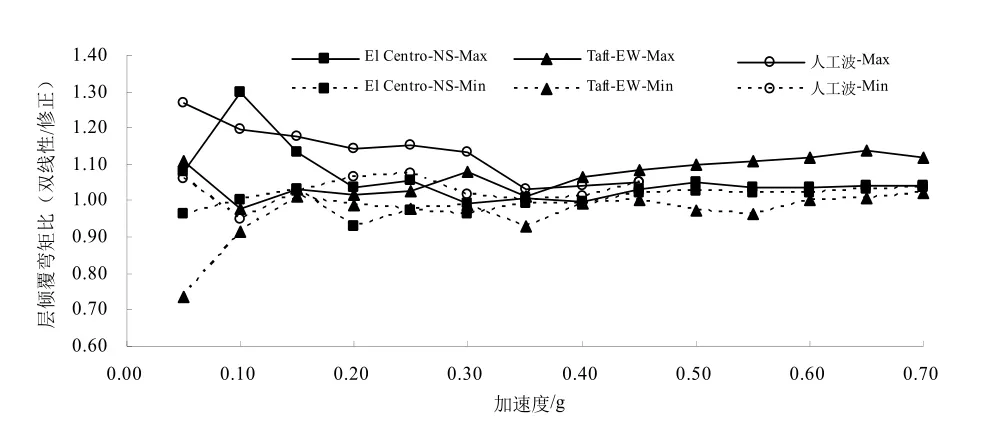
图15 层倾覆弯矩比(多质点，不同加速度)Fig. 15 Story overturning moment ratio(multi-particle,different acceleration)

图16 层剪力比(多质点，不同剪切应变)Fig. 16 Story shear ratio(multi-particle,different shear strain)

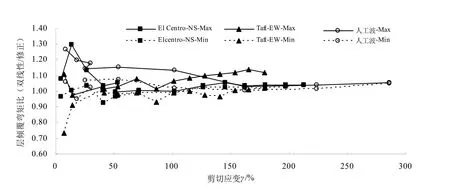
图17 层倾覆弯矩比(多质点，不同剪切应变)Fig. 17 Story overturning moment ratio(multi-particle,different shear strain)

表2 层间位移角Tab.2 Story drift

4 结论

研究了铅芯橡胶支座的修正双线性恢复力模型及其对隔震结构地震响应的影响，结论如下：

（1） 通过对直径为 700 mm、1 000 mm、1 100 mm的铅芯橡胶支座进行的剪应变相关性试验，验证了屈服后刚度Kd及屈服力Qd的剪应变相

关性修正公式，使用该公式的修正双线性模型，可用来模拟铅芯橡胶支座．

本文隔震结构模型的计算结果表明：当地震波加速度峰值不大于0.2 g或或铅芯橡胶支座剪切应变在50 %以下时，与修正双线性模型相比，双线性模型因未考虑剪应变相关性造成的误差较大；当地震波加速度峰值大于0.2 g或铅芯橡胶支座剪切应变在50 %以上时，隔震层及上部结构的地震响应的误差基本在20 %以内．

综上可见，不考虑剪应变相关性的双线性模型基本能够满足要求，但需注意到地震波加速度峰值或铅芯橡胶支座剪切应变较小时的较大误差．

References

[1]周福霖. 工程结构减震控制[M]. 北京：地震出版社,1997.ZHOU Fulin. Seismic control of structures[M]. Beijing：Seismological Press, 1997.

[2]BOUC R. Forced vibration of mechanical system with hysteresis [C]//Proceeding of 4th conference on nonlinear oscillation, Czechoslovakia, Prague ,1967.

[3]PARK Y J, WEN Y K , ANG A H-S. Random vibration of hysteretic systems under bi-directional ground motions[J].Earthquake Engineering and Structural Dynamics,1986(14):543-557.

[4]中国建筑标准设计研究院.SAP2000中文版使用指南[M]. 北京：人民交通出版社,2006.China Institute of Building Standards Dsign & Research..Guide of SAP2000-Chinese version[M]. Beijing：People′s Communication Press,2006.

[5]中国建筑标准设计研究院.ETABS中文版使用指南[M].北京：中国建筑工业出版社,2004.China Institute of Building Standards Dsign & Research..Guide of ETABS Chinese version[M]. Beijing：China Architecture & Building Press,2004.

[6]马长飞，谭平，张亚辉，等. 考虑P–△效应的柱顶隔震结构的动力响应分析[J].土木工程学报，2010,43(S):230-234.MA Changfei, TAN Ping, ZHANG Yahui et al. Dynamic responses analysis of structures with isolators on the top of the columns consideringP–△effects[J].China Civil Engineering Journal, 2010,43(S):230-234.

[7]日本建筑协会. 隔震结构设计[M]. 刘文光，译．北京：地震出版社，2006.Japanese Architecture Institute. Recommendation for design of base isolated building[M]. LIU Wenguang,Translated . Beijing：Seismological Press,2006.

[8]FENG Demin, MIYAMA Takafumi, TORII Tsugio et al. A new analytical model for the lead rubber bearing[C]//12WCEE, New Zealand: Auckland, 2000.

[9]SKINNER R I, ROBINSON W H , MCVERRY G H. An introduction to seismic isolation[M].NewYork: John Wiley&Sons, 1993.

[10]GB50011-2010 建筑抗震设计规范[S].北京: 中国建筑工业出版社, 2010.GB50011-2010,Code for seismic design of buildings[S]．Beijing：Building Industry Press of China，2010.