基于改进遗传算法的自由曲面重建及数控加工*
赵艺兵,温秀兰,张中辉
(南京工程学院 a.工业中心;b.自动化学院,南京 211167)
基于改进遗传算法的自由曲面重建及数控加工*
赵艺兵a,温秀兰b,张中辉b
(南京工程学院 a.工业中心;b.自动化学院,南京211167)
摘要:提出了用B样条表示自由曲面,基于改进遗传算法(IGA)重建自由曲面,其中节点矢量由IGA优化得到,控制顶点坐标由最小二乘法根据数据点参数值及由IGA优化得到的节点矢量计算得到。改进遗传算法采用实数编码,选择最小代沟模型和混合交叉策略,算法简单,鲁棒性强。通过对自由曲面零件在坐标测量机实测得到数据采用提出的方法重建曲面并生成CAD模型,根据CAD模型图详细分析了零件加工工艺,完成了自由曲面零件的仿真切削与数控加工,经三坐标测量仪对零件实测并计算自由曲面的轮廓度误差验证了曲面重建及加工方法的正确性、合理性。
关键词:自由曲面;B样条;改进遗传算法;数控加工
0引言
自由曲面零件在汽车、飞机、涡轮叶片、直升机螺旋浆等零件中广泛应用,已有学者提出了有关自由曲面建模和加工方法[1-2],但多数研究集中在自由曲线曲面的数学表示。数学模型未知的自由曲面建模和制造对于逆向工程至关重要,逆向工程中主要问题之一是根据已有零件生成模型或表示模型,再由已生成的模型加工零件。对于简单几何形体,由图形生成零件并非很困难,但是对于复杂零件曲面重建是有难度的。为此,近年来,许多研究者致力于自由曲面重建,Gu 和 Yan[3]提出了使用四层神经网络根据已有自由曲面重建其CAD模型,Lin[4]提出采用诱导神经网络方法建立表面参数方程,Adi[5]等提出使用粒子群优化算法求解曲线逼近问题,Akemi[6]等使用迭代两间断遗传算法重建多项式B样条曲面。但是,上述方法的实验结果多是建立在对仿真模型的验证上,并未对实际自由曲面进行测量和重建。本文以沐浴露瓶实物为例,在三坐标测量机上测量该零件,使用提出的方法重建该零件并生成CAD模型,以此为基础,进行自由曲面零件的仿真加工和数控加工,给出了详细的加工工艺。
1自由曲面表示
1.1基于B样条的自由曲面表示
B样条是具有最小支撑集的样条函数,在工业界中被广泛应用。给定控制点Pij(i=0,1…m,j=0,1,…,n)及节点矢量 U=[u0,u1,…,uM-1,uM]和V=[v0,v1,…,vN-1,vN],阶数为 (p, q)的B样条参数曲面S(u, v) 可表示为[7]:
(1)
其中 m+1 和 n+1 分别为沿着u 和 v 方向的控制点数目, Ni,p(u) 和 Nj,q(v) 为标准化B样条基函数。
1.2数据点参数化
数据点参数化是解决自由曲面重建的一个关键问题,假设被测自由曲面上三维数据表示为:G={Gr,s=(xr,s,yr,s,zr,s)},r=0,1,…;R,s=0,1,…,S,使用弦长参数法表示:
(2)

1.3节点矢量
采用非周期节点矢量重建曲面,节点矢量U和V为非减序列,可表示为:
U=[u0,u1,…,up,up+1,up+2…uM-p-1,uM-p,…,uM]=
[a,a,…,a,up+1,up+2…uM-p-1,b,b,…,b]
(3)
V=[v0,v1,…,vq,vq+1,vq+2…vN-q-1,vN-q,…,vN]=
[a,a,…,a,vq+1,vq+2…vN-q-1,b,b,…,b]
(4)
通常 a取值为 0, b 取值为1,(up+1,up+2…uM-p-1),(vq+1,vq+2…vN-q-1) 称作内节点矢量,本文采用改进遗传算法对内节点矢量进行优化。
1.4控制点计算
被测自由曲面上的三维控制点G={Gr,s=(xr,s,yr,s,zr,s)}由B样条曲面表示为:
∀r=0,…,R;s=0,…,S
(5)
为计算控制点, 式(5)重写为:
G=N(ur)PNT(vs)
(6)
其中

Ni,p=(Ni,p(u0),Ni,p(u1),…,Ni,p(uR))
Nj,q=(Nj,q(v0),Nj,q(v1),…,Nj,q(vS))
将式 (6) 拓展为用矩阵表示:
vec(G)=
Ε·vec(P)
(7)
其中拓展矩阵E的每一个元素Ni,p⊗N(vS) 的维数为(R+1)×(n+1),vec(G)为长度为(R+1)×(S+1) 的列矢量,vec(P)为长度为 (m+1)×(n+1)的列矢量,将式 (7) 两边同乘ET,有:
ETvec(G)=ETE·vec(P)
(8)
式(8)可重写为:
vec(P)=(ETE)-1ETvec(G)
(9)
由式(9)可见,控制点计算转换为求解经典的线性最小二乘解问题。当数据点的参数值和节点矢量已知时,B样条曲面的控制点可以通过式(9)计算得到。
2改进遗传算法实现自由曲面重建
2.1自由曲面轮廓度误差
根据GB/T1182-1996中定义,面轮廓度误差的公差带是包络一系列直径为公差值t的球的两包络面间的区域,诸球的球心位于具有理论正确尺寸的几何形状的曲面上。计算自由曲面轮廓度误差需要首先由已知离散点重建理论轮廓曲面,再计算所有测量点Ak(k=0,1,…,V, V为测点数目)到理论轮廓曲面的最小距离δk,找出最小距离δk中的最大值,则自由曲面轮廓度误差最小区域解f等于该最大值的2倍,即
f=2max(δk)
(10)
2.2自由曲面重建
自由曲面重建可看成求最小化问题,其目标函数定义为B样条上各点S(ui,vj)和被测曲面上点Gr,s欧式距离和的平均值,表示为:
(11)
由式(11) 可见,目标函数f为节点矢量的函数,因此自由曲面重建转换为搜索内节点 (up+1,up+2…uM-p-1) 和(vq+1,vq+2…vN-q-1) ,以使目标函数值 f 为最小。
本文提出用改进遗传算法(IGA)搜索式(11)的最小值,完成自由曲面重建。IGA采用实数编码,选择最小代沟模型和混合交叉策略[8],算法流程如下:
(1)随机产生N个种群;
(2)从种群中任意选取两个个体X1,X2作为父代;
(3)将两个父代个体X1,X2重复使用BLX-α交叉产生nc个子代个体;

(12)
式(12)中,xi1,xi2分别为父代个体X1,X2的第i个基因值,α是一个正数,一般取α=0.5。
(4)从父代X1,X2和nc个子代个体中选择目标值最小的两个个体替换原来的两个父代X1,X2;
(5)判断是否满足终止条件,若不满足,则转(2)。
使用IGA实现自由曲面重建的流程如图1所示。

图1 改进遗传算法实现自由曲面重建流程图
3自由曲面工艺设计及仿真切削
以沐浴露瓶重建加工为例,首先使用三坐标测量机测量沐浴露瓶得到一系列测量点,由提出方法重建该瓶并运用MasterCam软件完成其CAD图绘制,见图2,然后进行仿真加工。

图2 重建的自由曲面CAD图
3.1工艺方案及加工工艺
(1) 毛坯:材质为LY12(硬铝),已加工过的方料265×145×80mm。
(2) 工序步骤:
外形挖槽加工:该零件采用铝材加工,由于周边余量较大,所以用挖槽加工方法去除加工余量。挖槽加工时,切削深度分层铣削,最大切削深度2mm,精加工余量0.5mm,切削方式选择等距环切。
凹槽加工:凹槽加工选择挖槽加工方式,切削深度分层铣削,最大切削深度2mm,精加工余量0.5mm,切削方式选择等距环切。
曲面粗加工:粗加工时采用平行铣削的方式,最大切削间距1.5mm,预留0.5mm的余量进行精加工,为了缩短切削时间,切削方式选择双向切削。
曲面精加工:为了保证零件表面粗糙度,精加工最大切削间距设为0.1mm,切削方式单向切削。
3.2刀具选择
由于材料较软,选常用的高速钢铣刀,允许切削速度就很高。分粗精加工,从切削性能和加工的表面粗糙度情况考虑,挖槽选用φ8的平头立铣刀,曲面粗加工选用φ8的球头铣刀,曲面精加工选用φ5的球头铣刀。
确定切削用量:用查表法确定主轴转速和进给速度。
查表可知,铝合金允许切削速度为180~360m/min,取V=180m/min。粗加工V=180m/min×70%=126m/min;φ8粗加工时每齿切削量取Sz=0.06mm/齿。φ5精加工时每齿切削量取Sz=0.05(mm/齿)/2=0.025mm/齿。考虑到机床刚性因素,乘以修正系数0.6。
当选用φ8立铣刀时,n=1000V/πD=(1000×126×0.6)/(3.14×8)≈3010r/min
F=2Szn=2×0.06×3010=361mm/min
当选用φ5立铣刀时,n=1000V/πD=(1000×180×0.6)/(3.14×5)≈6879r/min
F=2Szn=2×0.025×6879=344mm/min
经过计算和结合实践经验,得出切削用量加工工序卡见表1所示。
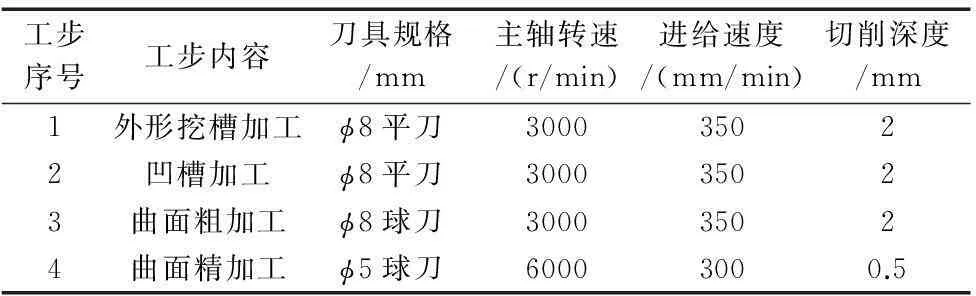
表1 沐浴露瓶的加工工序卡
3.2仿真切削
运用MasterCam软件进行仿真切削。该零件的仿真切削加工主要包括瓶身外形挖槽加工、瓶身凹槽加工、曲面粗加工及曲面精加工几部分。每一部分加工均需进行工件参数设定、刀具参数设置、仿真加工。以瓶身外形挖槽加工为例,工件参数设定及刀具参数设置分别如图3、图4所示,经挖槽参数设定、粗铣/精修参数设置后,生成刀具路径,完成仿真加工如图5所示。再经瓶身凹槽加工、曲面粗加工及曲面精加工,得到的曲面精加工仿真结果如图6所示。

图4 刀具参数设置

图3 工件参数设定

图5 外形挖槽仿真切削结果

图6 曲面精加工仿真切削结果
4自由曲面数控加工
由前面仿真加工的结果,对该自由曲面零件进行刀具路径规划[9-10],利用MasterCam的后置处理功能,生成NC数控加工程序如图7所示,在配备有NURBS曲线插补能力的SIEMENS840D数控铣床上加工该零件。

图7 NC加工程序
在数控铣床上经加工机床返回参考点、刀具参数设置、对刀操作、工件原点MDA方式校验、加工通讯后,将每步程序传输进入铣床系统后,进行外形挖槽铣削、凹槽加工、曲面粗加工平行铣削、曲面精加工平行铣削,完成了该自由曲面零件加工,其外形挖槽铣削、曲面粗加工及其实物分别如图8~图10所示。使用Miracle NC464三坐标测量机对该零件实测,由该测量机安装的美国RATIONAL-DIMS软件计算的曲面轮廓度误差为0.36mm,符合设计及加工要求,证实了所提出自由曲面重建及加工方法是合理可行的。

图8 外形挖槽铣削

图9 曲面粗加工

图10 零件成品
5结论
提出了用B样条表示自由曲面零件,用改进遗传算法优化内节点的自由曲面重建方法,与传统优化方法相比,该方法具有算法简单、优化效率高的特点。在三坐标测量机实测自由曲面零件得到数据采用改进遗传算法重建曲面,在详细分析了零件加工工艺基础上完成了刀具选择、零件的仿真切削与数控加工,将加工后的零件经坐标测量仪实测并计算该自由曲面轮廓度误差,其结果符合设计要求,证实了提出方法的正确性。该方法可进一步能够推广应用于其它自由曲面零件的加工。
[参考文献]
[1] Hsieh H T,Chu C H.Optimization of tool path planning in 5-Axis flank milling of ruled surfaces with improved PSO [J].International Journal of Precision Engineering and Manufacturing 2012,13(1):77-84.
[2] 耿生玲,康宝生.基于SOFM与RBF神经网络的自由曲面重建[J].计算机工程与设计,2007,28(12):65-68.
[3] Gu P,Yan X.Neural network approach to the reconstruction of free form surfaces for reverse engineering[J].Computer-Aided Design,1995, 27(1):59-69.
[4] Lin J C. Free-form surface rebuild using an abductive neural network[J].Journal of Materials Processing Technology, 2001, 116:170-175.
[5] Adi D I S, Shamsuddin S M B, Hashim S Z M. NURBS Curve Approximation using Particle Swarm Optimization[J].Seventh International Conference on Computer Graphics, Imaging and Visualization. Sydney: CGIV, 2010:73-79.
[6] Akemi G, Andrés I,Jaime P P.Iterative two-step genetic-algorithm-based method for efficient polynomial B-spline surface reconstruction[J]. Information Sciences,2012,182(1):56-76.
[7] 朱心雄.自由曲线曲面造型技术[M].北京:科学出版社,2000.
[8] 温秀兰,王东霞,盛党红,等.改进遗传算法用于自由曲线重建研究[J].中国机械工程,2012,23(17): 2048-2052.
[9] 张小明,王清辉,王帅.基于曲面凹凸特征的环切加工轨迹生成方法[J].组合机床与自动化加工技术,2014(3):134-136.
[10] 陈英俊,陈小童.MasterCAM在复杂曲面数控铣削加工中的应用研究[J].组合机床与自动化加工技术,2013(4):96-98.
(编辑赵蓉)
Free-form Surface Reconstruction Based on Improved Genetic Algorithm
and its Numerical Control Machining
ZHAO Yi-binga,WEN Xiu-lanb,ZHANG Zhong-huib
(a.Industry Center;b.Automation Department, Nanjing Institute of Technology, Nanjing 211167, China)
Abstract:B-spline is used to express free-form surface parts and an improved genetic algorithm (IGA) is proposed to reconstruct free-form surface, where knot vectors are optimized by IGA and the coordinates of control points are calculated by the least square method according to the parameter values of data points and knot vectors optimized by IGA. IGA is based on real-coded and the minimum generation gap model and mix cross strategy are used. It has the advantages of simple algorithm and strong robustness. An actual surface was reconstructed based on the data of an actual free-form parts measured on coordinate measurement machine. Based the CAD model of the parts, the process technology is analyzed explicitly and the stimulation cutting and numerical control machining of the free-form parts are finished. The surface profile error is calculated by measuring the finished parts on CMM and it verifies that the design and machining methods are correct and reasonable.
Key words:freeform surface; B-spline;an improved genetic algorithm; numerical control machining
中图分类号:TH166;TG65
文献标识码:A
作者简介:赵艺兵(1966—),男,呼和浩特人,南京工程学院高级实验师,研究方向为数控技术、逆向工程、精密检测,(E-mail)zdhxzyb@njit.edu.cn。
*基金项目:国家自然科学基金项目(51075198);江苏省333高层次人才项目资助(2014-3-45);江苏省六大人才高峰项目资助(2011-ZBZZ-032)
收稿日期:2015-03-15;修回日期:2015-03-31
文章编号:1001-2265(2015)12-0109-04
DOI:10.13462/j.cnki.mmtamt.2015.12.029

