基于响应面模型的引线键合混合模式轨迹规划*

黄运榜，赵翼翔，陈　新

(广东工业大学 广东省计算机集成制造系统重点实验室，广州　510006)



基于响应面模型的引线键合混合模式轨迹规划*

黄运榜，赵翼翔，陈新

(广东工业大学 广东省计算机集成制造系统重点实验室，广州510006)

摘要：以焊线机劈刀为研究对象，以劈刀运动轨迹的跟随误差和重复误差为优化目标，选取不同控制模式作为试验变量，采用正交试验设计方法进行试验，应用正交试验数据建立轨迹的运动模式与优化目标之间的响应面模型，用多目标遗传算法获得优化目标的Pareto最优解。在焊线机试验平台上验证用响应面模型以及多目标遗传算法优化引线键合混合模式轨迹规划的准确性。结果表明，引线键合中采用混合模式轨迹规划相对于单一模式可以提高轨迹运动的精度。

关键词：响应面模型；多目标遗传算法；轨迹规划；Pareto最优解

0引言

引线键合中劈刀运动决定封装元件的电学特性和可靠性,而劈刀运动由线弧轮廓决定。通过规划劈刀运动轨迹可以得到理想的引线键合线弧轮廓。国内外学者对轨迹规划做了大量研究。针对机器人多关节合成运动采用分段规划轨迹，用多项式函数分段规划，这样可保证位置、速度、加速度连续，实现轨迹平滑、运动稳定[1-2]。采用分段规划与整段运动一起规划相比，可以减小轨迹规划过程中的计算量，同时更好的保证轨迹平滑。曹波等用样条曲线对搬运机器人的运动轨迹进行规划，在保证速度，加速度连续基础上提出基于时间最优的规划方法，对机器人整个码垛过程进行再规划[3-5]。该方法应用于搬运机器人的特定的工作方式和特定的机械结构的PTP运动模式上效果好，但基于时间优化难以满足轨迹轮廓精度要求。胥晓基于ACR9000运动控制器规划引线键合线弧，其采用S曲线加减速方法以跟随误差和稳态误差为指标规划轨迹[6],其用单一模式对整段运动整体规划，没有考虑混合模式规划。

本文将轨迹进行分段，用不同控制模式来规划每段运动，在保证位置、速度、加速度连续基础上以劈刀运动轨迹的跟随误差和重复误差为试验指标优化。在优化过程中，把不同的控制模式数值化，并结合正交试验建立不同控制模式与试验指标的数学模型，用多目标遗传算法获得优化目标的Pareto最优解，从而得到最优轨迹规划方式，实现劈刀轨迹规划。混合模式轨迹规划图，见图1。

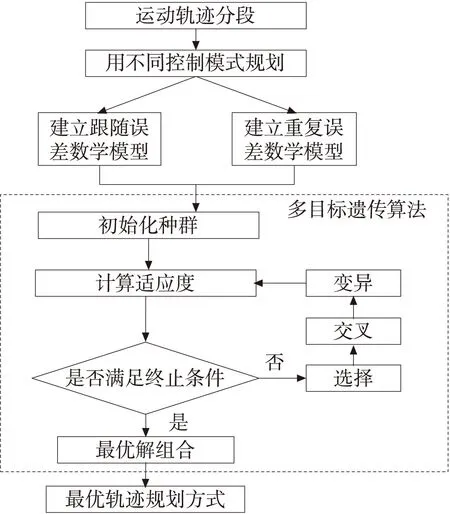
图1　混合模式轨迹规划图

1引线键合运动平台简介

本文以平面LED全自动超声波金丝球焊线机WB2001为试验平台，见图2。实验平台选用的是美国泰道的PMAC运动控制器。该控制器可通过USB接口外接 PC，可实现在线编程控制，PID参数调整，电机参数设置，实现实验数据采集等。此外，该控制器提供了多路 I/O 扩展接口，便于实现与其它电机的协调运动以及自身模式间的切换。

劈刀运动控制系统主要组成有PMAC运动控制卡、ELMO驱动器、多摩川音圈电机，光栅尺编码器。劈刀驱动电机(音圈电机)控制信号流：PMAC卡通过J3(JMACH1)串口把控制模拟制信号通过DTC-8B转接板传(起扩展、隔离保护作用)到ELMO HARMONIC伺服驱动器(ANLIN1+，ANLIN1-表示模拟信号)，伺服驱动器将模拟信号转化为电流信号给音圈电机，光栅尺测量的位置信号和标志位反馈信息给PMAC卡，形成位置闭环和速度闭环控制，另外电流环是通过电流传感器在伺服驱动器内形成闭环，见图3。音圈电机使用三环(电流，速度，位置)闭环控制，保证了劈刀运动精度。

图2　焊线机试验平台

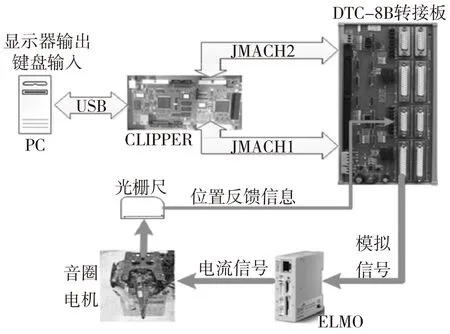
图3　音圈电机控制信号图

2响应面模型及多目标遗传算法

2.1响应面模型法

响应曲面是用来处理多个变量建模、分析问题的统计处理方法，该方法基础是实验设计，其基本理论思想是构造数学模型来表达试验因素与实验指标的数学关系。常见的响应曲面模型有一阶响应模型(线性响应模型)，

(1)

二阶响应曲面模型

(2)

其中，βn、βnn、βnq分别表示试验因素xn的一阶系数、xn的二阶系数、xn与xq之间的交互作用系数；xin、xiq分别表示xn第i次试验的取值和xq第i次试验的取值；εi表示误差项；yi表示第i组试验因素的响应值；m为试验因素总数；n为试验因素的个数(n=1,2,3，…，m)[7]。

建立响应面模型再通过最小二乘逼近方法拟合，得到数学模型。最小二乘法拟合是使拟合值与试验值的误差最小得到响应面模型的系数，如式(3)。

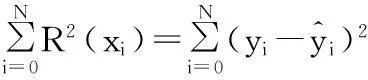
(3)

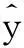
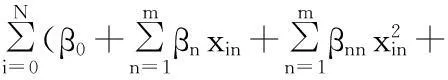
(4)

关于β求偏导，并令其为零，就可得到响应面模型的系数，从而得到数学模型。

2.2多目标遗传算法

1967年，Rosenberg在他的研究中考虑到用遗传的搜索算法求解多目标优化问题，将遗传算法思想应用到多目标优化问题中，开创了遗传算法在多目标优化应用领域中的研究。对于如何求解多目标优化问题的pareto最优解，目前已经提出了多种基于进化算法的求解方法，如并列选择法、非劣分层遗传算法、基于目标加权的遗传算法、多目标遗传算法。

遗传算法主要由4个部分组成:编码方式、适应度函数、遗传操作、算法终止条件。要利用遗传算法成功的解决优化问题,每个部分的设计都非常关键。在应用遗传算法时应设置好初始种群个数,交叉概率和变异概率这三个关键参数,其确定规则如下:

(1)群体规模：群体规模影响遗传优化的最终结果以及遗传算法的执行效率。当群体规模太小时,遗传算法的优化性能一般不会太好,而采用较大的群体规模则可减少遗传算法陷入局部最优解的机会,但较大的群体规模意味着计算复杂度高。

(2)交叉概率：交叉概率控制着交叉操作被使用的频度。较大的交叉概率可增强遗传算法开辟新的搜索区域的能力,但高性能的模式遭到破坏的可能性增大;若交叉概率太低,遗传算法搜索可能陷入迟钝状态。

(3)变异概率：变异在遗传算法中属于辅助性的搜索操作,它的主要目的是维持解群体的多样性。低频度的变异可防止群体中重要的单一基因的可能丢失,高频度的变异将使遗传算法趋于纯粹的随机搜索[8]。

3单目标响应面模型构建

根据引线键合的工艺要求，将劈刀运动轨迹分为三段的运动，并用x1、x2、x3分别表示运动过程中的第一、二、三段运动，用四种轨迹规划模式LINEAR模式、LINEAR_S模式、SPLINE模式、RAPID模式来规划各段运动轨迹，得到混合模式劈刀运动控制模式与试验指标的试验数据，见表1。

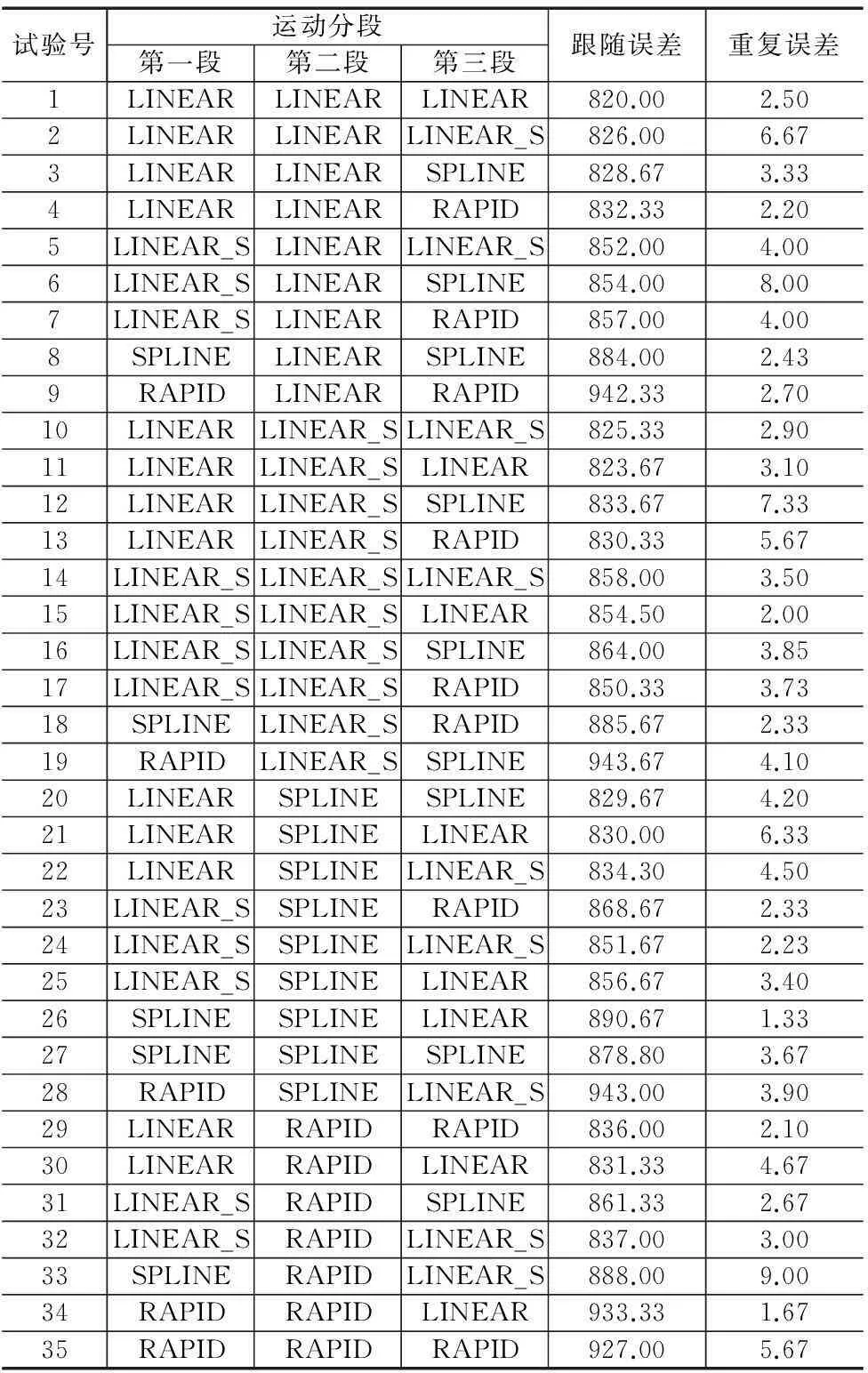
表1　混合模式试验数据统计

根据试验数据，建立数学模型进行优化计算。由于所得的跟随误差和重复误差的数值大小差别大，为了得到更精确的模型和准确的计算结果，对两个试验指标进行尺度转换。对转换值采用最小二乘法拟合二阶响应面模型，计算得响应面模型(2)的系数，如表2。

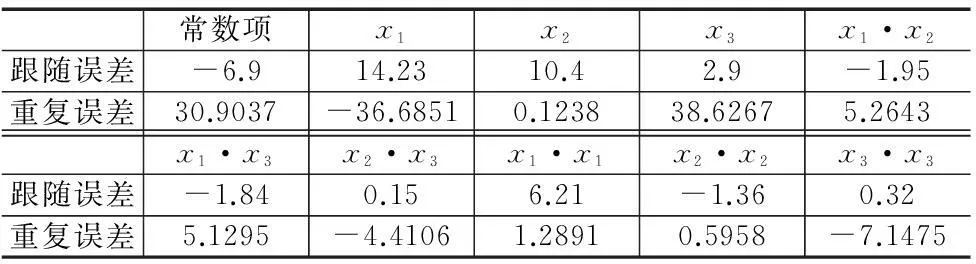
表2　响应面模型系数表

在应用响应面模型前，先对模型进行方差分析和残差分析检验。分析得到跟随误差响应曲面模型和重复误差响应曲面模型的方差和残差，见表3。

表3　试验指标模型方差分析结果

表3中，“平方和”表示建立的模型的各个系数值之和，“自由度”表示预测模型的系数个数。跟随误差模型的F值为215.258，大于F0.01、大于F0.05，说明该模型在统计学上是有意义的；重复误差的F值为2.213，大于F0.01、小于F0.05，说明该模型在统计学上是有意义的。两个模型的”P值”分别为小于0.0001和0.0351，都小于0.05，表示这两模型的系数是有意义的。综合分析可知，所建立试验指标的响应曲面模型是有效的。

根据跟随误差模型系数表可得其目标函数，结合跟随误差的目标函数和变量范围构造出数学模型，如式(5)。

(5)

经过优化计算，得出x1=1，x2=1，x3=1，跟随误差为822.16。将这组计算结果代入试验平台进行试验，得到跟随误差为820，大于试验数据最跟随误差,误差为2.16，在允许误差范围内，说明应用响应面模型计算跟随误差得到最优值是正确的。同理，建立重复误差的数学模型，见式(6)。

(6)

优化计算得x1=2，x2=1，x3=1，重复误差为1.127。将这组计算结果代入试验平台进行试验，得到跟随误差为1.333，小于试验数据，误差为0.206，在允许误差范围内，说明应用响应面模型计算重复误差所得最优值是正确的。

4多目标遗传算法优化

第3部分对跟随误差和重复误差进行单目标分析计算，并结合试验验证所得计算结果的正确性。这部分将用多目标遗传算法对两个试验指标进行多目标优化，寻找Pareto最优解。根据前面试验数据得到轨迹规划试验指标的跟随误差和重复误差的响应面方程(5)和(6)，建立多目标优化的数学模型。为了确定多目标优化的迭代次数，先找出单目标最优值和迭代次数的关系，见图4。图4中，红线表示跟随误差，绿线表示重复误差。由图4可知，两个指标各自迭代50次就达到最优值。为了保证足够迭代次数来获取最优组合，在采用多目标优化时，将迭代次数设置为60。

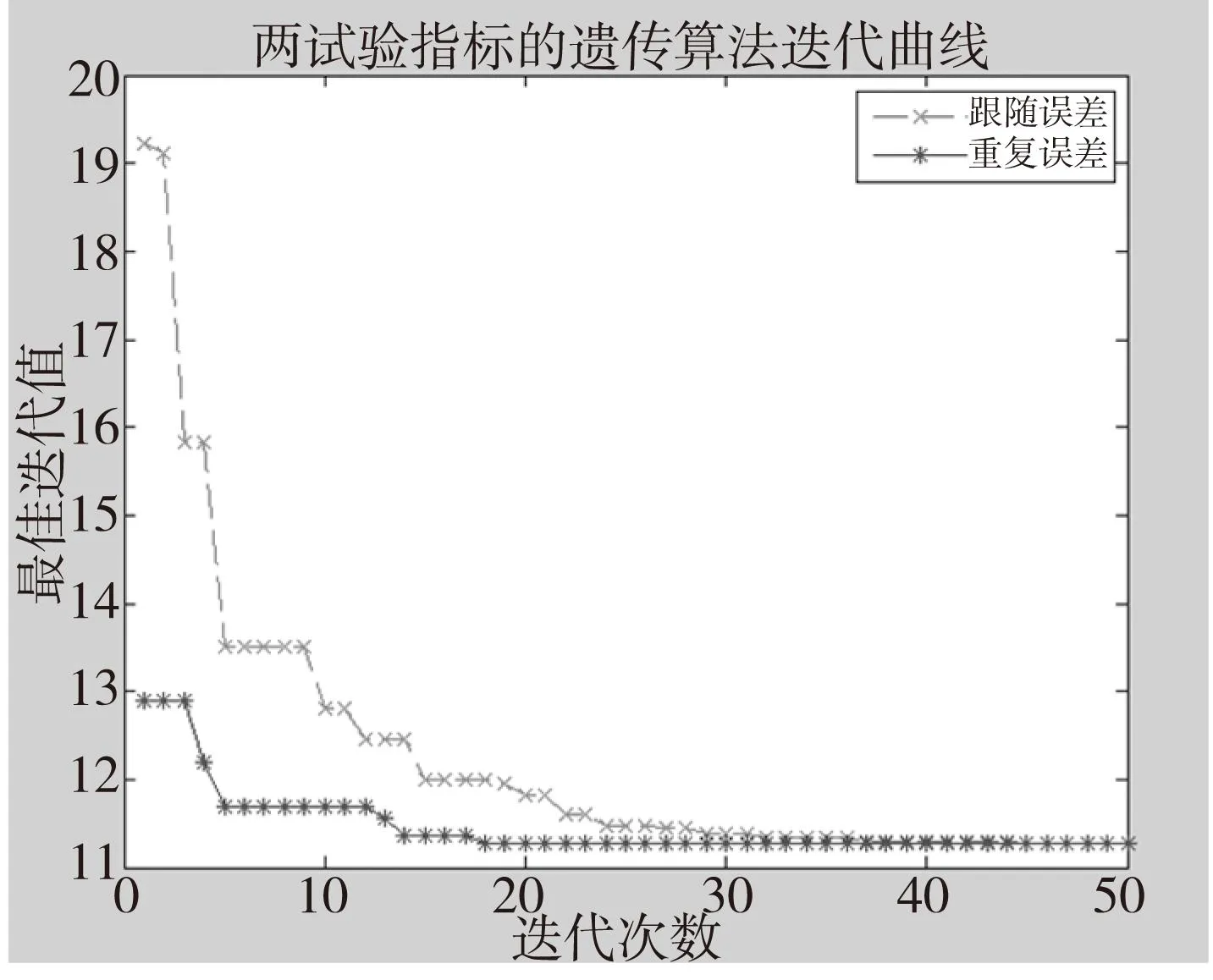
图4　两试验指标的遗传算法迭代曲线

除了确定迭代次数外，应用多目标遗传算法还要设置几个重要参数，参数设置如表4所示。

表4　多目标遗传算法部分参数表

随着每个粒子的不断更新，最终会达到设定的最大迭代次数60，最终绘制出运算得到的所有最优解既Pareto曲线图，如图5。

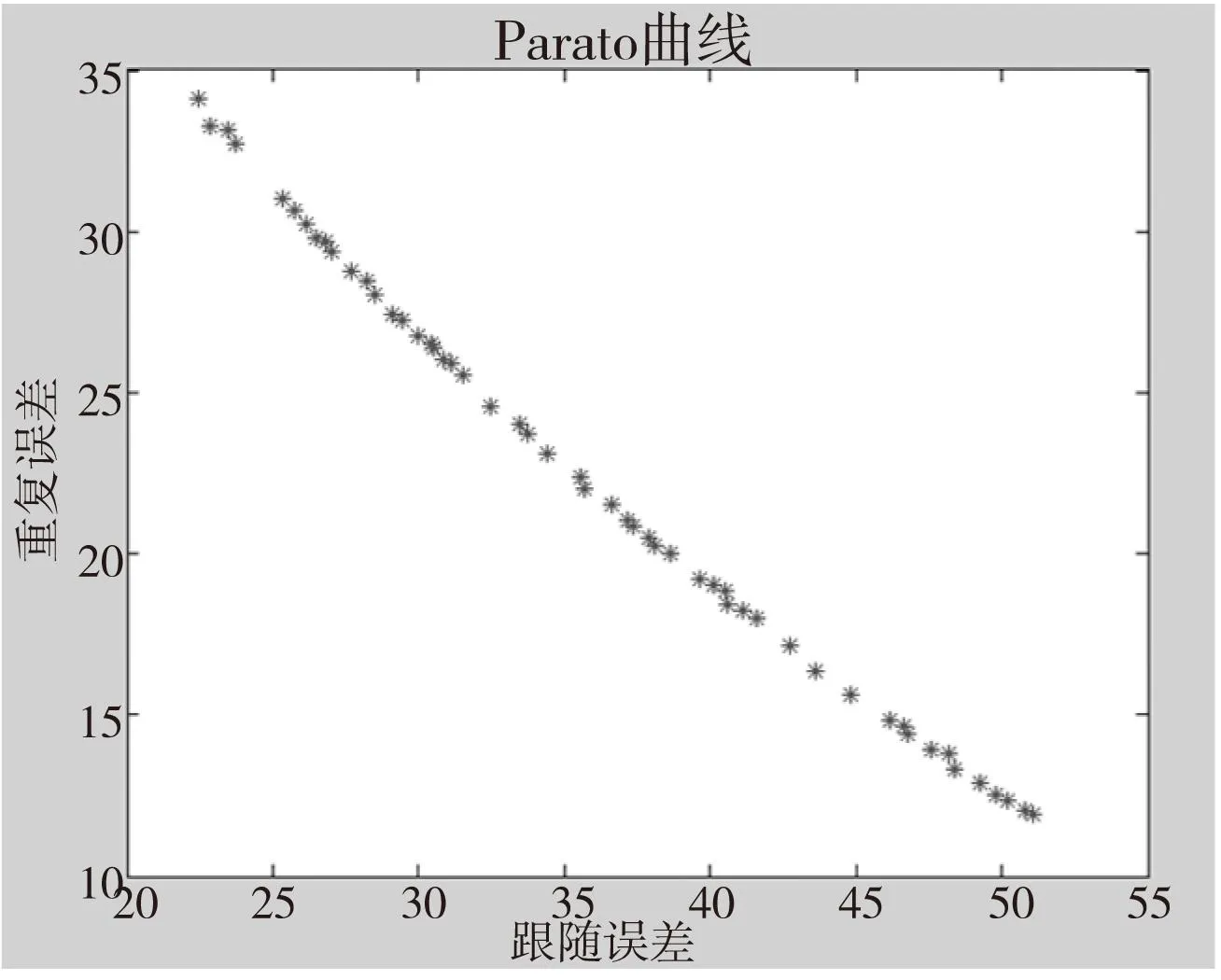
图5　跟随误差-重复误差Pareto曲线图

Pareto曲线图中所有的点都是该优化问题的最优解，从图可知，跟随误差和重复误差这两个试验指标是相互制约的关系，这里我们选取Pareto前沿上的中心点，既点(37.34 ，16.689)作为最优解。该点对应的变量值和最优试验指标以及对于变量值和试验值如表5所示。

表5　优化算法和试验结果对比表

由表5可看出，多目标遗传算法得到跟随误差和重复误差的最优解与试验得到的结果比较接近，证明用响应面模型以及多目标遗传算法优化引线键合混合模式轨迹规划的正确性。

5结束语

本文以PMAC运动控制系统的焊线机为试验平台，利用控制系统中轨迹规划的几种不同控制模式来规划劈刀运动轨迹。结合正交试验设计方法，用正交试验数据建立以不同轨迹规划模式为试验变量与以以劈刀运动轨迹的跟随误差和重复误差为优化目标的响应面模型。先对单目标响应面模型进行可行性分析、计算其最优解并进行试验验证，再用多目标遗传算法对两个试验指标进行多目标优化计算，获得优化目标的Pareto最优解。最后，在焊线机试验平台上验证用响应面模型以及多目标遗传算法优化引线键合混合模式轨迹规划的准确性。试验结果表明，引线键合中采用混合模式轨迹规划相对于单一模式可以提高轨迹运动的精度。

[参考文献]

[1] 徐鹏飞，罗庆生，韩宝玲.新型工业码垛机器人轨迹规划研究[J].组合机床与自动化加工技术,2012(5):70-74.

[2] 李伟光,许阳钊.搬运机器人的轨迹规划[J].组合机床与自动化加工技术,2010(5):83-85.

[3] Wang Yan-jun, Xu Wen-long, Sun Nong-liang. Manipulator trajectory planning based on the cubic triangular Bezier spline[C].Intelligent Control and Automation (WCICA), 2010 8th World Congress on. IEEE, 2010: 6485-6488.

[4] 曹波,曹其新,童上高,等.基于时间最优的搬运机器人运动规划[J].组合机床与自动化加工技术,2012(7): 33-38.

[5] Reynoso-Mora P,Chen Wenjie,Tomizuka M. On the time-optimal trajectory planning and control of robotic manipulators along predefined paths[C].American Control Conference (ACC),IEEE, 2013: 371-377.

[6] 胥晓.引线键合线弧成形规律及其实验平台运动控制研究[D].长沙:中南大学,2013.

[7] 万杰，于海生.改进的双响应曲面法在稳健设计中的应用研究[J].河北工艺大学学报,2011,40(2)：72-75.

[8] 马小姝.多目标优化的遗传算法研究[D].西安:西安电子科技大学，2010.

(编辑赵蓉)本刊欢迎订阅!

欢迎在线投稿!

欢迎刊登广告!

http:∥www.zhjcz.com.cn

The Mixed Mode Trajectory Planning of Wire Bonding Based on Response Surface Model

HUANG Yun-bang,ZHAO Yi-xiang,CHEN Xin

(Guangdong Provincial Key Laboratory of Computer Integrated Manufacturing System, Guangdong University of Technology，Guangzhou 510006,China)

Abstract：The cleaver of welding wire machine are selected as research object,The following error and repetitive error of cleaver trajectory are optimization goals.the variables are different cleaver trajectory planning control modes. Establish the response surface model between test variables and the optimization goals based on orthogonal experiment data,then obtain the Pareto optimal parameters combination by multi-objective genetic algorithm(MOGA) .In the welding wire machine test platform to verify the accuracy of wire bonding mixed mode trajectory planning used the response surface model and MOGA . The results shows that relative to the single mode adopted the mixed mode trajectory planning in wire bonding can improve the accuracy of trajectory.

Key words：response surface model; multi-objective genetic algorithm; trajectory planning; Pareto optimal solutions

中图分类号：TH166;TG506

文献标识码：A

作者简介：黄运榜(1987—)，男，湖北阳新人，广东工业大学硕士研究生，研究方向为机电一体化控制，(E-mail)yun19870908@163.com。

*基金项目：国家973计划项目(2011CB013104)；高等学校博士学科点专项科研基金(20114420110001)；广东省战略性新兴产业专项基金(2011A080303004，2011A081301001)

收稿日期：2015-01-27

文章编号：1001-2265(2015)12-0074-04

DOI:10.13462/j.cnki.mmtamt.2015.12.020