一种基于最小二乘估计的LTEMR电平信号定位方法

一种基于最小二乘估计的LTEMR电平信号定位方法

王卫红1,2,琚波1,杨洁1,程宏兵1

(1.浙江工业大学 计算机科学与技术学院,浙江 杭州 310023；2.软件开发环境国家重点实验室，北京 100191)

摘要：针对现有TD-LTE系统中的定位算法精确度不高的问题，提出一种利用最小二乘估计的LTE-MR定位算法.该算法首先基于电平值，结合自由空间传播模型，测算出手机与临近基站间的距离，采用求质心法抑制误差，利用已知基站坐标和未知定位点坐标表示两点地理坐标的距离，联立方程，最后利用最小二乘法求解特征方程，获得未知定位点的坐标.实验表明：若定位点与服务小区的距离值小于350 m列为精确的点，该算法的定位性能在一天24 h内定位的精确点占比为85.1%，若根据定位点是否落在小区的覆盖范围内来区分，定位点落在小区覆盖范围内的比例是17.4%.

关键词：TD-LTE；基站定位；最小二乘估计；算法精确度

收稿日期：2015-01-26

基金项目：国家自然科学基金资助项目(61340058)；浙江省自然科学基金资助项目(LZ14F020001)

作者简介：王卫红(1969—)，男，浙江临海人，教授，研究方向为图像图形处理、遥感与地理信息系统及信息安全，E-mail：wwh@zjut.edu.cn.

中图分类号：TP391.9

文献标志码：A

文章编号：1006-4303(2015)05-0487-05

Abstract:In view of the problem that accuracy of positioning algorithm is not high for the existing TD-LTE system, a kind of positioning algorithm using the method of least squares estimate and self-designed LTE-MR localization algorithm is put forward in this paper. Firstly, this algorithm uses the level value, combined with free-space propagation model, to calculate the distance between the adjacent base station and mobile phone. This algorithm will suppress errors by using seeking center of mass. It uses the known station location and the unknown anchors coordinates to represent the distance between two geographic coordinates. Then the simultaneous equations can be conducted. Finally, the characteristic equation with Least squares estimation is solved and the coordinates of unknown anchors can be gotten. Experimental results show that if the distance between anchor point and the serving area is less than 350 m, the anchor point can be regarded as a precise point, the positioning performance of the algorithm can reach at 85.1% at precise point positioning ratio in 24 hours. If the distinguishing criteria is based on whether the anchor point will fall within the coverage area in the serving area, the ratio of anchor points that fall within the coverage area of the serving area is 17.4%.

Keywords:TD-LTE; base station positioning; least squares estimation; algorithm precision

A LTEMR level signal localization algorithm based

on ordinary least squares estimation

WANG Hongwei1,2, JU Bo1, YANG Jie1, CHENG Hongbing1

(1.College of Computer Science and Technology, Zhejiang University of Technology, Hangzhou 310023, China;

2.State Key Laboratory of Software Development Environment, Beijing 100191, China)

近年来，随着4G无线通信网络发展，无线蜂窝网的定位功能的应用越来越广泛[1].在军事上，雷达[2]、声呐[3]和传感器网络[4]对于精确定位和传送情报有着重要应用；在生活中，GPS定位、医疗救助定位、求生信号定位和通过移动台破获犯罪等技术也发挥着重要作用.同时，随着时间推移，人们对于定位精度的需求也越来越高[5-7].蜂窝无线定位所采用的方法有很多种，根据特征测量值的不同，基本的定位方法可分为：CELL ID法，信号衰减法，时间测量法，信号到达角度法，GPS定位法[8-10]等.针对精度有限的移动定位算法已有很多学者提出了各方面的改进和优化.其中，Venkatraman S[11]从算法实现角度提出了在Non-line-of-sight (NLOS)环境下高精度的无线定位算法.杨天池等[12]在考虑了基站接收强度的基础上提出了基于TOA/RSS和TDOA/RSS混合的定位算法，提高了传统定位算法的精度.Liu等[13]在静态强度差加入了几何校正算法，进一步优化了定位的精度.

以信号衰减定位技术为基础，提出一种基于信号强度的LTE MR定位方法，结合最小二乘估计OLS法来矫正算法结果.研究目标在于利用基站接收信号强度来实现无线定位技术.对实际服务小区的验证表明，所提出的方法对定位具有较好的效果.

1LTE MR定位算法原理

最小二乘估计OLS法需要构造出相应的特征方程，并使方程的残差无穷小.在该算法中，利用接收基站到手机的距离来构造特征方程.经研究，有两种方式获得该距离，一是利用电平值RSCP求得该距离，二是通过地球两端的地理坐标，求得两点间的距离，当两距离相等时，即可获得特征方程.

利用RSCP获取基站与手机间的距离，首先定义基站的发送功率都为Pt，第i个邻近基站的接收信号功率为RSCPi(单位为dBm).通过测量，获取到RSCP之后，将基站从0开始标序号，接收到信号电平值RSCP最高的邻近基站标为0，其他基站依次标号，同样可得到临近基站的电平值RSCP为

RSCP=Pt-L0

(1)

其中：RSCP为临近基站的电平值；Pt为基站的发送功率；L0为空间损耗.

空间损耗的计算式为

L0=32.45+20lgf+20lgd

(2)

其中f可近似为1 800MHz.

可见当距离d每翻一倍，空间损耗增加约为6.02dBm.将手机与RSCP最高的邻近基站的距离表示为d0，则手机与第i个邻近基站的距离di可得

(3)

其中：RSCP0为临近基站中最高的电平值；RSCPi为临近基站的电平值.

通过转化，即得

(4)

利用两点地理坐标求得距离.接下来，通过地球两端点的地理坐标求出该两点间的距离，地球的模型如图1所示.

图1　地球模型示意图 Fig.1　The model for the earth

地球的半径为R，A和B点可分别视作手机以及接收基站，坐标为A(jA,wB)和B(jB,wB).首先，运用余弦定理，计算A和B点的直线距离,即

AB2=AE2+BE2=CD2+(BD-AC)2=

(OC2+OD2-2OC·OD·cos2∠COD)+

(BD-AC)2=R2(cos2wA+cos2wB-

2coswA·coswB·cos(jB-jA)+sin2wA+

sin2wB-2sinwA·sinwB)=

2R2(1-coswA·coswB·cos(jB-jA)-

sinwA·sinwB)

(5)

继而，求A与B点对应的圆心角，即

(6)

将式(5)结果代入式(6)，得圆心角为

cos∠AOB=1-

coswA·coswB·cos(jB-jA)+sinwA·sinwB

(7)

可通过弧长公式，计算出AB的弧长，即

AB=Rarccos(coswA·coswB·cos(jB-

jA)+sinwA·sinwB)

(8)

得接收基站到手机间的距离，让两距离相等，即是特征方程，通过特征方程即可求出手机的具体位置，特征方程为

cos(jB-jA)+sinwA·sinwB)

(9)

由式(9)可以看出：该特征方程是非线性方程，为了得到手机的所在位置，需要利用非线性最小二乘法进行求解[14-15].常见的方法有牛顿-拉夫逊法、高斯迭代算法、麦夸特算法、变尺度法等，利用牛顿-拉夫森法进行求解.

根据式(9)，共有三个变量，手机经度jB、手机纬度wB以及手机到RSCP最高基站间的距离d0，利用牛顿-拉夫逊法，构造出3维非线性方程，即

(10)

记为F=[f1,f2,L,fn]T,X=[jB,wB,d0]T.

令F(X)=0展开，写成矩阵形式，利用式(12)求得雅可比矩阵，进行k+1次迭代时的关系式

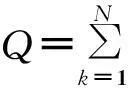
2LTEMR定位算法误差估计

算法实现的是一种理想状况，测算的距离di都无误差，手机的位置刚好在临近基站为圆心，di为半径的圆的交点上，如图2所示，这种情况应该是非常难得的.

图2　无误差距离di的理想情况 Fig.2　The ideal situation without error in di

通常，在无线定位中，由于测量的误差，导致距离di会比真实值偏大或偏小，针对这样的情形，这些以临近基站为圆心，di为半径的圆就会存在不止一个交点，主要的情形如图3～5所示.面对这样的误差，必须制订一定的规则对误差进行估计.

图3　有误差距离di的情况1 Fig.3　The error situation 1 without error in di

图4　有误差距离di的情况2 Fig.4　The error situation 2 without error in di

图5　有误差距离di的情况3 Fig.5　The error situation 3 without error in di

首先求取两圆的交点.已知两圆心坐标P0(x0,y0)，P1(x1,y1)，两圆的半径分别为r0以及r1，模型构建如图6所示.

图6　两圆交点示意图 Fig.6　The schematic diagram of two circular intersection

为了更好地求解两圆的交点，在如上模型中添加了辅助线，根据圆的几何性质可以得

通过转换得

通过以上原理，可得两圆的交点坐标

只使用信号强度最大的3个基站信号.针对现实中测量计算所得的距离存在误差的情况，取出多个(最多6个)正方形标注点中相互离得最近的3个点，求出这3个坐标点的质心作为手机的坐标.

详细的规则步骤如下：

步骤1挑出RSCP最大的3个基站，标记为基站1、基站2和基站3.

步骤2算出各个正方形点的坐标.对于基站i和基站j之间的距离小于di+dj的情况，会得到2个正方形点，如图7所示.

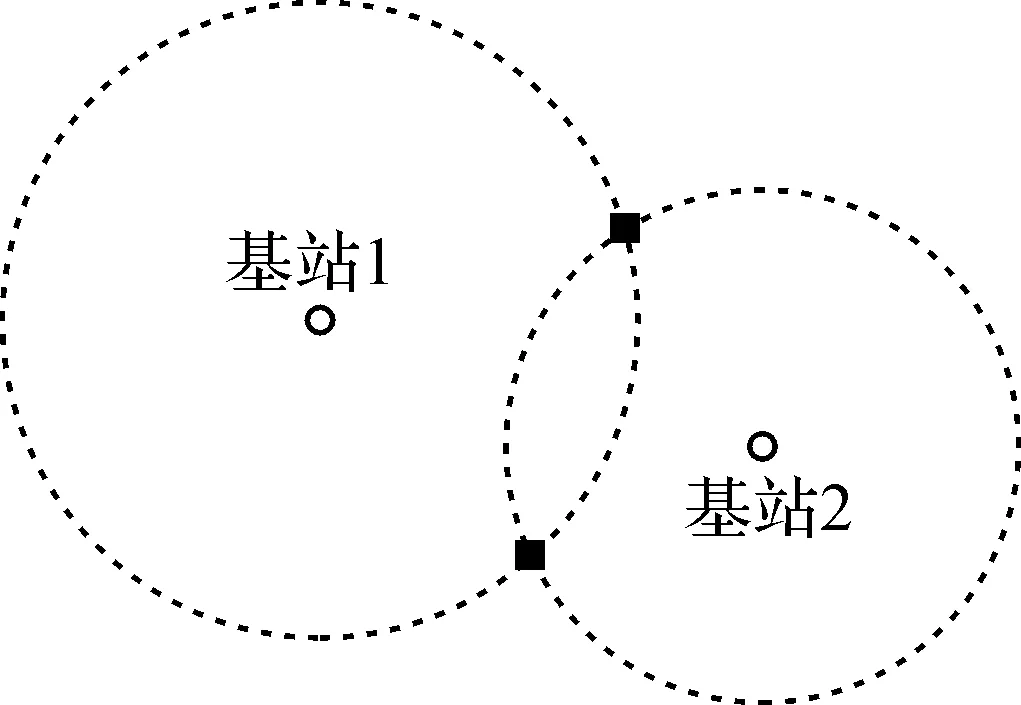
图7　基站间距离小于半径示意图 Fig.7　Schematic diagram of the distance between the base station is shorter than the radius

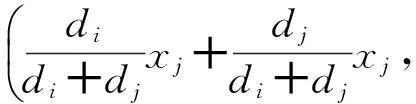
图8　基站间距离大于半径示意图 Fig.8　Schematic diagram of the distance between the base station is longer than the radius

步骤3在所有正方形点中选出3个点.

1)如果有6个正方形点，去掉3个横轴或纵轴是最大或最小的点，剩下的3个就是.

2)如果正方形点少于6个，既两个圆没有交叉点而只得到一个正方形点，这个点必是.挑出离该点最近的一些点，凑到3个.

步骤4求出这三个点的质心.

3LTEMR定位算法的检测与评估

最小二乘估计是计算两种方式获得接收基站到手机间的距离的特征方程，而LTE-ME算法是通过基站接收的电平值，由路径损耗估计出基站到手机间的距离，通过多个基站的测量计算值加权得到手机所在的位置.如表1所示，利用这两种算法分别计算出20组(相同基站不同小区测试两次)测算数据以及手机用户的真实地理位置.

接下来，比较这两种算法的定位精度，此处利用均方误差根来进行比较.平方误差根是利用各测量值误差的平方和的平均值的平方根作为评断结果的优劣指标.均方误差根的求解公式为

(11)

针对上述20组测试数据，根据式(11)求取两算法均方误差根的值，RMSE1=0.028 478，RMSE2=0.339 45.对两算法的均方误差根进行比较，可见RMSE1

为了对笔者算法的效果进行进一步检测，通过对某日在体育场路、保俶路DT测试，得到测试线路图如下.该线路共进行了3轮测试，MRO数据定位结果如图9所示.

图9　体育场路、保俶路、天目山路路线定位点分布图 Fig.9　anchor point distribution of Stadium road, protect Chu road, temmoku mountain road route

序号真实数据手机经度/°E手机纬度/°N最小二乘估计LTE-MR测算手机经度/°E手机纬度/°N经典的LTE-MR测算手机经度/°E手机纬度/°N1120.039930.2321120.044130.2314120.051730.22062120.031330.2303120.030630.2242120.023930.21693120.016430.2097120.028430.2237120.023730.21674120.068030.2417120.036430.2258120.027130.22045120.067630.2461120.028330.2267120.017530.20906120.056230.2711120.036230.2220120.026830.22067120.035530.2316120.037330.2284120.033930.22638120.030530.2186120.040430.2304120.037930.22859120.035230.2314120.038530.2286120.033930.226310120.042730.2213120.026330.2321120.022730.222211120.024430.2248120.033030.2259120.023230.217412120.054430.2665120.033730.2295120.023930.216913120.056430.2533120.034930.2267120.023230.217414120.052830.2571120.039030.2297120.037930.228515120.059930.2567120.038530.2286120.033930.226316120.025330.2214120.039030.2297120.037930.228517120.061130.2480120.032030.2272120.023230.217418120.065030.2498120.039630.2307120.042230.229619120.012930.2192120.037630.2261120.026230.220920120.018630.2089120.037730.2288120.028630.2196

从定位结果来看：天目山路上的MRO定位相对较准确；体育场路上的定位数据整体偏北；保俶路上的MRO定位点相对较为分散.

体育场路上的MRO定位点整体偏北，产生误差的主要原因在于体育场路南面基本没有宏基站，根据定位算法，无法选取南边的基站作为定位的参数，导致定位结果会有偏差，结果如图10所示.

图10　体育场路周边定位点分布图 Fig.10　The anchor point distribution of Stadium road around

相对来讲，保俶北路上的点比较分散，总共有三轮测试，每次测试定位点都在保俶路东面的松木场河西附近，产生偏差的原因可能在于实际环境中河流对算法的影响，后续可引入影响因子改进算法的传播模型.

4结束语

在传统信号衰减定位技术的基础上，提出了一种基于最小二乘法的LTE MR方法.该方法通过把自由空间传播模型计算手机到基站的距离，和地球模型中已知基站坐标和未知定位点坐标求得的距离作差，从而联立方程，引入最小二乘估计法求解方程得到未知定位点的地理坐标.针对真实场景测量计算所得的距离存在误差的情况，引入求质心的方法抑制误差，进而对获取手机到基站的距离进行改进，以获得更精确的定位估计值.实验结果表明：在复杂的城市环境中，该方法具有比传统信号衰减定位方法更好的定位精度，而且基站数目的增加会使得该方法的精度显著上升.

参考文献：

[1]华惊宇,郑志龙,周凯,等.NLOS无线环境中运用最优化原理的定位算法[J].浙江工业大学学报,2014,42(1):93-98.

[2]MIN Jiang, NIU Ruixin, BLUM R S. Bayesian target location and velocity estimation for multiple-input multiple-output radar[J]. IETRadar, Sonar and Navigation,2011,5(6):666-670.

[3]FLUCKIGER M, NEILD A, NELSON B J. Optimization of receiver arrangements for passive emitter localization methods[J]. Ultrasonics,2012,52(3):447-455.

[4]GHOLAMI M, CAI N X, BRENAN R W. Evaluating alternative approaches to mobile object localization in wireless sensor networkswith passive architecture[J]. Computers in Industry,2012,63(9):941-947.

[5]朱国辉,冯大政,周延.一种利用多运动接收站的时差定位算法[J].西安电子科技大学学报,2015,42(2)：38-44.

[6]罗臻,刘宏立,徐琨.基于RSSI的无线传感器网络迭代安全定位算法[J].传感器与微系统,2015,34(1):116-119.

[7]严帅,万新军,杨波,等.无线传感器网络定位算法研究[J].数据通信,2014(2):23-26.

[8]朱江,戚正伟.基于信号衰减和孤立点检测的移动定位算法[J].计算机工程,2010,36(3):280-282.

[9]李红伟,李仕云,纪学军.一种高精度运动多站无源定位算法[J].无线电工程,2014,44(3):24-27.

[10]LIN L X, SO H C, CHAN F K W, et al. A new constrained weighted least squares algorithm for TDOA-based localization[J] Signal Processing,2013,93(11):2872-2878.

[11]VENKATRAMAN S, CAFFERY J, YOU H R. A novel TOA location algorithm using LOS range estimation for NLOS environments[J]. Vehicular Technology, IEEE Transactions on,2004,53(5):1515-1524.

[12]杨天池,金梁,程娟.一种基于TOA定位的CHAN改进算法[J].电子学报,2009,37(4):819-822.

[13]LIU B C, LIN K H. Distance difference error correction by least square for stationary signal-strength-difference-based hyperbolic location in cellular communications[J]. Vehicular Technology, IEEE Transactions on,2008,57(1):227-238.

[14]王理同.带随机线性约束的最小二乘估计的相对效率[J].浙江工业大学学报,2012,40(3):352-354.

[15]许晓辉,王炳忠,刘志.基于最小二乘法的二维条码图像倾斜校正方法[J].浙江工业大学学报,2008,36(3)：250-253.

(责任编辑：刘岩)