温度-离心-振动复合响应分析大规模并行程序设计

牛红攀　肖世富　范宣华

(中国工程物理研究院总体工程研究所　四川绵阳　621999)



温度-离心-振动复合响应分析大规模并行程序设计

牛红攀肖世富范宣华

(中国工程物理研究院总体工程研究所四川绵阳621999)

摘要：再入空间阶段的飞行器受气动加热、过载、流致振动等影响，结构的动力学响应复杂。针对温度、离心载荷对结构振动响应的影响，介绍了温度-离心-振动复合响应分析基本理论，基于PANDA平台设计并实现了大规模并行程序，通过算例验证了程序的正确性。温度-离心-振动复合响应分析技术研究及程序设计工作将为武器系统再入复合环境振动响应分析起到支撑作用，同时为其他领域的多场耦合分析提供借鉴意义。

关键词：PANDA并行分析热力耦合复合响应

战略武器、航天飞机、弹道导弹、返回式卫星等再入空间阶段的飞行器，受气动加热、过载、流致振动的影响，结构的动力学响应复杂。本文将研究结构热应力、离心载荷与振动响应之间的耦合作用，分析温度、离心运动对结构振动响应的影响，研发复合响应分析大规模并行程序，这对于保证飞行器等结构的安全性、可靠性具有重要意义。

温度-离心-振动复合响应分析，本质上是热应力、离心力作用下的刚柔耦合动力学。刚柔耦合系统动力学是多刚体系统动力学的自然延伸，它的各构件之间一般有较大的相对位移运动，而且在运动中要考虑构件的柔性，这使得系统运动的自由度、各构件相互之间的运动学及动力学关系复杂化。在温度场未知的情况下，需要对热传导方程和动力学方程耦合分析。基于线弹性模型，JOHNSTON研究了在温度时变规律已知的情况下太阳能帆板的刚-柔耦合动力学特性[1]。OGUAMANAM研究了中心刚体-薄板的刚-柔耦合特性，基于非线性理论，建立了热流作用下的刚柔耦合系统的动力学模型，并对运动过程中的非线性效应进行研究[2]。李琳等研究了在温度已知的情况下，闭环柔性多体系统的动力学性态，指出热效应会引起各部件加速度和约束力的高频振荡[3]。刘锦阳等基于几何非线性理论，研究了温度场中柔性梁、板系统的动力学问题[4-8]。自2006年起，为提升大规模计算能力，中国工程物理研究院组织研发了PANDA平台。PANDA平台是一个面向实际复杂工程的多物理、大规模并行计算的CAE应用程序基础平台，采用了面向对象的、层次化的、模块化的设计模式[9-17]。为了进一步快速研发大规模结构分析并行程序，从2013年开始，PANDA平台基于JAUMIN框架进行了重构，设计并实现了功能高度可扩充的程序架构，根据模型与算法分离、算法与数据分离的原则，采用算法模块化、模块构件化的开发模式，构建必须的单元库、材料库、载荷库及求解流程库，程序已具有静力、模态、振动响应分析功能，可实现上亿自由度规模的并行计算[18-19]。本文针对飞行器、旋转机构分析需求，将在已有功能基础之上，设计并实现温度-离心-振动复合响应分析功能。

1理论基础

1.1稳态热传导分析

热传导可以定义为完全接触的两个物体之间或一个物体的不同部分之间由于温度梯度而引起的内能的交换。稳态热分析的热传导方程为椭圆型方程，对于三维直角坐标系，稳态热传导微分方程如下：

(1)

式中，T为温度变量，k为温度传导系数，f为源项。

根据有限元理论进一步推导出矩阵形式描述的有限元格式：

[K]{T}={Q}

(2)

其中[K]为热传导矩阵，包含各单元对热传导矩阵的贡献及第三类热交换边界条件对热传导矩阵的修正，即刚度矩阵，具有大型、对称、稀疏、带状分布以及正定、主元占优的特点；{T}为节点温度向量，{Q}为温度载荷向量，包含热流、热交换以及热源引起的温度载荷。

1.2热应力分析

温度改变时，物体由于外在约束以及内部各部分之间的相互约束，使其不能完全自由胀缩而产生的应力，即热应力。求解热应力，既要确定温度场，又要确定位移、应变和应力场，实际上是热和应力两个物理场之间的相互作用，故属于耦合场分析问题。与其他耦合场的分析方法类似，根据耦合方式的不同，存在两种方法：弱耦合和强耦合。弱耦合是先进行热分析，然后将求得的节点温度作为体载荷施加到结构应力分析中；强耦合则是指直接采用具有温度和位移自由度的耦合单元，同时得到热分析和结构应力分析结果。本文采用热力弱耦合分析，求解步骤为：首先由热传导方程和边界条件求出温度分布，再由热弹性力学方程求出位移和应力。

线性热弹性问题的有限元格式为：

[K]{u}={Pf}+{Pth}

(3)

式中，[K]为整体刚度矩阵，{u}节点位移向量；{Pf}为结构载荷引起的节点载荷向量；{Pth}为温度应变引起的节点载荷向量。其中

(4)

(5)

{εth}=α(T-T0)[1 1 1 0 0 0]T

(6)

其中[B]为几何矩阵，[D]为弹性矩阵，{εth}为节点温度应变向量，α为热膨胀系数，T0为节点参考温度，T为节点温度。

热应力可由如下公式计算得到：

[σ]=[D]([B]{u}-{εth})

(7)

从上述线性热弹性问题的有限元计算公式中可以看出与线弹性问题有限元求解方程的区别是载荷向量中包括由温度应变引起的温度载荷{Pth}以及在计算应力时包含温度应变引起的初应变项{εth}。当结构的温度场已经求得时，带入上述表达式即可进一步求出结构的位移、应变及应力。

1.3结构动力学特性分析

考虑热应力、旋转软化效应和动力刚化效应，结构的动力学控制方程为

[Kc]+[Ks]){u}={F}

(8)

式中[M]为质量矩阵，[C]为阻尼矩阵，[K]为传统刚度矩阵，[Kc]为旋转软化效应矩阵，[Ks]为应力刚化矩阵，包括热应力和载荷的影响，{F}为外力向量，{u}为位移向量。

1.3.1旋转软化效应

在动力学分析时，旋转结构与其他结构相比有一个很大不同：旋转软化效应。对于每个节点均有3个自由度的空间结构，在节点上旋转软化效应矩阵可表示为

(9)

式中：[M]为3×3的质量矩阵，ωx为绕X轴的角速度，ωy为绕Y轴的角速度，ωz为绕Z轴的角速度。

1.3.2应力刚化效应

当弹性体受到较大的外力将引起较大的变形时，采用线性化的应变与位移关系不能真实的反应弹性体的应变和应力状态，忽略这种几何非线性的影响直接导致了对弹性体的刚度估计偏低。考虑几何非线性的影响可得出单元刚度矩阵为：

=[K0]e+[S]e

(10)

公式(10)中第一项即传统的刚度矩阵，第二项为应力刚化矩阵。应力刚化矩阵[S]e可表示为：

(11)

式中[S0]为应力刚化子矩阵，表达式为

(12)

其中[Sm]为柯西应力，[G]为形函数的梯度。

2程序设计

2.1软件总体架构

采用“基于框架开发应用软件”的现代软件开发理念，基于JAUMIN框架，在程序设计时首先考虑并行，根据模型与算法分离、算法与数据分离的原则，从偏微分方程弱形式出发，构建必须的单元库、材料库、载荷库、计算流程库。软件的整体层次结构如图 1所示，包括应用支撑层、有限元共性层、有限元个性层与应用服务平台。其中应用支撑层主要为软件提供数据支撑服务，包括JAUMIN变量的注册、管理与使用、模型节点与模型单元数据管理、自由度映射表建立与管理、数值输出以及对称矩阵等常见工具箱；有限元共性层提炼了静力与振动响应分析软件的有限元计算共性部分，包括单元、材料、场数据、约束、载荷、求解流程等；有限元个性层针对不同的结构分析建立个性分析模块，如针对结构应力分析，需要建立结构应力单元、结构材料、结构应力场、节点位移约束、节点力、压力、重力、静力求解流程、模态求解流程等；应用服务平台即在此基础之上建立专业领域的数值仿真平台，同时具有二次开发功能等。

PANDA静力与振动分析软件的主要模块如图2所示，包括单元模块、材料模块、场模块、约束模块、载荷模块、求解流程模块等，其中FEManager为有限元方法接口，管理各个模块，通过对各模块的管理实现有限元方法的计算。

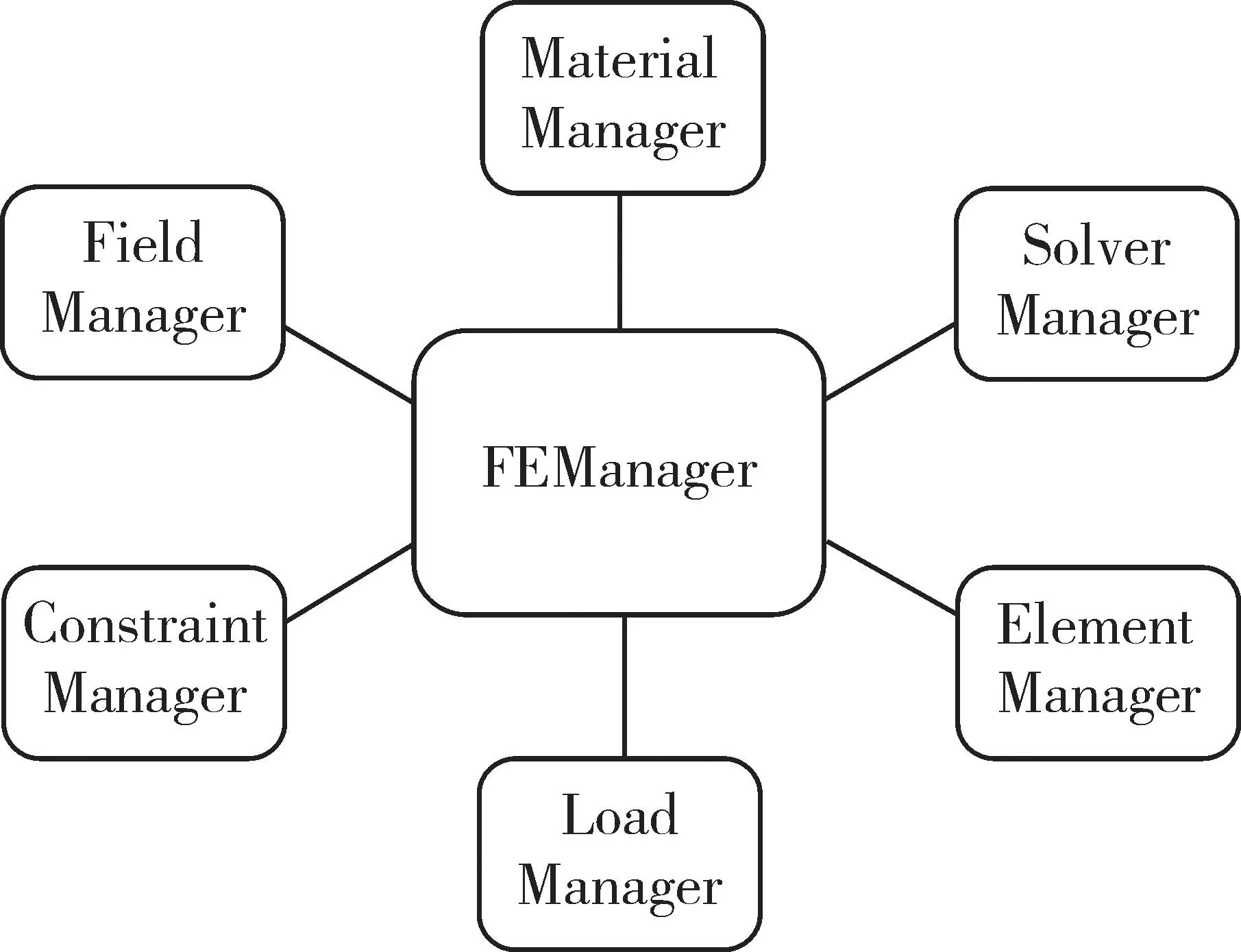
图2　PANDA-STAVIB软件主要模块及模块关系

2.2热力弱耦合设计

弱耦合分析，即各物理场单独分析，通过数据交互实现耦合。软件初步实现了相同Patch下的弱耦合分析，即各物理场采用同样的网格拓扑。各物理场单独进行求解，通过场进行数据交互，多步迭代之后，可得到各物理场的解，如图 3所示。对于热力弱耦合分析，首先求解热扩散方程得到温度场的分析，之后根据热弹性方程计算得到结构的热应力和变形。

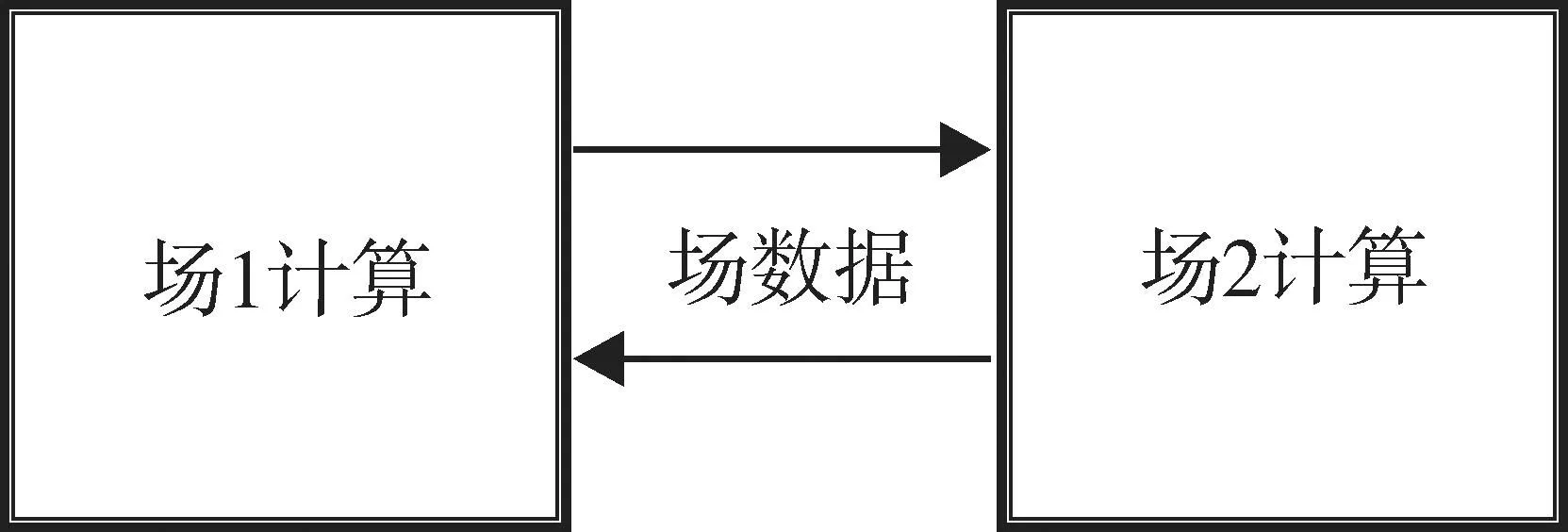
图3　弱耦合分析示意图

2.3序贯分析设计

软件采用了多求解步设计实现序贯分析，每个求解步即单独的一个分析类型，可执行一个完整的求解流程，数据均保存在场中，各求解步均可存取场中的数据。如图 4所示，温度-离心复合振动响应分析时，结构应力、温度等数据均保存在场中，首先热力分析计算得到热应力分布，在模态分析时考虑热应力带来的预应力影响，之后根据模态分析的结果采用模态叠加法进行振动响应分析。

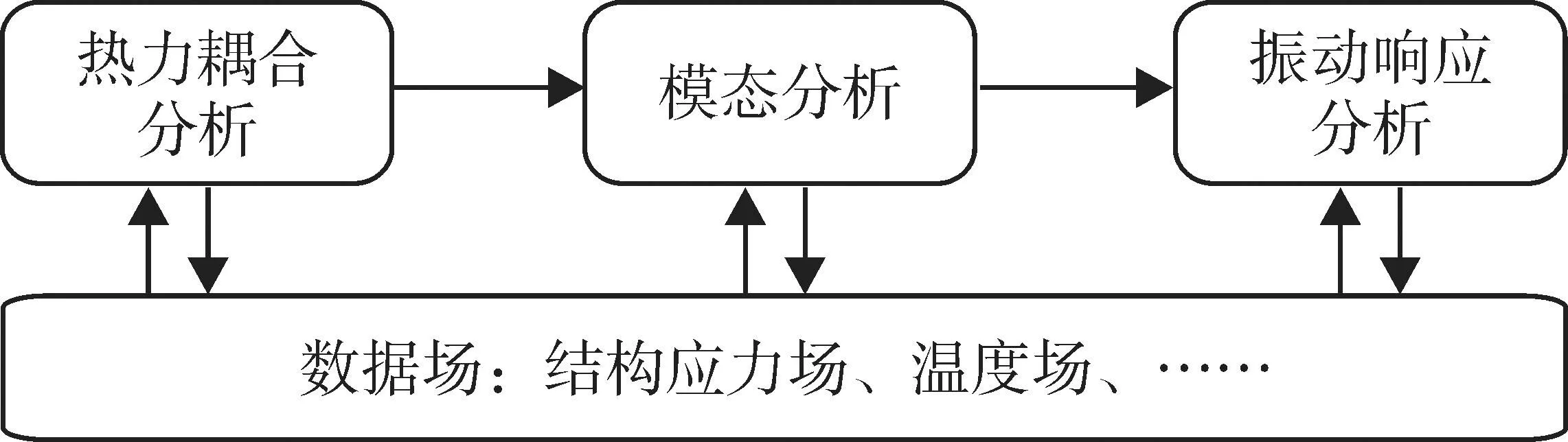
图4　温度-离心复合振动响应分析示意图

3算例测试

算例所采用的模型为梁结构，材料参数如表 1所示。梁结构的尺寸为1 m×1 m×10 m。采用六面体单元进行网格划分，六面体单元的边长为1，整个模型节点数为44，单元数为10，如图5所示。施加边界条件为绕端部进行旋转，旋转角速度为100 rad/s，绕轴旋转端的温度为100 ℃，自由端温度为20 ℃。

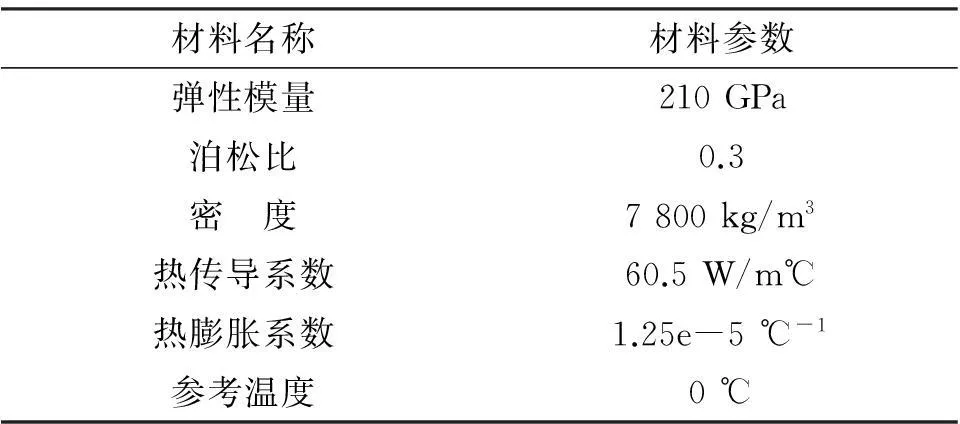
表1　算例采用材料的材料参数

图5　算例模型网格示意图

采用线性分析，模态计算结果如表 2所示，从表中数据对比可以看到PANDA的计算结果与ANSYS基本一致，验证了包含动力刚化效应模态算法的正确性。

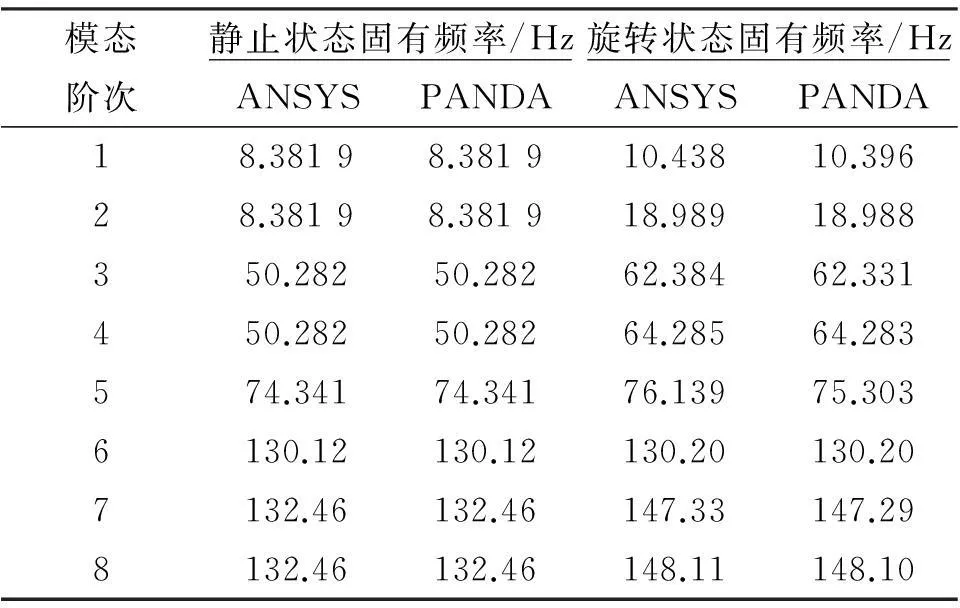
表2　算例模态分析结果

在坐标(0，0，10)处施加Y方向振幅为1e6 N的简谐力，响应点坐标为(0，1，10)，阻尼比取0.01，利用PANDA程序计算的静止状态下的谐响应曲线与温度-旋转状态相比如图 6所示，可看到温度-离心-振动耦合无论在固有频率上，还是在振幅上均有不同，说明了热应力、离心力对振动响应的影响。

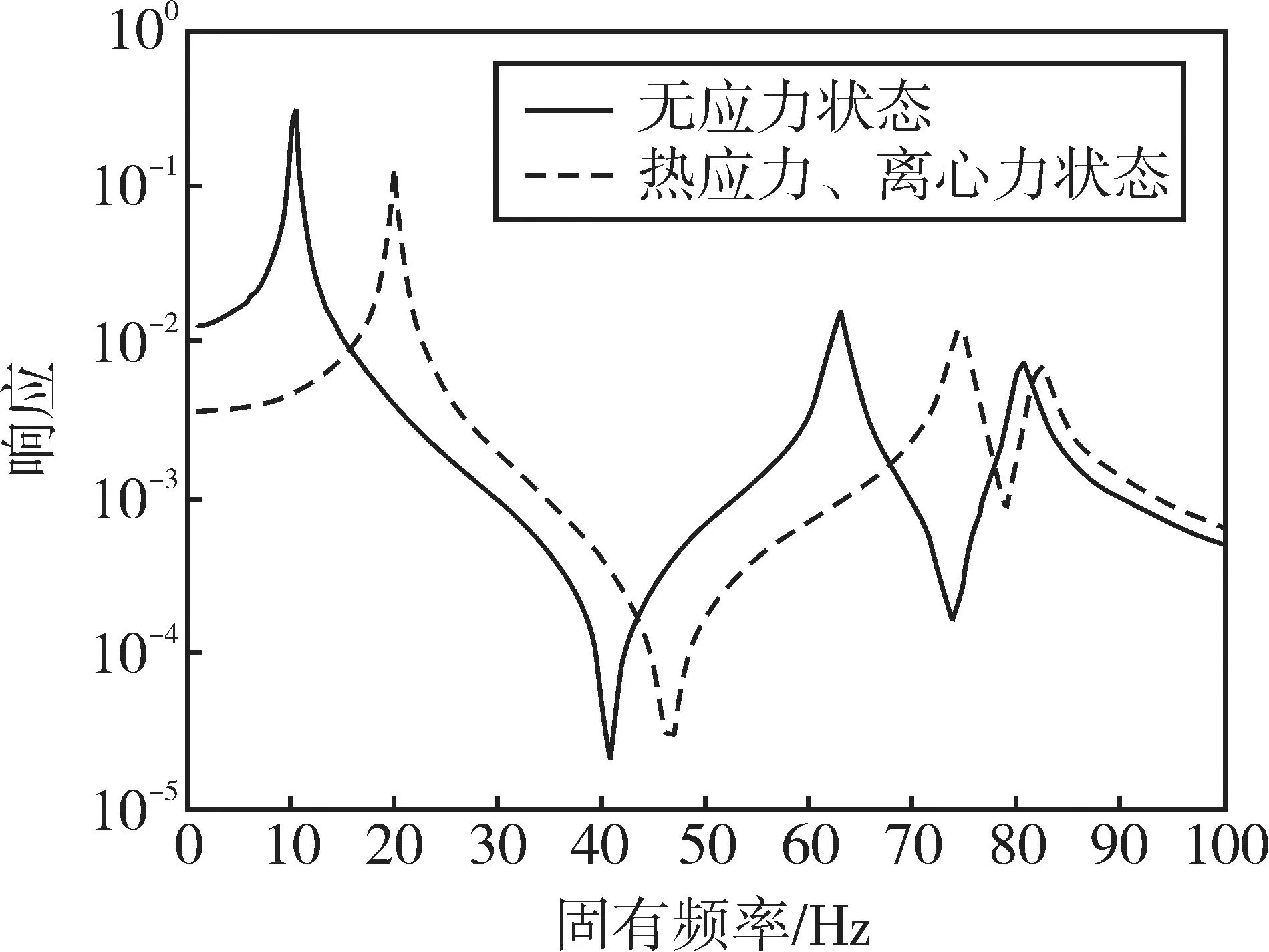
图6　不同状态下的谐响应曲线对比

采用同样的计算参数，分别利用PANDA和ANSYS计算了响应点处的谐响应，计算结果如图7所示，从图7可看到热应力、离心力下的PANDA计算的谐响应曲线与ANSYS一致，验证了PANDA温度-离心-振动复合响应分析的正确性。

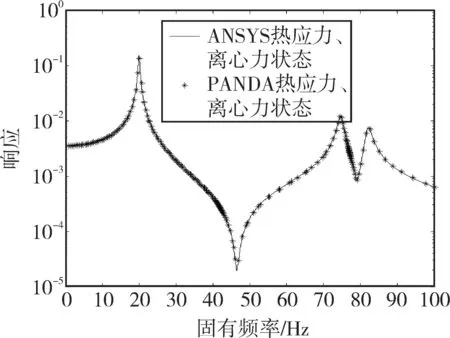
图7　PANDA与ANSYS计算结果对比

4结论

本文研究了温度-离心-振动复合响应分析算法，分析了热应力、旋转软化效应和动力刚化效应，建立了考虑热应力的旋转结构控制微分方程，基于PANDA平台进行了程序设计和代码实现，最后设计了温度-离心-振动复合响应分析算例验证了程序的正确性。本工作将为武器系统再入复合环境振动响应分析起到支撑作用，同时为其他领域的多场耦合分析提供借鉴意义。

参考文献

[1]JOHNSTON J D, THORNTON E A. Thermally induced attitude dynamics of a spacecraft with a flexible appendage [J]. Journal of Guidance, Control, and Dynamics, 1998, 21(4): 581-587.

[2]OGUAMANAM D, HANSEN J, HEPPLER G. Nonlinear transient response of thermally loaded laminated panels[J]. Journal of Applied Mechanics, 2004, 71(1): 49-56.

[3]李琳, 刘锦阳. 计及热效应的闭环柔性机械系统的动力学分析 [J]. 机械科学与技术, 2006, 24(12): 1491-1494.

[4]刘锦阳, 崔麟. 热载荷作用下大变形柔性梁刚柔耦合动力学分析 [J]. 振动工程学报, 2009, 22(1): 48-53.

[5]刘锦阳, 洪嘉振. 温度场中的柔性梁系统动力学建模[J]. 振动工程学报, 2007, 19(4): 469-474.

[6]刘锦阳, 李彬, 陆皓. 计及热应变的空间曲梁的刚-柔耦合动力学 [J]. 固体力学学报, 2007, 28(1): 30-36.

[7]刘锦阳, 袁瑞, 洪嘉振. 考虑几何非线性和热效应的刚-柔耦合动力学 [J]. 固体力学学报, 2008, 29(1): 73-77.

[8]刘锦阳, 袁瑞, 洪嘉振. 考虑热效应的柔性板的刚-柔耦合动力学特性 [J]. 上海交通大学学报, 2008, 42(8): 1226-1232.

[9]FAN X H, WU R A, CHEN P. Scalability study on large-scale parallel finite element computing in Panda frame[J]. Applied Mechanics and Materials, 2012, 117:489-492.

[10] 陈成军, 柳阳, 张元章, 等. 基于 PANDA 的并行显式有限元程序开发 [J]. 计算力学学报, 2011, 28(B04): 204-207.

[11] 嵇晓宇, 郝志明, 莫军, 等. 面向对象有限元并行计算框架 PANDA 求解器的服务构件化设计与集成 [J]. 计算机辅助工程, 2011, 20(1): 9-14.

[12] 李健, 郝志明, 宁佐贵. 基于 PANDA 框架的并行有限元模态分析程序开发和应用 [J]. 计算机辅助工程, 2011, 20(1): 29-32.

[13] 史光梅, 何颖波, 吴瑞安, 等. 面向对象有限元并行计算框架 PANDA 研究进展[A].见：proceedings of the 中国计算力学大会’2010 (CCCM2010) 暨第八届南方计算力学学术会议 (SCCM8) 论文集[C]. 2010.

[14] 史光梅, 何颖波, 吴瑞安,等. 面向对象有限元并行计算框架 PANDA [J]. 计算机辅助工程, 2010, 19(4): 8-14.

[15] 孙乐, 何颖波, 吴瑞安,等. 面向对象有限元并行计算框架 PANDA 的多物理场耦合服务 [J]. 计算机辅助工程, 2011, 20(1): 19-23.

[16] 孙乐, 莫军, 肖世富, 等. 复杂结构黏弹性问题的大规模并行计算研究 [J]. 应用数学和力学, 2014, (S1): 226-231.

[17] 徐建国, 石正军, 郝志明,等. 基于 PANDA 框架的非线性静力学有限元并行计算程序设计和初步验证[J]. 固体力学学报, 2010, (S1): 294-298.

[18] FAN X, WANG K, XIAO S, et al. Some Progress on Parallel Modal and Vibration Analysis Using the JAUMIN Framework [J]. Mathematical Problems in Engineering, 2014.

[19] 孙运见, 孙乐. 基于 Jaumin 的等参单元算法框架设计[J]. 计算机辅助工程, 2015,(1):63-67.

E-mail:402niuhp@caep.cn

Massively Paralleled Program Design of Thermal-Centrifugal-Vibration

Composite Response Analysis

NIU Hong-pan, XIAO Shi-fu, FAN Xuan-hua

(InstituteofSystemsEngineering,CAEP,Mianyang621999,Sichuan,China)

Abstract:The dynamic response of the space vehicles, which in reentry space phase, is complicated with the effects of aerodynamic heating, overload, flow induced vibration, and so on. This paper focuses on the vibration response with thermal and centrifugal loads effects. Firstly, the basic theory of Thermal-Centrifugal-Vibration response is introduced. Massive paralleled program based on PANDA platform is designed and implementation. Finally a test is designed to verify the program correctness. Thermal-Centrifugal-Vibration composite response analysis paralleled program plays a support role in space vehicles in reentry space phase, as well provides reference for other multi-field coupling analysis.

Key words:PANDA; Paralleled simulation; Program design; Thermal-solid coupling

中图分类号：O313.7；TP391

文献标志码：A

文章编号：1671-8755(2015)04-0042-05

作者简介:牛红攀(1981—)，男，博士，高级工程师，研究方向为复杂系统结构力学大规模并行计算、柔性多体动力学。

基金项目:国家自然科学基金青年基金(11402244)。