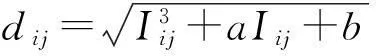云端核心医学信息秘密动态分享方案

孙天凯，鲍　蓉，张仁伟

(1.大连理工大学 电信学部，辽宁 大连　116024；2.徐州工程学院，江苏 徐州　221018)



云端核心医学信息秘密动态分享方案

孙天凯1,2，鲍蓉2，张仁伟2

(1.大连理工大学 电信学部，辽宁 大连116024；2.徐州工程学院，江苏 徐州221018)

摘要：针对可视密码中的欺骗、不诚实等问题，以核心医学信息为载体，利用素数域上的椭圆曲线，研究并实现了一种适用于云端核心医学信息的秘密动态分享方案.通过选取合适的椭圆曲线参数值，对原始信息进行一次加密，在椭圆曲线加密体制下，对分享的子信息，使用私钥进行再次加密认证.通过加密、动态分享以及Lagrange 插值多项式方案的融合，提高了现存方案的安全性、隐蔽性，达到了秘密信息分享的高效性、实用性.实验结果表明，本方案也具有较高的计算效率以及信息恢复效率.

关键词：椭圆曲线；可视密码；动态分享；身份认证

云计算技术的迅猛发展，为数据的共享提供了强有力的技术支撑.然而，云平台在提供信息共享的同时，也面临着数据被泄露、篡改以及假冒等一系列问题[1-3].云端核心信息的秘密共享问题成为了当前研究的热点问题.Shamir和Blakely于1979年分别提出了秘密共享的概念.近年来，私密共享技术被予以重视并得到快速发展，但目前该技术还有很多缺陷和不足[4-6].本文利用椭圆曲线密码，给出了一种多密钥，可防欺诈的动态分享方案.

1关键技术介绍

1.1可视密码

可视密码是一种秘密共享方案(n,k).该方案提供了一种将一个秘密的图像分割成多个(n)子图像的方案，它不需要任何密码学的计算，就可以通过k个子图像获得原来的秘密图像.即使是一个具有无穷计算能力的攻击者，也不能在拥有的子秘密数量少于一个给定值(k)时获得关于秘密图像的任何信息[7].

1.2椭圆曲线密码算法

作为数论、代数几何等多个数学分支交叉点的椭圆曲线，起初被认为是一个纯理论学科，1985年Victor Miller和Neal Koblitz分别提出了将椭圆曲线理论应用到密码学的构想.从此，椭圆曲线密码体制(elliptic calve cipher system，ECC)相关问题的研究成为了一个十分活跃的密码学研究方向.ECC体制的一大重要特性在于，可以使用更短的密钥，达到同样的安全级别，密钥短意味着，安全防护过程中，只需要更小的带宽和存储要求[8].

2方案的总体设计

2.1设计目标与原则

设计一个基于椭圆曲线与可视密码的多用户秘密动态分享认证方案.基于动态秘密分享方案的特点，方案的设计考虑如下原则：

1)信息分享的动态多选择性.

2)信息质量的可控性，在对私密信息进行加密、恢复以及认证的过程中，保证信息在对比度、大小比例等方面不受影响.

3)结果的可验证性，针对参与者欺骗、信息篡改，参与者个数不足等问题具有强鲁棒性.

2.2认证方案的实现流程

本方案融合可视密码以及椭圆曲线，实现对私密信息的多重高效防护.该方案分为私密信息加密与私密信息验证两大模块.系统的具体实现流程如图1所示.

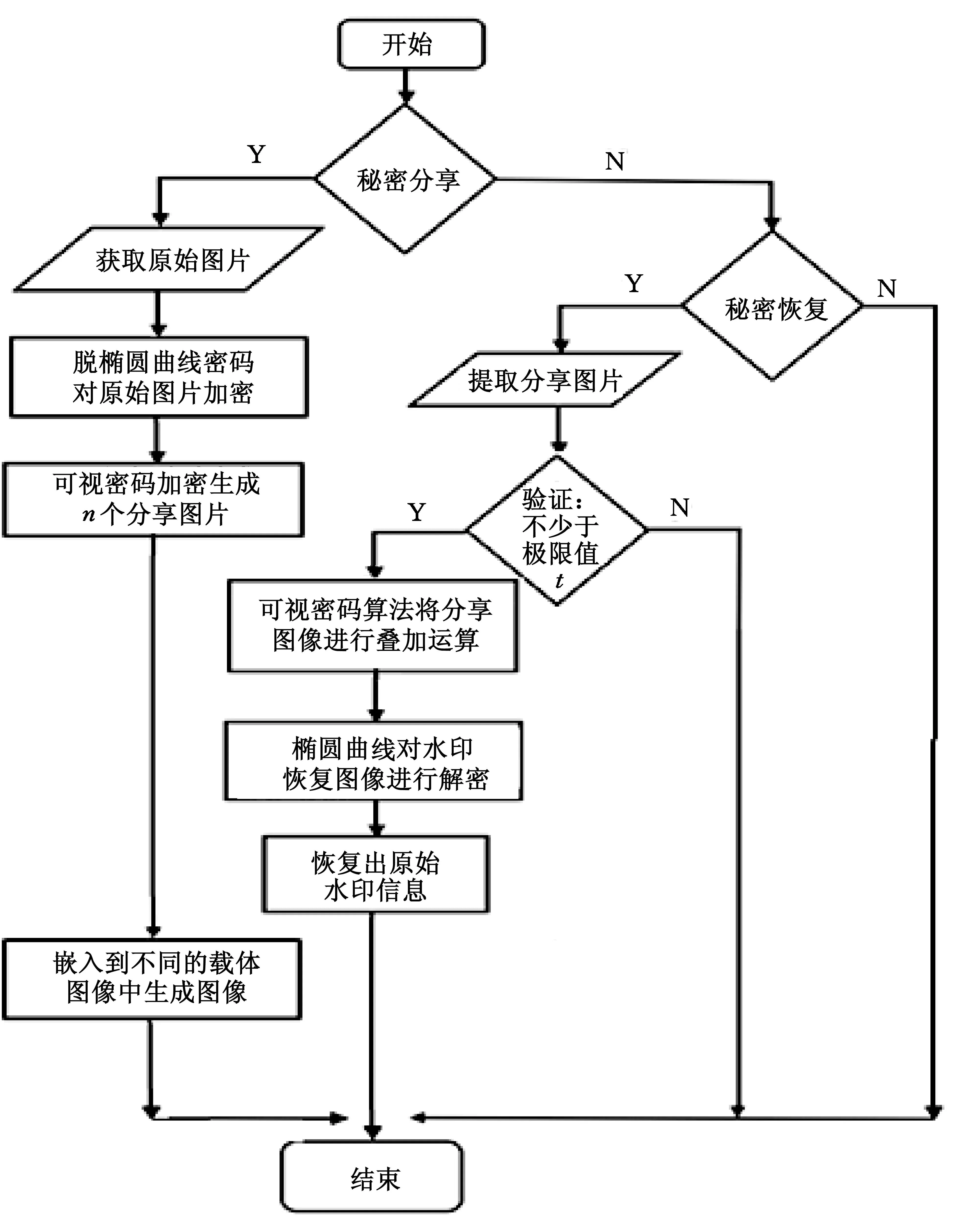
图1　认证方案的实现流程图

3系统实现

图2、图3给出了秘密信息分享及恢复过程示意图，其详细实现过程如下所示.

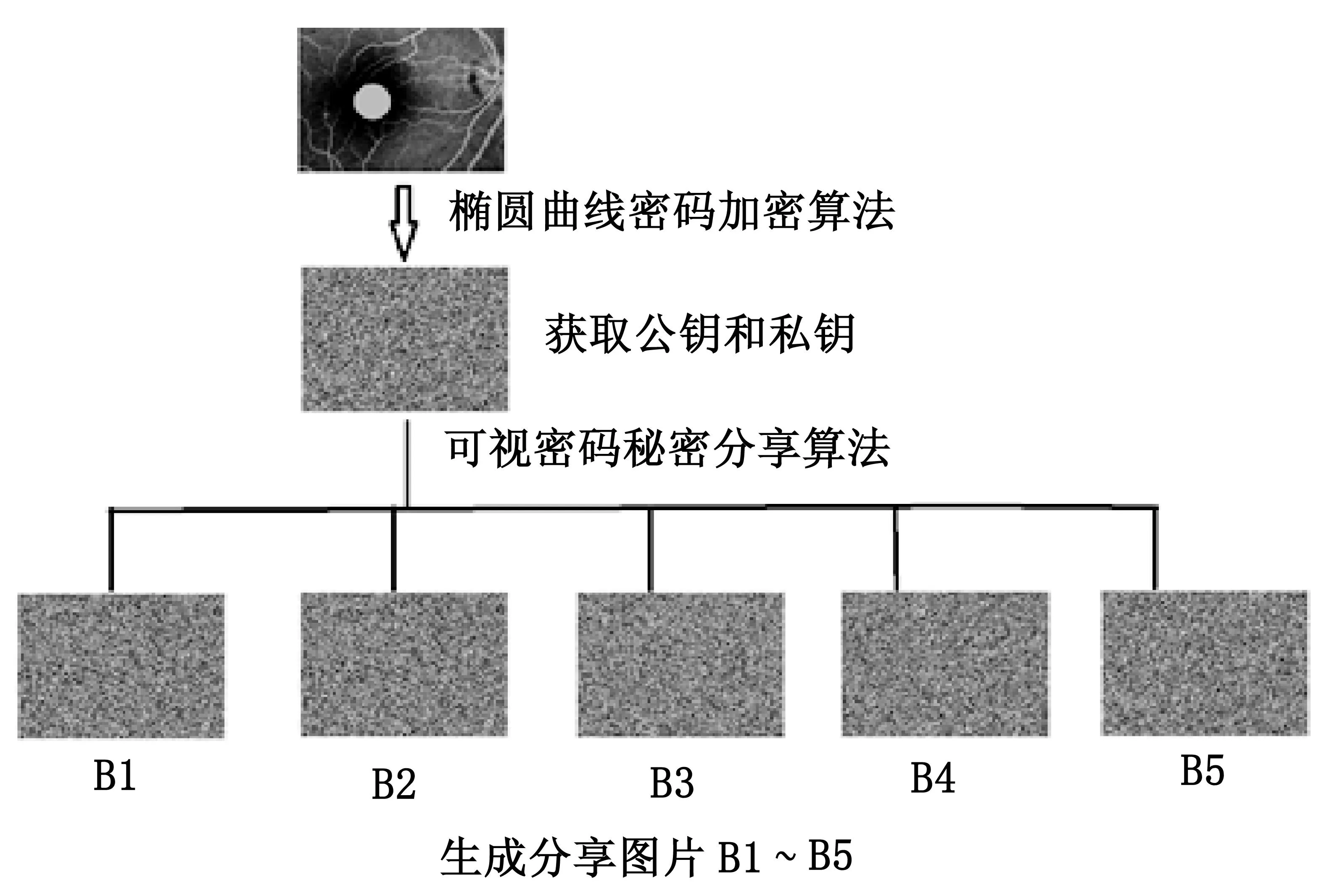
图2　私密信息分享块实现流程

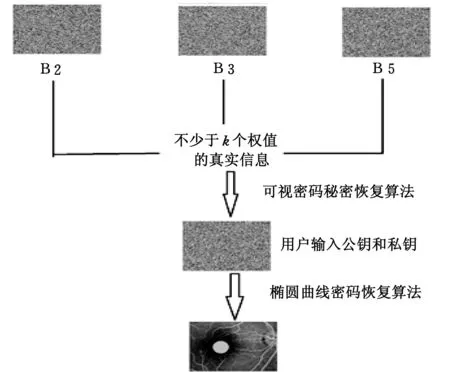
图3　私密信息恢复模块实现流程

假定可信中心CA，其主密钥k0，共有m个参与者Pi(i= 1,2,…,m)，其身份标识ID为(i= 1,2,…,m).在有限域GF(q)(其中q为素数)上选取一条安全的椭圆曲线 ，其方程式如下所示：

E(Fq):y2=x3+ax+b,(q>3),

其中a，b∈GF(q)，且4a3-27b2≠0;G为E(Fq)上选定的一个基点，G点的阶为大素数n(n至少是160 bit的素数).CA公开参数(a,n,k0,G).

3.1加密过程

用户A首先生成一条椭圆曲线，其方程为

y2=x3+ax+b,(其中x≥0).

用户B将Im通过公共网络发送给用户A，并进行如下操作：

1)B首先将认证信息数字化，得到Im的图像矩阵(Iij)m×n，其中(Iij)m×n的元素为Iij,则有

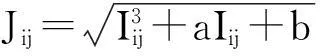
由此，求出点P(Iij，Jij)，其中1≤i≤m,1≤j≤n;

2)利用A的公钥Q，任取一个整数k，其中k∈[1,n-1],计算P=kG=(x1,y1)；

3)计算：kQ=(x2,y2);

for(i=1;i

for(j=1;j

If(P!=Q)

λ[i][j]=y2+J[i][j]/x2+I[i][j];

c[i][j]=(λ[i][j])2+a/2y2;

}

}

输出c[i][j],得出加密后的信息矩阵(cij)m×n；

4)以信息矩阵(cij)m×n的元素作为像素点的灰度值，作出另一幅图像以Ic表示.则信息Ic就是信息Im的秘文.用户B将(P，Ic)发送给用户A.

3.2解密过程

当用户A收到从B发来的(P，Ic)后，用自己的私钥d进行解密，具体如下：

2)A计算：dP=(x2,y2).

因为dP=d(kG)=dkG=k(dG)=kQ=(x2,y2);

3)A通过循环计算

for(i=1;i

for(j=1;j

if(P!=Q)

λ[i][j]=y2+(-d[i][j])/x2+c[i][j];

//其中λ[i][j]是点-R’和点kP确定直线的斜率

c[i][j]=(λ[i][j])2+λ[i][j]+x2-c[i][j];

}

}

输出I[i][j],得出信息矩阵(cij)m×n；

4)将信息矩阵(Iij)m×n的元素作为像素点的值恢复出信息Im.

秘密图像分享Lagrange 插值多项式，采用Shamir提出的实数域的Lagrange插值算法方案[1].

4实验结果分析

为了验证算法的有效性及相关性能，在Myeclipse10.0、JDK1.6的平台上对该方案进行了一系列的验证测试.

假定5人拥有核心私密共享权，在验证时需要至少3人，提供各自持有的私密信息.待保护的核心医学信息如图4所示，秘密分享结果如图5所示.

图4　待保护的核心医学信息

图5　秘密分享结果

可视密码图片由版权所有者持有.版权信息认证过程如下所示.

进入还原信息过程，选择待还原信息(个数大于权限值)，图6给出了正确还原出的秘密信息.还原信息个数小于权限值(图7给出了测试结果，左一为原始版权私密信息，左二为还原后的错误私密信息).还原信息中存在虚假信息，无法恢复出源信息(图8给出了测试结果).

图6　正确还原出的私密信息

图7　还原图片个数小于权限值

图8　存在虚假信息的测试结果

5结语

针对云端核心医学信息私密分享的问题，本文融合可视密码、椭圆曲线以及Lagrange 插值多项式等技术，设计并实现了一种动态秘密分享方案.从大量的测试结果可知，本方案在功能上具有较好的安全性，在时间和空间上均具有较高的效率，同时大大增加了算法被破解的难度.

参考文献：

[1] 韩妍妍.可视密码技术的研究[D].西安：西安电子科技大学，2009.

[2] 郭帅,谢淑翠.椭圆曲线上一个动态秘密共享方案[J].计算机工程与应用,2013,49(6):97-99.

[3] 肖立国,钟诚,陈国良.基于椭圆曲线密码体制的动态秘密共享方案[J].微电子学与计算机,2002(1):30-31.

[4] Wang M S,Chen W C.A hybrid DWT-SVD copyright protection scheme based on k-means clustering and visual cryptography[J].Computer Standards & Interfaces,2009,31(4):757-762.

[5] Lei B Y,Soon Y,Li Z.Blind and robust audio watermarking scheme based on SVD-DCT[J].Signal Processing,2011,91(8):1973-1984.

[6] Song W,Hou J J,Li Z H,A novel zero-bit watermarking algorithm based on logistic chaotic system and singular value decomposition[J].Acta Physica Sinica,2009(7):4449-4456.

[7] Wu X T,Sun W.Robust copyright protection scheme for digital images using overlapping DCT and SVD[J].Applied Soft Computing,2013,13(2):1170-1182.

[8] 范畅,茹鹏.一种基于ECC的动态秘密共享方案[J].计算机仿真.2012,29(12):131-134.

[9] Rawat S,Raman B.A blind watermarking algorithm based on fractional Fourier transform and visual cryptography[J].Signal Processing,2012,92(6):1480-1491.

[10] 王小云,王明强.公钥密码学的数学基础[M].北京：科学出版社,2014.

(编辑武峰)

Research on the Dynamic Sharing Scheme of Core Medical

Information in the Cloud

SUN Tiankai1,2,BAO Rong2,ZHANG Renwei2

(1.Faculty of Electronic Information and Electrical Engineering, Dalian University of Technology, Dalian 116024, China;

2.School of Information and Electrical Engineering, Xuzhou Institute of Technology, Xuzhou 221008, China)

Abstract:In view of the problems of deception and dishonesty in visual cryptography,the dynamic sharing scheme of core medical information in the cloud is studied and realized in this paper by taking the core medical information as the carrier and using the elliptic curve of prime number field.By selecting the appropriate parameters of elliptic curve,the original information is encrypted once,and the shared sub information is encrypted and identified again with the private key in the elliptic curve encryption system.Through encryption,dynamic sharing and Lagrange interpolation polynomial scheme,the security and concealment of the existing scheme is improved to achieve the high efficiency and practicality of the secret information sharing.The experimental results show that this scheme is also efficient in computation and information retrieval.

Key words:elliptic curve; visual cryptography; dynamic secret sharing; identity authentication

中图分类号：TP3

文献标志码：A

文章编号：1674-358X(2015)04-0079-06

作者简介：孙天凯(1982-), 男,山东聊城人，讲师,博士研究生，主要从事信息隐藏，数据认证等研究.

基金项目：国家自然科学 (61370145,61173183);江苏省产学研联合创新项目(BY2013020)；徐州市科技计划项目(XM13B126)；徐州工程学院青年基金(XKY2015312)

收稿日期：2015-06-07