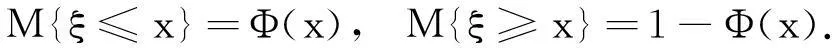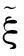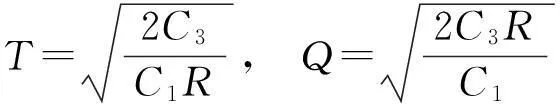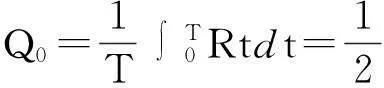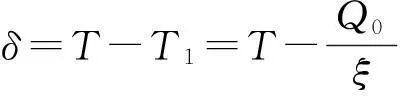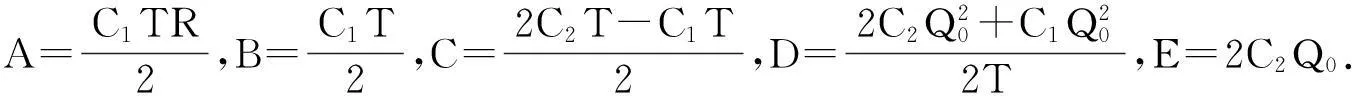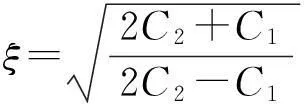基于不确定理论的EOQ模型及库存风险分析

黄世华1，杨兆兰1，曹建军2，秦燕燕3

(1.兰州文理学院师范学院, 甘肃兰州　730030；

2.西北师范大学地理与环境科学学院,甘肃兰州　730070；

3.甘肃省白龙江林业管理局林业科学研究所,甘肃兰州　730070)

基于不确定理论的EOQ模型及库存风险分析

黄世华1，杨兆兰1，曹建军2，秦燕燕3

(1.兰州文理学院师范学院, 甘肃兰州730030；

2.西北师范大学地理与环境科学学院,甘肃兰州730070；

3.甘肃省白龙江林业管理局林业科学研究所,甘肃兰州730070)

摘要：基于不确定理论，研究了需求为不确定变量(不是随机变量和模糊变量)的库存风险控制最优策略，以风险最小化为目标建立了库存风险模型.确定了“之字形分布”下的最佳需求估计值，得出了需求为不确定变量时的经济订货批量和订货周期的修正公式.应用数学软件Matlab，对该模型进行仿真计算，结合灵敏度分析方法，分析了模型参数变化对库存风险控制的影响.

关键词：不确定变量；之字形分布；经济订货批量；库存风险模型

收稿日期：2015-03-27;修改稿收到日期:2015-08-26

E-mail:shihuah@sina.com

基金项目:国家自然科学基金资助项目(41461109)

作者简介：黄世华(1969—)，女，甘肃永靖人，教授.主要研究方向为数理应用及模型.

中图分类号：O 227

文献标志码：标志码：A

文章编号：章编号：1001-988Ⅹ(2015)06-0028-07

Abstract:In order to achieve the goal of minimizing risk on inventory,based on the uncertainty theory,the optimal strategy of inventory control under uncertain demand is explored,and the risk model of inventory is established.Furthermore,the best demand estimated value is confirmed under the“zigzag distribution”,and the formulae of economic order quantity and the ordering cycle with uncertain variables are further corrected.Following this,using the mathematical software Matlab,the model’s simulation values are calculated,and the effect of parameter variation on inventory risk control is analysed by combining with sensitivity analysis method.

EOQmodelbasedonuncertaintytheoryand

inventoryriskanalysis

HUANGShi-hua1，YANG Zhao-lan1，CAO Jian-jun2，QIN Yan-yan3

(1.NormalCollege,LanzhouUniversityofArtsandSciences,Lanzhou730030,Gansu,China；

2.CollegeofGeographyandEnvironmentSciences,NorthwestNormalUniversity,Lanzhou730070,Gansu,China；

3.ResearchInstituteofForestryScience,BailongjiangForestryManagementBureau,Lanzhou730070,Gansu,China)

Keywords:uncertainvariables；zigzagdistribution；economicorderquantity；inventoryriskmodel

0引言

不确定理论由Liu[1]于2007年建立，并于2010年得到了进一步完善[2]．该理论是具有规范性、对偶性、次可列可加性和乘积测度的数学系统，是公理化数学的一个分支，是用于研究主观不确定现象的数学工具．不确定集是不确定理论的主要内容之一，2010年Liu[3]首次提出不确定集，并于2012年给出了不确定集的新定义[4].不确定集是定义在不确定空间上的极值函数，不同于Zadeh[5]定义的模糊集和Matheron[6]定义的随机集．不确定集、模糊集和随机集虽都是极值函数，但它们之间存在本质的不同.主要区别在于依据的测度不同，即不确定集依据的是Liu[1]定义的不确定测度，模糊集依据的是Zadeh[5]提出的可能测度，随机集依据的是Kolmogorov[7]定义的概率测度．目前，不确定理论已成功应用于信息科学、自动化、经济学、工业工程和管理科学等领域中．

库存问题一直是生产管理领域的探索前沿，许多新概念都是在对其进行系统研究和深刻反思的基础之上提出的．自Wilson于1905年首次提出经济批量公式(EOQ)以后,存贮理论发展异常迅猛，许多学者对库存模型中经济批量研究做了很多工作．李温红[8]提出仓库容量有限条件下订货销售存贮的EOQ模型；宋国芳等[9]对有批量折扣不允许缺货的EOQ问题进行了研究；杨益民等[10]讨论了关于生产销售存贮的EOQ问题；罗兵[11]等探讨了存货影响销售和顾客等待的特价商品EOQ模型；万延花等[12]以利润最大化为目标，利用利润的两阶段函数给出了再制造零部件和再装配产品的最优批量．Ilkyeong等[13]研究了产品寿命周期在随机变量条件下，资金的时间价值和通货膨胀因素对EOQ模型的影响；Gupta-Vrat[14]在假定存货影响销售率是初始库存水平的函数的情况下，研究了成本最小的库存模型；Padmanabhan-Vrat[15]在假定存货影响销售率是任意时刻库存水平函数和变质率是常数的情况下，提出了变质物品存货影响销售率的库存模型；王道平等[16]探讨了需求和采购价格均为时变的易变质物品EOQ模型；冯颖等[17]研究了在给定时间范围内多种易变质产品的一次性联合订购决策，使库存系统总成本最小问题；李明芳等[18]研究了延期支付期限与订货量相关情形下的EOQ模型．Kacpp-Staniewski[19]和Park[20]最先将模糊分析方法引入库存管理,之后许多学者利用模糊分析方法研究了库存问题，如Li等[21]提出了两种模型：一种是关于需求随机和成本模糊的，另一种是关于成本确定和需求模糊的，通过模糊数的模糊排序，他们提出了获得最佳订购量的途径；Chang等[22]和Wu[23]分别研究了订购量是三角形和梯形模糊数的EOQ模型;Eynan等[24]提出了在库存费用可变、需求随机的等周期库存系统下的最优订货周期和安全库存；Geunes等[25]分析了参数可变、需求随机的库存系统中再订货点和订货量决策问题；Shao等[26]建立随机需求下多产品的报童模型;张福利等[27]从零售商的需求将会受到库存约束的角度探讨了不确定需求条件下制造商的退货政策;邱若臻等[28]在需求分布不确定条件下，建立基于最大最小方法的多周期库存鲁棒优化模型；程硕等[29]对市场需求不确定情况下的多周期生产批量决策优化问题进行了研究；赵明等[30]将经典报童问题扩展为基于随机模糊需求的自由分布报童模型；赵建华等[31]基于不确定理论的运算法则，在不确定环境下对投资收益与风险问题的模型进行了研究.

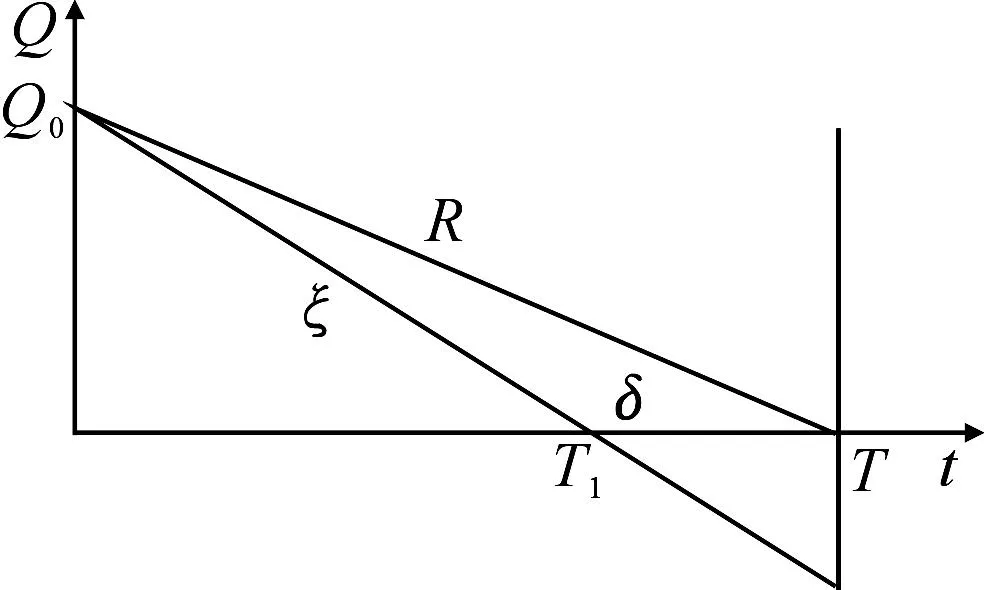
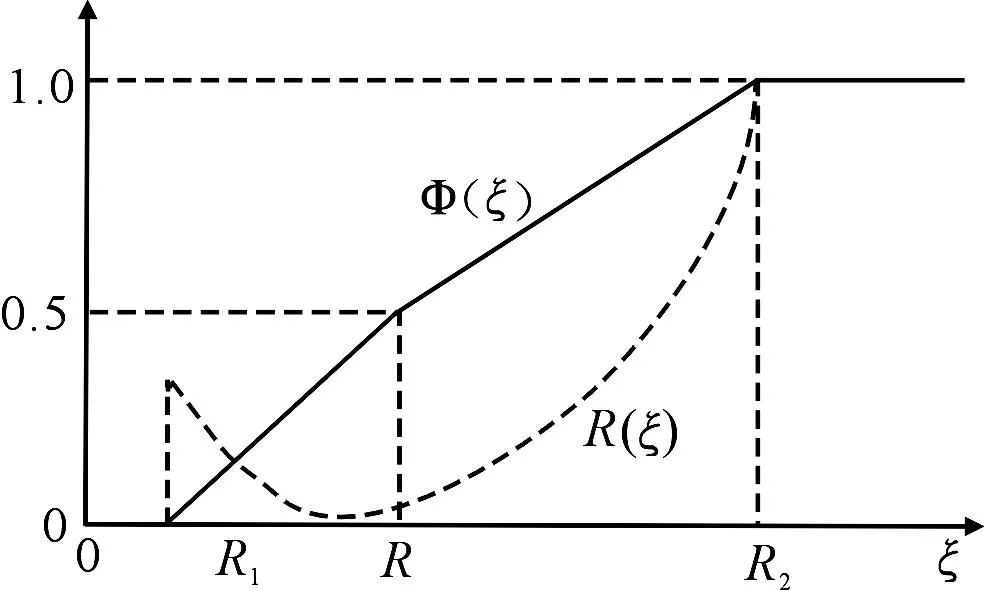
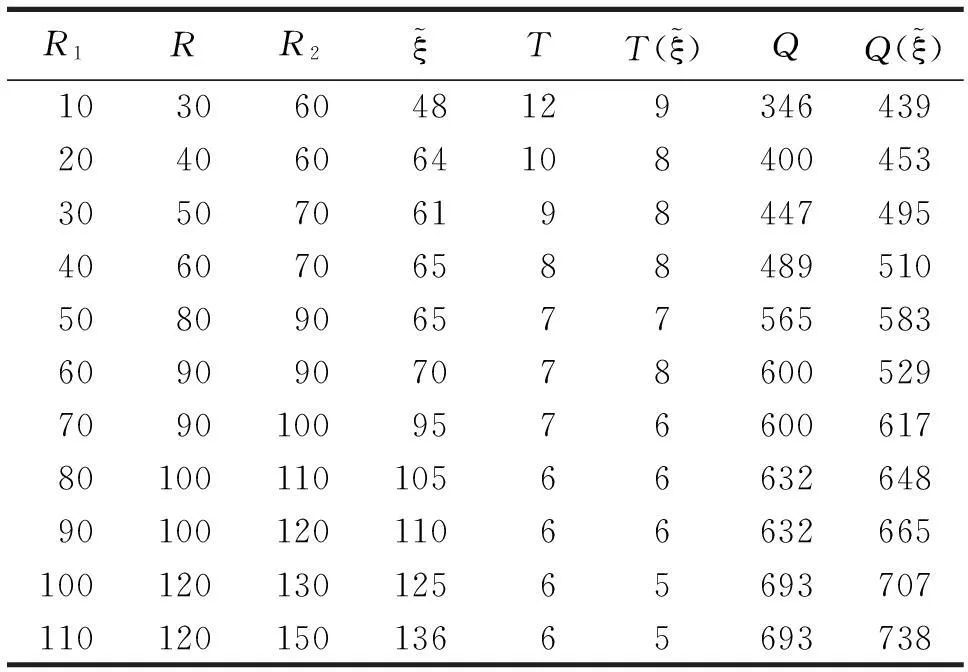
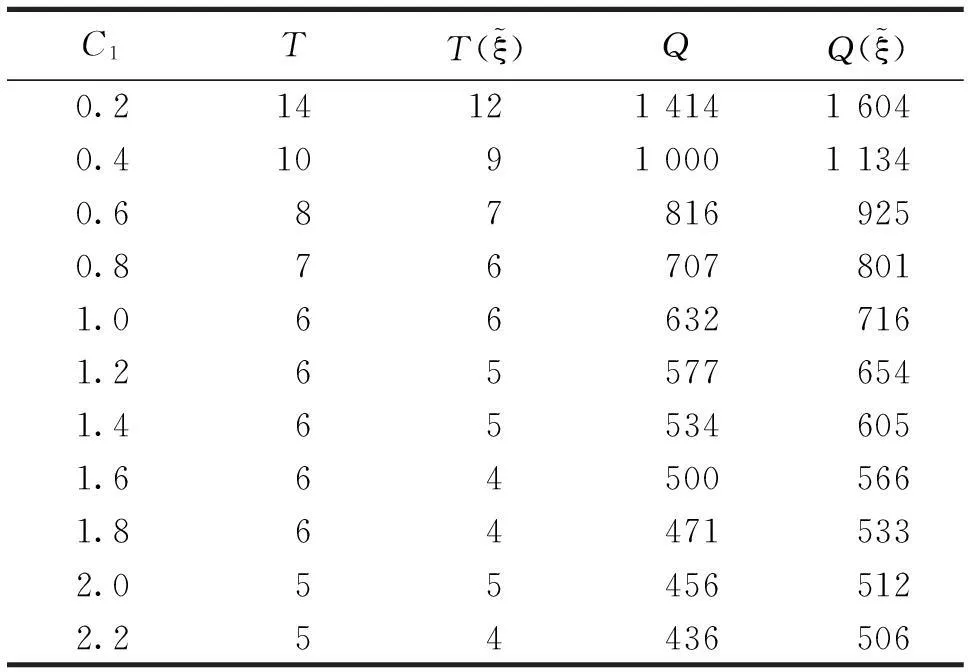
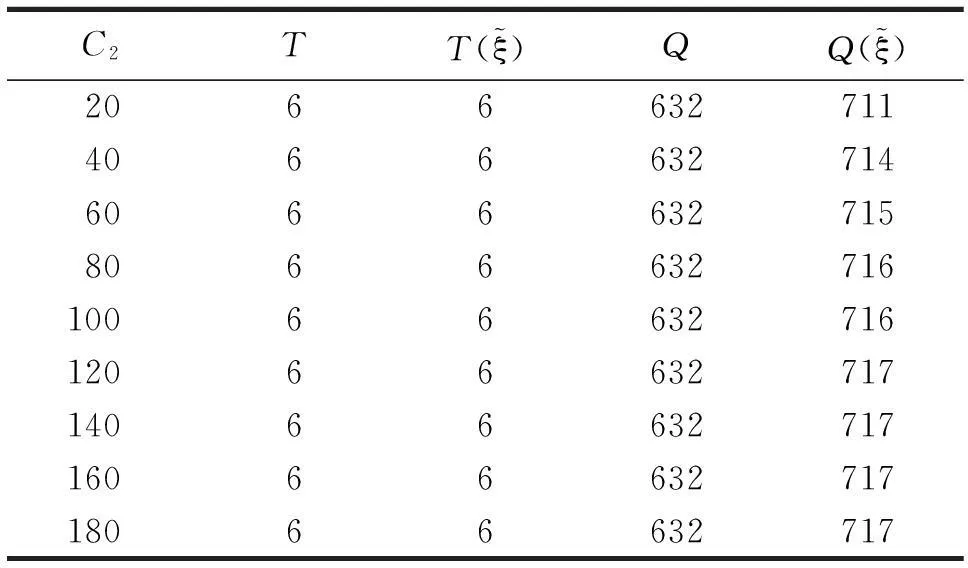
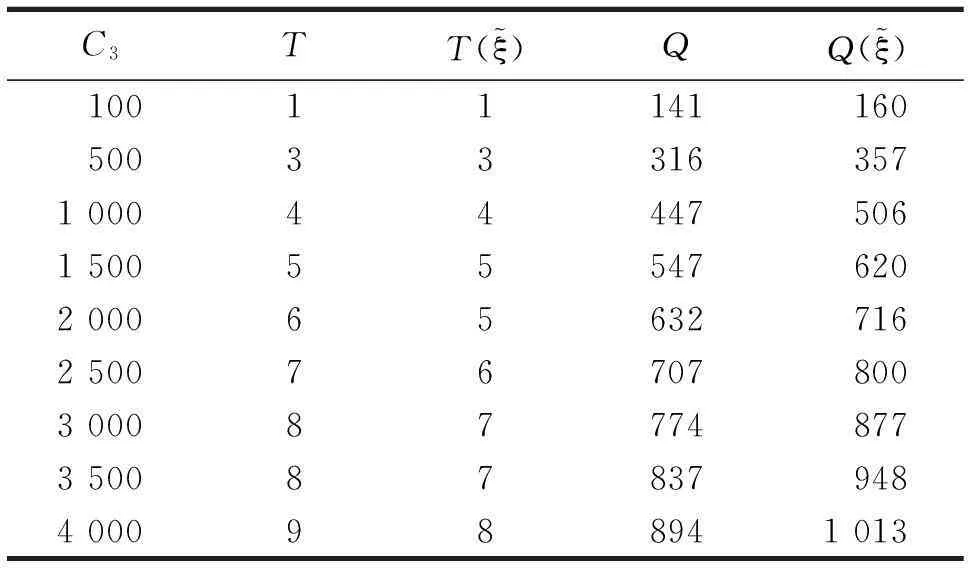
通过对以往文献的分析发现，大多数库存研究的重点都集中在关于定常需求的库存控制问题研究、关于时变需求的库存控制问题研究、关于依赖于库存水平需求的库存控制问题研究、关于随机需求的库存控制问题研究、关于随机模糊需求和模糊随机需求的库存控制问题研究、多种物品的库存控制问题研究上．目前,研究需求为不确定变量(不是随机变量和模糊变量，也不是随机模糊变量和模糊随机变量)的库存控制问题较少,故本文在不确定理论基础上,研究需求为不确定变量的库存风险控制最优策略，以风险最小化为目标建立库存风险模型，并确定“之字形分布”下的最佳需求估计值，得出了需求为不确定变量时的经济订货批量和订货周期的修正公式．最后，应用数学软件Matlab，对该模型进行仿真计算，并对各个参数进行灵敏度分析，说明修正后的经济订货批量和订货周期优于经典经济订货批量和订货周期，是经典库存问题的一种推广．

1预备知识(不确定性理论)

设Γ是一个非空集合，L是Γ上的一个σ-代数，在σ-代数L中的每一个元素Λ叫做一个事件；M是一个集函数，如果L满足规范性、自对偶性、可列次可加性，那么称M为一个不确定测度.不确定测度是一个从L映射到[0，1]的函数，三元组(Γ，L，M)被称为是一个不确定空间.

随机变量可以用它的密度函数来刻画，模糊变量可以用它的隶属函数来刻画，而对一个不确定变量，最简单有效的方式是用它的分布函数来刻画.

定义2[3]一个不确定变量ξ的不确定分布Φ定义为:对∀x∈R,Φ(x)=M{ξ≤x}.

定义3[2]一个不确定变量ξ称为之字形的，如果它具有之字形不确定分布，记为

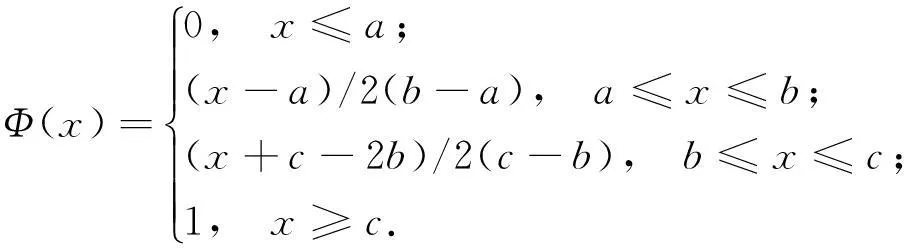
其中a,b,c是实数且a

定理1[3]假设一个不确定变量ξ具有连续的不确定分布Φ(x)，那么对于任意的实数x,有

2模型假设与符号说明

参照EOQ模型的基本假设，本文做如下假设，其中(v)，(vi)是对经典假设的推广.

(i)允许缺货，当库存量下降到某定值时提前订货.

(ii)不考虑通货膨胀或者通货紧缩.

(iii)只考虑单个产品订购.

(iv)不存在数量折扣，不存在物品变质，不存在存货影响销售率等情况.

(v)每次订货量可以不同，但必须是整数.

(vi)单位时间的需求量为不确定变量ξ，ξ服从Z(R1,R,R2)的之字形分布.

符号说明：

3建模与求解

众所周知，在经典的库存模型中进货周期T和经济订货批量Q分别为：

通常在短时期内，单位存贮费C1和订货费C3都不变，但由于市场、生产或自然环境的变化都有可能引起对库存物资需求的变化，需求速度很难保证是一个不变的常数.利用经典库存公式确定的库存量很可能未来面临两种风险：一是需求突然下降，周期内库存物资积压而带来的相关损失，二是需求突然增加，周期内库存物资缺货而造成的损失，我们将这两种损失统称为库存风险.引起库存风险的因素有很多，假定库存风险仅由需求量的变化而引起，那么库存风险将围绕需求速度而变动.假定我们没有关于需求速度不确定变化的统计资料，只有对需求速度变化范围以及在该范围内出现的可能性进行估计，即单位时间的需求量为一个不确定变量ξ，其不确定分布为：

R是最有可能的需求速度(即客观环境不发生意外变化条件下的正常需求速度)，R1和R2分别是一旦发生变化后的最小可能需求速度和最大可能需求速度，Φ(ξ)是需求速度在变化范围[R1，R2]内的可能性主观估计(图1).当实际需求速度ξ大于正常需求速度R时将会造成缺货，这时应当在正常需求速度R的预计库存为零之前再次订货;当实际需求速度ξ小于正常需求速度R时将会造成积压，这时应当在正常需求速度R的预计库存为零之后再次订货.下面以一个订货周期内库存系统的风险损失最小为目标建立模型.

图1　“之字形”不确定分布

3.1ξ

假定正常需求速度为R时的最优库存量为Q0，当ξ

R为需求速度时周期T内平均存贮量

则周期T内平均积压量为Q0-Q1， 积压增加的存贮费为

3.2ξ>R时的库存损失

周期T内平均库存节省费用

因此，当ξ>R时，周期T内综合损失费用为

图2　ξ>R时缺货库存

综上分析，需求速度为ξ时的风险损失函数为

3.3风险损失函数下订货周期和订货量的决策

图3　库存风险函数与需求量的可能性分布

在不确定分布Φ(ξ)下，风险函数R(ξ)与ξ轴围成面积的重心横坐标为

由假设(vi)知ξ服从Z(R1,R,R2)的之字形分布.根据不确定测度的性质及测度反演定理可知：

记α1=M{R1≤ξ≤R}，α2=M{R≤ξ≤R2},则

其中，

4仿真与灵敏度分析

有些时候库存问题中难以找到统计数据，现在根据Liu[2]建立的不确定理论的运算规律，依靠管理者的经验数据进行仿真和灵敏度分析.仿真计算结果见表1，参数C1,C2,C3对最优解的影响分别见表2、表3和表4.

表1　仿真计算结果

注：计算过程中取C1=1,C2=100,C3=2000,α1=0.3,α2=0.4.

表2　C1对最优解的影响

注：计算过程中取C2=100,C3=2000,R=100,R1=20,R2=150,α1=0.3,α2=0.4.

表3　C2对最优解的影响

注：计算过程中取C1=1,C3=2000,R=100,R1=20,R2=150,α1=0.3,α2=0.4.

表4　C3对最优解的影响

注：计算过程中取C1=1,C2=100,R=100,R1=20,R2=150,α1=0.3,α2=0.4.

从表1可以看到,修正后的订货周期小于等于经典订货周期，修正后的经济订货批量大于经典经济订货批量，随着需求量的增加订货周期缩短，订货量增加.由表2可以看到,随着单位时间内单位物品存贮费的增加，修正后的经济订货批量与经典经济订货批量的基差越来越小，而修正后的订货周期与经典订货周期的基差无明显的一致性.由表3可以看到,随着单位时间内单位物品的缺货损失费的增加，修正后的经济订货批量和订货周期与经典经济订货批量和订货周期一致，无明显改变.由表4可以看到,随着订货商处理每笔订单的订货费的增加,修正后的经济订货批量大于经典经济订货批量，而且修正后的经济订货批量与经典经济订货批量的基差越来越大，修正后的订货周期与经典订货周期基本一致性．

5结论

本文对经典库存在需求发生变化时产生的损失进行讨论，针对需求变化带来的经济损失定义了风险函数.在给出需求变化的之字形不确定分布条件下，对传统的经济批量模型进行修正，得到了不确定意义下的库存风险规避方案，即通过求风险函数在之字形分布下的重心，用重心决策方法得出不确定需求下的最优存贮量，为库存控制最优策略问题的研究提供了一种方法.应用数学软件Matlab，通过数值仿真计算实际需求速度介于一旦发生变化后的最小可能需求速度和最大可能需求速度之间的最佳订货周期和最佳订货量，与经典库存模型的订货周期和订货量做了清晰的比较.通过对模型主要参数(C1,C2,C3)的灵敏度分析，显示出各主要参数的变化对最优解的影响程度.本文所建立的模型还可以做更深层次的研究，如考虑资金的时间价值、产品寿命周期、仓库容量有限等情况，显然这些假设条件会增加数学分析的难度，但却更符合实际情况.

参考文献:

[1]LIU B D.UncertaintyTheory[M].2nd ed.Berlin:Springer,2007.

[2]LIU B D.UncertaintyTheory:ABranchofMathematicsforModelingHumanUncertainty[M].Berlin:Springer,2010.

[3]LIU B D.Uncertain set theory and uncertaininference rule with application to uncertain control[J].JournalofUncertainSystems,2010,4(2):83.

[4]LIU B D.Membership functions and operational law of uncertion sets[J].FuzzyOptimizationandDecisionMaking,2012,11(4):387.

[5]ZADEH L A.Fuzzy sets[J].InformationandControl,1965,8:338.

[6]MATHERON G.RandomSetsandIntegralGeometry[M].New York:Wiley,1975.

[7]KOLMOGOROV A N.GrundbegriffederWahrscheinlichkeitsrechnungJulius[M].Berlin:Springer,1933.

[8]李温红.仓库容量有限条件下的不允许缺货存贮模型[J].系统工程理论方法应用,1997,6(3):68.

[9]宋国防,聂德怀,汪建辉.库容有限且有批量折扣的不允许缺货存贮模型[J].天津大学学报,1999,32(5):604.

[10]杨益民,付必胜.仓库容量有限条件下的生产销售存贮模型[J].系统工程,2001,19(1):18.

[11]罗兵,王晶晶,常旭华.存货影响销售和顾客等待的特价商品模型[J].系统工程学报,2013,28(3):362.

[12]万延花,陈伟达.需求不确定的再制造批量决策[J].系统管理学报,2012,21(2):270.

[13]ILKYEONG M,LEE S.The effects of inflation and time-value of money on an economic order quantity model with a random product life cycle[J].EuropeanJournalofOperationalResearch,2000,125:588.

[14]GUPTA R,VRAT P.Inventory model for stock-dependent consumption rate[J].OperationResearch,1986,23:19.

[15]PADMANABHAN G,VRAT P.EOQ models for perishable items under stock dependent selling rate[J].EuropeanJournalofOperationalResearch,1995,86:281.

[16]王道平,于俊娣,李向阳.需求和采购价格均为时变的易变质物品EOQ模型[J].数学的实践与认识,2011,41(8):59.

[17]冯颖,蔡小强,涂菶生.资金和库存空间约束下多种易变质产品的联合订购策略[J].兰州大学学报(自然科学版),2009,45(6):142.

[18]李明芳,王道平.延期支付期限与订货量相关情形下的EOQ模型[J].系统管理学报,2011,20(4):389.

[19]KACPR Y J,STANIEW K P.Long-term inventory policy-making through fuzzy decision-making models[J].FuzzySetsandSystems,1982,8:117.

[20]PARK K S.Fuzzy set theoretic interpretation of economic order quantity[J].IEEETransactionsonSystemsandCybernetics,1987(SMC-17):1082.

[21]LI S,KABADI S H,NAIR K P K.Fuzzy models for single-period inventory problem[J].FuzzySetsandSystems,2002,132：273.

[22]CHANG S C,YAO J S,LEE H M.Economic reorder point for fuzzy backorder quantity[J].EuropeanJournalofEuropeanJournalofOperationalResearch,1998,109(1):183.

[23]WU K M,YAO J S.Fuzzy inventory with backorder for fuzzy order quantity and fuzzy short age quantity[J].EuropeanJournalofOperationalResearch,2003,150(2):320.

[24]EYNAN A I,DEAN H K.Effective and simple EOQ- like solutions for stochastic demand periodic review systems[J].EuropeanJournalofOperationalResearch,2007,180(3):1135.

[25]GEUNES J P,RANGA V R,JACK C H.Adapting the newsvendor model for infinite-horizon inventory systems[J].InternationalJournalofProductionEconomics,2001,72(3):237.

[26]SHAO Zhen,JI Xiao-yu.Fuzzy multi-product constraint newsboy problem[J].AppliedMathematicsandComputation,2006,180(1):7.

[27]张福利,达庆利.不确定需求条件下制造商的退货政策[J].系统管理学报,2013,22(2):185.

[28]邱若臻,黄小原,苑红涛.需求分布不确定条件下的多周期库存鲁棒优化模型[J].控制与决策,2014,29(9):1645.

[29]程硕,张毕西,曹铭,等.需求不确定情况下的多周期生产批量决策[J].数学的实践与认识,2015,45(11):39.

[30]赵明,周永务.随机模糊需求下的自由分布报童问题研究[J].合肥工业大学学报(自然科学版),2011,34(6):932.

[31]赵建华,李薇,刘雅娜,等.不确定环境下投资收益与风险问题的模型研究[J].石家庄学院学报,2015,17(3):22.

(责任编辑马宇鸿)