GFRP管混凝土长柱轴压极限承载力研究

杨俊杰，杨　城

(浙江工业大学 建筑工程学院，浙江 杭州 310014)

GFRP管混凝土长柱轴压极限承载力研究

杨俊杰，杨城

(浙江工业大学 建筑工程学院，浙江 杭州 310014)

摘要：为了得到GFRP管混凝土组合长柱的轴压极限承载力计算方法，在对组合长柱的破坏特征进行分析的基础上，分别采用了钢管混凝土柱承载力计算模型和欧拉公式对GFRP套管长柱的承载力进行了探讨；总结了现有的GFRP混凝土组合短柱极限承载力的计算方法，并根据长柱的特点，引入了组合长柱承载力的稳定系数，通过对已有的组合长柱的承载力试验数据进行拟合分析，得到稳定系数与构件长径比间的线性关系，以此得到计算GFRP管混凝土长柱承载力的稳定系数法；最后通过试验比较了各方法的相对误差，其中采用稳定系数法计算的结果最为理想.

关键词：GFRP；组合长柱；承载力计算模型；轴压试验

Research on the bearing capacity of long GFRP-reinforced concrete

composite columns subjected to axial compression

YANG Junjie, YANG Cheng

(College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310014, China)

Abstract:Based on the analysis of the failure characteristics of long GFRP-reinforced concrete composite columns, the bearing capacity is discussed using the computational model for the bearing capacity of concrete filled steel tubular columns and the Euler formula, respectively, to present the computational method for the bearing capacity of long GFRP-reinforced concrete composite columns. The existing computational methods for the bearing capacity of short GFRP-reinforced concrete composite columns are summarized. According to the characteristics of long columns, a stability coefficient is introduced into the bearing capacity of long composite columns. Through regression analyses of the existing experimental data on the bearing capacity of long composite columns, a linear relationship between the stability coefficient and the column slenderness ratio is obtained. A stability coefficient formula is derived to calculate the bearing capacity of long GFRP-reinforced concrete composite columns. Finally, the relative errors given by various methods are compared, which indicates that the stability coefficient formula agrees best with test data.

Key words:GFRP; long composite column; computational model of bearing capacity; axial compression experiment

纤维增强复合材料(FRP)作为一种新型材料，因其具有轻质高强、耐高温、耐腐蚀、抗蠕变以及施工方便等特点，近年来开始广泛应用于建筑结构中.其中玻璃纤维增强复合材料(GFRP)多用于约束混凝土构件，将新拌混凝土浇筑到GFRP管中形成的新式混凝土组合柱，最先由研究员Amir mirmiran提出[1].目前针对GFRP管混凝土柱的研究大多局限于长细比较小的组合短柱[2-4]，关于组合中长柱的研究比较缺乏，而实际工程中还存在着大量长细比较大的柱子，如高桥墩、宾馆中厅柱等.中长柱在受轴向荷载作用时，可能在强度破坏前已发生失稳破坏.因此，已有的关于组合短柱的承载力计算公式并不适用于组合长柱.笔者在分析GFRP管混凝土长柱破坏特征的基础上，采用不同的计算模型来探讨组合长柱的极限承载力，并通过试验比较了各方法的精确性.

1GFRP管混凝土长柱轴压破坏特征

普通钢筋混凝土轴心受压长柱，其破坏特征表现为：破坏时，长柱凹侧首先出现纵向裂缝，之后混凝土被压碎，纵筋受压屈曲向外凸出；长柱凸侧混凝土产生垂直于纵轴方向的水平裂缝，侧向挠度迅速增大，随后柱子破坏.

文献[5]对钢管混凝土中长柱的轴压性能进行了试验研究，破坏过程表现：当构件将要达到临界荷载时，其侧向位移急剧增大，钢管发生侧弯后，纵向应变突然增大且远大于环向应变，使环向应变减小；达到最大承载力后，继续加载，内部核心混凝土发生剪切流动，钢管外表面发生局部屈曲并出现鼓包，承载能力持续下降，试件严重变形.

文献[6]对九根不同长细比的GFRP管混凝土长柱进行了轴压试验研究，加载过程中发现：长细比较大的构件在达到最大荷载后其荷载应变曲线出现下降段，挠曲变形大，压区的GFRP管首先达到极限应变而发生破坏，随后混凝土被压碎；随着长细比的继续增大，构件达到最大荷载后，其荷载下降更快，挠曲变形增加迅速，直至柱子发生失稳破坏时GFRP管尚未出现破坏.

总结现有的关于组合长柱的轴压试验研究可以发现，各种长柱的破坏特征均存在一定相似性，随着长细比的增大，构件逐渐由强度破坏转变为失稳破坏.GFRP套管柱与传统钢筋混凝土柱的区别之处在于，GFRP组合长柱达到极限承载力后，其峰值荷载下降的幅度远高于普通混凝土长柱.而GFRP套管与钢管对核心区混凝土的约束机理更为类似(图1)，两者均对内部混凝土提供侧向约束力而使其处于三向受压状态，从而提高其承载力.区别在于GFRP与钢管的物理力学性能参数不同，一般认为钢材为各向同性材料，而GFRP管由玻璃纤维按一定角度缠绕而成，严格意义上并非为均质材料，因此与核心混凝土的结合效应也会有所不同.

图1　内部混凝土和GFRP管(钢管)受力简图Fig.1　Force diagram of internal concrete and GFRP tube(steel tube)

2GFRP管混凝土组合长柱承载力分析

2.1套箍指标法

考虑到GFRP套管混凝土组合柱和钢管混凝土组合柱的工作机理相似，因此可以尝试采用现有的钢管混凝土柱承载力计算方法来计算GFRP套管柱的极限承载力.

根据规范[7]中给出的钢管混凝土柱的承载力设计公式，结合GFRP管材的特点和力学性能参数，可得到GFRP套管混凝土长柱的承载力计算式为

Nu=φ1φeN0

(1)

式中：φ1为考虑长细比对承载力影响的折减系数；φe为考虑偏心率对承载力影响的折减系数，轴压构件该值取1；N0为GFRP套管短柱承载力设计值.其计算为

(2)

(3)

式中：φ为套箍指标，φ=AffFRP/Acfc，fFRP为GFRP管环向抗拉强度，Af为GFRP管的横截面面积；D为GFRP管外径；le为柱的等效计算长度，le=μkl，l为柱的实际长度，μ为考虑柱端约束条件影响的计算长度系数，两端铰支时该值取1，k为考虑柱身弯矩分布梯度影响的等效长度系数，轴心受压构件该值取1；α,ξ为由混凝土强度等级确定的系数，对于C40强度的混凝土取值分别为2,1；fc为混凝土抗压强度设计值；Ac为核心混凝土的横截面面积.

2.2欧拉公式法

对于长细比较大的柱，可以假定破坏时出现了弹性失稳，即构件的破坏是由于弯曲导致的侧向挠度过大引起的，极限荷载可以试用欧拉公式确定：

(4)

EI=EcIc+EFRPIFRP

(5)

式中：Ec,Ic分别为混凝土柱的弹性模量和截面惯性矩；EFRP,IFRP分别为GFRP管的轴向弹性模量和截面惯性矩.

GFRP管为线弹性材料，其弹性模量为定值.而混凝土由于存在套管的约束，其应力应变曲线受到三向受压状态的影响，因此关键问题是确定混凝土在临界荷载时的切线模量.建议采用Samaan提出的FRP约束混凝土应力应变关系模型[8]：

(6)

式中：fc,εc分别为FRP约束混凝土的轴向应力与应变；E1,E2分别为混凝土应力应变曲线第一线性段和第二线性段的斜率；f0为第二线性段反向延长线与纵向应力轴的交点；n为与混凝土强度等级有关的过渡段控制参数，n值越小则过渡段的曲率半径越大(越平缓)，一般情况下n取值为1.3～1.8，低强混凝土建议取1.3，如图2所示.

图2　Samaan双线性模型Fig.2　Samaan bilinear model

式(6)中参数表达式如下：

(7)

(8)

f0=0.872fco+0.371fcon+6.258

(9)

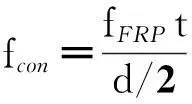
由于fc是关于εc的函数，且此函数连续光滑、处处可导，于是将fc对εc求导，可以得到任意位置的切线模量Ec为

(10)

因此，只要代入临界状态下的应变值εc，可以求得此时混凝土的切线模量，再将切线模量代入式(4，5)，便可求出组合柱的轴压极限荷载.

另外，根据强度公式，组合柱的轴压极限荷载还可以表示为

Nu=fcrAc

(11)

式中fcr为临界荷载下GFRP套管内混凝土的轴压应力，可以将临界应变值代入式(6)求出.临界状态下，式(4)应与式(11)相等.

于是，用欧拉公式法求组合柱承载力的步骤可以归纳为：先取一个初始应变值εc，分别代入式(6，10)，可以计算出轴压应力fcr和混凝土切线模量Ec；再将Ec和fcr分别代入式(4，11)，可以求出极限荷载Nu1和Nu2；比较Nu1和Nu2，如果两者相等，那么该值即为所求荷载，如果Nu1>Nu2，增大应变值εc，如果Nu1

2.3稳定系数法

2.3.1组合短柱承载力计算模型

目前，针对FRP约束混凝土短柱的承载力计算方法已有一定研究成果，总结现有的关于FRP混凝土组合短柱的极限承载力计算方法[4,9-11]，可归纳出计算模型如下：

N0=Acfcc+Afσf

(12)

fcc=fco+mfcon

(13)

式中：fcc为三向受压状态下GFRP管混凝土圆柱的核心混凝土轴心抗压强度；σf为GFRP管压应力，σf=EFRPεcu，εcu为混凝土极限压应变；m为侧向作用力提高系数，目前相关文献关于m的取值意见不一，且多数直接取一定值，而较小的m值误差都会造成组合柱极限承载力计算的不准确.

2.3.2侧向作用力提高系数m值的确定

由式(12，13)以及fcon和σf的计算式可以导出m的表达式为

(14)

通过对9根不同纤维铺设角度组合短柱的轴压试验，得到各构件的承载力值N0，将试验值及各物理参数代入式(14)，可以求出各构件对应的m值，见表1.表1中θ为GFRP管纤维铺设角度，fcu,k为混凝土立方体抗压强度.各试件尺寸相同.

表1　各试件材料参数及侧向作用力提高系数

可以看到：m值并不固定，其随纤维缠绕角度的增大而减小，且与混凝土强度等级关系不大.而纤维缠绕角度的影响主要体现着侧向约束力上，因此可对侧向约束力fcon和提高系数m进行拟合，得出两者间关系.

通过对侧向约束力和侧向作用力提高系数的简单拟合(图3)，可得到表达式如下：

(15)

图3　侧向约束力与提高系数之间关系Fig.3　Relationship between lateral force and improvement coefficient

2.3.3GFRP管混凝土组合长柱的稳定系数

根据已有的试验研究可以知道：随着长细比的增大，GFRP管约束混凝土柱的极限承载力逐渐减小，但针对组合长柱的稳定系数和长细比之间的定量关系却少有文献涉及.文献[6]对长径比为3至12不等共9根柱子进行了轴压试验，并以长径比为3的柱子作为比较对象，得到其余每根柱子的承载力降低幅度；文献[12]进行了3种径厚比和4种长径比(L/D为2，3，4，5)共24根GFRP管混凝土圆柱的轴压试验，并认为长径比大于2时承载力便开始有降低趋势；文献[13]进行了4种偏心距、2种长径比(L/D为8.4，20.4)共16根试件的试验，并将实测平均值与长径比为3的圆柱体试件测试值做了对比.收集了国内外已有的组合长柱试验数据[6,12-14]，并通过对这些数据进行回归分析(图4)，得出GFRP约束混凝土柱的极限承载力稳定系数φ与柱子的长径比L/D间的关系表达式为

(16)

可以看到：稳定系数与长径比之间大致呈线性关系，构件的长径比不大于3时即认为是短柱，此时不考虑稳定系数对承载力的折减.

图4　稳定系数与柱子长径比之间关系Fig.4　Relationship between stability coefficient and slenderness ratio of columns

经过拟合得到的关系式的决定系数为0.962，和方差为0.032，可见拟合程度较为理想.

至此，由式(12,13,15,16)可以得到GFRP管混凝土中长柱(L/D>3)的极限承载力Nu的计算式为

(17)

2.4各计算方法误差比较

为了验证上述几种承载力计算模型的准确性，进行了GFRP管混凝土组合长柱的轴压试验.试件相关参数如表2所示.

表2　长柱试件相关参数

制作好的试件如图5所示，加载过程如图6所示.

图5　长柱试件Fig.5　Test specimen of long columns

图6　长柱加载Fig.6　Loading process of long columns

将极限承载力试验值以及各计算模型中的关键参数、计算结果及误差列于表3.为了增强试验验证的可信度，同时将文献[6]中的部分试验结果和计算结果也列于表3中.

由表3可以看到：采用稳定系数法算得的理论承载力最接近实际值，而且相对试验值略偏于安全，计算过程也比较简单直观.套箍指标法计算值略大于实际值，原因在于，套箍指标法中的套箍指标表达形式是基于钢管与混凝土之间的相互结合性能分析得出的，而GFRP管与钢管的材料力学性能存在差异，因此与混凝土的相互作用机理也会有所不同；并且其中的折减系数也是针对钢管柱试验值的归纳分析得出的，钢材的抗拉强度高，其折减系数随长细比的下降幅度要比GFRP套管柱小.用欧拉公式算得的承载力相对误差偏大，欧拉公式的应用前提是构件为弹性失稳，而GFRP套管柱的破坏特征较复杂，并非单一的弹性失稳，因此算得的承载力有一定误差，且算得的值偏于不安全，另外运用该方法计算时需要反复迭代，不便于工程设计应用.

表3　各公式计算结果与试验结果对比

3结论

GFRP套管混凝土柱随长细比的增大其破坏形式由强度破坏转变为失稳破坏，在分析其破坏特征

的基础上，对几种长柱承载力计算方法进行了分析比较；并归纳出GFRP套管长柱的稳定系数与柱子长径比之间的相互关系.再与长柱试验结果的比较可得：1) GFRP套管长柱的稳定系数与长径比之间近似呈线性关系；2) 采用稳定系数法计算GFRP套管长柱的轴压承载力与试验结果符合较好，且计算过程简单直观，因此GFRP套管长柱的承载力计算可直接应用短柱的计算模型，再乘以稳定系数即可.

参考文献：

[1]MIRMIRAN A. A new concrete filled hollow FRP composite column [J]. Composites,1996,27(B):263-268.

[2]秦国鹏,王连广.GFRP管混凝土组合柱轴压性能研究[J].工业建筑,2009,39(10):72-75.

[3]杨俊杰,周涛.纤维铺设角度对FRP-混凝土组合柱承载力影响的有限元分析[J].浙江工业大学学报,2014,42(2):294-297.

[4]曾向往.FRP管的力学计算及FRP管混凝土轴压构件研究[D].武汉:华中科技大学,2013.

[5]王力尚,钱稼茹.钢管高强混凝土柱轴向受压承载力试验研究[J].建筑结构,2003,33(7):46-49.

[6]王清湘.GFRP套管混凝土长柱轴压力学性能试验[J].建筑结构,2010,40(11):80-83.

[7]中华人民共和国住房和城乡建设部.GB 50936—2014钢管混凝土结构技术规范[S].北京：中国建筑工业出版社,2014.

[8]SAMAAN M, MIRMIRAN A. Model of concrete confined fiber composite[J]. Journal of Structural Engineering，1998,124(9):1025-1031.

[9]周乐.FRP高强混凝土轴压力学性能研究[J].沈阳建筑大学学报,2009,25(1):121-124.

[10]LAM L, TENG J G. Strength models for fiber-reinforced plastic-confined concrete[J]. Journal of Structural Engineering,2002,128(5):612-623.

[11]常占宏.FRP混凝土轴压短柱的极限承载力研究[J].上海公路,2009(2):48-49.

[12]MIRMIRAN A, SHAHAWY M, SAMAAN M. Effect of column parameters on FRP-confined concrete[J]. Journal of Composites for Construction,1998,2(4):175-185.

[13]陶忠,于清,韩林海,等.FRP约束钢筋混凝土圆柱力学性能的试验研究[J].建筑结构学报,2004,25(6):75-82.

[14]MIRMIRAN A, SHAHAWY M, BEITLEMAN T. Slenderness limit for hybrid FRP-concrete column[J]. Journal of Composites for Construction,2001,5(1):26-34.

(责任编辑：陈石平)

文章编号：1006-4303(2015)06-0685-05

中图分类号：TU398+.9

文献标志码：A

作者简介：杨俊杰(1958—)，男，浙江诸暨人，教授，研究方向为钢筋混凝土结构，E-mail: 1095129199@qq.com.

收稿日期：2015-05-06