接触式螺纹测量仪的六自由度位姿误差的测量与补偿
,,,
(1.南京航空航天大学,江苏 南京 210016;2.南京紫金计量有限公司,江苏 南京 210028)
Measurement and Compensation of Pose Errors of Contact MeasuringInstrument of Screw Thread Parameter
ZHU Hehe1 ,ZHAO Dongbiao1 ,SHEN Jianqing2 ,GONG Guoyun2
(1. Nanjing University of Aeronautics and Astronautics, Nanjing 210016,China;2. Nanjing Zijin Measurement Co.,
Ltd, Nanjing 210028,China)
摘要:为了提高接触式螺纹测量仪的测量精度,通过深入的误差分析,提出了针对高精度接触式螺纹测量仪的六自由度位姿误差的一种新的误差测量和补偿的方法。设计了一套适用于螺纹测量仪的标准规,用于综合测量探针相对于螺纹专用夹具的六自由度位姿误差。利用参数已知的精密标准规代替参数未知的被测螺纹进行扫描测量,建立螺纹测量仪的误差综合测量方程组,并代入受六自由度位姿误差影响的扫描数据,解方程组反求出探针运动空间的六自由度位姿误差,然后,在不更换探针和专用夹具的情况下,对被测螺纹进行扫描测量,建立螺纹测量仪的误差补偿方程组,并将综合误差测量所得的相关误差参数带入方程组,求解出被测螺纹的理想轮廓信息,完成高精度接触式螺纹测量仪的综合误差补偿。
关键词:接触式螺纹测量仪;误差测量;误差补偿
接触式螺纹测量仪的六自由度位姿误差的测量与补偿
朱贺贺1,赵东标1,沈建清2,贡国云2
(1.南京航空航天大学,江苏 南京 210016;2.南京紫金计量有限公司,江苏 南京 210028)
Measurement and Compensation of Pose Errors of Contact MeasuringInstrument of Screw Thread Parameter
ZHU Hehe1,ZHAO Dongbiao1,SHEN Jianqing2,GONG Guoyun2
(1. Nanjing University of Aeronautics and Astronautics, Nanjing 210016,China;2. Nanjing Zijin Measurement Co.,
Ltd, Nanjing 210028,China)

摘要:为了提高接触式螺纹测量仪的测量精度,通过深入的误差分析,提出了针对高精度接触式螺纹测量仪的六自由度位姿误差的一种新的误差测量和补偿的方法。设计了一套适用于螺纹测量仪的标准规,用于综合测量探针相对于螺纹专用夹具的六自由度位姿误差。利用参数已知的精密标准规代替参数未知的被测螺纹进行扫描测量,建立螺纹测量仪的误差综合测量方程组,并代入受六自由度位姿误差影响的扫描数据,解方程组反求出探针运动空间的六自由度位姿误差,然后,在不更换探针和专用夹具的情况下,对被测螺纹进行扫描测量,建立螺纹测量仪的误差补偿方程组,并将综合误差测量所得的相关误差参数带入方程组,求解出被测螺纹的理想轮廓信息,完成高精度接触式螺纹测量仪的综合误差补偿。
关键词:接触式螺纹测量仪;误差测量;误差补偿
收稿日期:2014-12-19
中图分类号:TP273
文献标识码:A
文章编号:1001-2257(2015)03-0058-04
Abstract:In order to improve the measuring accuracy of contact measuring instrument of screw thread parameter, a new method of measurement and compensation of pose errors is presented in this paper after error analysis. A new type of master gauge has been designed in this paper for measuring the six degrees of freedom comprehensive pose error between the measurement probe and the special fixture. At first, the master gauge whose parameters are known is measured by this instrument. The equations describing the relation between the parameters and the collected data of the mater gauge are built. The collected data which is affected by the pose errors is plugged into the equations. The pose errors can be obtained by solving the equations. Then, the screw thread is measured by this instrument without replacing the probe or the fixture. The pose errors obtained by errors measurement is plugged into the error compensation equation which is built in this paper. The wanted thread axis profile section obtained by solving the equations can be used to calculate the precise parameters of screw thread.
作者简介:朱贺贺(1989-),男,江苏徐州人,硕士研究生,研究方向为机电一体化、智能检测与控制;赵东标(1963-),男,安徽蚌埠人,教授、博士研究生导师,研究方向为数控技术、机器人技术、机器智能、微机电系统与微细制造。
Key words:contact measuring instrument of screw thread parameter;errors measurement;errors compensation
0引言
螺纹在机械设计与制造领域一直是使用最为广泛的。对螺纹多参数的精密检测更是一个世界性难题。遗憾的是中国的螺纹紧固件出口虽然位于世界第一, 但是螺纹零件的生产质量、检测水平和发达国家相比,还存有一定差距。所以研究快速、 高效、自动化、 人为因素影响低、精度高的螺纹测量方法和测量设备具有重大意义。为了满足螺纹高精度测量, 同时适量放宽高精度接触式螺纹检测仪的设计, 加工, 装配的苛刻要求, 提高经济性, 深入分析高精度接触式螺纹检测仪的误差及误差补偿就显得尤其重要。
1误差分析
接触式螺纹测量仪运动原理如图1所示。

图1 接触式螺纹测量仪运动原理
由图1可知,高精度接触式螺纹测量仪是一种非典型的二维运动平台,有X轴和Z轴2项直线运动和探针绕Y轴的转动。
在理想的情况下,探针的运动空间应该是与机床坐标系的XOZ面平行的一个平面,然而由于误差和变形的存在,不仅会使此平面产生6个自由度位姿变化,而且会使探针的运动空间从一个平面变成一个近似于平面的复杂曲面如图2所示。对这样的复杂曲面进行误差补偿困难极大。必须进行合理的简化以降低工程实现的难度。探针工作时的运动空间仅仅是上下2个狭长的运动空间平面,并且这2个平面不重合。这样的探针运动空间平面的平面度误差与六自由度的位姿误差相比是很小的,误差补偿策略流程如图3所示。

图2 探针运动空间的平面度

图3 几何误差的补偿策略
精度分配可保证探针运动平面的平面度要求,及在满足精度要求的情况下,可将探针运动空间化简为平面。 此平面与机床坐标系仅存在六自由度的位姿变化。螺纹被测件放置在专用夹具上,理想情况下,螺纹的中心线应与机床坐标系的X轴平行且与探针运动运动平面重合,同样,专用夹具的定位误差也会使被测螺纹产生6个自由度位姿误差。
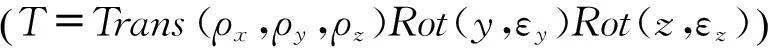
高精度接触式螺纹测量仪的探针为T型结构,探针的上下2个测尖均呈半圆球状,探针的尺寸根据被测螺纹的尺寸的不同而分成大中小3种。螺纹测量仪的测量系统采集的数据,经过运算只可以求得上下测尖球心的坐标,若要得到轮廓扫描点的坐标还需进行半径补偿。测尖半球与测量面的接触点与两者的相对位姿及被测面的轮廓有关。理想的情况下,测尖半径补偿可以看作XOZ面上的二维半径补偿。而实际情况下,由于螺纹测量仪误差和螺纹专用夹具误差的存在,使得探针和螺纹被测件相对位姿产生了变化。测尖半径补偿就由二维补偿变为三维补偿,复杂程度也加大了。
2六自由度综合误差间接测量
设计一种带有刻线的量块作为校准规,其截面为b×b正方形,并且经过精密的加工和准确的测量,如图4所示。

图4 量块校准规
通过采集参数已知的量块上点坐标,建立相关方程组,反求齐次坐标变换矩阵,借此完成综合误差的间接测量,即获取精密加工的标准规的精密参数;用螺纹检测仪对标准规进行扫描测量;利用标准规自身参数以及扫描测量数据的关系联立方程组;求解方程组解出六自由度误差变换矩阵。
由几何学推导出的量规与探针运动空间平面的交线可表示为:

(1)
T=Trans(ρx,ρy,ρz)Rot(x,εx)Rot(x,εx)Rot(z,εz)为探针运动空间平面与被测螺纹的六自由度相对位姿的齐次变换误差矩阵。(X,Y,Z)是在工件坐标系下的标准规表面点坐标,其参数描述方程为:
(2)
由实际测量得到的量块与探针运动空间平面的交线可表示为:
(3)
(XS,0,ZS)为测量仪采集的测尖球心运动轨迹拟合的直线段的坐标,OB指测尖球心到过球心垂直线与被测面交点的距离。其推导过程为:
y≥0,z≥0
y<0,z≥0
y≥0,z<0
y<0,z<0
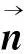
r为探针的测尖半径;φ为OA与OB的夹角。则OB的最终表达式为:
(4)
联立式(1),式(3)可得:
(5)
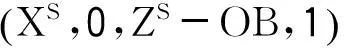

图5 上下扫描线共有四种不同形式
出于方便计算的考虑,将式(5)离散化处理得:
(6)
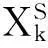
3误差补偿
利用标准规求出齐次坐标变换矩阵,那么就确定了探针运动空间平面和螺纹专用夹具的相对位姿误差T。在不更换探针和螺纹专用夹具,即探针运动空间平面和螺纹专用夹具的相对位姿不发生改变的情况下,对螺纹被测件进行测量。可以认为六自由度齐次误差矩阵不发生变化。螺纹的轮廓较复杂,螺纹牙顶、牙底、左右牙侧补偿略有不同,应分别补偿。通过对采集的数据进行分析,可以对螺纹牙顶、牙底及左右牙侧进行辨识。
实际加工的螺纹牙顶,牙底,左右牙侧在相对狭窄的扫描范围可视为由微小圆柱面积分而成,则描述螺纹轮廓的参数方程为:
(7)
与式(6)同理可得牙顶或牙底的方程组为:
(8)
此处的OB推导过程为:
因此,式(8)可表示为:
(9)

图6 测尖半径补偿的微元分割
综上所述,式(9)可变为:
(10)
方程组(10)中未知数个数和方程个数都是3个,方程变为可解。
牙侧补偿与牙顶、牙底补偿不同,必须考虑牙侧角β的影响。
右牙侧补偿的OB推导过程为:
(cosβ,sinφ,cosφ·sinβ,1)T

则OBk=g(φk,β)=g(θk,β)。
式(10)可变为:
(11)
同理,左牙侧补偿的推导过程为:
(-cosβ,sinφ,cosφ·sinβ,1)T


式(10)可变形为:
(12)
对方程组进行求解,解出的xk,Rk正是螺纹被测件关于工件坐标系的真实轮廓数据,利用这些数据就可以对螺纹多个参数进行精确计算。
4结束语
为了满足螺纹测量仪的测量精度的要求,在此,经过深入的误差分析空间综合误差螺纹测量仪的特点,提出了着重补偿六自由度位姿误差的策略,并描述了六自由度位姿综合误差测量方法和误差补偿方法。该方法操作简便,不需要多种昂贵的测量仪器,工程实现的难度不大且具有好的经济性。其应用可扩展到其他具有二维运动结构的机床或测量仪,具有一定的通用性。
参考文献:
[1]Zhang H, Katz R, Agapiou J S. Inprocess inspection of internal threads of machined automotive parts //SPIE Optical Engineering Applications. International Society for Optics and Photonics, 2009:74320D-74320D-9.
[2]Kang F,Fan J W. A method for manufacturing accuracy distribution and optimization of a CNC machine tool .Mechanical Science and Technology for Aerospace Engineering, 2008, 27(5):588-591.
[3]Chen S, Zhao D, Lu Y, et al. A method for detecting alignment deviation on a thread- measuring instrument . Measurement Science and Technology, 2013, 24(8):1-9.
[4]Okafor A C, Ertekin Y M.Derivation of machine tool error models and error compensa- tion procedure for three axes vertical machining center using rigid body kinematics . International Journal of Machine Tools and Manufacturing. 2000(40):1199-1213.
[5]Zhu S, Ding G, Qin S, et al. Integrated geometric error modeling, identification and compensation of CNC machine tools . International Journal of Machine Tools and Manufacture, 2012, 52(1):24-29.
[6]Wang H M. Compensation technology and application for probe radius of coordinate measuring machine .Technology and Test, 2010( 6):109-115.
[7]Menq C, Chen F L.Curve and surface approximation from CMM measurement data . Computer and Industry Engineering, 1996, 30(2):211-215.

