一种基于遗传算法的NCS控制器延时约束参数优化方法
,,
(贵州大学电气工程学院,贵州 贵阳 550025)
An Optimized Method of Time-delay Constraint Parameter ofNCS Controller Based on Genetic Algorithm
ZHANG He,WANG Honglei,LI Na
(The Electrical Engineering College, Guizhou University,Guiyang 550025,China)
一种基于遗传算法的NCS控制器延时约束参数优化方法
张赫,王红蕾,李娜
(贵州大学电气工程学院,贵州 贵阳 550025)
An Optimized Method of Time-delay Constraint Parameter ofNCS Controller Based on Genetic Algorithm
ZHANG He,WANG Honglei,LI Na
(The Electrical Engineering College, Guizhou University,Guiyang 550025,China)
摘要:网络化控制系统(NCS)设计中,如何提高系统性能质量(QOP)及网络服务质量(QOS)一直是本领域的热点问题,而对于此类问题的寻优过程必然需要以网络系统的数据延迟以及丢包问题展开。针对此问题,提出了一种基于遗传算法的网络化控制系统闭环延迟约束参数优化方法。在保证系统稳定性的情况下提高控制质量。最后给出了一组仿真参数,验证了方法的可行性与有效性。
关键词:网络化控制系统;QOP;QOS;遗传算法;闭环延时参数
中图分类号:TP202;TP393
文献标识码:A
文章编号:1001-2257(2015)03-0054-04
收稿日期:2014-12-04
Abstract:How to improve the quality of performance(hereafter called QOP) and the quality of service(hereafter called QOS) in the design of networked control systems (hereafter called NCS) has been the hotspot in the field of NCS, but few achievements in the current study mentioned the coordination design method of the two. Aiming at this problem, To improve the quality of network service on the basis of guarantee the QOP, in this paper a genetic algorithm based optimal design method about the parameter of Closed-loop delay time is proposed after the analysis and summary about some recent research results. Finally a simulation example is given to verify the feasibility and effectiveness of the method.
作者简介:张赫(1989-),男,山东临沂人,硕士研究生,研究方向为网络化控制及其应用;王红蕾(1959-),男,北京人,教授,博士研究生导师,博士研究方向为网络技术在控制系统中的应用、管理系统工程;李娜(1990-),女,山东济宁人,硕士研究生,研究方向为控制理论及其应用。

Key words:network control system; QOP; QOS; genetic algorithm; closed-loop delay parameter
0引言
网络化控制系统(NCS)是伴随计算机技术及自动控制技术的发展产生的,它将分布于不同未知的控制器,传感器,执行器通过数据通信网络连接形成闭环回路,网络化控制系统存在许多自身优点,如数据共享,远程操作与控制,以及减少点对点线路铺设等。目前,网络化控制系统仍然是控制领域的研究热点。但是,在带来许多优点的同时,由于数据传输信道的共享,网络化控制也面临着许多问题,如传输延时问题和丢包问题等。此类问题的出现降低了系统的控制质量也使得网络服务质量(QOS)下降。因此,一个实际的NCS中其网络的服务承载能力是一定的,在资源可调度的情况下,有效地分配资源可以减小延时时间,保证控制质量,同时采用合理的调度策略能够使网络负载在最佳状态以提高网络QOS。
针对网络化系统设计问题,有很多学者在此领域进行过研究[1CD*27]。在其研究中比较全面地阐述了针对多种数据的调度算法,提高了通信质量,然而是建立在针对源数据采集量已知的基础上优化调度,没有提及在设计时的延时约束问题。
针对上述研究总结,先前的研究多是针对确定系统来优化网络资源的调度,提及综合设计的多是近似的优化处理,无法明确的给出多个控制器闭环延时的优化设计。在此,提出一种结合遗传算法的NCS控制器设计策略,通过网络的最佳负载要求采用遗传算法寻优各个回路闭环延迟约束时间并以此为约束进行控制器设计,在保证控制系统控制质量的前提下尽可能充分利用网络资源,提升网络的QOS。
1NCS控制系统控制器设计
网络化控制系统回路由控制器和远端控制节点组成,远端节点又包括执行器,传感器和被控对象3个机构,被控对象由传感器采集信息后发送给远端控制器机构处理后得到控制指令,再由通信网络传递给执行机构进行控制,将远端机构视为1个节点处理就会得到一个由主控制节点和多个分布节点组成的网络化控制系统模型,如图1所示。多个节点对象共同组成控制系统,由于通信网络的共享,大量数据传输时一定会存在延时问题,考虑到相比于网络延时,节点上执行的延时非常小,因此,忽略由执行、计算带来的延时。多数据传输时数据的延时分为2个部分,以回路i为例,一是由控制对象传输实时数据到达控制器的延时τ1,另一个是控制信号由控制器到执行机构的传输延时τ2,共同组成一次控制的总延时τ=τ1+τ2。控制回路的质量直接依赖于闭环传输延时,因此,延时的大小直接决定着整个NCS控制系统的控制质量,同时延时的存在同样使得网络化服务质量QOS降低,系统设计时应尽可能避免延时产生。针对此问题,许多学者曾提出过关于保证稳定条件下确定闭环延迟的上限的方法,如采用矩阵不等式等相关理论确定方法等。
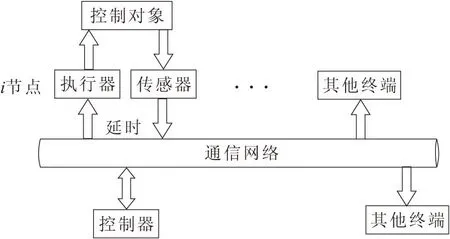
图1 网络化控制系统
当排队等待信号序列超出限制区域长度时,会引起数据包丢失问题,数据包丢失会使得延时在原有基础上增加固定周期的整数倍,T=τ+kTi。k为丢失数据包的个数,为更清楚的说明丢包对闭环控制的影响,其设计如图2所示。无论是从传感器到控制器的采样数据包丢失,还是控制器到执行器的控制数据包丢失,都会使执行机构的执行延时增加Ti。丢包问题的出现严重影响控制系统的QOS,在实际控制控制系统设计时就应避免丢包的出现。另外多包传输问题同样会增加系统的负担,由于传输通道的共享,多包传输问题会使得传输数据增加,导致通道阻塞甚至丢失数据,从而使得控制数据缺失,导致控制失真。
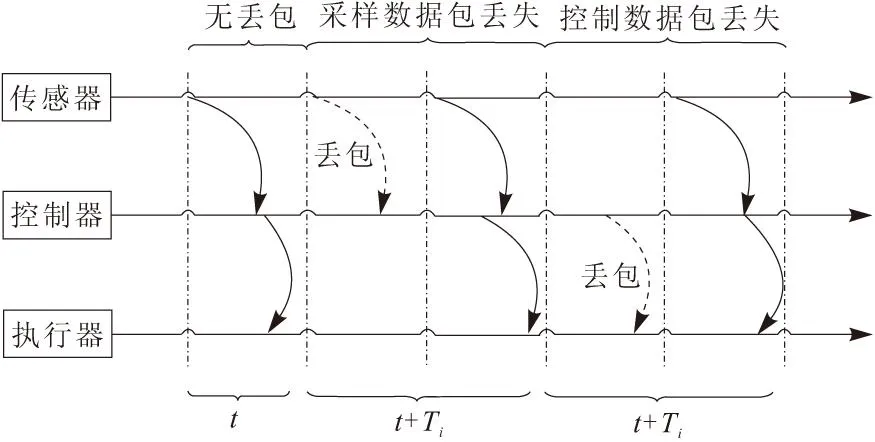
图2 数据包丢失引起的控制延时
在实际的NCS中由于众多节点的存在以及网络的共享使得在有限网络传输条件下必定会存在一个最佳负载点。在此点时,网络的总体利用率和网络QOS会达到最优,因此,在设计时满足控制对象要求下,合理设计控制器的闭环延迟上限将会提高整个NCS的性能。
针对上述分析,考虑在网络负载能力一定的情况下,引入遗传算法对多个对象进行控制器的闭环延迟约束时间进行优化训练,使得最终设计不但满足控制质量同时,还能最大程度的满足网络QOS。
2NCS控制器闭环延时约束优化
遗传算法作为一种优化算法,在针对多个对象参数优化方面具有很大的优势,其追寻的是整个种群的优化,因此,在具有多个对象节点的网络化控制系统中引入此算法是可行的,而且,遗传算法的鲁棒特性和其简单的操作规则也令其应用更加方便。在此,采用遗传算法优化控制器闭环延时设计上限。
假定在需设计的NCS中,所有数据包传输方式均为单包传输,则在一个具有N个控制对象(U1,U2……Un)的NCS中,每个控制器的闭环延迟约束τi必须服从如下变化范围,即


τ1为单个数据包的传输时间,由于采用的数据包长度为定值l,故其值为定值;Ti代表回路i的采样周期,2个参数表征闭环延迟约束的时间约束。而网络的负载以及控制的质量正是需要对闭环延迟τi的设计,因此,遗传算法需要优化的对象[τ1,τ2,τ3…τi…τN]。
根据对象特点为满足网络科调度条件,在编码时应以一个数据包传输的基本时间作为单位进行编码。在此,选用适用于多个对象训练的浮点型编码方式。应用的基本流程如图3所示。

图3 应用基本流程
由图3可以看出,遗传算法的给出需要定义适应度函数作为优化标准,根据设计目的,当闭环延时约束时间设计合适时,NCS在保证控制质量的前提下,可以使网络在最佳负载状态,在训练参数范围给定时已经保证了最终的设计不会超出控制质量限制,因此,可以根据训练参数带来的负载与网络最佳负载吻合度定义适应度函数。
参考文献根据中的相关公式可以总结得出,在数据包长度一定的网络环境下,实际负载可表示为: 参数优化结束,采用中提出的线性二次离散设计方法进行各控制器设计,并且在网络调度时,依照各回路的闭环延时约束指导各节点带宽分配规则,这样就使得保证性能质量的前提下,整个系统的运行维持在较高质量的服务下。另外,当系统中部分节点需要较高的控制要求时,可以再训练之初缩小其训练范围,以保证该节点的训练结果处于要求范围。
N为控制节点的个数;τi即为对应控制器闭环延时约束。显然,一个NCS中,实际负载小于网络最大承载量时系统才是可调度的[9CD*212]。在一个设计之初,网络的负载能力是一定的,最佳负载量B也可以根据总负载量给出。因此,根据上述描述,适应度函数可以表示为:
在此适应度函数下,网络的闭环延迟参数训练以寻求适应度函数的最小值为目标。显然,在训练之初,当各回路均采用所提供的最大延时上限仍不能满足网络负载条件时表明,各节点的控制要求在网络承受范围之外,此时,参数的训练没有实际意义,应当改变节点控制要求或者网络初始条件,在此只考虑一般情况下的设计问题。
另外遗传算法的完成过程中需要对种群变量进行选择,交叉,变异的操作,即
a.选择。在此采用联赛选择法,新种群产生后随机选择K个个体进行比较,选择最优个体进入下一代。参与选择的个体放回父代,如此反复,直到产生N个个体。
b.交叉。选择均与交叉方式,每个父代基因等概率的参与交叉运算,每一代中交叉的概率为Pr。
c.变异。为了使搜索在整个空间内移动,并且增加基因的多样性,在此选择均匀变异,从父代中随机选择K个个体,随机选择某个基因进行一定范围的随机值替换,选择的概率PB事先给出。
完成上述定义后,给出初始种群的数量N,以及终止迭代条件(最大迭代次数和适应度函数目标),最后设定相关操作概率后按照图3进行迭代,即可得到每个控制器闭环延迟约束。基于遗传算法的NCS控制器设计流程为:
a.给定网络初始条件,确定网络最佳负载B。
b.根据网络控制节点的采样时间限制,确定各个节点闭环延迟约束的范围(τi,Ti)。
c.判断网络性能是否满足最差延迟时间要求,如果不能满足,进行初始条件的重新协调,如改变给定网络条件,降低控制要求等。
d.在网络条件满足整定要求的情况下,依照网络最佳负载(取网络带宽的80%)对个控制闭环延迟约束时间进行遗传算法整定。训练时,各参数的变化应当以单包传输时间为基本时间单位,得出每个控制器的闭环延迟约束(τ1,τ2,τ3…τi…τN)。
e.按照整定参数指导每个控制器的设计,同时指导网络的调度。此时,网络产生的信息量,即为此网络条件下的最佳负载信息量。
3数字实例
为验证所提方法的实用性,在此,给出一个针对10个被控对象节点的NCS优化实例,同样在参数优化时忽略由执行计算带来的延时部分,针对10个被控对象,需要进行(τ1,τ2……τ10)的优化,根据系统条件,每个回路限制采样时间(s)不得超过(0.05,0.05,0.055,0.06,0.065,0.07,0.07,0.09,0.1,0.12)。所仿真的网络参数模型如表1所示。

表1 仿真网络参数模型
对系统10项闭环延时约束进行合理范围内的优化训练,时间最小取值为0.001 s,以此为时间单位经遗传算法训练,在遗传算法中给定初始种群数为10,最大迭代次数为100次,交叉概率Pr设定为0.85,变异概率PB设定为0.07。按照前述流程进行迭代。运算截止后得出控制器闭环延时约束条件如表2所示。

表2 遗传算法优化仿真结果

4结束语
继DCS,FCS之后NCS成为工控领域又一个新的研究热点,虽然目前在NCS方面的研究大多基于理论层面,但是相信,其应用在不久的将来一定会普及。同时,需要认识到的是NCS在带来数据共享和控制灵活等方面优势的同时也伴随着许多像控制延时,数据拥塞这样的问题,尤其是快速发展的在无线网络中,由于通信条件的限制,丢包问题和能量损耗问题等[13]尤为严重。此外,在该领域中,高级算法的应用很少涉及[14],因此,提出了基于遗传算法的控制器延时参数优化算法。但是,该方法在一定程度协调了网络控制质量与服务质量的同时也存在着许多问题,如通过该算法优化只能得到一组参数,但是实际系统中可能存在多组最优解等。另外,在其他学者成果的基础上理论性地提出了一种优化方法,仿真结果表明,网络工作时处于最佳负载附近。
[1]Zhang W, Branickym S, Philips S M. Stability of networked control system . IEEE Control Systems Magazine, 2001, 21(1): 84- 99.
[2]康军,戴冠中. 网络化控制系统综合控制方法研究. 控制与决策, 2009,24(2):181-186.
[3]彭晨,岳东. 网络环境下基于网络QoS 的网络控制器优化设计. 自动化学报, 2007,2(33): 214-217.
[4]Hong Seong Park. Scheduling algorithm of data sampling times in the integrated communication and control systems . IEEE Trans on Control System Technology, 1995,3(2): 225- 231.
[5]Hong Seong Park, Yu Chul Kim. Bandwidth allocation scheme in CAN protocol . IEEE Proceedings-Control Theory and Applications, 2000, 147(1): 37- 44.
[6]Hong Seong Park. Bandwidth allocation scheme for cyclic- service fieldbus networks . IEEE Trans on Mechatronics, 2001, 6(2): 197- 204.
[7]Hong Seong Park, Yu Chul Kim. Implementation of a bandwidth allocation scheme in a to ken- passing fieldbus network . IEEE Trans on Instrumentation and Measurement, 2002,51(2): 246- 251.
[8]Dong- Sung Kim, Young Sam Lee, Wook Hyun Kwon, et al. Maximum allowable delay bounds of networked control systems . Control Engineering Practice, 2003,11(11): 1301- 1313.
[9]白涛,吴智铭,杨根科. 网络化控制系统带宽配置的一种新策略. 自动化学报, 2004,30( 6) : 961- 967.
[10]Tipsuwan Y, Chow M Y. Network- based controller adaptation for network QoS negotiation and deterioration//Proc of the 27th Annual Conf of IEEE Industrial Electronics Society. Denver: IEEE Press, 2001: 1794- 1799.
[11]Chow M Y, Tipsuwan Y. Gain adaptation of networked DC motor controllers based on QOS variations . IEEE Trans on Industrial Electronic, 2003,50(5): 936- 943.
[12]Chow M Y, Tipsuwan Y. Network- based control system: A tutorial//Proc of the 27th Annual Conf of IEEE Industrial Electronics Society. Denver: IEEE Press, 2001: 257-261.
[13]Shuanglong Xie, Kay Soon Low, An Adaptive Tuning Algorithm based Network Control System. IEEE Ninth International Conference on ISSNIP, 2014:1-6.
[14]王雪艳. 网络控制系统的控制器设计方法概述. 系统仿真技术, 2010,6(1),53-58.

