基于灰类敏感度系数的评价指标客观权重极大熵配置模型

基于灰类敏感度系数的评价指标客观权重极大熵配置模型

刘红旗1～3，方志耕1，2李维东1，2陶良彦1，2

(1.南京航空航天大学经济与管理学院，江苏南京210016；2.南京航空航天大学科学发展研究中心;3.南京航空航天大学纪委办)

摘要：评价指标权重的确定是多属性决策问题中至关重要的环节。然而，既有研究利用评价指标值之间的差异性进行指标的客观赋权，往往忽略了评价指标对被评价对象全体及所在系统的重要性。本文基于事物自然本质属性差异，运用灰色关联聚类将评价对象划分到预设的类别；借鉴有无对比分析法的思想，定义了反映指标对全体被评价对象类别影响程度的灰类敏感度系数；根据极大熵准则，建立了基于灰类敏感度系数的客观权重极大熵配置模型，以确定多属性决策指标的权重。并通过与文献[21,26]中实际案例的对比分析，说明了本模型的有效性与更贴近现实性，为解决多属性决策指标客观赋权问题提出了一个新思路。

关键词：多属性决策;灰色关联聚类;灰类敏感度系数;极大熵;指标权重

收稿日期：2013-12-17

基金项目：国家自然科学基金资助项目(70971064,71173106,71171113)；国家社科基金重大项目(10zd&014)；国家社科基金重点项目(12AZD102)；教育部人文社科青年基金项目(12YJC630115,12YJC630276)；中央高校基本科研业务费专项科研项目资助(NJ20130021,NJ20140032)；江苏高校哲学社会科学重点研究基地重大项目(2010JDXM014,2010JDXM015,2012JDXM003)

作者简介：刘红旗(1981-),男，博士研究生，纪委办主任，助理研究员，研究方向:灰色系统理论、评价理论与方法；方志耕(1962-)，男，教授，博导，主要从事灰色系统、复杂装备研制与管理、质量管理等研究；李维东(1988- )，男，硕士，专业: 统计学，方向：质量管理；陶良彦(1988- ), 男，硕士，专业: 管理科学与工程，方向:复杂装备研制。

中图分类号：C934文章标识码：A

The Maximum Entropy Configuration Model of Objective Index Weight

Based on Grey Class Sensitivity Coefficient

LIU Hong-qi1～3， FANG Zhi-geng1，2, LI Wei-dong1，2, TAO Liang-yan1，2

(1.CollegeofEconomicsandManagement,NanjingUniversityofAeronauticsandAstronautics，Nanjing210016,China; 2.ScientificDevelopmentResearchCenter,NanjingUniversityofAeronauticsandAstronautics; 3.DisciplineInspectionCommissionOffice,NanjingUniversityofAeronauticsandAstronautics)

Abstract:To determine the weight values of assessment indexes is the crucial link in multiple attribute decision making problems. However, today’s researches have used the evaluation index difference, which tends to ignore the evaluation index of the importance for the evaluation object and the system. Based on the natural essence attribute differences, this article uses the grey correlation clustering to classify the evaluation object into the default category, and by the analysis method of being with or without contrast, defines the grey class sensitivity coefficient which influences the impact of the indexes for the evaluation of all the object classes; and based on the maximum entropy criterion，sets up the objective weight maximum entropy configuration model based on the grey class sensitivity coefficient to determine the weight of multiple attribute decision making. Through the contrast analysis of actual cases in ref. [21,26], it shows the effectiveness and closeness to the reality of this model, which has put forward a new thought for solving multiple attribute decision making problem.

Key words:multiple attribute decision making; grey correlation clustering; grey class sensitivity coefficient; maximum entropy; objective index weight

0引言

在多属性决策领域，人们要做出一项正确决策往往要综合考虑诸多影响因素，需要以多个属性为准则来构建决策评价指标体系，进行客观、全面、系统的综合评价。决策评价的结果取决于两个因素：一是评价指标的选择，二是指标权重的确定。指标权重的确定是否客观、合理，直接关系到能否把握住评价的标准和重点，直接影响到决策的准确性和科学性。评价指标权重是指标在整体评价系统中相对重要程度的表征。判断一组指标权重的合理与否并不能根据其是采用主观赋权还是客观赋权，而应该看其是否准确反映了评价指标对评价对象全体及所在系统的真实重要性。目前，确定客观权重的方法主要包括最大熵技术法、主成分分析法、灰色关联法、相似系数法、离差最大化法、模糊聚类法、线性组合赋权法、敏感性分析法[1～14]等等。文献[15]针对熵权法下属性客观权重的分散度不高的问题, 提出了基于调节系数的改进的判断矩阵标准化处理方法。以不同决策者对相同方案同一属性的评价值为基础，根据数据稳定性与属性权重之间的正相关关系，提出以属性评价值的熵作为数据稳定性的度量，并由该熵值确定属性客观权重的方法。文献[16]从类空间类别分布模糊特性出发, 提出一种基于类空间模糊度的权重分配方法。文献[17]认为属性的评估值差异越小,其权重越小；差异越大,其权重也越大，提出了两种基于证据间差异性的客观权重确定方法。文献[18]针对交通环境风险评估过程中信息的不确定性、多样性及评估指标客观权重难以确定的问题，引入信息熵权法，基于对各种不确定信息熵的计算获得客观权重,进而建立基于熵权证据推理的评估模型。文献[19]引入一种基于粗糙集理论的权重确定方法，该方法不需要任何先验信息，即可完成权重计算，可使情报分析结果更加客观、有效。文献[20]针对指标权重未知的区间概率风险型混合多属性决策问题,提出一种基于熵权和投影理论的决策方法。文献[21]提出了表征不同指标间关联程度的灰关联深度系数，以其来确定指标客观权重大小的变动范围，运用极大熵准则构建规划模型来判断决策指标权重；但是该文提出的方法存在以下不足：一是灰关联深度系数经济含义模糊，不能有效反映评价指标的实际重要程度。根据文中灰关联深度系数的含义，某一指标权重的大小是由灰关联深度系数的取值范围所决定的。当某一指标原始值经规范化处理后取值越大，则会赋予该指标较小权重；反之，当某一指标原始值经规范化处理后取值越小，则会赋予该指标较大权重。二是灰关联深度系数易受评估对象数量的影响。随着评估对象数量的增加，灰关联深度系数呈减小趋势，不同指标之间关联的显著性大大降低；三是该文的评价指标客观权重极大熵配置模型存在较为严格的约束，可能导致无解的情况发生。

综观现有客观权重确定的方法和模型，我们可以看出这些方法和模型的基本思想主要是基于指标数据波动和数据独立程度进行赋权。利用评价指标值之间的差异性进行指标的客观赋权，仅仅反映了指标对评价对象的区分能力的大小，往往容易忽略指标权重本身相对重要程度的本质内涵，最直接的后果是可能会淘汰一些非常重要的指标，从而使评价结果有可能会严重失真。对评价指标权重的判断并不能仅仅依据指标值的区分能力，更为关键的是要考虑指标对被评价对象全体及所在系统的重要程度。

本文根据研究对象自然本质属性差异，将研究对象进行灰聚类分析，借鉴有无对比分析法的思想，定义了指标与全体被评价对象分类间的灰类敏感度系数，根据极大熵准则，建立了基于灰类敏感度系数的客观权重极大熵配置模型，从而找出对全体被评价对象类别影响最重要的指标，并赋予较大的权重。该方法基于事物本质属性差异的视角，探寻评价指标对被评价对象全体类别差异和类别变动的影响程度，为指标权重的判定提供了一种新方法。

1基于事物本质属性类型差异的灰色关联聚类模型

万物类象。在现实生活中，人们通常把在自然本质属性或某些属性上有相类似的事物归为一类。灰色关联聚类是根据由灰色关联度构成的灰色关联矩阵将一些评价指标或评价对象划分成若干个可定义类别的方法[22]。通过构建预设灰类的特征序列，利用灰色关联度，可以将评价对象划分到预设灰类中去。

1.1评价指标的无量纲化处理

考虑一个多指标决策问题，假设有n个评价对象(方案)，其组成的评价对象集为O={O1，O2，…，On},m个评价指标或属性组成的指标集为I={I1，I2,…,Im},m个评价指标的权重W={w1,w2,…,wm},第i个评价对象Oi在第j个评价指标Ij上的数值xi(j)(i=1,2,…，n;j=1,2,…,m),则O对I的评价矩阵为：

由于评价指标在量纲和数量级上存在着较大的差异，在计算过程中直接加权将无实际意义。在对评价指标体系进行综合聚类时，为消除各指标量纲不同和量级差异的影响，一般在完成数据收集工作后尚需对原始指标值进行无量纲化处理。其一般的处理步骤为：

Step 1判定评价指标体系中的每个指标属性值类型。指标属性值类型一般可分为效益型指标、成本型指标、适中型指标、偏离型指标、区间型指标、偏离区间型指标。其中，常用的指标属性值类型主要包括效益型指标、成本型指标、固定型指标，效益型指标是指标值越大越好的指标，成本型指标则相反，适中型指标是越接近某个适中值越好的指标。

Step 2依据指标属性值类型合理选择比较的标准值和处理方法。效益型指标、成本型指标、适中型指标的原始数据值可分别按照下述方法进行处理：

Step 3按照上述方法分别对评价矩阵中原始指标数值进行处理后，可以得到标准化的评价矩阵R：

1.2基于特征序列灰关联度的评估对象聚类过程

定义1设Xi={xi(j)|i=1,2,…,n;j=1,2,…,m}为系统行为序列，Xo=(xo(1),xo(2),…,xo(m))为参考序列。

称

在标准评价矩阵R中，各灰类的特征序列可以依据下述思想和步骤提取：

Step 2以minri(j)为端点，以(maxri(j)-minri(j))/(s-1)(s≥3)为步长，将灰类指标特征值向最大值方向进行逐步延拓，从而分别得到新的灰类特征序列，其特征值可用minri(j)+k(maxri(j)-minri(j))/(s-1)(s≥3,k=1,2,…,s-1)表示，直至延拓到maxri(j)为止(若以maxri(j)为端点，提取思路与之类似)。

2灰类敏感度系数的构建

事物的本质属性特征往往用评价指标数据予以表征和度量，评价指标在很大程度上决定着被评价事物的本质属性和类别等级。一方面，评价指标数据所蕴含的反映事物本质属性的信息量越大，对事物类别划分的区分程度也就越高；另一方面，评价指标对事物类别差异和变动的影响程度反映了不同评价指标对被评价事物全体的客观重要程度。例如，人们往往通过设计能够反映学生综合素质的评价体系对学生进行评价，一般可以将学生分为优、中、差三个类别。当学生按照综合素质属性进行分类时，同一类内的学生综合素质具有较高的相似度，不同类间学生综合素质具有较大的差异性，例如优类中学生的整体综合素质都比较高，差类中学生综合素质都比较低，优类学生的综合素质平均水平显著高于差类学生的综合素质平均水平，优类中任一学生综合素质水平都显著高于差类学生的综合素质平均水平；当反映学生综合素质的评价指标体系中的某个指标被去掉或者暂未被纳入考虑范围，所有被评价学生全体的分类也会发生变动，这种变动主要表现为两个方面：一是不同类别中学生数量的变动；另一个是被评价学生全体的类别调整。因此，可以借鉴有无对比分析的思想，通过对某个指标在整个评价指标体系中有无分析，判断和度量该指标对被评价对象全体类别变动的影响程度；我们可以将这种影响程度视为指标在整个评价体系中的相对重要程度，影响程度越大的指标应给予分配较大的权重。

设有n个评价对象(方案)，其组成的评价对象集为O={O1,O2,…,On}，利用对象所有评价指标数据，按照基于特征序列灰关联聚类方法共分成s个灰类。借鉴有无对比分析法的思想，为考量评价指标对评估对象全体类型划分的影响程度，将没有删除任何评价指标的对象分类作基准分类，将删除某个评价指标的对象分类视为比较分类，讨论删除任一评价指标后的评估对象分类的变动。如果因某个指标的删减，引发评价系统中灰类对象数量变化大，并且对象类型变动幅度大，那么我们就可以认为该指标对评价系统的影响程度大，该指标在整个评价指标体系中的相对重要程度就越大，评估对象的分类对这一指标也就越敏感，相应地该指标应赋予较大的权重。

定义2设基准分类的灰色关联矩阵为γ，删除第j个指标后的比较分类的灰色关联矩阵为γ′，γ和γ′分别表示如下：

3基于灰类敏感度系数的客观权重极大熵配置模型

E.T.Jaynes是信息论中的极大熵准则的创导者，他在该领域工作的时间从20世纪50年代跨到80年代，他的这一套思路和方法为社会所公认，一般称为极大熵准则。按照极大熵准则，人们应该挑选在一定约束条件下(常常是某些与随机变量有关的平均值)使得熵(或条件熵)能极大化的那种分布作为选定的分布[23]。借鉴文献[23]中的极大熵思想，客观权重极大熵配置模型构建与证明过程如下：

极大熵准则求解变量概率分布的数学规划问题模型：

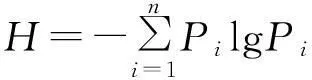
3.1目标函数的提出

按照极大熵准则的思想，由于各指标的真实权重是一个随机变量，具有不确定性，而“熵”的大小恰恰反映了评价指标的重要性的分布程度[24-25]。为了描述这种不确定性，可将权重wj理解为第j个指标Ij在评价指标集I中所占比重(“概率”)；并且认为在已知部分信息的基础上，权重熵值达到最大的并且满足约束条件所得到的权重值可能性最大。由此我们可以利用极大熵准则来对评价指标权重进行求解，建立目标规划方程，如式(1)所示：

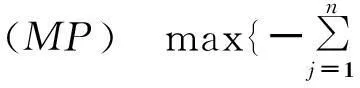
(1)

3.2约束条件的确定

首先，第一个约束条件。根据概率论的基础理论知识，可以很容易得到各评价指标的权重和为1，即为：

(2)

其次，第二个约束条件。根据基于特征序列灰关联度的评估对象聚类分析，可以将评估对象划分成s类(s为常数)，令分类结果按照序号依次从优到劣，那么我们可知优势类中任一评估对象的加权综合值均大于劣势类中任一评估对象的加权综合值。设yk(j)为第k类对象在第j个指标下的原始指标观测值，则有：

{wjyk(j)}>{wjyk+1(j)}(j=1,2,…,s-1)

(3)

再次，第三个约束条件。依据评估指标对对象类别差异的影响程度分析，我们可以根据评价系统类别对评估指标有无时的灰类敏感度系数，确定出各个评价指标对评价系统总体类型划分的影响程度，进而确定出各指标权重的相对排序。因此，我们可以得到以下的约束条件：

wi>wk,i≥1,k≤m,且i≠m

(4)

3.3模型的构建

根据式(1)和约束条件(2)～(4)，以建立如下多目标规划数学模型来求解指标权重，如式(5)所示：

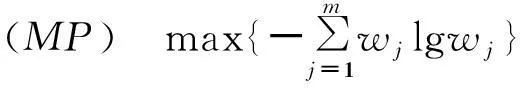
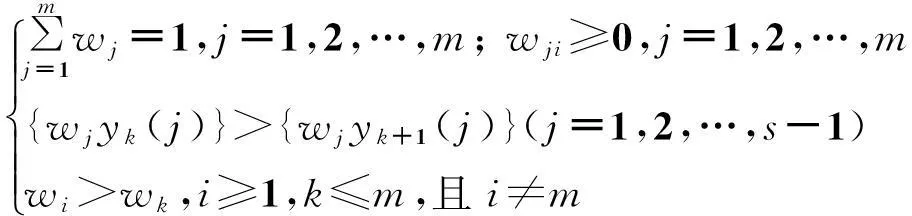
(5)

定理1指标客观权重的极大熵模型存在唯一最优解。

证明由极大熵模型：

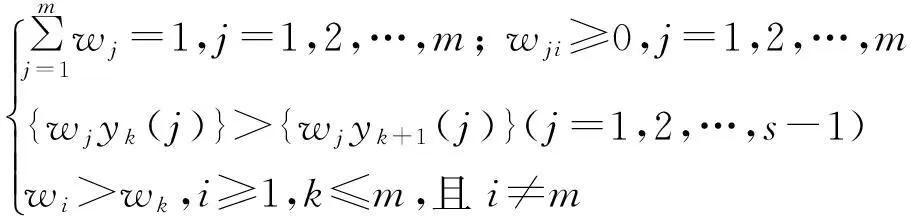
若极大熵模型为一个凸集上的凸规划问题，则必存在唯一的最优解。

将极大熵模型转化成如下模型：

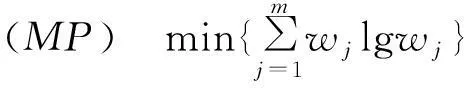
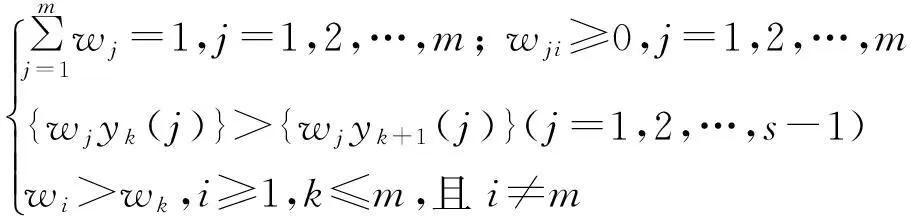
首先，判断目标函数为凸凹函数：(MP)为目标函数，则其海塞矩阵为：

因为00。

由海塞矩阵可知MP为凸函数，而约束条件为线性约束条件，所以为凸集。

因此，该极大熵模型为凸集上的凸规划问题，则必存在唯一的最优解。

3.4模型的求解

要求解评价指标权重，可以通过如下步骤进行：

第一步：构造拉格朗日函数；其中m为指标数，n为约束方程数，f为约束方程系数，α、β为待定参考系数。

(6)

由x=lnex可以将上式改写成：

第二步：借助不等式重要性质，对模型转化；

(7)

(8)

第三步：由式(8)求解参数。

(9)

(10)

第四步：将式(10)代入约束条件中，构造n个方程，即可求出n个β值，求出了β值后即可求出wj。

4案例研究

本文引用文献[26]中的案例，选取股票投资决策中股票的每股收益、每股净资产、每股公积金、净资产收益率、主营业务收入增长率、市盈率作为投资评级指标，并以2008年4月1日至6月30日钢铁行业6支具有代表性的股票为例，分别运用基于灰敏感度系数的极大熵模型法、熵权双基点法、灰深度关联系数法确定6个投资指标的权重，并对这6支股票的优劣进行排序，进而进行投资组合设计，比较这两种评价方法的优劣。各指标值如表1所示。

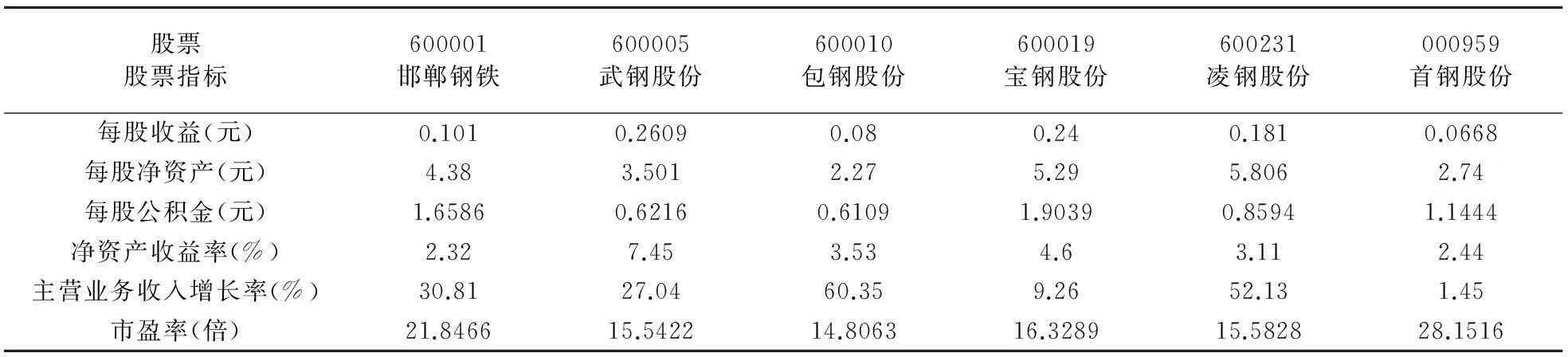
表1　6支股票指标值

Step 1在对评价指标进行无量纲化处理和提取预设的优良、中等、一般三个灰类特征序列的基础上，按照基于特征序列灰关联度的灰聚类方法对评估对象进行聚类分析，经过聚类我们可以得知：邯郸钢铁、武钢股份、宝钢股份归为一类，属于相对优良的类别；凌钢股份属于中等的类别；包钢股份、首钢股份归为一类，属于较为一般的类。根据优良类中股票投资价值要大于中等类，中等类中股票投资价值要大于一般类，我们可以得出式(11)：

(11)

Step 2通过有无对比分析，按照灰类敏感度系数的计算思路与步骤，逐一测算各评价指标对事物全体分类的影响程度。经过计算，我们可以得到各个指标的灰类敏感度系数：δ1=0.418,δ2=0.314,δ3=0.467,δ4=0.440,δ5=0.371,δ6=0.294。依据灰类敏感度系数的涵义，确定出各指标权重的相对排序，如式(12)所示：

w6≤w2≤w5≤w1≤w4≤w3

(12)

Step 3基于极大熵准则的客观权重配置模型建立与求解：利用式(5)中的指标客观权重的极大熵一般模型，以及式(11)、式(12)，构建基于极大熵准则的客观权重配置数学规划模型，如下式(13)所示：

(13)

得到投资决策评价指标的权重如表2所示。模型结果表明：每股公积金在6项指标之中对投资决策影响因素的权重最大，主营业务增长率和每股收益在投资决策影响因素中的权重较大，而每股净资产和净资产收益率的权重则偏低。这与在实际的股票投资中投资者十分注重对企业的获利能力基本相符。

表2评价指标权重

评价指标权重每股收益0.2357每股净资产0.0120每股公积金0.4940净资产收益率0.0120主营业务收入增长率0.2357市盈率0.0110

D(1)=2.050424,D(2)=2.658372,D(3)=2.0495167

D(4)=2.438744,D(5)=2.051771,D(6)=1.530662

文献[26]中假设投资者在2008年4月1日分别买入这六只股票持有至2008年6月30日，分别看它们的收益率：凌钢股份下跌9.08%，宝钢股份下跌23.12%，武钢股份下跌25.27%，首钢股份下跌30.87%，包钢股份下跌33.22%，邯郸钢铁下跌33.96%，据此对六只股票的实际行情排序如表3所示。并与文献[21,26]利用灰深度关联系数法、熵权双基点法计算的熵权以及优属度结果得出股票优劣程度的排序进行对比。

表3　股票投资价值的评价与多种方法的对比分析

根据表3所示，基于本文构建模型的评估结果显示，包钢股份和宝钢股份的评估结果与实际行情完成一致，均优于熵权双基点法和灰深度关联系数法；武钢股份、凌钢股份与宝钢股份的预测结果排列前三名，若投资者从6支股票中选择三支只股票进行风险投资，则基于本文权重设定方法的评估结果，选择这三支股票的投资组合更贴近实际行情，那么投资者就能保持最低的亏损率或最高的收益率。因此，基于灰类敏感度系数的极大熵模型求得的股票优劣程度对比文献[21]、[26]中的灰深度关联系数法、熵权双基点法更贴近股票实际行情，具有较强的可行性与实用性。

若投资者选择将100万元投资于这六支股票，按照本文以及熵权双基点法、灰深度关联系数法计算得到的评价值以及优属度的比例值进行投资，在经过3个月的投资期限后，投资者的收益分别为(注：由于受2008年股市整体下跌的影响，这6只股票的收益率均为负值)：

R熵权双基点法=(-33.96%)×0.09396+(-25.27%)×0.101663+(-33.22%)×0.134658+

(-23.12%)×0.340483+(-9.08%)×0.197532+(-30.87%)×0.131705=-0.23965

R灰深度关联系数=(-33.96%)×0.2914+(-25.27%)×0.2309+(-33.22%)×0.1194+

(-23.12%)×0.1194+(-9.08%)×0.1194+(-30.87%)×0.1194=-0.2722

R文本模型=(-33.96%)×0.2357+(-25.27%)×0.012+(-33.22%)×0.494+

(-23.12%)×0.012+(-9.08%)×0.2357+(-30.87%)×0.011=-0.27475

由上式可知，投资者按照本文的决策结果进行投资，与灰深度关联系数法相比将会会减少2471.87元的损失，与熵权双基点法相比将会减少35104.58元的损失。

5结语

本文从事物的本质属性出发，构建了基于特征序列的灰色关联聚类方法将事物划分到预设的类别中；在分类的基础上，采取有无对比分析的思想，定义了灰类敏感度系数的概念，反映不同评价指标对被评价对象全体类别变化的影响程度，用以表征和度量评价指标对被评价对象全体及所在系统的相对重要性；构建了基于灰类敏感度系数的评价指标客观权重极大熵配置模型，对影响事物分类结果的评价指标进行客观赋权；并以现实中的股票投资组合选择为案例，通过与其他方法的对比，该方法基本上能够正确客观配置事物的评价指标权重，在评价指标客观赋权与评价决策具有较大的优势，案例分析的结果可以为投资者提供较为可靠的建议，说明该方法具有较好的实用性和有效性。

参考文献：

[1]宣家骥.多目标决策[M].长沙:湖南科技出版社，1989

[2]李艳双,曾珍香,张闽,等.主成分分析法在多指标综合评价方法中的应用[J].河北工业大学学报,1999,28(1):94-97.

[3]Qing-Kui C, Kai-Zhan L I U, ZHANG B. Calculation method of objective index weight by entropy[J]. Journal of Hebei Institute of Architectural Science and Technology, 2000, 17(3): 40-42.

[4]周斌.由灰色关联度确定权重的客观多目标决策法[J].昆明理工大学学报(理工版),2003,5:159-161.

[5]熊文涛,齐欢,雍龙泉.一种新的基于离差最大化的客观权重确定模型[J].系统工程,2010,(5):95-98.

[6]Yanjun P, Kai-di L, Bo-wen Z. The method of determining the objective index weight in the synthetic evaluation system[J]. Systems Engineering-theory & Practice, 2001, 8: 37-42.

[7]Jian Liu. Using basic points to calculate the weighting coefficients in multiple objective decision making[J]. Systems Engineering-theory & Practice, 2001, 4: 6.

[8]陆文星,梁昌勇,丁勇.一种基于证据距离的客观权重确定方法[J].中国管理科学,2008,16(6):95-99.

[9]黄定轩,武振业,宗蕴璋.基于属性重要性的多属性客观权重分配方法[J].系统工程理论方法应用,2004,13(3):203-208.

[10]樊治平,张全,马建.多属性决策中权重确定的一种集成方法[J].管理科学学报,1998,1(3):50-53.

[11]庞彦军,刘开第,张博文.综合评价系统客观性指标权重的确定方法[J].系统工程理论与实践,2001,8(8):37-42.

[12]黄定轩,应可福,武振业.基于事例的多因素重要性排序确定方法及其应用[J].工业工程与管理,2003,8(3):24-27.

[13]李冬萍,明世祥,张文哲,等.基于敏感分析的评判指标权重确定方法及应用研究[J].全国金属矿山采矿新技术学术研讨与技术交流会论文集,2007.

[14]汪泽焱,顾红芳,益晓新,等.一种基于熵的线性组合赋权法[J].系统工程理论与实践,2003,23(3):112-116.

[15]周荣喜,范福云,何大义,等.多属性群决策中基于数据稳定性与主观偏好的综合熵权法[J].控制与决策,2012,27(8):1169-1174.

[16]张涛,洪文学.基于模糊度的计算几何分类器权重分配[J].控制与决策,2013,28(4):569-573.

[17]王海,冯向前,钱钢.语言环境下基于证据间差异性的属性权重确定方法[J].运筹与管理,2012,21(6):171-176.

[18]李伟,胡甚平.基于熵权证据推理的港口水域交通环境风险评估[J].上海海事大学学报,2012,33(3):10-10.

[19]周志远,沈固朝.粗糙集理论在情报分析指标权重确定中的应用[J].情报理论与实践,2012,35(009):61-65.

[20]刘培德,王娅姿.一种属性权重未知的区间概率风险型混合多属性决策方法[J].控制与决策,2012,27(2):276-280.

[21]汪群峰,金佳佳,米传民,等.基于灰关联深度系数的评价指标客观权重极大熵配置模型[J].控制与决策,2013,28(2):235-240.

[22]刘思峰,谢乃明.灰色系统理论及其应用[M].科学出版社,2008.

[23]邱菀华.管理决策与应用熵学[M].机械工业出版社,2002.

[24]何大义,邱菀华.运用熵极大化准则求解连续型不确定性决策问题[J].系统工程理论与实践,2002,16(09):86-92.

[25]刘善存,邱菀华,魏存平.极大熵方法求解双层多目标决策问题[J].系统工程理论与实践,2000,20(3):99-103.

[26]王兆红,詹伟,尤慧.熵权双基点法在股票投资价值评价中的应用[J].统计与决策,2009,(3):45-47.