基于神经网络与遗传算法的锅炉系统的优化

鞠云鹏，常德功

（青岛科技大学 机电工程学院，青岛 266061）

循环流化床锅炉[1-2]是应用清洁煤燃烧技术的成果，它是利用脱硫剂（石灰石）使煤在流化床上燃烧时脱硫。锅炉燃烧过程是一个复杂的物理、化学过程，牵涉到的输入和输出变量达160多个[3-4]。依靠专业技术人员的经验和传统热力学的计算分析方法，仅能解决单个输入变量和输出目标值的问题。随着计算机技术和应用数学方法进入工业领域，使得解决多变量之间关系的难题变得容易了许多。但是，锅炉运行的多目标参数间存在着诸多矛盾，譬如，燃烧效率与氮氧化物的排放之间的矛盾、低氧燃烧与还原性气体的腐蚀之间的矛盾等等。这些问题就需要用系统的观念去全面考虑和协调多目标之间的关系。借助先进的数学和计算机手段，利用人工智能神经网络[5-7]可以解决多变量非线性关系的问题。在对系统深刻理解的基础上，可以把各种数据信息与锅炉的经济、安全和可靠等性能指标之间的关系量化，利用统计学非线性回归和人工智能神经网络技术将锅炉的运行参数与性能指标之间的关系用数学模型的方式表达出来[6-7]。

遗传算法[8-11]是一种随机搜索算法，并且是一种模仿生物进化过程的进化算法。这种算法具有较强的适应性，除了需要知道适应度函数之外，几乎不需要其他的先验知识。另外，它不受搜索空间的限制性假设的约束，不要求连续性，能以很大的概率从高维问题中找到最优解，并且能够搜索到满足不同需求条件下的最佳运行参数组合（借助优化运算）。本文首先通过锅炉厂参数的历史数据建立BP神经网络并进行训练，然后通过遗传算法建立各参数的优化组合，通过训练好的网络预测出优化效率，并将优化效率对应的风煤比数据作为反馈信号引入锅炉性能优化系统中，以达到提高锅炉效率的目的。

1 预测优化原理

1.1 预测模型的建立

本设计建立三层BP神经网络，为方便模型的建立，引入以下符号：

Xk=，（k=1，2，3，…，n）为输入向量形式，其中：n为输入层神经元个数。Yk=为期望输出向量形式，其中，q为输出层神经元个数。为隐含层输入向量，为隐含层输出向量，其中，p为隐含层神经元个数。Lk=为输出层输入向量，Ck=为输出层实际输出向量。 w=｛wij｝，（i=1，2，3，…，n， j=1，2，3，…，p）为隐含层与输入层间的权值。 V=｛vij｝，（t=1，2，3，…，q， j=1，2，3，…，p）为输出层与隐含层间的权值。 θ=｛θj｝，（ j=1，2，3，…，p）为隐含层神经元阈值，γ＝｛γt｝，（t=1，2，3，…，q）为输出层神经元阈值。

首先将［-1 1］之间的随机数赋给权值v，w以及阈值 γ，θ，将一组（Xk，Yk）提供给网络，作为学习模式对，k=1，2，3，…，m（m 为学习组数）。

根据式（1）和式（2）计算隐含层神经元的输出值和输入值为

根据式（3）和式（4）计算输出层神经元的输出值和输入值为

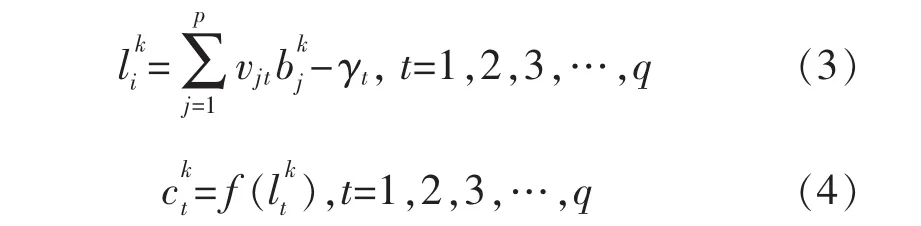
根据式（5）和式（6）分别计算出输出层和隐含层神经元的校正误差和为

以 α 为学习速率，0＜α＜1，根据式（7）和式（8）来修正输出层至隐含层间的连接权值v以及输出层神经元的阈值γ为

以 β 为学习速率，0＜ β＜1，根据式（9）和式（10）来修正隐含层至输入层间的连接权值w以及隐含层神经元的阈值θ为

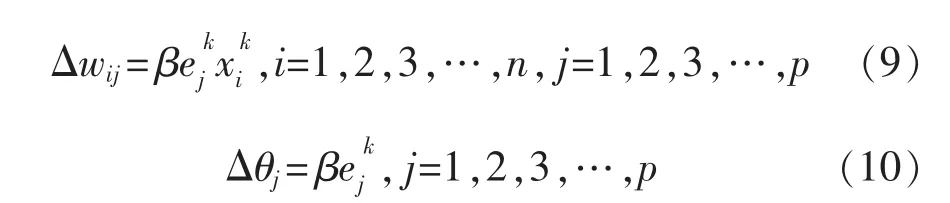
随机选取下一组训练数据，并提供给上述算法，直至将所有训练数据训练完毕。判断全局误差E是否满足所要求精度，即E≤ε。如果满足，则停止计算，否则更新训练组数，继续计算。计算完毕后，新的网络模型可用于锅炉效率值的预测。

1.2 优化算法流程

本文通过遗传算法来搜索锅炉效率期望值所对应的风煤比值关系，并将优化后的风煤比作为反馈信号引入锅炉系统中，以提高锅炉效率。优化算法流程如下：

1）锅炉参数编码

将个体用 （ai1，ai2，ai3，ai4，ai5，ai6，ai7，ai8，ai9，ai10，ai11）来编码，个体中的基因分别代表锅炉效率、入炉煤量、二次风流量、上一次风流量、下一次风流量、主蒸汽流量、氧量计、主蒸汽压力、炉膛密上温度、给水温度、主蒸汽温度。根据表1可得到各参数的取值范围，将个体基因 ai1，ai2，…，ai11分别赋予取值范围内的随机数值。

2）适应度函数

本研究中的适应度函数采用BP神经网络预测模型，输出层处理单元的输入加权和如式（3）所示，输出层神经元的转移函数采用Sigmoid函数，数学表达式为

3）选择操作

采用轮盘赌选择算法和适应度函数来进行选择操作，将适应度值高的个体进行复制得到下一代。

4）交叉操作

在所复制的个体中采用随机方法进行交叉操作，交叉操作函数如下：

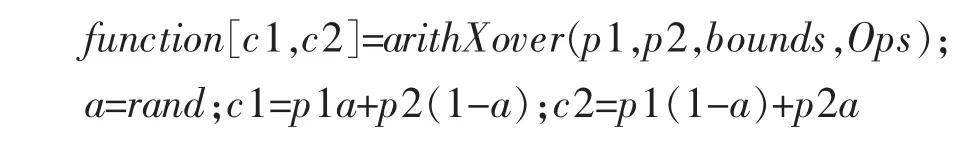
其中：p1，p2 为父代个体；c1，c2 为子代个体；bounds为取值范围；Ops为可选项。

5）变异操作

变异操作中变异点的选取采用随机与近似的方法，变异操作函数如下：

其中：parent为父代个体；bounds为取值范围；Ops为可选项。

遗传算法优化的具体运算流程如图1所示。

2 锅炉效率的优化

2.1 优化方案的选取

锅炉系统的候选优化方案有3种。

图1 遗传算法优化流程Fig.1 Genetic algorithm optimization flowchart

1）简化方案：不安装任何测点、运行优化软件的服务器系统和工作站、现场做锅炉运行优化试验并提供优化运行指导曲线。

2）在线开环指导优化方案：优化方案是基于Matlab 6.5工具箱函数自行开发的一套优化程序。首先，运用Matlab VC++2005编译器将函数打包成com组件，即dll文件，然后，运用C#（可视化开发工具）调用程序并开发界面。

3）在线闭环控制优化方案（根据中国的煤质、设备等状况暂不推荐使用此方案）。

本论文所采用的是在线开环指导锅炉运行优化方案。锅炉运行优化系统在线开环指导优化运行，需要与DCS系统接口进行数据交换和发布优化运行提示和控制指令。锅炉运行优化系统与电厂现有的DCS数据库交换数据，只需要根据具体DCS系统的通讯方式和I/O接口规定，以DCS-数据库系统－锅炉运行优化系统方式建立通信。开环系统只需从DCS系统采集数据，优化结果不进入DCS系统。

2.2 BP神经网络的训练

本研究中所采用的网络结构为3层，根据kol mogorov定理[12]可确定隐含层神经元的个数n，n=2m+1，其中，m为输入量个数。锅炉优化系统从锅炉厂现有的DCS数据库中提取150组所需运行参数，主要运行参数如表1所示。基于表1锅炉系统运行数据（前75组），通过BP神经网络可建立锅炉参数与效率间的函数模型。

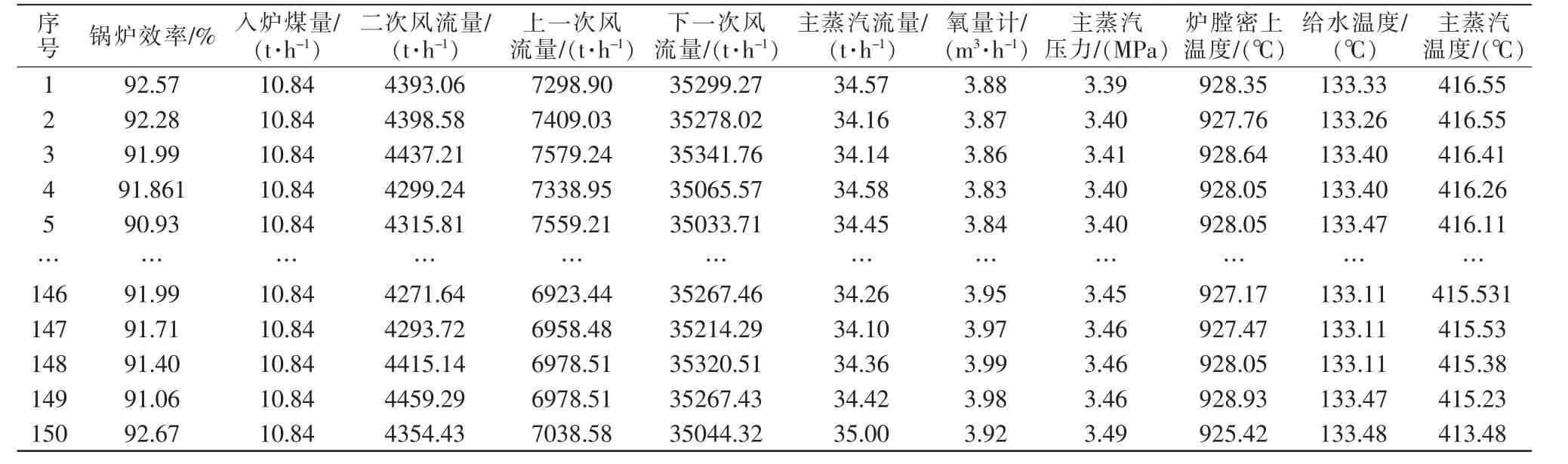
表1 锅炉系统主要运行参数Tab.1 Boiler system operating parameter

2.3 锅炉参数的优化

将锅炉输入参数（入炉煤量、二次风流量、上一次风流量、下一次风流量、主蒸汽流量、氧量计、主蒸汽压力、炉膛密上温度、给水温度、主蒸汽温度）以及输出参数（锅炉效率）进行浮点数编码，并根据表1数据确定各参数的范围，进行种群的初始化。初始化的种群经过选择、交叉、变异以及适应度函数的计算，最终得到期望效率值。将期望效率值所对应的风煤比引入锅炉系统即可达到优化锅炉效率的目的。根据开环指导优化方案，在取数时间长度为10 min，优化频率为650 s，锅炉效率设定值为98%的情况下所得到的锅炉优化参数如表2所示。

表2 锅炉优化参数Tab.2 Boiler optimization parameters

3 结果与分析

基于表1锅炉系统运行数据（前75组），通过BP神经网络建立锅炉参数与效率间的函数模型。并以表1中后75组数据作为校验数据，以验证网络预测的精度。为更好地了解BP神经网络的预测精度，针对窑炉运行数据建立了4个网络预测模型。同时，为更好地了解遗传算法与神经网络相结合的优越性，针对窑炉运行数据建立了6组差值（锅炉效率优化前后的差值）。图2是网络预测值与校验数据的比较。图3是采用遗传算法优化后的锅炉效率输出值与初始数据（未经优化前的数据）的差值。

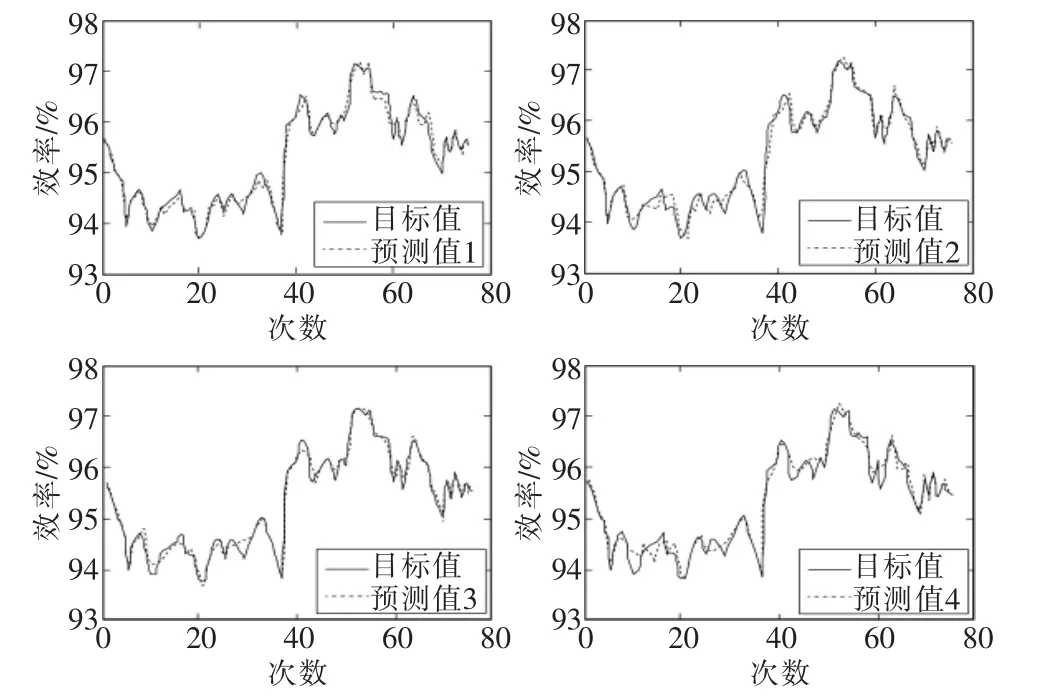
图2 锅炉效率的实际数据与神经网络预测模型输出的比较Fig.2 Comparison of actual data with the output of the neural network prediction model

图3 锅炉效率优化值与初始值的差值Fig.3 Difference between optimal values and the initial values

由图2可知，4组曲线是BP神经网络预测值与校验数据的比较，与此同时，所用预测模型是从多个所建模型中随机抽取的，因此预测值能较好地体现网络的预测能力。4个BP神经网络预测模型中，锅炉实际效率曲线与神经网络建模后的输出效率曲线的差值较小，二者曲线近乎重合，这说明：BP神经网络所预测的效率值与原始效率的拟合程度较高，BP神经网络具有较高的预测精度，可用于锅炉系统效率预测优化中。

由图3可知，6组曲线是采用遗传算法优化后的锅炉效率输出值与初始数据 （未经优化前的数据）的差值，采用优化方法以后计算出的锅炉效率与原始效率差值几乎全部大于零，最大差值已接近3.5%，根据现场采集数据和综合分析，锅炉性能优化系统投入使用后，预期可以达到降低供电煤耗2 g/（kWh）左右；降低氮氧化物排放量 150 mg/m3。根据目前已经取得的优化业绩，锅炉年节约煤耗（按2 g/（kWh）计算）：（2×10-6） t/（kWh）×300 MW×6000 h×700元/t=252万元；按目前平均煤价700元/t计算，通过锅炉性能优化节煤年直接经济效益至少在252万元人民币以上。参照1004 t蒸发量锅炉参数测算：总排烟量1.3×106m3/h；按照年运行6000 h，以降低100 mg/m3估算（实际优化值需根据现场情况确定）。按照2004年7月1日执行的《排污费征收标准管理办法》，NOx排放按实际排放污染当量收费，每污染当量NOx收费0.6元（每污染当量为0.95 kg）。则年NOx排放节约费用为

1.3×106m3/h×100×10-6kg/m3×6000 h×0.6 元/0.95 kg＝49.26 万元

年总节约费用为

252万元＋49.26万元＝301.26万元以上。

4 结语

锅炉优化系统从锅炉厂现有的DCS数据库中提取所需的运行参数。通过人工智能神经网络建立各参数之间的模型，利用遗传算法得到各参数的优化组合，为锅炉系统的优化提供保障。通过优化验证曲线可以看出，采用BP神经网络能够相对准确的预测出锅炉效率，同时遗传算法能够较好地优化参数，使锅炉效率提高0.5%～3%。此优化算法也可推广应用到玻璃窑炉厂配料系统中。与此同时，本文的优化也存在不完善的地方，比如，优化方案所选择的是在线开环指导方式，这主要是由中国的煤质、设备等状况所决定的。进一步完善优化方法，提高锅炉效率是下一步需要做的工作。

[1]Zhang Nan，Lu Bona，Wang Wei，et al.3D CFD simulation of hydrodynamics of a 150 MWe circulating fluidized bed boiler[J].Chemical Engineering Journal，2010，162（2）：821-828.

[2]张瑞卿，杨海瑞，吕俊复.应用于循环流化床锅炉气固流动和燃烧的 CPFD 数值模拟[J].中国电机工程学报，2013，33（23）：75-83.

[3]苏建民.燃烧劣质无烟煤300 MW循环流化床锅炉节能减排特性的研究[J].动力工程学报，2010，30（9）：663-667.

[4]张恺，曹长青，赵亚南.气液固循环流化床预分布器附近流体动力学的数值研究[J].青岛科技大学学报：自然科学版，2010，31（1）：51-54.

[5]赵彤，曹世伟，赵品.基于神经网络MIMO非仿射系统自适应控制[J].青岛科技大学学报：自然科学版，2010，31（3）：317-320.

[6]刘瑞叶，黄磊.基于动态神经网络的风电场输出功率预测[J].电力系统自动化，2012，36（11）：19-22.

[7]Wang C，Wang M，Liu T F，et al.Learning from ISS-modular adaptive NN control of nonlinear strict-feedback systems[J].IEEE Transactions on Neural Networks and Learning Systems，2012，23（10）：1539-1550.

[8]刘军，张利建，薛明.基于遗传算法的仿人智能控制[J].青岛科技大学学报：自然科学版，2007，28（2）：162-165.

[9]王东风，任燕燕，刘长良.基于量子遗传算法的循环流化床锅炉模型辨识[J].动力工程学报，2013，33（10）：782-788.

[10]金弟，刘杰，杨博.局部搜索与遗传算法结合的大规模复杂网络社区探测[J].自动化学报，2011，37（7）：873-882.

[11]梁亚澜，聂长海.覆盖表生成的遗传算法配置参数优化[J].计算机学报，2012，35（7）：1522-1538.

[12]于彬.基于小波分析的BP神经网络膜蛋白跨膜螺旋区段预测[J].青岛科技大学学报：自然科学版，2010，31（6）：583-586.