结合小波去噪的PCA工业过程传感器故障检测

（武汉大学 动力与机械学院，武汉 430072）

主元分析PCA是一种多变量分析技术，在数据压缩、模式识别、信号处理和过程监控等领域均获得广泛运用[1-3]。PCA将原始的高维度数据投影到低维空间，以消除各个变量之间的弱相关性，降低数据的复杂度；从而能够更容易地从海量历史数据中提取有用信息[4]。PCA将数据空间分解为2个正交子空间：主元空间PCS（principal component sub space）和残差空间 RS（residual subspace），利用主元模型求取SPE、T2统计量[5]。由于工业现场存在噪声且噪声不满足高斯分布，使得PCA在工业现场传感器故障检测中存在一定程度的故障误检测问题。为此，如何削弱工业现场噪声的影响，降低故障误检测率值得进行研究。

小波分析是信号处理的有力工具，可保证在信号品质不受影响的前提下滤去信号中的噪声[6-8]。1984 年，文献[9]提出了“小波”（wavelet）的概念，提出用一个函数的时移性和尺度组合表示信号的新思想。1989年，文献[10]提出信号的多分辨率分析与快速重构算法，随后小波变换快速走向实用化。小波去噪在工业过程也获得了广泛运用，文献[11]通过滑动窗将小波分析与PCA结合，用于TE化工过程故障检测，论证了该方法的可行性。

本文结合小波去噪和PCA，通过滑动窗对PCA的SPE、T2统计量进行小波去噪，削弱噪声对SPE、T2统计量的影响。文中提出的方法在电厂水处理过程中进行了仿真，结果表明该方法可有效减少故障误检测。

1 PCA故障误检测

设工业生产过程有m个传感器，PCA故障检测包含以下3个步骤：

步骤1数据收集和标准化。构造测量数据矩阵 X1=［x1，x2，…，xn］T∈Rn×m，其中 X1的每一列表示一个变量，每一行表示一个样本。对X1的每一个样本 xi（i∈［1，n］）进行标准化处理，得到新样本集 X。

步骤2特征值分解及SPE和Hotelling T2控制限求取。X按照式（1）分解：

步骤3在线计算SPE和Hotelling T2统计量并检测故障。对实测样本x∈R1×m（已经标准化处理），计算其SPE和Hotelling T2统计量。按照故障检测逻辑诊断当前系统运行状态：当SPE＞SPElim或时，则判定故障产生，否则判定无故障。有关PCA故障检测可参考文献[12-14]。

PCA故障检测在工业现场运用时，SPE、T2统计量波动剧烈，容易超过控制限导致故障误检测。为了降低故障误检测率，本文利用小波方法滤除SPE、T2统计量的噪声。

2 小波PCA故障检测

2.1 小波变换与去噪

连续小波变换CWT（continuous wavelet transform）的数学表达式为

式中：a，τ分别为尺度因子和平移因子；ψ（t）为母函数；ψ*（t）为其共轭函数。尺度因子a控制函数的伸缩：当a增大时，函数时窗变宽；当a减小时，函数时窗变窄。这样小波变换就可以对信号进行多尺度细化，同时得到良好的时间、频率分辨率。

式（2）中尺度因子a连续变换，导致计算量大，实际工程应用中，常用离散小波变换DWT（discrete wavelet transform）。能在保证信号不失真的同时，减小计算量。文献[10]中提出了正交小波快速算法，得到了广泛运用。本文也采用这种算法进行小波分解，得到各尺度的小波系数和近似系数，然后通过离散小波逆变换IDWT（inverse discrete wavelet transform）重构信号。

以信号f（t）的小波三层分解为例，小波分解如图1所示。

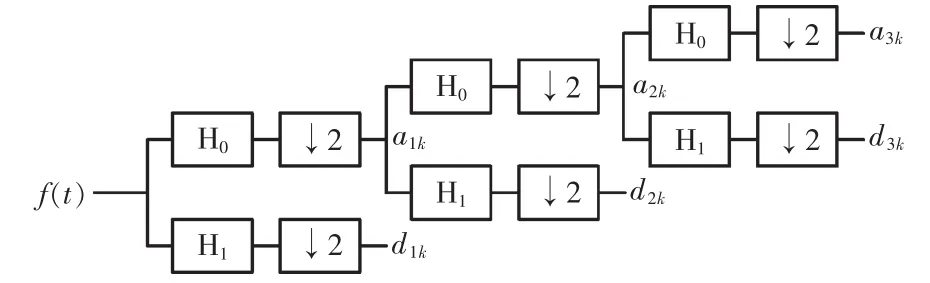
图1 信号的小波三层分解Fig.1 Three level decomposition of signal

图1中：H0，H1分别为低通、高通滤波器；↓2代表下采样过程。信号f（t）三层分解后得：

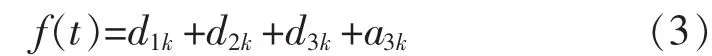
文献[6-8]提出了非线性小波变换阈值去噪法，得到了广泛运用。小波变换可将信号的“能量”集中于少数小波系数；而白噪声由于其无序性，其“能量”分散于各小波系数。随着分解的进行，白噪声的小波系数变小，信号的小波系数远大于白噪声的小波系数。因此，可找到合适的阈值δ，将小于δ的小波系数滤去，得到纯净的小波系数。最后将去噪后的小波系数进行重构即可获得滤波后的信号。

Matlab小波工具箱提供了小波去噪函数，本文即采用Matlab工具箱实现信号去噪[15]。

2.2 结合小波去噪的PCA故障检测

2.2.1 小波PCA故障检测流程

传统PCA故障检测方法在实际工程应用中SPE和T2统计量波动剧烈，易导致故障误检测。本文采用小波去噪滤除SPE和T2统计量的噪声，以减少PCA故障误检测率。结合小波去噪的PCA故障检测流程如下：

①PCA离线建模。利用历史正常工况下的数据得到负载矩阵Pa、得分矩阵T、主元个数a，以及SPElim和控制限。

②PCA统计量在线计算。对于实测数据样本x∈R1×m，计算其对应的 SPE 和 T2统计量。

③小波去噪。通过滑动窗对SPE和T2统计量进行小波去噪。构建长度为wlen的SPE和T2统计量滑动窗，根据小波函数、分解层数lev、阈值、阈值处理方式和阈值重调规则进行小波去噪，获得去噪后的统计量。

2.2.2 小波去噪参数的选取

以上步骤中，小波去噪是关键环节，对故障误检测率影响大。故需要研究小波去噪的参数选取问题。

①小波函数选取：在小波分析中陆续出现了一系列经典小波系，例如Haar小波、Daubechies小波系、Symlets小波系、Coiflets小波系和Spline小波系等[9]。其中，正交小波系可根据快速算法得到信号完全重构，计算量较小。故本文采用正交小波系作为基小波。正交小波系有 Haar小波、Daubechies、Symlets和Coiflets小波系。

Haar小波是Daubechies小波系中第一个小波函数。Daubechies小波系和Symlets小波系分别有45种小波。小波序号越大，小波函数计算量越大，本文选取了Daubechies小波系和Symlets小波系的前15 个小波，即 db1，…，db15 和 sym1，…，sym15。

Coiflet小波系包含5种小波函数，它们所需的计算量不大。在后续敏感性分析中选取Coiflet小波系全部5个小波函数，即coif1，…，coif5进行对比分析。

②阈值处理方式。小波去噪有2种通用的阈值处理方式：软阈值法和硬阈值法。设WT为小波系数，δ为阈值，软、硬阈值法可表示为

i）硬阈值法（hard）

ii）软阈值法（soft）

硬阈值法处理方式简单，但会造成处理后小波系数的不连续，引起重构信号振荡；而软阈值法处理后小波系数的连续性好，在工业上运用更广泛。

③阈值选取规则。Matlab工具箱中，有4种阈值选取规则[15]：固定式阈值（sqtwolog）、Stein 无偏估计阈值（rigrsure）、启发式阈值（heursure）和极大极小值阈值（minimax）。不同的阈值对去噪效果造成影响。

④阈值重调方法：Matlab小波工具箱里，有3种阈值重调方法：one、sln、mln。它们规定了各层小波系数采用的阈值是否重调的规则。

⑤分解层数。分解层数lev受滑动窗长度wlen影响。例如wlen=8，由于下采样过程使小波系数样本数减半，则lev最大为3。滑动窗长度wlen限制了分解层数lev的大小。

⑥滑动窗参数。滑动窗参数包括滑动窗长度wlen和滑动窗步长wstep。本文选取滑动窗长度wlen为2的正整数倍，以避免边界失真，保证信号重建的准确性[16]。滑动窗步长wstep应小于或等于wlen，还需考虑计算量因素。

3 应用研究

3.1 热力发电厂水处理流程

本文以1000 MW热力发电厂补给水处理流程为对象验证本文提出的方法。水处理工艺如图2所示。原水分别经预处理——阳床/阴床——混床，最终出水。阳床、阴床、混床中的混合离子树脂置换水中的盐，达到净化水质的目的。水处理流程配备了大量的传感器，对水质指标进行实时监测[17]。本文从水处理流程选取了12个主要传感器作为故障检测对象，如表1所示。

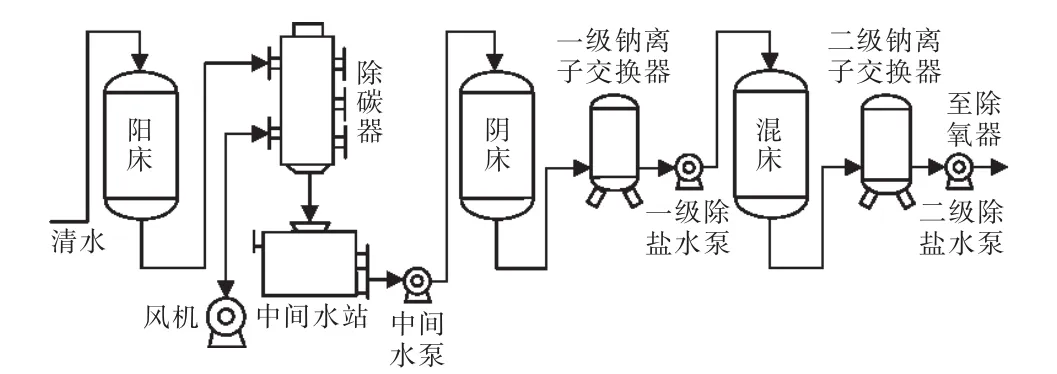
图2 阳-阴-混床水处理流程Fig.2 Flow chart of cation-anion-mixed bed

表1 传感器列表Tab.1 List of sensors

3.2 小波PCA故障误检测方法验证

首先从电厂SIS系统中选取正常、稳定的运行数据为学习样本，采样时间为5 s，样本容量100。以该段数据为训练样本建模主元模型。再选择同一工况下另一组稳态数据为检测样本集，采样时间5 s，样本容量1000。分别采用传统PCA和结合小波去噪的PCA进行水处理过程故障检测，2种方法的验证结果分别如图3和图4所示。

图4中小波去噪参数设置如下：db10小波函数、软阈值、固定式阈值、mln阈值重调、wlen=64、wstep=6、lev=3）。

图3 传统PCA SPE、T2控制Fig.3 SPE，T2statistics of classical PCA method

图4 结合小波去噪PCA SPE、T2控制Fig.4 SPE，T2statistics of PCA combined with wavelet denoising

为了便于书写，本文将小波去噪参数写为以下形式：（db10，soft，sqtwolog，mln，wlen=64，wstep=6，lev=3）。

图3表明传统PCA方法检测样本SPE、T2控制量存在“毛刺”，且SPE、T2的峰值超出了对应的控制限，导致故障误报。虽然故障误判的持续时间短，仅为1～5个采样时刻，但这些短时间的故障误判影响了PCA故障检测方法的实际使用效果。图4表明用小波去噪后，PCA SPE、T2控制量在保留信号趋势的同时，滤除了毛刺，有效解决了故障误报的问题。

传统PCA方法与结合小波去噪PCA方法的故障误报性能如表2所示。

表2 传统PCA与结合小波去噪PCA性能统计Tab.2 Comparison between classical PCA and PCA combined with wavelet denoising

表2表明，通过对PCA SPE、T2统计量进行小波去噪，能有效消除故障误报，使PCA方法在工业生产过程的运用更加实用。图4为一种去噪参数组合下的特例分析，为了更加彻底地理解小波参数的影响，以下将对小波去噪参数的敏感性进行分析，以指导PCA小波去噪参数的选取。

3.3 小波去噪参数的敏感性研究

小波去噪是影响PCA故障误报的关键环节。小波去噪参数多，对去噪性能都有影响，故需要对小波去噪参数的敏感性进行分析。本文小波去噪最终服务于降低故障误报率，故将系统的故障误报次数作为小波去噪效果的评判标准。若某一小波参数降低了故障误报次数，判断该参数组合优化；反之，则判定参数组合劣化。

3.3.1 小波系

首先对小波系进行分析，在其他参数固定时分别选用 Symlets、Daubechies和Coiflets小波系的小波函数进行对比研究。各小波系小波函数滤波效果如图 5 所示， 其他参数设置为（soft，sqtwolog，mln，wlen=64，lev=3，）。图5中将误报次数作为优劣评判指标。

图5 各小波系滤波效果对比Fig.5 Comparison among wavelet species

图5表明，随着小波函数序号的增大，各小波系都能减少误报次数。其中sym2、sym10和db2对系统性能的提升作用较差，Symlets小波系滤波效果不稳定，Coiflet小波系对性能敏感性较低。Daubechies小波系中小波函数序号大于8的小波都能消除误报，比Symlets和Coiflet小波系稳定；且Daubechies小波系比Symlets小波系计算量小。故Daubechies小波系，特别是小波函数序号大于8的小波函数具有优势。以下参数分析就将重点针对Daubechies小波系开展。

3.3.2 阈值处理方式

当其他参数设置为（Daubechies小波系，sqtwolog，mln，wlen=64，wstep=4，lev=4），软、硬阈值滤波效果对比如图6所示。

图6 软硬阈值滤波效果对比Fig.6 Comparison between soft and hard threshold

图6表明，对Daubechies小波系的各个小波，软阈值对性能的提升都远好于硬阈值，且软阈值滤波效果更加稳定。

3.3.3 阈值选取规则

取其他小波参数为（Daubechies小波系，soft，mln，wlen=64，wstep=4，lev=4），阈值选取规则滤波效果对比如图7所示。

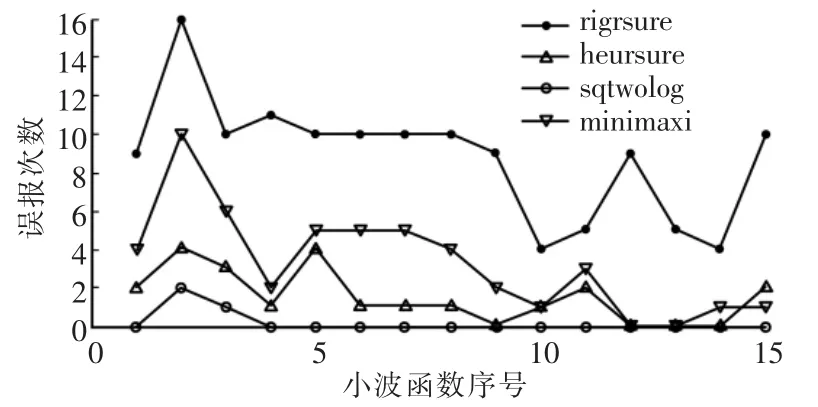
图7 各阈值滤波效果对比Fig.7 Comparison among threshold selection rule

图7表明，对Daubechies小波系的各个小波，sqtwolog阈值滤波效果良好、稳定，具有较大优势。

3.3.4 阈值重调

取其他小波参数为（Daubechies小波系，soft，sqtwolog，wlen=64，wstep=4，lev=4），阈值重调滤波效果对比如图8所示。

图8 阈值重调滤波效果对比Fig.8 Comparison among threshold rescaling method

图8表明，对Daubechies小波系的各个小波，mln参数滤波效果最好。这是由于水处理过程现场存在非高斯白噪声，在每一层都需要进行阈值重调。

3.3.5 分解层数

当其他小波参数选取为（Daubechies小波系，soft，sqtwolog，wlen=64，wstep=4，lev=4），分解层数滤波效果对比如图9所示。

图9 分解层数滤波效果对比Fig.9 Comparison among decomposition level

图9表明，随着lev的上升，系统故障误报数明显下降，滤波效果显著提升。当lev=4时，已满足系统正常运行要求，继续增加lev对性能的提升不敏感，且增加了计算量。综合考虑计算量与滤波效果，建议lev为4或者5。

3.3.6 滑动窗

滑动窗长度wlen与滑动窗步长wstep对滤波效果无明显的影响。分解层数lev受wlen的限制，当lev=4时，系统故障误报率满足系统要求，综合考虑建议wlen为64或者128，滑动窗步长wstep为4～10。

4 结语

传统PCA在工业现场故障诊断中易出现故障误检测问题，本文将小波去噪应用于PCA，旨在提升故障检测的性能。以某1000 MW热力发电厂补给水处理流程为对象，以该流程典型工况下运行数据为基础验证了小波PCA故障检测算法，结果表明结合小波去噪的PCA方法能有效减少系统误报次数。

本文还对小波去噪参数进行了敏感性分析，对小波滤波参数的设置提出了建议。建议使用Daubechies小波系小波序号大于8的小波函数，采用软阈值、sqtwolog、mln、4或 5层分解，滑动窗长度为64或128，滑动窗步长为4～10。本文提出了利用小波去噪降低故障误报率的方法和步骤，提升了PCA故障检测的性能，使其更加实用化。

[1]张大海，刘宇穗，张世荣，等.发电厂水处理流程传感器故障检测系统研究[J].自动化与仪表，2014，29（5）：9-13.

[2]Chen G，Qian S E.Denoising of hyperspectral imagery using principal component analys is and waveletshrinkage[J].Geoscience and Remote Sensing，IEEE Transactionson，2011，49（3）：973-980.

[3]王健，冯健，韩志艳.基于流形学习的局部保持PCA算法在故障检测中的应用[J].控制与决策，2013（5）：683-687.

[4]周东华，李钢，李元.数据驱动的工业过程故障诊断技术：基于主元分析与偏最小二乘的方法[M].北京：科学出版社，2011.

[5]Shams B，Budman H M，Duever T A.Fault detection，identification and diagnosis using CUSUM based PCA[J].Chemical Engineering Science，2011，66（20）：4488-4498.

[6]Donoho D L.Adapting to unknown smoothnessvia wavelet shrinkage[J].J Amer Statist Assoc，1995，90：1200-1224.

[7]Donoho D L，Johnstone I.Wavelet shrinkage asymptopia[J].Journal of Royal Statistical Society，1995，57（2）：301-369.

[8]Donoho D L.Denoising by soft-thresholding[J].IEEE Transaction on Information，1995（3）：613-627.

[9]Grossmann A，Morlet J.Decomposition of hardy functions into square integrable wavelets of constant shape[J].SIAM journal on mathematical analysis，1984，15（4）：723-736.

[10]Mallat S，Hwang W L.Singularity detection and processing with wavelets[J].Information Theory，IEEE Transactions on，1992，38（2）：617-643.

[11]Li S，Wen J.A model-based fault detection and diagnostic methodology based on PCA method and wavelet transform[J].Energy and Buildings，2014，68：63-71.

[12]牛征，刘吉臻，牛玉广.动态多主元模型故障检测方法在变工况过程中的应用[J].动力工程，2005，25（3）：426-426.

[13]Ding S，Zhang P，Ding E，et al.On the application of PCA technique to fault diagnosis[J].Tsinghua Science& Technology，2010，15（2）：138-144.

[14]Jeng J C.Adaptive process monitoring using efficient recursive PCA and moving window PCA algorithms[J].Journal of the Taiwan Institute of Chemical Engineers，2010，41（4）：475-481.

[15]Michel M，Yves M，Georges O，et al.Wavelet toolbox for use with MATLAB[J].Wavelet Toolbox User’s Guilde，1997.

[16]Strang G，Nguyen T.Wavelets and Filter Banks[M].SIAM，1996.

[17]Faust S D，Aly O M.Adsorption Processes for Water Treatment[M].Elsevier，2013.