网络交叉口群关联性研究
网络交叉口群关联性研究
汪圣伟,韩印
(上海理工大学 管理学院, 上海 200093)
[摘要]通过分析交叉口间距、路段流量、周期比对相邻交叉口关联性的影响,提出量化相邻交叉口关联性的交通度量指标,通过仿真验证了度量指标的合理性,在此基础上进一步提出了网络交叉口群中交叉口之间关联性的计算方法以及相应的网络交叉口群子区域划分的原则。运用该原则进行案例说明,结果证明了其有效性,为以后进行网络交叉口群的交叉口子区域划分的研究提供了一种新的方法。
[关键词]城市交通;交叉口群子区域划分;网络交叉口群关联性;交叉口群;相邻交叉口关联性
[文章编号]1673-2944(2015)04-0030-06
[中图分类号]TU984.191
收稿日期:2015-02-10
基金项目:国家自然科学基金资助项目(51008196);上海市一流学科项目(S1201YLXK)
作者简介:汪圣伟(1990—),男,安徽省广德县人,上海理工大学硕士研究生,主要研究方向为智能交通系统、交通运输规划与管理;韩印(1964—),男,黑龙江省绥化市人,上海理工大学教授,博士生导师,主要研究方向为智能交通系统、公交优先控制。
随着城市的发展,城市交通流量日益剧增,城市道路网密度也逐渐增加,交叉口作为交通流改变流向的地点,相邻交叉口之间的关联性也更加明显,交叉口扮演着重要的角色,对路网中交叉口群的研究也越来越受到人们的重视。因此对网络交叉口群进行子区域划分,采用区域协调控制越来越受到国内外学者的关注。
Yagoda等[1]认为交叉口之间的关联性主要与路段上的流量和路段长度有关。Pinnell等[2]认为影响相邻交叉口关联性的因素包括路段长度、上游交叉口车流量及其到达规律。卢凯等[3]在分析影响交叉口关联性因素的基础上提出了多交叉口组合关联度的计算公式,并研究了干线系统交叉口群的子区域划分方法。保丽霞[4]基于车队离子散模型提出了综合反映交叉口影响因素的量化公式。杨洁等[5]建立了路径关联度模型来确定协调控制对象,并进行了实例分析比较协调控制前后的交通运行效率。马万经等[6]提出了基于路径信号控制交叉口关联度计算模型,并进行了算例分析。胡华等[7]提出考虑路网OD路径的交叉口动态划分方法。就目前而言,这些研究大多集中于对影响相邻交叉口之间的关联性要素的分析,或者路径关联性等方面的研究,缺少进行仿真分析,以及从网络交叉口群间关联性的角度进行交叉口群划分的研究。本文在此基础上提出网络交叉口群间关联性的计算方法,并进行子区域划分,为进行网络交叉口群协调控制提供了一种新的有效的依据。
1相邻交叉口关联性影响要素分析
车流从上游交叉口以高密度、紧凑的状态,伴随着离散现象,以低密度、随机的形式达到下游交叉口,为了反映这种交通流的运行状态的改变程度,引入交叉口关联性这一定义。由此可以看出对于影响交叉口关联性的因素,主要有交叉口间距、路段流量、信号配时参数等。
1.1交叉口距离
交叉口距离作为静态影响因素,在实际生活中一般情况下是不容易发生改变的。当两交叉口间的距离过长的时候,上游交叉口驶出的车流,会随着距离的拉长,车头时距会改变,最终以随机的车流达到下游交叉口,表现为弱相关性;当交叉口间的距离较短的时候,从上游驶出的车流很大程度上保持原有的车队驶入下游交叉口,表现为强相关性。同时,过长的交叉口距离也会降低下游排队车辆对于上游驶出车辆的影响,同样表现为弱相关性。因此距离越长,相关性越弱。
1.2路段流量
路段流量作为一个关键因素,直接影响交叉口间的关联性,因为最终都是通过车流的改变程度来判断。当流量较大,饱和度较高,上游交叉口的驶出车流也会更加密集,同时车队长度也会更长,路段可容纳剩余交通量越少,更不容易发生离散现象;相反,当饱和度较低,车流随机性更大,路段剩余可容纳交通量越多,更容易发生离散现象。因此路段交通量越多,相邻交叉口关联性越强。
1.3周期比
信号配时对交叉口关联性的影响最主要集中在周期比,相位差,绿信比等参数。相位差可以通过直接分析两交叉口间的行驶时间来大致确定。在这里我们主要分析周期比。对于相邻交叉口采用协调控制而言,必须保持相等的信号周期时长和一定的相位差,使得上游交叉口输出车流能够更加顺利的通过下游交叉口。因此当周期时长相等或者成整数倍时,车流往往会按照原来的状态顺利通过交叉口,不需要进行排队等候。当周期时长差异较大,表现为车流容易受阻。因此当周期比为整数时,表现为强相关性,差异较大时表现为弱相关性。
2相邻交叉口关联性分析
2.1相邻交叉口关联度
相邻交叉口关联度是关于以上三个影响因素的综合反映,不能单纯的考虑其中某一个因素的影响。文献[8]Whitson模型中,耦合得到交叉口关联性的量化指标为:
(1)

(2)
其中I(i-j)为交叉口i至交叉口j的关联度,Na为上游交叉口驶出车辆数,Nb到达下游交叉口车辆数,Nc为下游交叉口排队车辆数,gi为绿灯持续时长,KL为单个车辆平均长度,取3.8 m,L为交叉口间距,Kp为信号配时修正系数。
在VISSIM仿真中,驶出驶入和排队车辆数都可以通过设置数据采集点采集得到,交叉口间距也可以方便设置。
为了简化处理,在每次仿真中,将相位差直接使用交叉口距离L除以平均车速V得到的行驶时间替代,并且将绿信比定义相同,参考卢凯在相邻交叉口关联度分析及其应用中周期关联度的定义[3],考虑周期比对关联度的影响就可以定义信号配时修正系数如下:
(3)
其中Tmax和Tmin分别为相邻交叉口信号周期的最大值和最小值。
2.2仿真结果分析
在VISSIM中建立路网,进口道都设置为3车道,分别为左转、直行、右转专用道,通行能力分别设为800,1 200,1 000 pcu/h。采用常用四相位信号控制策略,初始周期时长都设为100 s。绿信比按照流量比的方法进行分配,得到仿真路网如图1所示。

图1 仿真路网示意图
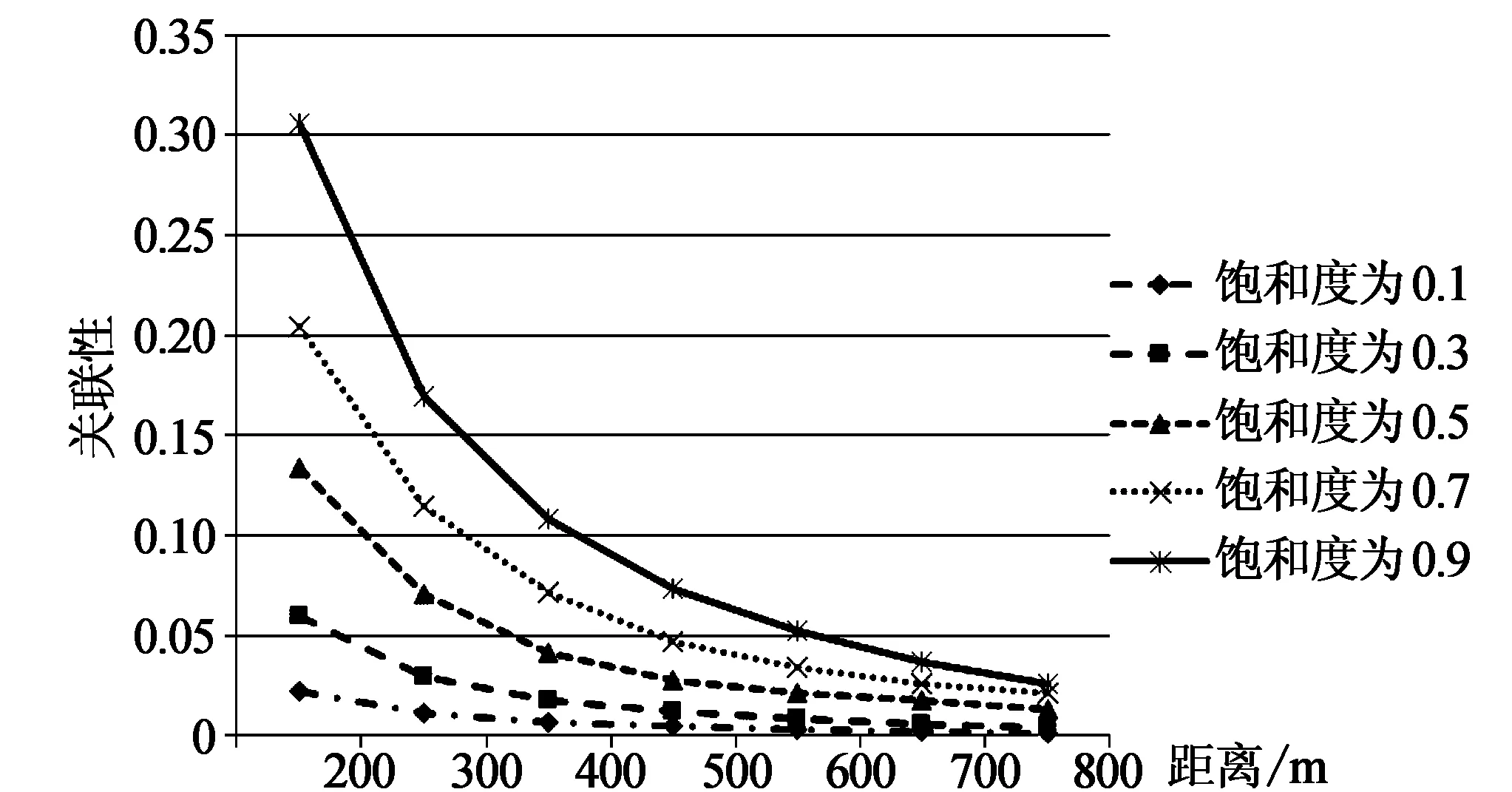
图2 距离与饱和度对交叉口关联性影响

图3 周期比对交叉口关联度的影响图示
由于刚开始仿真的不稳定性,因此每次仿真采集500 s以后相同的仿真时长。在不断改变距离和饱和度的情况下,每次统计10次仿真结果取平均值,并计算I(i-j)值,得到在信号配时相同情况下距离与饱和度对交叉口关联度影响如图2所示。
从图中可以看出,当距离越小时,饱和度对交叉口的关联性影响越大;在饱和度越小的情况下,距离对交叉口关联性的影响也越小。在现实生活中,交叉口之间的距离往往是确定的,当交叉口i的饱和度达到一定程度的时候就可以做单向交叉口i与j的协调控制,同理也可以判断j对i协调控制,当两者都满足条件就可以进行双向协调控制。
由于设置了相位差和绿信比,因此只考虑在改变周期比的情况下,对交叉口关联性的影响。取最接近实际的交叉口饱和度为0.7,交叉口距离为700 m的情况下[4],分别调整i与j的周期比,然后将得到的交叉口关联度I(i-j)压缩至0到1之间,取比值为1时I(i-j)也为1处理,得到如图3所示。
从图中可以看出,当周期比处于整数倍的时候就会出现峰值,适合进行协调控制,其他比值的效果不明显。从信号配时修正系数Kp中也可以看出这种趋势。
3网络交叉口群关联性的交叉口群划分方法
3.1网络交叉口群交叉口关联性分析
目前国内外对交叉口关联性的研究大多集中在相邻交叉口或者干线交叉口群,缺少对网络交叉口群的关注。但是现实中不可能存在两个孤立的交叉口,并且单独计算两个相邻交叉口之间关联性的大小不具有参照性,因此在网络交叉口群中分析相邻交叉口之间的关联度就非常重要。在分析之前首先做如下假设:
(1)前面已经提到对于相邻交叉口关联度的度量参数I(i-j),需要注意的是,由于交叉口i与j之间相互影响程度不一样,因此I(i-j)与I(j-i)并不相同。
(2)与交叉口i相连接的交叉口是有限个。
(3)从路段中间进出路网的流量可以忽略不计。
基于以上假设的基础上,分析得到车流从交叉口i分散行驶至与其相连的交叉口,各个方向的流量,信号配时差异等等都不相同,但是交叉口i与有限个相关联的交叉口相邻,因此可以定义在网络交叉口群中交叉口i和与之相连接的若干个交叉口之间存在如下关系:
(4)
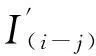
(5)
进一步得到定义网络交叉口群中交叉口关联性:
(6)
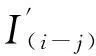
3.2网络交叉口群划分方法研究
基于上述分析的基础上提出网络交叉口群子区域划分方法:
(1)搜索全网络,当相邻交叉口i与j之间的关联度D(i-j)小于相邻交叉口分离阀值Ds,交叉口i与j必须分离在不同的子区域中。
(2)搜索全网络,当相邻交叉口i与j之间的关联度D(i-j)大于相邻交叉口合并阀值Dt,交叉口i与j必须划分在同一个子区域中。
(3)对于处于Ds和Dt之间的关联度,求得网络多交叉口关联性为:
(7)
以此类推,连乘求得当D(i,j,k,m)小于相邻交叉口分离阀值则划分为不同的子区域中,否则以网络多交叉口关联性D(i,j,k,m)最大为判别原则,合并到已经存在的子区域中。
(4)搜索全网络,对于剩下不能合并的交叉口单独划分为一个子区域。
对于划分在同一个子区域的交叉口群就有利于进行区域协调控制,提高交通运行效率。
4案例分析
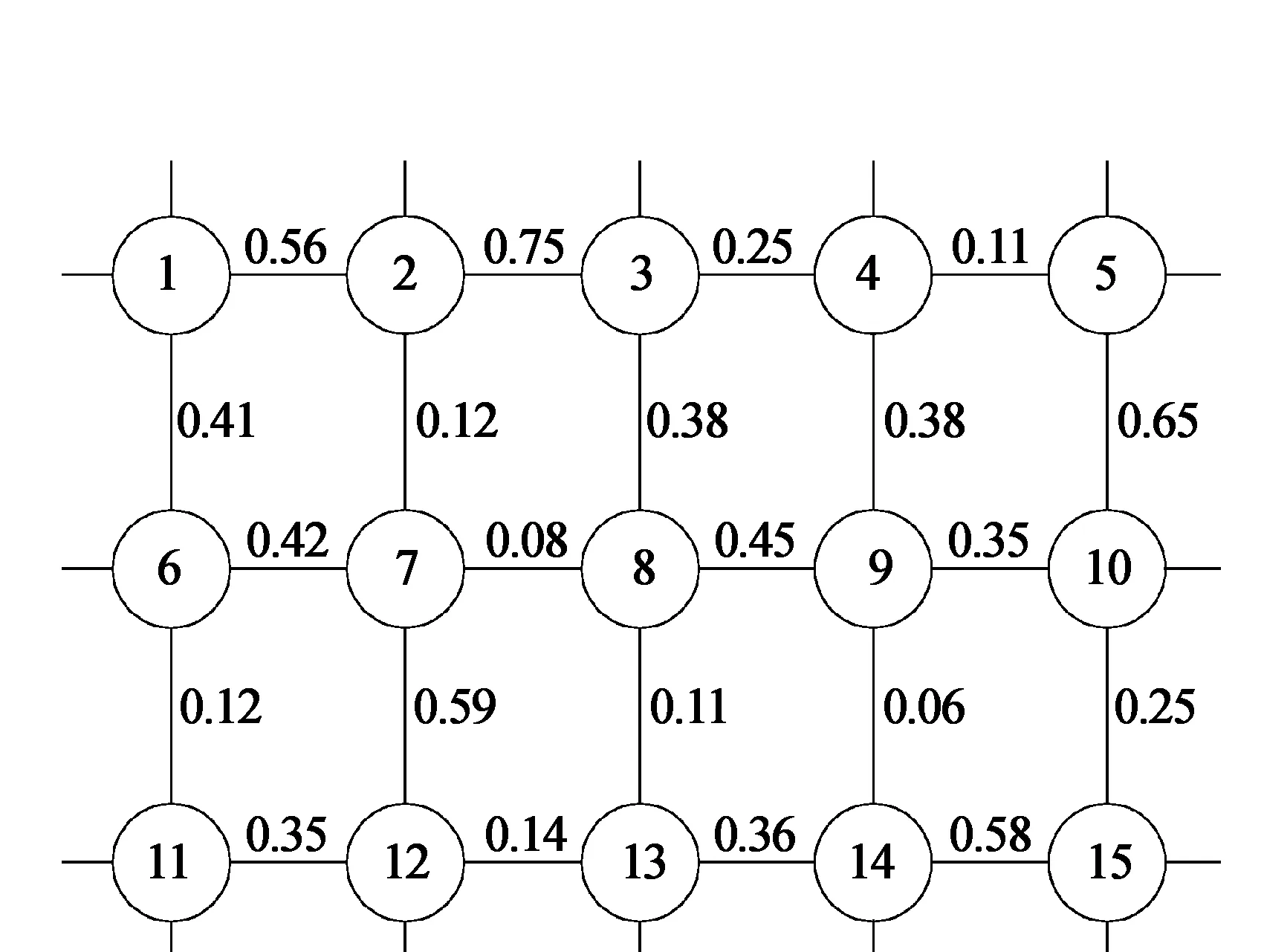
图4 网络交叉口群关联性图示
如图4所示为一个由15个交叉口组成的网络交叉口群,分别标号1—15,图中给出了交叉口之间关联性的值。文献[9]给出了相邻交叉口划分的分离和合并阀值Ds,Dt分别为0.15和0.5。
首先从第一和第二条原则进行划分,其中(1,2,3),(5,10),(7,12),(14,15)划分为一个子区域,(2,7),(4,5),(7,8),(6,11),(12,13),(8,13),(9,14)分开为不同的子区域中,结果如图5所示。
考虑与(1,2,3)交叉口群相连接的4,6,8交叉口,分别连乘计算其网络多交叉口关联性,取其中最大且大于Ds的考虑合并为一个子区域,得到(1,2,3,6),但是6同时与(7,12)相连接,比较(1,2,3,6)和(6,7,12),得到多交叉口关联性(6,7,12)大于(1,2,3,6)且大于(7,12,11),最后合并(6,7,12),(1,2,3,8),11不能与(6,7,12)合并,4与9也不能合并到(1,2,3,8)中;考虑与(5,10)相连接的9和(14,15),分别计算其网络多交叉口关联性最后得到(5,10,9)合并为一个子区域,计算与(5,10,9)相连接的4和8都不能合并;采用相同的方法得到(13,14,15);取剩下的交叉口单独划分为一个子区域,最终结果如图6所示。
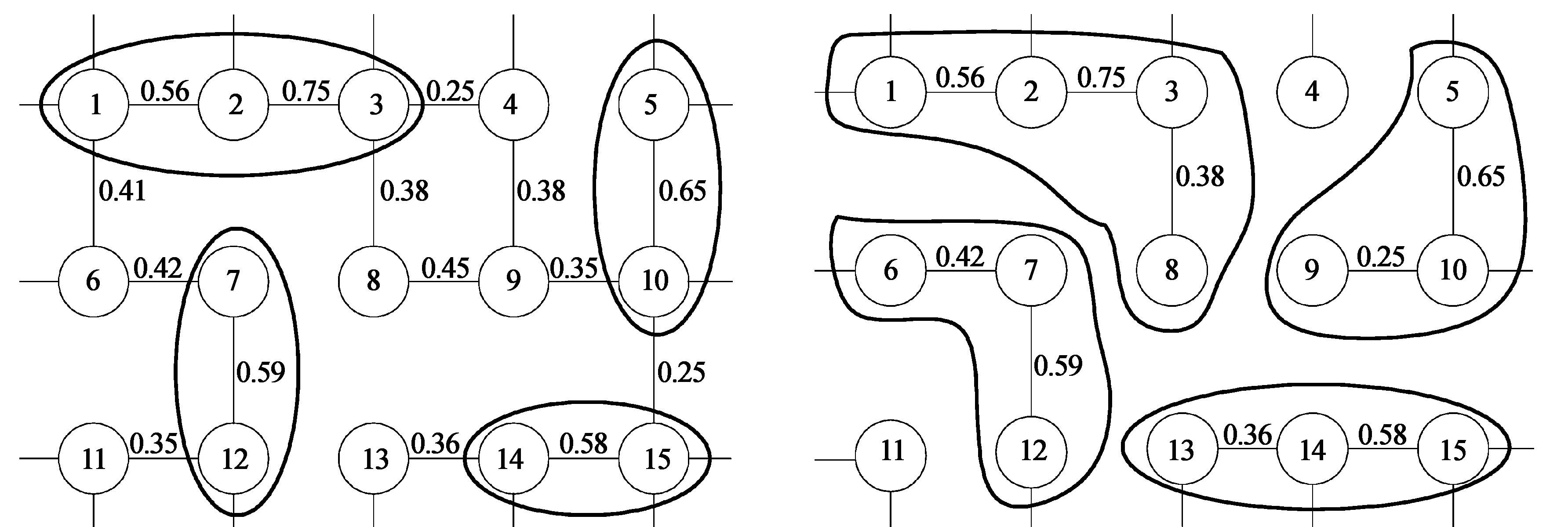
图5 首次划分示意图 图6 交叉口群子区域最终划分示意图
5结束语
通过对影响相邻交叉口关联度的因素的分析,提出了综合考虑各因素的相邻交叉口关联度计算公式,并通过仿真验证了计算公式的合理性。在此基础上提出了网络交叉口群交叉口关联度的计算方法,并提出进行网络交叉口群的子区域划分的原则,然后进行案例分析解释说明这种模型方法的用处,证明这种方法的适用性,为以后进行子区域划分乃至区域协调控制奠定了一定的基础。
但是,仿真存在一定的不准确性,而且简化了相位差和绿信比对相邻交叉口关联性的影响;对交叉口群关联性分析中,是在相邻交叉口关联性的基础上间接的提出,而没有直接从网络交叉口群中分析他们之间的关系,因此还有待于后续进一步的研究。
[参考文献]
[1]YAGODA H N,PRINCIPE E H,VICK C E,et al.Sub division of signal systems into control areas[J].Traffic Engineering,1973,43(12):42-45.
[2]PINNELL C.Area wide traffic control systems[J].Traffic Engineering & Control,1975,45(4):16-21.
[3]卢凯,徐建闽,郑淑鉴.相邻交叉口关联度分析及其应用[J].华南理工大学学报:自然科学版,2009,37(11):38-42.
[4]保丽霞.基于车队离散模型的交叉口关联度量化方法研究与实验[J].公路交通科技,2011,28(s1):1-8.
[5]杨洁,过秀成,李岩,等.城市信号控制交叉口路径关联度模型[J].交通运输系统工程与信息,2012,12(1):56-62.
[6]马万经,李晓丹,杨晓光.基于路径的信号控制交叉口关联度计算模型[J].同济大学学报:自然科学版,2009,37(11):1474-1467.
[7]胡华,高云峰,杨晓光.考虑路网OD路径的交叉口群动态划分方法[J].计算机工程与应用,2010,46(31):1-4.
[8]ROBERT L G,WARREN T.Traffic control systems handbook[R].Washington:Department of Transportation Federal Highway Administration,2005.
[9]美国运输部联邦公路局.交通控制系统手册[M].李海渊,秦吉玛,王彦卿,译.北京:人民交通出版社,1987:69-71.
[10]胡兴丽.小区域交叉口群的优化控制方法研究[J].重庆:重庆交通大学,2013.
[11]胡华,高云峰,邱薇华.基于路径关联性的交叉口群动态划分方法[J].重庆交通大学学报:自然科学版,2010,29(5):758-762.
[12]李岩,杨洁,过秀成,等.基于小波变换的关联交叉口群关键路径识别方法[J].中国公路学报,2012,25(1):135-140.
[责任编辑:张存凤]
Study of the relevance of intersection-groups in transportation network
WANG Sheng-wei,HAN Yin
(Business School, University of Shanghai for Science and Technology, Shanghai 200093, China)
Abstract:In the operation of urban traffic, intersections play an very important role, and the study for intersection-groups in transportation network is gaining more and more attention. Firstly, by analyzing the impact of intersection distance, link volume and cycle ratio on the relevance of adjacent intersections, a new traffic metrics is proposed to describe the relevance of adjacent intersections quantitatively. Then through the simulation method, the quantitative metrics is verified to be reasonable, and furthermore a new calculation method which reflects the relevance of intersections in transportation networks and the corresponding dividing principles of intersection-groups are suggested. A case analysis is conducted to prove the usage of these new principles, which provides a reliable approach to sub-regional division of intersection-groups in transportation network.
Key words:urban traffic;sub-regional division of intersection-groups;relevance of intersection-groups in transportation network;intersection-groups;relevance of adjacent intersections

