浅析如何利用概率论提高投标率

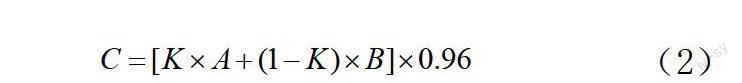
摘要：在进行投标时，建立一套合理的报价决策方法是提高投标报价决策成功率的重点。文章通过对竞争对手进行分析，然后利用评标方法分析概率降低人为因素对投标的影响，以提升报价决策的合理性。

关键词：概率论；投标率；报价决策方法；评标方法；工程成本 文献标识码：A

中图分类号：TU732 文章编号：1009-2374（2016）03-0184-02 DOI：10.13535/j.cnki.11-4406/n.2016.03.094

企业在投标时，报价决策的合理性对投标结果有较大的影响。而投标人员凭借自己的感觉和经验进行投标会具有一定的随机性和盲目性。制定合理的报价决策方法可以有效地提高报价的成功率。为了提高报价决策的科学性，需要对企业的工程成本进行测算，对竞争对手以往的投标情况进行分析，建立一套合理的数学模型，然后利用计算机将这一过程实现。

1 工程概况

本标段起于泉南高速宁都县赖村镇附近的宁都南互通立交，跨过国道319向南，经蒙坊村、在何包圩村跨乡道Y511、在中田坑水库东侧设中田坑水库大桥，后经大岭背、上浮竹、下浮竹、冷水坑，在K13+464进入到于都县葛坳乡曾子村，在现有潭步桥下游设青塘河大桥跨青塘河，后经仙坛背、龙虎岭，设杨梅村大桥跨越乡道Y543后到达标段终点，全长18.9km，为双向四车道高速公路，设计行车速度为80km/h，整体式路基宽24.5m，分离式路基宽度12.5m，设计荷载为公路-Ⅰ级。

2 概率分析的基本原理

概率分析又叫做风险分析，是在不确定因素的情况下，对经济效益指标的风险度和期望值进行分析和计算的一种方法。在一些方案中一部分参数无法确定，但是知道参数的概率范围时，可以对其概率进行分析。在进行概率分析时，首先要将影响项目决策的不确定因素确定出来，并假设各个因素是互相独立的，然后将所有影响这些因素的概率和取值确定出来，利用大量的数据资料、历史资料等将概率分布确定出来。分析各个状态下的概率值，然后对各个指标的期望值进行评价。

式中：评价指标指的是X，评价指标下X第i中可能状态为，评价指标X第i种可能状态概率为，n指的是X的可能状态数，评价指标X第i种可能状态概率为Pi。

3 合理低价法对提高中标率的影响

合理低价中标指的是由评标委员会经过会审认定的中标价，可以保证工程项目在保证最低的报价的同时，得到最为合理、科学的施工报价。在招标过程中，使用合理低价法可以有效降低工程投资，控制腐败，避免出现陪标和围标情况。本项目使用设定评标基准价的方法进行计算，分别从各个标段中随意抽出一种方法作为此标段计算评标基准价的方法。主要有以下四种：（1）二次平均法。对所有参与评标基准的评标价进行第一次平均，然后对所有等于或者低于第一次平均值的平标价进行二次平均，第二次计算出来的平均值就为评标基准价P；（2）不距随机法。评标基准价P=（Emax-Emin）×K+Emin，其中Emin指的是去掉n2個最低评标价后的最小值，Emax指的是去掉n1个最高评标价后的最大值，K指的是基准系数，分别从现场提取X、Y两个系数组成，K=（X+Y）/10，其中X有十个系数，分别为0、1、2、3、4、5、6、7、8、9，Y的十个系数分别为0、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9；（3）权重随机法。P=A×K+B×（1-K）A，P指的是去掉n1个最高评价后的最大值。K指的是权重系数，B指的是参与评标基准计算的所有评标价平均值；（4）随机低价法。适合N大于等于5的时候使用，P指的是去掉n个最低平标价的最低价，n是从开标现场随意抽取的数值，处于n3～n4，步距等于1，n3=N×0.2，N4=N×0.7，n3和n4向下取整。在整个评审过程中，评标基准价要保持一致，不因报价文件评审投标人的变化而变化。偏差类=100%×（投标人投标报价-评标基准价）/评标基准价，偏差率保留到小数点九位以后。

4 概率理论在项目中的应用

项目招标过程中，C为评标基础，使用式（2）进行计算：

在式（2）中，最高限价为A，投标人的投标报价（bi）有效范围内（0.92A设投标人的总数为N，一般情况下N为3～7个，那么投标人的报价也需要保持在有效的范围中，也就是。因此，先假定每一投标人都是在0.92A～A之间用同样概率来随机进行报价{b1，b2，…bi，…bN}，其中第i个投标人的报价用来表示，那么就有：

B={b1，b2，…bi，…bN}/N （3）

将式（3）代入到式（1）中计算，得出C值，然后求出C值的概率分布情况，进而合理地选择投标报价，提升中标率。可以随机多次抽取m组{b1，b2，…bi，…bN}，然后计算出m个C值，统计m值的分布情况，计算出C概率分布图。例如N=5、k=0.3时，A为1万元，那么bi从0.92～1的范围中进行取值。随机选取六组投标报价如下：

使用式（1）和式（3）进行计算，求出：，因为0.92A

其他区间数目为0，统计次数越多，所求得的C值概率分布精确度越高。在计算C的概率分布时，需要使用到以下参数：统计次数m为100，A为1万元时，bi的取值范围为0.92～1万元。取投标人数为5，那么就有k=0.1，0.15，0.2，0.25，0.3。

第一，当k=0.1时，0.8909A第二，在k=0.15时，C处于0.8947A～0.9600A之间，C的总区间范围为0.8900≤Cx≤0.9600。经过分析证明，当评标基数C位于区间0.9260～0.9280之间时，C=23，数量最多。因此，将投标率报价确定在0.9260A～0.9280A之间时，最有可能中标。而投标报价处于0.9440A～0.9600A（26～35区间）时，会影响中标率。

第三，在k=0.2时，C处于0.8986A～0.9600A之間C的总区间范围为0.8900≤Cx≤0.9600。经过分析证明，当评标基础位于0.9280～0.9320范围中，即C区间20和21时，C=24，数量最多，因此，将投标报价控制在0.9280A～0.9320A之间时，最有可能中标，而将投标报价控制住在0.9440A～0.9600A时（26～35），中标概率较低。

第四，当K=0.25时，C处于0.9024A～0.9600A之间，C的总区间范围为0.9000≤Cx≤0.9600，区间0.9000～0.9020，0.9020～0.9040，0.9040～0.9060，…0.9580～0.9600 顺次为1，2，3，…，30，那么第S（1≤s≤30）个区间为[0.9000+0.002×（s-1）]～[0.9000+0.002×s]。在进行200次随机抽样、统计和计算后，得出如下结果：当评标基础位于0.9300～0.9320内（区间16），C=31，数量最多。在进行投标时，将报价控制在0.9300A～0.9320A的范围时，最可能中标。而将投标报价控制在0.9400A～0.9600A时（区间21～30），中标率不高。

第五，当k=0.3时，C处于0.9062A～0.9600A之间，C的总区间范围为0.9000≤Cx≤0.9600，根据计算结果可以看出，当评标基数保持在0.9320～0.9340（区间17）时，C=27，数量最多。因此，投标报价在0.9320～0.9340时，最有可能中标，而当投标报价处于0.9380A～0.9600A（区间22～30）时，中标概率最小。

5 结语

项目投标过程中，以随机抽取K值的具体情况，不能得到准确的报价范围。所以将K取值情况看作一个综合统计，投标报价范围控制在0.9240A～0.9340A时，可以全面提高中标率。上文中评标基数C值概率分布结果是在进行多次的抽样、统计、计算后得到的，计算结果和统计学相符合，不过在实际应用过程中，计算结果是只能作为投标参考。此外，根据理论分析结果不难看出，投标人的数量越多，评标基数C会更集中分布。出现这种情况主要是因为投标人数量增加时，投标人报价算术水平会越来越靠近0.9200～0.9600的中间值，可以更加准确地将投标最佳报价范围确定出来。另外，为了进一步提升评标基数概率的分布情况，可以做好以往类似工程的报价统计工作，将投标报价的分布概率计算出来，从而帮助我们提升工程投标的中标概率。

参考文献

[1] 李亚兰.在概率论习题教学中加强学生创新思维能力[J].高等函授学报，2014，（2）.

[2] 华中科技大学数学系.概率论与数理统计（第二版）[M].北京：高等教育出版社，2003.

[3] 林伟生.建设工程招标投标规范化管理策略研究[D].重庆大学，2005.

作者简介：贾娜（1980-），女，河北辛集人，中铁十五局集团第五工程有限公司工程师，研究方向：工程造价。

（责任编辑：王 波）