旋风分离器内气相湍流流动的数值模拟

唐守强，沈玉凤，王　辰

(山东理工大学 交通与车辆工程学院，山东 淄博 255049)

旋风分离器内气相湍流流动的数值模拟

唐守强，沈玉凤，王辰

(山东理工大学 交通与车辆工程学院，山东 淄博 255049)

摘要：采用标准k-ε模型、雷诺应力模型(RSM)以及k-w模型对旋风分离器内部湍流流场进行了数值模拟.对比了采用两种不同的离散格式时的计算表现，分析了不同近壁模型对于模拟结果的影响.通过数值解与实验值进行的对比发现采用雷诺应力模型较k-w模型，k-ε模型能更准确地模拟分离器内强旋流场.

关键词：旋风分离器；湍流模型；数值模拟

收稿日期：2015-01-16

通信作者：

作者简介:唐守强，男，tangshouqiang001@163.com;沈玉凤，女，syf100@sdut.edu.cn

文章编号：1672-6197(2016)01-0067-06

中图分类号：TQ051.8； O35； X701； TB126

文献标志码：A

Abstract:Numerical simulation of swirling flow in a cyclone separator was conducted using standard k-ε model, Reynolds stress model (RSM) and k-w model.The performances of using two convective term discretization schemes and variant near wall treatments were also studied in present investigation. It was found that the numerical results predicted by using RSM were closer to the experimental data than those results predicted by using standard k-ε and k-w models.

Numerical simulation of gas-phase turbulent flow in cyclone separator

TANG Shou-qiang, SHEN Yu-feng, WANG Chen

(School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo 255049, China)

Key words: cyclone separator; turbulent model; numerical simulation

旋风分离器作为一种烟尘净化装置，由于其结构简单、无相对运动部件等特点[1]，被广泛应用在煤炭发电、石油化工和环境保护等许多行业.在旋风分离器的工作过程中，含尘气体从入口进入分离器内部后，由直线运动转化为圆周运动.此时，气体中的颗粒因为旋转运动而受到离心力，部分颗粒会被甩向壁面，通过与壁面的碰撞，动能减少，进而落入排尘口而被分离出来.由于旋风分离器内部流动的复杂性，在利用计算流体力学软件对其进行模拟时，还没有一种公认的模拟方法[2].本文利用CFD软件,使用标准 k-ε模型、k-w模型和雷诺应力模型(RSM)计算旋风分离器中的气相流场，并同实验值进行比较，以期选取一种最佳的湍流模型，确定最适合于旋风分离器内部流场的计算方法，为今后旋风分离器中气固两相湍流的模拟工作提供一定的基础.

1物理模型

本文计算的旋风分离器模型和结构尺寸与文献[3]中的旋风分离器模型相同，其几何尺寸如图1所示，其具体参数如下：D=190mm，H=760mm，h=285mm，a=95mm，b=38mm，c=190mm，B=72.5mm，De=64mm，S=95mm，t=145mm.

采用ANSYS ICEM—CFD软件划分网格，将旋风分离器分为入口、上出口、下出口、壁面等4个部分.采用六面体结构网格，并划分了边界层.根据旋风分离器的结构，划分出了3层O-Block，网格总数为50万，网格划分结果如图2所示.

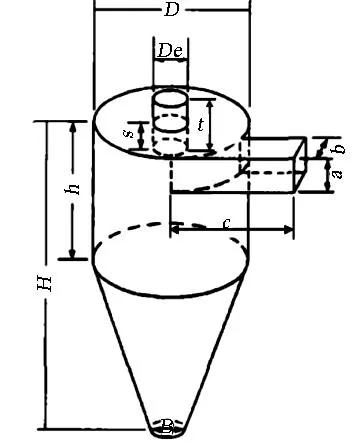
图1旋风分离器结构图

图2旋风分离器网格划分

2湍流模型

Fluent在求解流体运动问题时，直接求解N-S方程太过困难.目前，最常用的解决方法是采用雷诺平均法，对方程取时间平均后求解.这样，就引入了新的变量——雷诺应力.根据对雷诺应力的假定和处理方式不同，产生了不同的湍流模型.

2.1　标准k-ε模型

湍动能k和湍流耗散率ε的输运方程[4]为

(1)

(2)

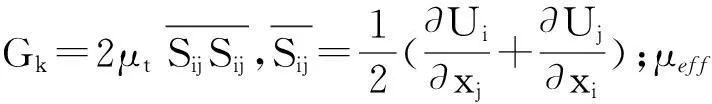
2.2　 k-w模型

湍动能k和比耗散率w的输运方程为：

(3)

(4)

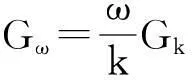
2.3　雷诺应力模型

雷诺应力各分量的输运方程为

Gi,j+Φi,j+Fi,j+Suser-εi,j

(5)

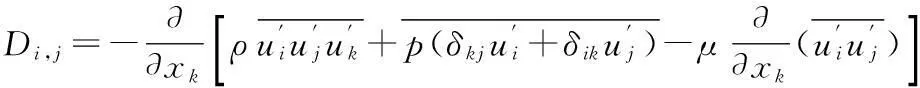
经模拟化，湍动能方程和湍动能耗散方程变为

(6)

(7)

3数值计算条件的设置

3.1　边界条件

(1)入口条件：气体采用常温下的空气，入口设置为速度入口(Velocity-inlet)，进口气速为7.5m/s.在湍流参数的制定方法中，设置湍流强度为5.5%，水力直径为54.29mm.

(2)出口条件：排气管出口为自由出流(Outflow)，流量加权比例设置为1.排尘出口为自由出流(Outflow)，流量加权比例设置为0.

(3)壁面条件：固体壁面为无滑移条件.

3.2　数值计算方法

本文采用有限体积法对各控制方程进行离散，模型的数值求解算法采用非交错网格的SIMPLEC算法[5]，压力梯度项的插补采用PRESTO格式，同时利用二阶迎风格式或一阶迎风格式对旋风分离器内流场进行数值模拟.

4模拟结果与分析

4.1　不同湍流模型的模拟结果比较

4.1.1　切向速度分布

旋风分离器内部的流场具有较明显的特点，已经有大量的实验结果[6]表明：旋风分离器内部的切速度呈现出典型的兰金涡结构[7]，包括外部的准自由涡和内部的强制涡.其中外部的准自由涡向旋风分离器下方旋转，为下行流.内部的强制涡向上旋转，为上行流.在两部分的交界面处切向速度最大.

图3为不同湍流模型在旋风分离器不同高度处，沿筒体半径方向r的切向速度分布图，并与实验值进行了对比.其离散格式均为二阶迎风格式.模型的坐标原点设置为排尘口中心处，z轴正方向设置为沿着分离器中心轴线向上.从图3可以看出：k-ε模型中，切速度随着半径r的增大而一直呈现增大的趋势，没有能够反映出旋风分离器内部的兰金涡结构.k-w模型中，切向速度呈现先增大后减小的趋势，较之k-ε模型，模拟的准确性有所提高，流动可以分为内部流和外部流两部分，存在切向速度最大的一个分界面.但是其最大切速度的位置与实验值相比，差距较大.所以，也没有能够反映出旋风分离器的真实切速度分布规律.雷诺应力模型(RSM)与实验值相比，基本反映出了分离器内部切速度的流动特征，并且切向速度的值与实验值吻合程度也较好，最大切向速度界面的位置也基本一致.

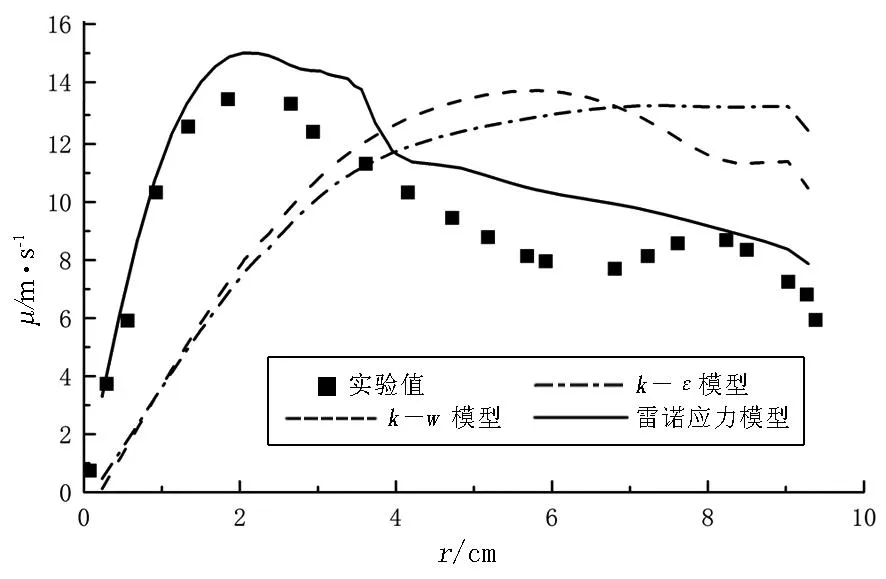
(a)z=645mm

(b)z=635mm

(c)z=610mm

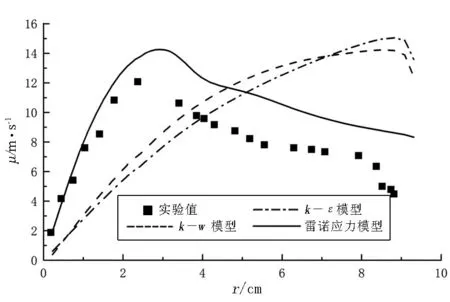
(d)z=560mm

图3不同湍流模型的切向速度分布

(a) k-ε模型

(b) k-w模型

(c) 雷诺应力模型图4　不同湍流模型的切向速度云图

图4 给出了3种不同湍流模型在x=0截面的切向速度分布云图.其中速度方向以逆时针为正，实际流动过程中大部分的气体流动为顺时针方向，故大部分速度值为负数.从图4(a)可以看出：k-ε模型中，由中心向外的切向速度一直呈现增大的趋势，不符合实际情况.从图4(b)中可以看出：k-w模型的切向速度值存在一个最大的界面，但此界面较

靠近壁面，并呈现不规则的分布，与真实的流动情况不符.从图4(c)中可以清晰的看到一个最大切向速度的面，将气体流动分为了内部和外部两个部分.并且此面基本处在排气管的延长面上.这与大量已有的实验结果[6]相一致，故通过云图比较可以看出：使用雷诺应力模型(RSM)模拟的旋风分离器内部切向速度更符合现实情况.

4.1.2　轴向速度分布

图5 为不同湍流模型轴向速度的比较.从图5中可以看出：在半径r=0~3cm的范围内，k-w模型，k-ε模型的模拟值都不能很好的与实验值吻合，模拟的速度值比实验值小.而雷诺应力模型(RSM)在整个范围内与实验值的吻合程度较高，较准确地反映了旋风分离器轴向速度的分布规律.

综合切向速度和轴向速度值的比较，可以得出结论：3种湍流模型中，基于各向同性的k-ε模型和k-w模型不能够应用于强旋流的模拟，而基于各向异性[8]的雷诺应力模型(RSM)能够反映出旋风分离器内部流场的实际情况，可用于进行流场的计算.

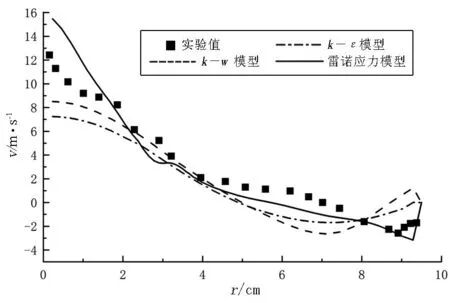
(a)z=645mm

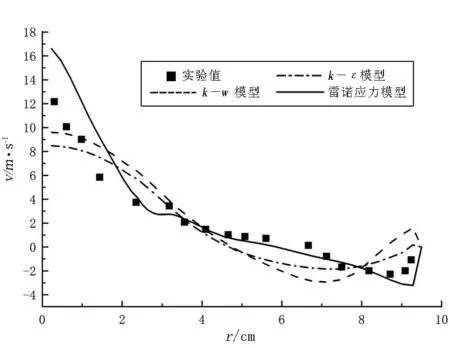
(b)z=635mm

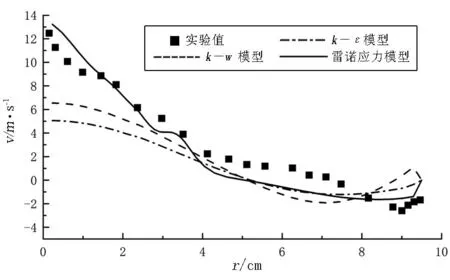
(c)z=610mm

(d)z=560mm

图5不同湍流模型的轴向速度分布

4.2　不同离散格式的比较

在对流场进行数值模拟时，需要对流场的控制方程进行离散，只有选择了合适的离散格式，才能够得到准确并且稳定的计算结果.图6 比较了使用一阶迎风差分格式和二阶迎风差分格式进行模拟运算时，流场内的速度值，并与实验值进行了对比，其中湍流模型使用雷诺应力模型.

由图6可以看出，尽管一阶迎风格式的收敛性较好，但是它的模拟结果与实验值差别很大，产生了较大的误差.故一阶格式不能有效反映出旋风分离器内部的流动情况.二阶迎风格式的模拟结果反映出了分离器内部的基本特征，并且速度大小与实验值基本相同.故可以得出结论：一阶迎风格式不可用于旋风分离器的模拟计算，二阶迎风格式能够较准确地反映旋风分离器内部的流动情况，可用于计算旋风分离器的内部流场.

4.3　近壁面处理方法对模拟的影响.

Fluent中提供了多种不同的近壁面处理方法，如标准壁面函数法、可依比例缩放的壁面函数法、非平衡的壁面函数法.

图7对3种近壁处理方法进行了对比.在雷诺应力模型下，使用二阶离散格式进行了模拟.由图7可以看出，3种壁面函数都能较准确地反映旋风分离器流场的外部准自由涡和内部强制涡等特点，只是最大切速度值所在的位置稍有不同.通过切向速度和轴向速度的比较可以看出，3种近壁面模型的模拟结果差别不大.由图7(a)看出：在z=645mm截面处，非平衡的壁面函数法和标准壁法函数法的切速度模拟结果基本相同，比可依比例缩放的壁面函数法的结果更加符合实验值.由图7(b)看出：在z=610mm截面处，非平衡的壁面函数法比其它两种方法的切速度模拟结果更加准确.从图7(c)z=645mm处轴速度比较中发现：非平衡的壁面函数法比其它两种方法效果要好.唯独在图7(d)z=610mm处轴速度比较的r=1~4cm一段,非平衡的壁面函数法较之其它两种方法略有失真.故总体上看，使用非平衡的壁面函数法最能够反映旋风分离器内部的流动情况.

(a)z=645mm处切向速度对比

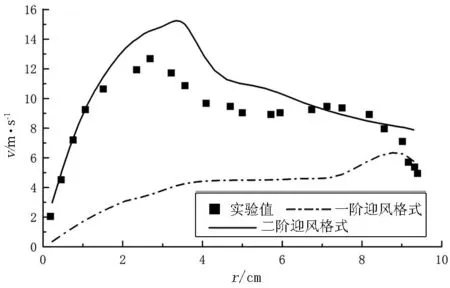
(b)z=610mm处切向速度对比

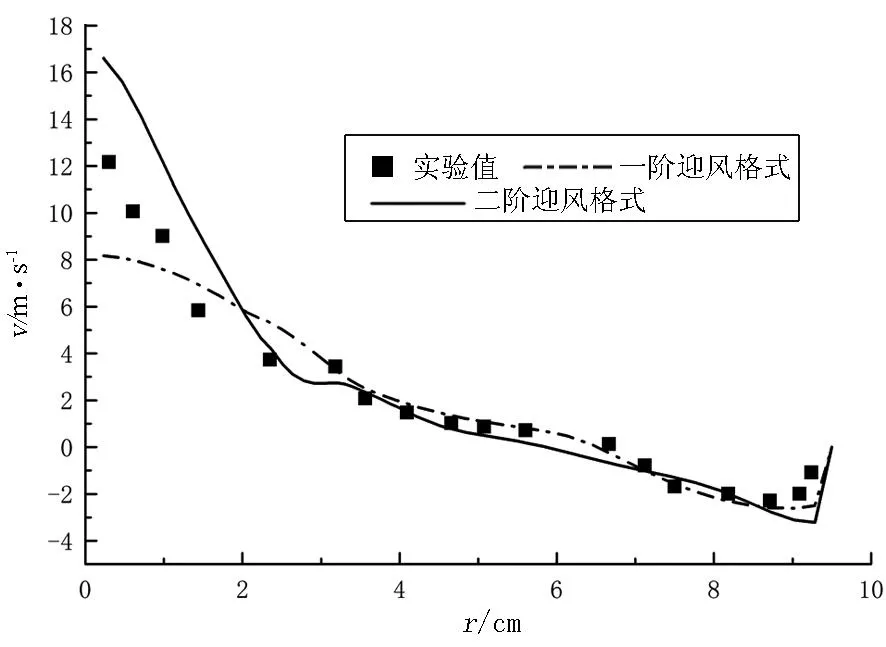
(c)z=645mm处轴向速度对比

(d)z=560mm处轴向速度对比

图6不同离散格式的速度分布对比

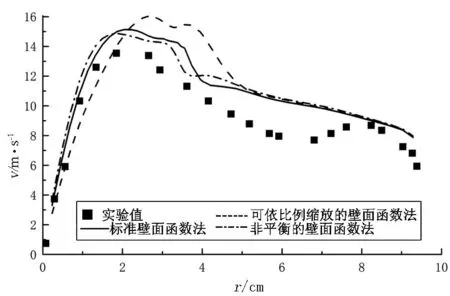
(a)z=645mm处切向速度对比

(b)z=610mm处切向速度对比

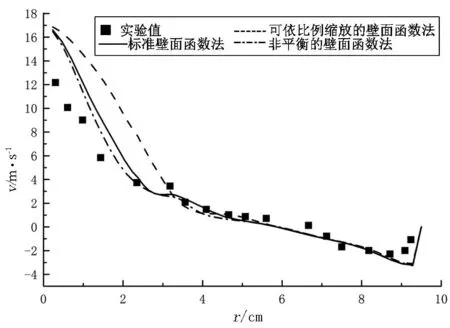
(c)z=645mm处轴向速度对比

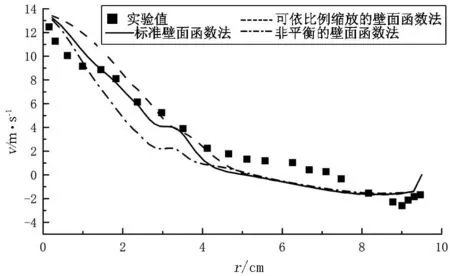
(d)z=560mm处轴向速度对比

图7不同近壁面模型的速度分布对比

5结论

(1)k-ε模型和k-w模型都是基于各向同性假设的湍流模型，雷诺应力模型(RSM)是基于各向异性假设的湍流模型.旋风分离器内部的流场是各向异性的，故只有雷诺应力模型才能准确反映出内部的流动情况.

(2)一阶迎风格式不能够反映旋风分离器内部的流动情况.利用二阶迎风格式的模拟结果更符合实验值.

(3)总体上，近壁面处理方法中非平衡的壁面函数法最能够反映旋风分离器内部流场的实际情况.

参考文献

[1] 路伟,胡少波,方敏.基于CFD的螺旋式旋风分离器数值模拟[J].湖北工业大学学报,2012,27(4):37-40.

[2] 赵通,杨亚平,刘俊龙.稳态与非稳态下旋风分离器气相流场数值模拟方法研究[J].动力工程学报,2012,32(8):591-597.

[3] Fraser S M, Abdel Razek A M, Abdullah M Z.Computation and experimental investigations in a cyclone dust separator[J]. Proc Insrn Mesh Engrs,1997,22:247-257.

[4] Hsieh K T,Rajamani R K.Mathematical model of thehydrocylone based on physics of fluid flow [J]. AIChE Journal, 1991,37(5):735-746.

[5] 龚光彩,杨周周,朱少林.轴入式旋风分离器分步湍流模型的数值模拟与试验[J].湖南大学学报,2012,39(2):19-24.

[6] 韩婕,刘阿龙,彭东辉,等.旋风分离器两相流动数值模拟研究进展[J].天然气化工,2012,37(5): 55-61.

[7] 王军,陈宁.旋流器流场模拟及特性分析[J]. 江苏科技大学学报,2012,26(4):366-369.

[8] Azadi M,Moheebbi A H. A CFD study of effect of cyclone size on its performance parameters [J] .Journal of Hazarous Materials,2010,182(60):835-841.

(编辑：郝秀清)