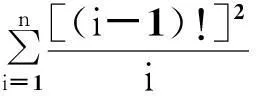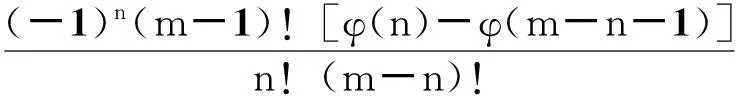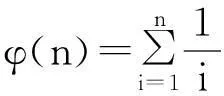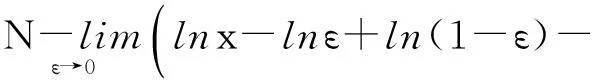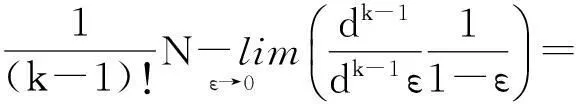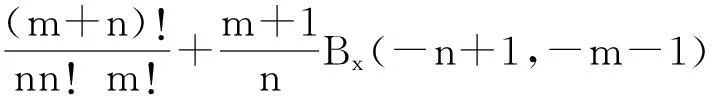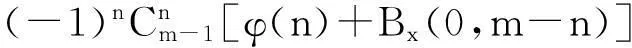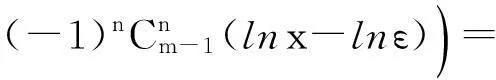关于不完全Beta函数的注记

蒋亚萍， 孙中锋， 秦惠增

(山东理工大学 理学院， 山东 淄博 255049)

关于不完全Beta函数的注记

蒋亚萍， 孙中锋， 秦惠增

(山东理工大学 理学院， 山东 淄博 255049)

摘要：Özçag E等运用Neurix极限将不完全Beta函数Bx(a,b)中a,b的取值范围扩展到了整个实数域，并给出了a,b为负整数时不完全Beta函数的显示表达式，其结果发表于Journal of Mathematical Analysis and Applications. 但是，我们认为其推导过程中存在错误，在此指出错误之处，并给出相应的更正结果.

关键词：特殊函数； 不完全Beta函数； Neurix极限； 实数域

收稿日期：2015-04-22

基金项目：国家自然科学基金项目(61379009;11226315)

通信作者：

作者简介：蒋亚萍，女，jiangyapingg@163;秦惠增，男，qinhz000@163.com

文章编号：1672-6197(2016)01-0018-03

中图分类号：O172.2

文献标志码：A

Abstract:Özçag E et al. extended the incomplete beta function Bx(a,b) to all real values of a,b by using the neutrix limit, which was published in “ Journal of Mathematical Analysis and Applications”. Specially, the authors achieved the explicit expression of Bx(a,b) for negative integer values of a or b. In this paper, we point out that there are some errors in their deduction progress and study the corresponding correction.

A note about the incomplete Beta function

JIANG Ya-ping， SUN Zhong-feng， QIN Hui-zeng

(School of Science, Shangdong University of Technology, Zibo 255049, China)

Key words: the special function; the incomplete Beta function; Neutrix limit； real values

通常，不完全Beta函数被定义为[1]

a,b>0,0

(1)

不完全Beta函数被广泛用于统计学、精算学、经济、金融、生存分析、通信等学科上,因此,Özçag E等在文献[2]中使用Neutrix calculus[3-5]扩展a,b的取值范围，使不完全Beta函数具有更广的适用范围是非常有意义的.然而,我们发现文献[2]中的部分结果是错误的.本文指出文献[2]中的错误,并给出相应的更正结果.

1问题

在文献[2]中，Özçag E等利用下面的Neutrix极限

0

(2)

将不完全Beta函数中的a,b的取值范围扩展到了整个实数域上.进一步地,利用Neutrix极限

lnmtlnn(1-t)dt,0

(3)

1)当n=1,2,…时,

(4)

见文献[2]中的式(10).

2)当n=1,2,…时，

(5)

见文献[2]中的式(13).

3)当m=n+1,n+2,…,n=1,2,…时，

Bx(-n,m)=

(6)

4)当m,n=1,2,…时，

Bx(-n,-m)=

(7)

下面我们指出出现错误结果1)～4)的原因，并给出正确的结果.

2主要结果

定理 1

Bx(0,n)=

(8)

证明根据式(2)及Neutrix极限,可以得到

(9)

定理 2

n=1,2,…

(10)

证明按照定理1的证明方法, 有

(11)

结合式(11)和下面的等式

k=1,2,…,n,

(12)

可知式(10)成立.

导致文献[2]中式(13)错误的原因是使用了下面这个错误的结果

[(k-1)!]2

(13)

应被更正为式(12).

定理 3

Bx(-n,-m)=

φ(m+n)]

(14)

式中m,n=1,2,….

证明对不完全Beta函数的定义即式(2)分部积分,可得

Bx(-n,-m)=

(15)

利用

以及Neutrix极限,就有

(16)

反复利用递推公式(16),得到

Bx(-n,-m)=

(17)

结合式(10)和式(17)得式(14).

比较式(14)和式(7)可知，式(7)是不正确的, 其原因也是在证明过程中使用了错误的结果式(13).

定理 4

Bx(-n,m)=

(18)

其中

In,m(x)=

(19)

n=1,2,….

证明按照定理3的证明方法,可得

(20)

反复利用递推公式(20),得到

Bx(-n,m)=

(21)

结合式(20)和式(21)可知式(18)成立.

比较式(6)和式(18)可知, 式(6)是不正确的.式(18)可以写成下面更简单的形式.

定理5当m=n+1,n+2,…,n=1,2,…时，下面的恒等式是成立的.

(22)

证明由二项式定理可知,

由此可得式 (22).

参考文献

[1] Gradshteyn I S,Ryzhik I M. Tables of integrals,series,and products[M]. 6th ed. San Diego:Academic Press,2000.

[3] Fisher B,Kuribayashi Y. Neutrices and the Beta function[J]. Rostock Math Kolloq,1987,32:56-66.

[4] van der Corput J G. Introduction to the Neutrix calculus[J]. J Anal Math,1959, 7(1):281-398.

[5] Jack Ng Y,van Dam H. Neutrix calculus and finite quantum field theory[J]. J Phys A,2005,38:317-323.

(编辑：郝秀清)