考虑流固耦合的隧道开挖引起地表沉降数值分析

考虑流固耦合的隧道开挖引起地表沉降数值分析

孙厚超1，2，王国良1，杨平2*

(1.盐城工学院 土木工程学院，江苏 盐城 224051；2.南京林业大学 土木工程学院，南京 210037)

摘要：基于流固耦合分析理论，利用有限元分析软件对隧道开挖引起的地表沉降进行分析。非降水开挖方式下，考虑流固耦合效应共同作用，详细分析隧道周边地层和超前预支护加固区的主要土体特性对地表沉降及隧道结构体变形的影响。研究表明：在非降水开挖时，地表沉降、隧道拱顶下沉、隧道底部位移随着渗透系数比的增大而减小。但减小的速率也随之渗透系数比的增大而减小；随着超前预支护加固区渗漏部位的渗透系数比的增大，隧道顶部区域加固引起的地表沉降最小，两侧加固、底部加固和全部区域加固引起的地表沉降接近；地下水位变化时，超前预支护加固区周边地表沉降随着下渗总流量的增大而减小，但减小的速率也随着下渗总流量的增大而减小。此结论对富水地区采用非降水开挖隧道时的地表沉降分析提供一定的理论指导，有助于改进超前预支护和隧道排水工程的施工设计。

关键词：非降水开挖；流固耦合；数值分析；渗透系数；沉降

中图分类号：S 773.3

文献标识码：A

文章编号：1001-005X(2015)03-0112-06

Abstract：Based on the coupled fluid-solid theorem，numerical analysis for the tunneling-induced land subsidence computation was done with finite element analysis.Considering fluid-structure coupling effect，the rules of influence of the main soil characteristics of surrounding strata and advanced support reinforced zones to surface subsidence of soil and the deformation of tunnel structure were analyzed in detail for the tunneling without dewatering.The results showed that the land tends to subsidence，and the displacement of tunnel decreased as the permeability coefficient increased.But the decline rate also reduced with the increase of permeability coefficient.As the permeability coefficient of strengthened leakage section increased，the land subsidence of the enhanced area of tunnel decreased.The land subsidence at the lateral enhanced area，bottom enhanced area，and all enhanced area were almost the same.When the ground water level changed the land settlement of enhanced area decreased as the leaking amount increased.But the decreasing rate reduced as the leaking amount increased.The research results can provide certain theoretical guidance for tunneling without dewatering in water abundant area，which is helpful for improving the design and construction level of advanced support and tunnel drainage.

Keywords：tunneling without dewatering；coupled fluid-solid；numerical analysis；permeability coefficient；settlement

收稿日期：2014-12-18

基金项目：住房与城乡建设部科技开发项目(2014-K4-024)

作者简介：第一孙厚超，博士, 高级工程师。研究方向：岩土与地下工程。

通讯作者：`*杨平，博士，教授，研究方向：岩土与地下工程。E-mail:yangping@njfu.edu.cn

Numerical Analysis of Tunneling-Induced GroundSettlement with Consideration of Fluid-Solid Coupling

Sun Houchao1，2，Wang Guoliang1，Yang Ping2*

(1.College of Civil Engineering，Yancheng Institute of Technology，Yancheng 224051，Jiangsu Province；

2.College of Civil Engineering，Nanning Forestry University，Nanjing 210037)

引文格式：孙厚超，王国良，杨平，等.考虑流固耦合的隧道开挖引起地表沉降数值分析[J].森林工程，2015，31(3)：112-116.

城市的地质条件复杂，多以土体为主，常有膨胀土、沙层、高地下水位。而且城市地下工程埋深浅，周边建筑、道路、市政管线多，开挖造成的影响大。因此，为保证邻近建筑设施的安全性，研究地下洞室施工开挖对地表沉降的影响是十分必要的。近年来，考虑渗流特征与开挖应力状态之间的相互作用的流固耦合计算理论得到了广泛应用。I.M.Lee[1]、Kim H.G.[2]及DaWei[3]等人研究了浅埋隧道和水下圆形断面隧道开挖过程中渗流场分布以及渗流力计算的问题。国内的孙亚峰、李地元、冉启全及平杨等[4~12]对流固耦合作用机制和实际工程应用方面也做了很多有益的探讨。但是鲜有文献涉及隧道开挖引起的地表沉降的参数分析方面的研究成果，因此，分析研究非降水开挖中隧道开挖对地表沉降的影响规律也是十分必要的。

1隧道流固耦合计算理论

1.1　土体流固耦合的控制方程 [4-6]

假设土体中土体骨架不可压缩，只能发生微小变形，孔隙水的流动服从Darcy定律、压缩服从Hook定律，非饱和土采用Bishop提出的有效应力原理。基于假设，土体流固耦合的控制方程如下。

(1)土体平衡方程。考虑到弹塑性力学的非线性问题，土体平衡微分方程宜用如下形式的增量形式：

(1)

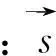
(2)有效应力原理。假定有效应力原理也适用于非饱和土，根据Bishop在1959年提出的公式，有：

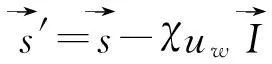
(2)

(3)渗流基本方程。渗流基本方程采用Darcy流的基本微分方程形式来表达：

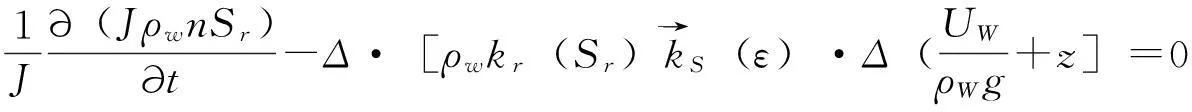
(3)

(4)土体骨架的本构方程。土体骨架的本构方程采用增量形式来表达：

(4)

(5)土体骨架变形的几何方程。只考虑小变形，则土体骨架变形采用增量形式的几何方程来表达：

(5)

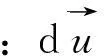
(6)吸力状态方程。假定空隙气压处处等于大气压，则土水特征曲线方程，即吸力状态方程可以采用如下形式来表达：

uw=W(Sr,n)。

(6)

式中：Sr为饱和度；n为与土体进气有关的吸力值。

1.2　土体流固耦合的基本方程

将几何方程公式(5)代入本构方程公式(4)中，经过简单运算，容易得到用土体有效应力与位移之间的关系：

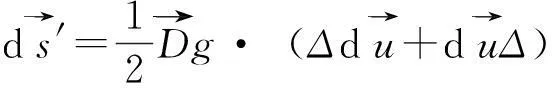
(7)

将(7)式代入公式(1)，并结合公式(2)，则得到用位移表达的土体平衡方程：

(8)

将公式(5)进行一系列变换最终可写为：

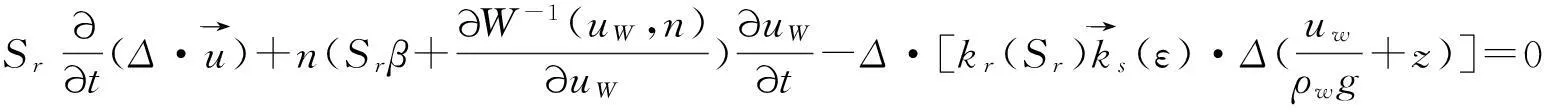
(9)

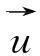
1.3　耦合效应的模拟 [7-8]

隧道开挖时地下水上涌使得周边土层的渗透系数减小，考虑到本文研究非排水开挖隧道的施工方式，渗透系数和空隙比之间的关系表达式采用如下形式：

k=k0(e/e0)e。

(10)

式中：k为对应孔隙比e的渗透系数；k0为对应孔隙比e0的渗透系数。

2开挖引起地表沉降的数值分析

2.1　计算工况

算例中计算深度取45 m，计算宽度取100 m，计算模型如图1所示。计算模型的位移边界条件为：DC边的水平及竖向位移为零，即限制其水平及竖向位移；AD，BC两边的水平位移为零，即限制其水平向位移。ABFE区域内的初始孔压为零，其中AB为地面线、FE为地下水位线。拟开挖的隧道为H=6.5 m、B=6.2 m的马蹄形断面，顶部距地面h=9.0 m。该隧道拟采用无降水开挖的施工方式，开挖轮廓线外围施作超前预支护加固区。

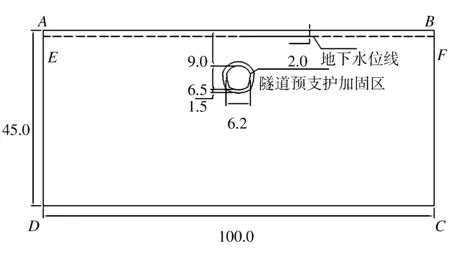
图1　非降水开挖方式下隧道施工计算模型示意图(m) Fig.1 Diagram of calculation model of tunnel construction without dewatering(Unit：m)

在有限元计算中假定地下水流动规律满足Darcy定律，土体骨架采用Drucker-Prager弹塑性本构模型，土体材料采用平面四边形四结点耦合单元来模拟。超前预支护的计算采用提高土体相关物理力学参数的等效模拟方法，等效加固区厚度取为1.5 m。

计算中涉及到的物理力学参数见表1。隧道开挖方法如图2所示，按Ⅰ→Ⅱ→Ⅲ→Ⅳ的顺序进行。

图2　非降水开挖方式下隧道开挖工法示意图 Fig.2 Diagram of tunnel construction method without dewatering(Unit：m)

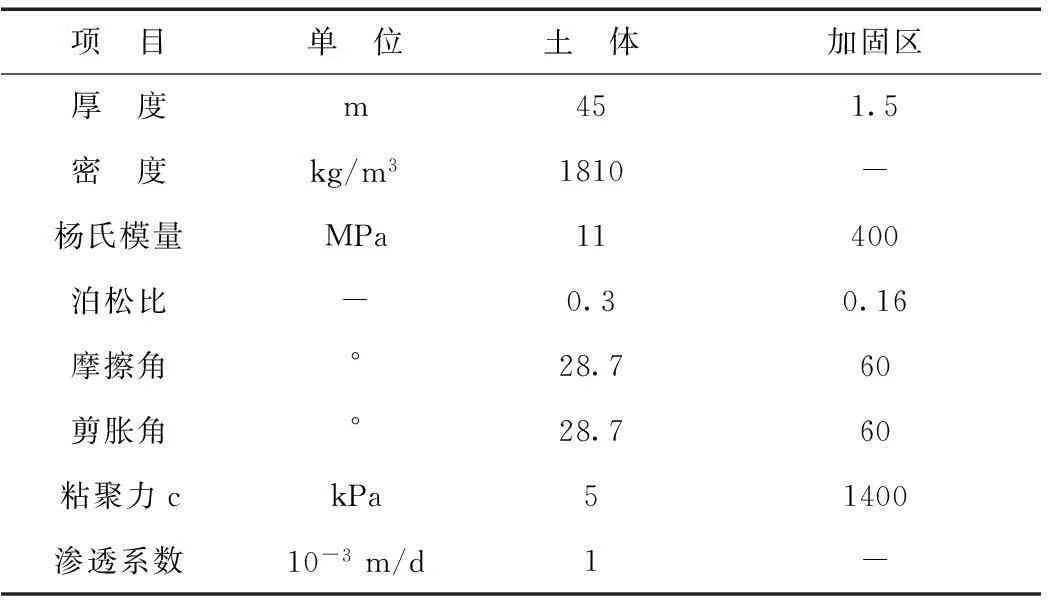
表1　非降水开挖方式下材料物理力学特性表 Tab.1 Material physical and mechanical parameter of tunnel excavation method with dewatering

2.2　加固区渗透系数对地表沉降的影响

超前预支护加固区防渗效果取决于加固区的平均渗透系数[13-14]。假定预支护加固区周边土层的渗透系数k与预支护加固区的平均渗透系数Kc的比值分别为1.0~20.0共20个数值，其中1.0表示加固体完全透水，从而得到加固区平均渗透系数对地表沉降的影响规律。

地表最大沉降与渗透系数比k/Kc关系曲线如图3所示。从图3可以看出，地表沉降最大值随着渗透系数比k/Kc的增大而减小。当k/Kc较小时，地表沉降最大值随k/Kc的增大而迅速减小，但是当k/Kc较大时，地表沉降最大值随k/Kc的增大而缓慢减小。当渗透系数比k/Kc达到10时即可认为超前预支护加固区的平均渗透系数变化对地表沉降无显著影响。

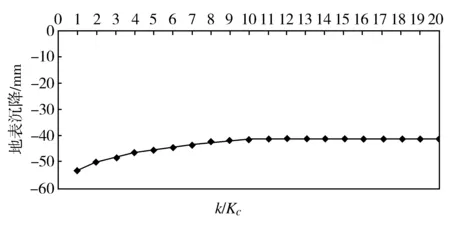
图3　地表最大沉降与渗透系数比k/K c关系曲线 Fig.3 Curve of relationship between maximum ground settlement and the permeability coefficient ratio

隧道拱顶下沉与渗透系数比k/Kc关系曲线如图4所示。从图5中可以看出，渗透系数比k/Kc对隧道拱顶下沉的影响规律与渗透系数比k/Kc对地表沉降最大值的影响规律基本相似，这里不再详述。隧道底部位移与渗透系数比k/Kc关系曲线如图5所示。从图5中可以看出，渗透系数比k/Kc对隧道底部位移的影响规律与渗透系数比k/Kc对地表沉降最大值的影响规律基本相似，这里不再详述。

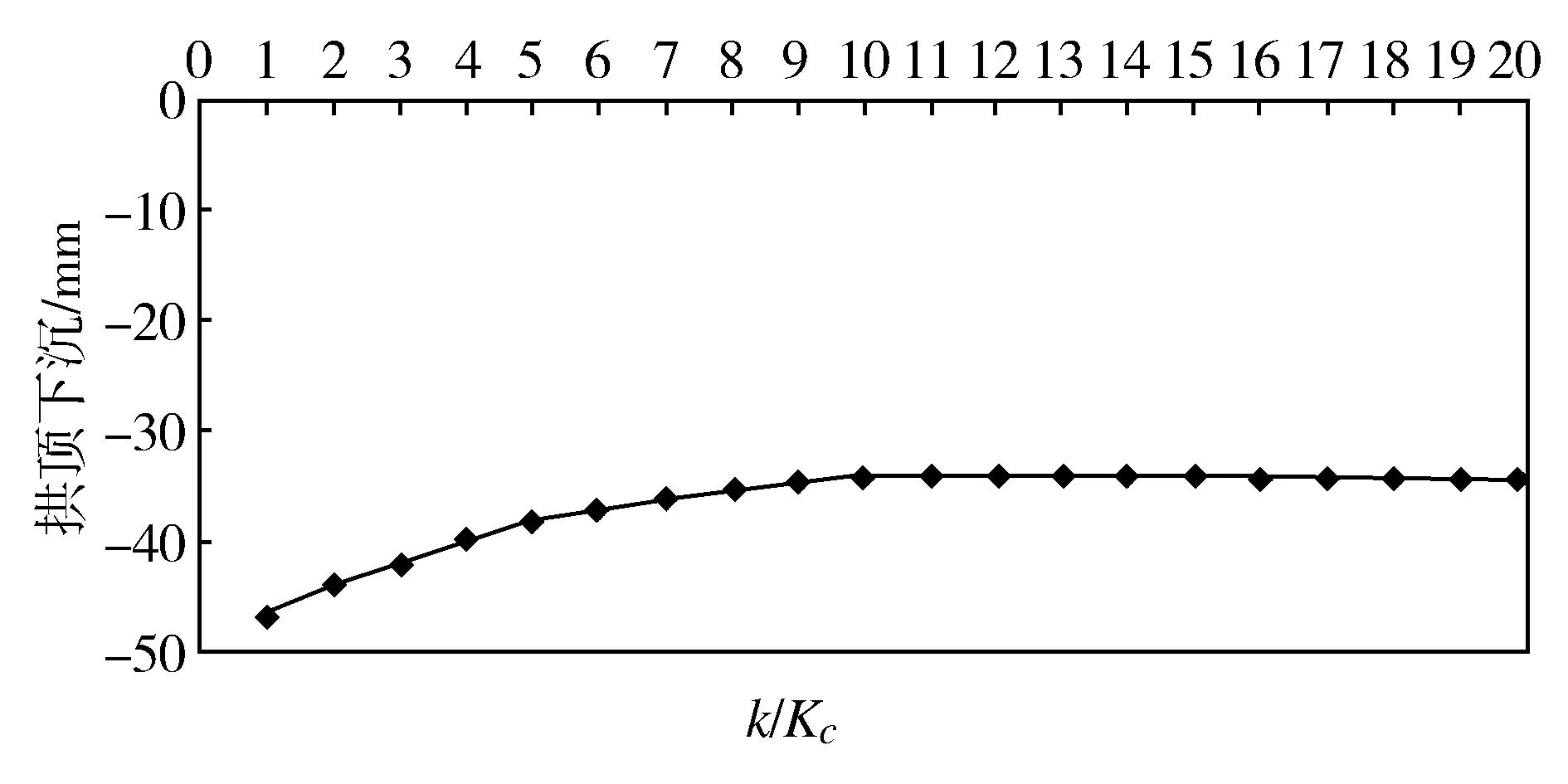
图4　隧道拱顶下沉与渗透系数比k/K c关系曲线 Fig.4 Curve of relationship between maximum tunnel vault settlement and the permeability coefficient ratio

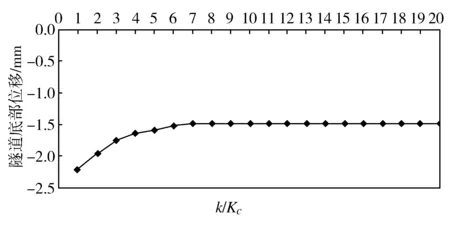
图5　隧道底部位移与渗透系数比k/K c关系曲线 Fig.5 Curve of relationship between maximum tunnel bottom settlement and the permeability coefficient ratio

2.3　加固区局部区域渗漏对地表沉降的影响

超前预支护加固区的施工质量得不到保证时，可能会导致部分区域渗漏。

假定开挖过程中出现4种不同部位的渗漏，位置示意如图6所示。示意图中加固区发生渗漏的示意部位1~4分别对应：上部、两侧、底部、全部加固区。

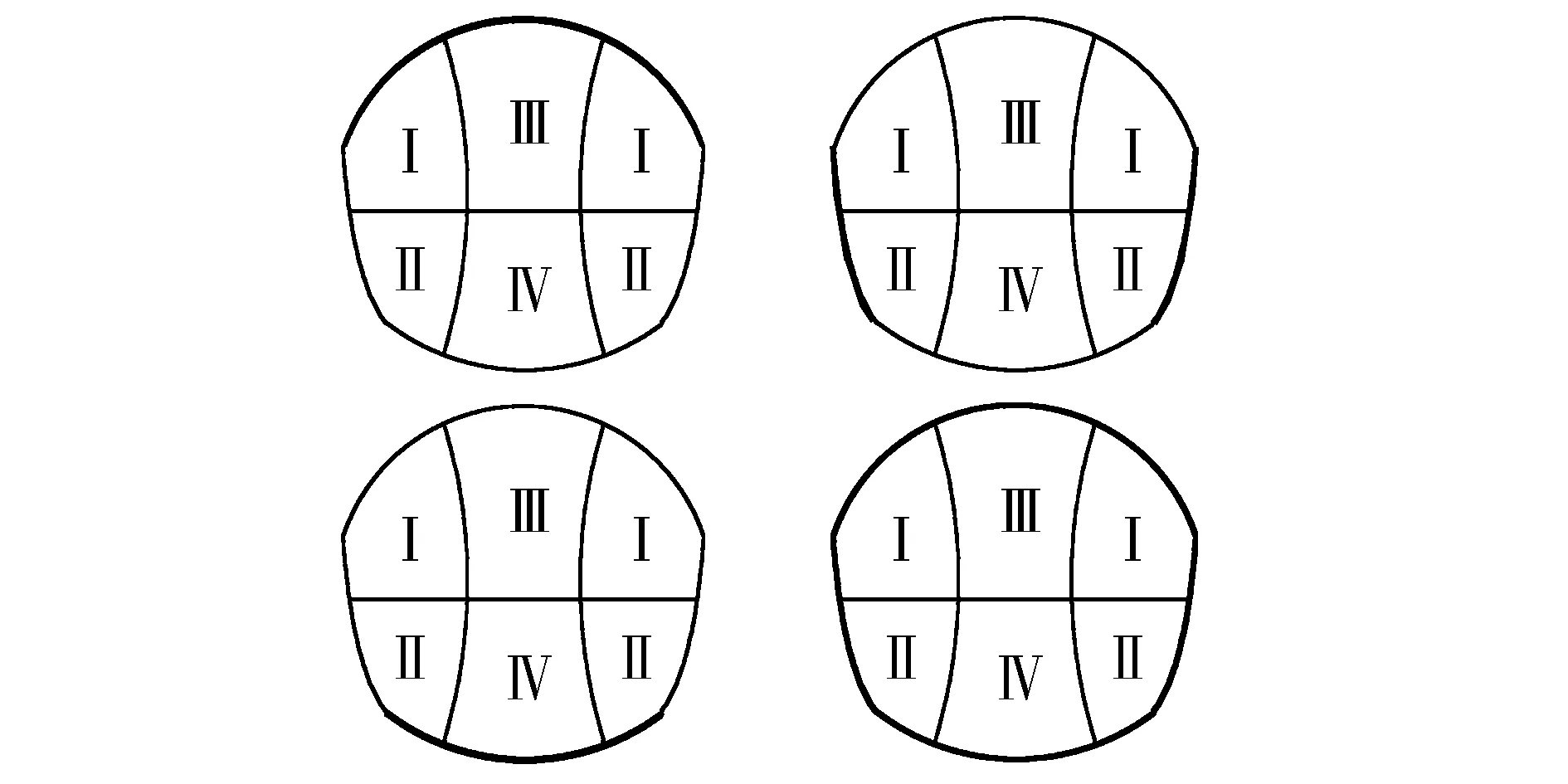
图6　隧道加固区渗漏部位示意图(粗线表示渗漏部位) Fig.6 Diagram of tunnel leakage position (thick line for reinforced zone)

假定超前预支护非渗漏加固区不透水，周边土层渗透系数k与加固区非渗漏部位平均渗透系数Kc的比值为30，其余参数同前。此外，假定超前预支护加固区周边土层渗透系数k与加固区渗漏部位平均渗透系数Kc的比值分别为1.0~20.0共20个数值，其中1.0表示加固区渗漏部位完全透水，从而得到超前预支护加固区不同部位渗漏时其平均渗透系数对地表沉降的影响规律。

超前预支护加固区不同部位渗漏时地表最大下沉与其平均渗透系数比k/Kc关系曲线如图7所示。从图7中可以看出，随着平均渗透系数比k/Kc的增大，部位2或者部位3渗漏时，地表沉降最大值最终和在部位4渗漏时的地表沉降最大值非常接近。显而易见，部位1渗漏时引起的地表沉降最小，要比其它部位渗漏时引起的地表沉降最大值小很多。

图7　不同渗漏部位的地表最大沉降与渗透系数比k/K c关系曲线 Fig.7 Curve of relationship between maximum ground settlement of different leakage position and the permeability coefficient ratio

2.4　地下水位变化对地表沉降的影响

参考2.1中的算例，超前预支护加固区的平均渗透系数取为1.0×10-4m/d。模型计算时，假设施工过程的在21~30 d，整个地表区域的下渗总流量分别取0.1~0.6 m3/d共6个数值，从而可以分析得到地下水位变化对地表沉降的影响规律。

周边地表沉降与地下水位变化关系曲线如图8所示。从图8中可以看出，周边地表沉降随着整个区域的下渗总流量的增大而减小，但减小的速率也随着下渗总流量的增大而减小。无下渗流量时，地表沉降最大。

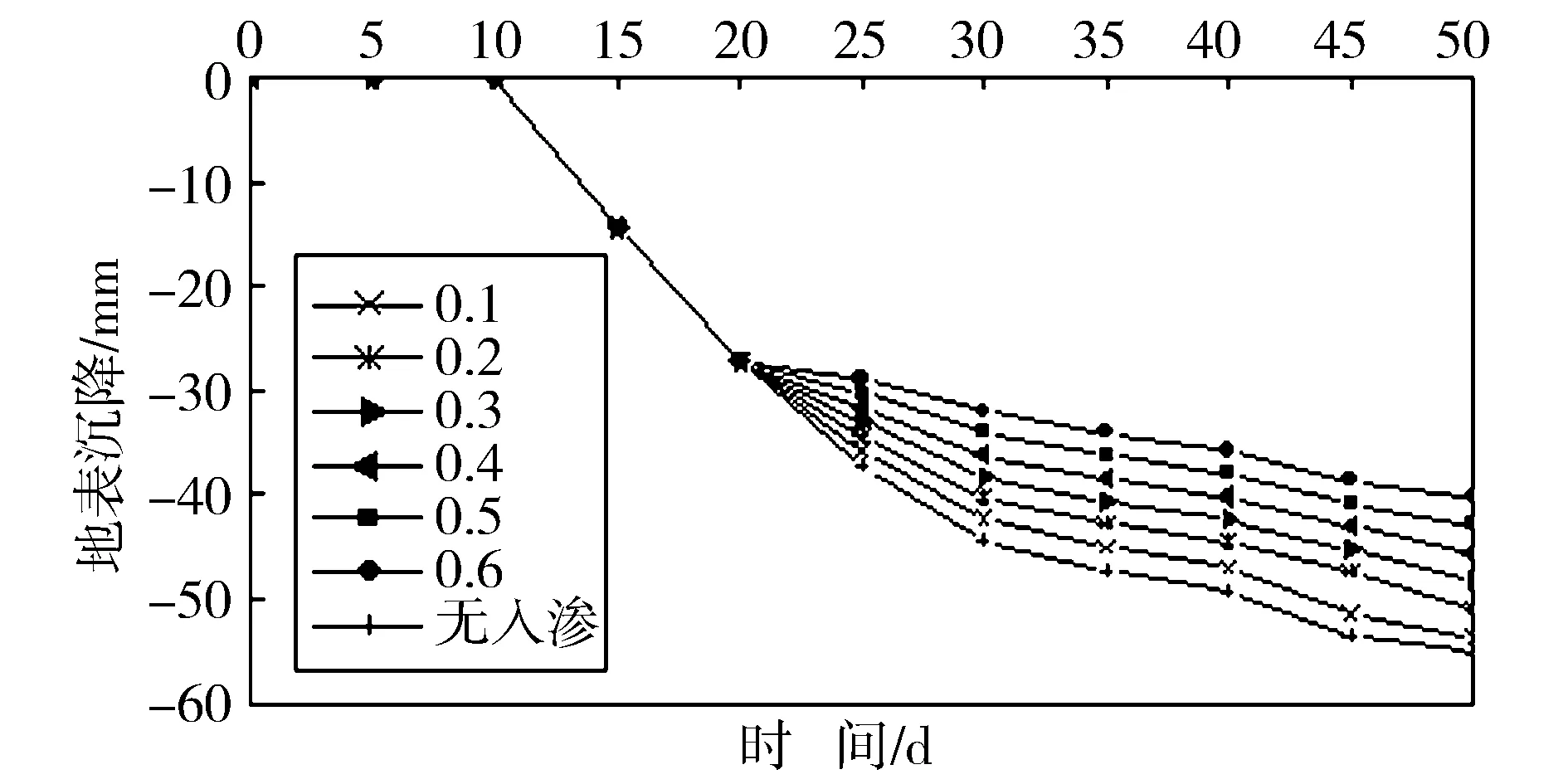
图8　周边地表沉降与地下水位变化关系曲线 Fig.8 Curve of relationship between maximum ground settlement and the change of ground water level

隧道拱顶下沉与地下水位变化关系曲线如图9所示。从图9中可以看出，地下水位变化对隧道拱顶下沉的影响很小。

图9　隧道拱顶下沉与地下水位变化关系曲线 Fig.9 Curve of relationship between maximum tunnel vault settlement and the change of ground water level

隧道底部位移与地下水位变化关系曲线如图10所示。从图10中可以看出，地下水位变化对隧道底部位移的影响很小。

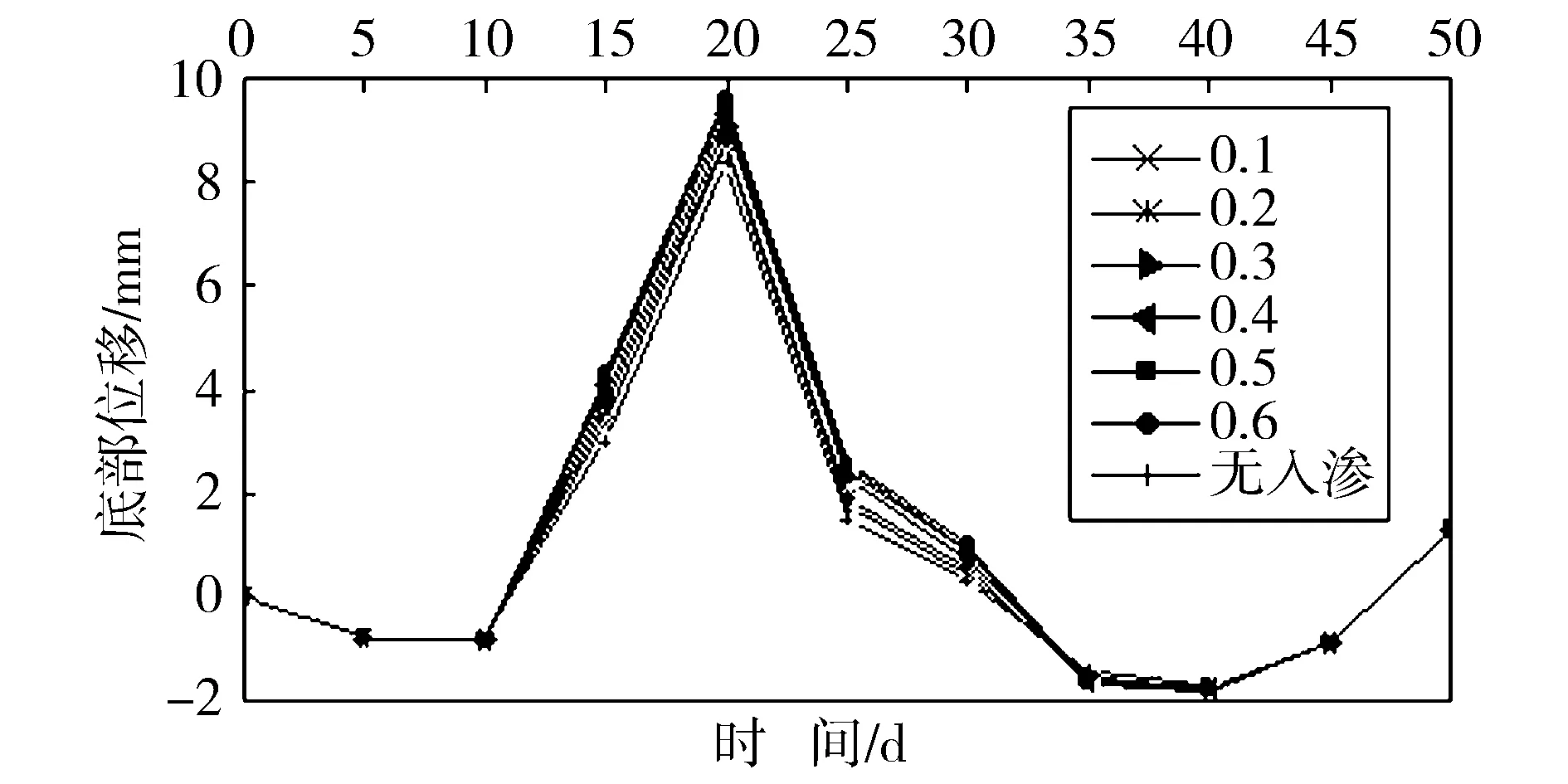
图10　隧道底部位移与地下水位变化关系曲线 Fig.10 Curve of relationship between maximum tunnel bottom settlement and the change of ground water level

3结论

基于土体流固耦合理论，通过有限元分析，研究了采用非降水开挖方式施工时隧道周边土层和超前预支护加固区的主要土体特性对地表沉降、隧道拱顶下沉、底部位移的影响规律。主要土体特性是指隧道的超前预支护加固区渗透系数、局部渗漏、地下水位变化等因素。

(1)在非降水开挖时，超前预支护加固区周边土层的渗透系数与加固区平均渗透系数之比值称为渗透系数比。地表沉降、隧道拱顶下沉、隧道底部位移随着渗透系数比的增大而减小。但减小的速率也随之渗透系数比的增大而减小，到某一比值时即可认为加固区的渗透系数不再对地表沉降、隧道拱顶下沉、隧道底部位移产生明显影响。

(2)随着超前预支护加固区渗漏部位的渗透系数比的增大，隧道顶部区域加固引起的地表沉降最小，两侧加固、底部加固和全部区域加固引起的地表沉降接近。

(3)地下水位变化时，超前预支护加固区周边地表沉降随着下渗总流量的增大而减小，但减小的速率也随着下渗总流量的增大而减小。当没有下渗流量时，地表沉降最大。但是，地下水位变化对隧道拱

顶下沉、隧道底部位移的影响很小，可忽略不计。

【参考文献】

[1]Lee I M，Nam S W.The study of seepage forces acting on the tunnel lining and tunnel face in shallow tunnels [J].Tunnels and Underground Space Technology，2001，16(1)：31-40.

[2]Kim，H G.A new coupling strategy for fluid-solid interaction problems by using the interface element method[J].International Journal for Numerical Methods in Engineering，2010，81(4)：403-428.

[3]Mao D，Nilsen B，Lu M，et al.Numerical analysis of rock fall at Hanekleiv road tunnel [J].Bulletin of Engineering Geology and the Environment，2012，71(4)：783-790.

[4]孙亚峰.软流塑地层地铁区间隧道施工效应有限元分析[J].国防交通工程与技术，2004(3)：32-35.

[5]李地元，李夕兵，张伟，等.基于流固耦合理论的连拱隧道围岩稳定性分析[J].岩石力学与工程学报，2007，26(5)：1056-1063.

[6]冉启全，顾小芸.考虑流变特性的流固耦合地面沉降计算模型[J].中国地质灾害与防治学报，1998，9(2)：99～-103.

[7]余学彦.考虑流固耦合的城市隧道施工稳定性及地表沉降分析[D].南京：河海大学，2006.

[8]董倩，孔凡林，赵宝云.城市隧道穿越填方地带数值模拟及沉降控制研究[J].公路工程，2013，04：44-49.

[9]熊慧中，王平，吕鑫，等.超浅埋大跨度连拱隧道下穿国道沉降控制研究[J].公路工程，2014，06：25-28+55.

[10]平扬，白世伟.深基坑工程渗流—应力耦合分析数值模拟研究[J].岩土力学，2001，22(1)：37-41.

[11]黎水泉，徐秉业.双重孔隙介质流固耦合理论模型[J].水动力学研究与进展，2001，16(4)：460-466.

[12]吉小明，白世伟.与应变状态有关的岩体双重孔隙介质流固耦合的有限元计算[J].岩石力学与工程学报，2003，22(10)：1636-1639.

[13]赵阳升，王瑞凤.高温岩体地热开发的块裂介质固流热耦合三维数值模拟[J].岩石力学与工程学报，2002，21(12)：1751-1755.

[14]陈祖安，伍向阳.砂岩渗透率随静压力变化的关系研究[J].岩石力学与工程学报，1995，14(2)：155-159.

[责任编辑：董希斌]