主动控制和状态反馈控制相结合的超混沌系统同步

郑小帆, 颜闽秀

(沈阳化工大学 信息工程学院， 辽宁 沈阳 110142)

在混沌同步控制中，控制器参数的给定主要依靠设计者的经验或者是对系统的充分认识.近年来，线性矩阵不等式(LMI)方法[11]，由于其具有高效的求解算法和能获得全局最优解的特点，引起了控制界的关注，成为鲁棒控制分析与设计的重要方法.但该方法求取的结果相对保守，且可解性较低.因此，本文针对超混沌系统的同步问题设计了主动静态输出状态反馈控制器.反馈的增益矩阵采用一种相对于LMI方法具有较好可解性的迭代线性矩阵不等式(ILMI)算法来获取.最后，通过仿真验证了该控制器的有效性.

1 同步误差系统的描述

将非线性超混沌系统作为主动系统：

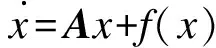
y(t)=Cx(t)

(1)

将另一个超混沌系统表示为被动系统：

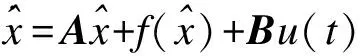
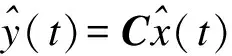
(2)

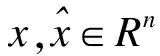
将系统(1)和(2)的同步误差表示为：

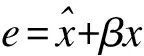
(3)

当β=[-1,-1,…,-1,-1]T时，表示两个系统完全同步，当β=[1,1,…,1,1]T时，表示两个系统是反同步.

同步和反同步误差的微分方程可以描述为：

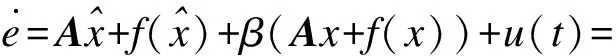
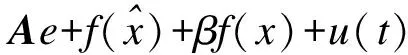
(4)

通过设计加在响应系统上的控制器，使得驱动系统和响应系统达到同步，即要满足

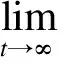
2 控制器的设计和分析

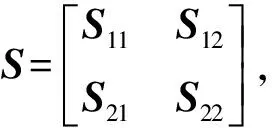
(1)S<0.

推论1对于给定的X>0,如果存在正定的对称矩阵PT=P和相应的K满足下列的线性矩阵不等式：

(5)

动力学系统(4)是稳定的，控制器形式为

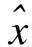
(6)

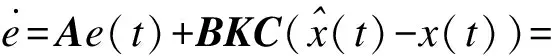
(A+BKC)e(t)

(7)

选取正定的李雅普诺夫函数为V=eT(t)Pe(t)>0,其中PT=P>0.

把该函数对时间进行求导得

eT(t)[(A+BKC)TP+P(A+BKC)]e(t)≤

eT(t)[(A+BKC)TP+P(A+BKC)+

CTKTKC]e(t)=eT(t)[ATP+PA-PBBTP+

(BTP+KC)T(BTP+KC)]e(t)

(8)

显然-PBBTP≤0，即-PBBTP是非正定的.该不等式不能简化成线性矩阵不等式的形式.因此，引入了一个附加的正定的对称矩阵变量X.显然(X-P)TBBT(X-P)≥0,其中X和P具有相同的维数.那么可有

-XBBTP-PBBTX+XBBTX≥-PBBTP

(9)

公式(8)可以化简为：

PBBTX+XiBBTX+

(BTP+KC)T(BTP+KC)]e(t)

(10)

如果下列的矩阵不等式成立

ATP+PA-XBBTP-PBBTX+XBBTX+

(BTP+KC)T(BTP+KC)≤0

(11)

可得

(12)

基于李雅普诺夫理论，如果存在一个正定的对称矩阵PT=P和相应的矩阵K满足矩阵不等式(11)成立，则系统(4)是稳定的，即两个超混沌系统能够稳定同步.

应用定理1，选取S22=-I，矩阵不等式(11)可以等价为

(13)

如果给定一个正定的对称矩阵X，公式(13)就可以简化为求解未知P和K的LMI问题.

证明完毕.

定理2当且仅当存在P和K满足下列矩阵不等式(14)时，动力学系统(4)是α稳定的.

ATP+PA-XBBTP-PBBTX+XBBTX+

(BTP+KC)T(BTP+KC)-αP≤0

(14)

此时，在整个复频域中，闭环系统矩阵的特征值都在R(s)=α的左边平面.随着α的减小，闭环系统的特征值也在R(s)=α的左半平面内平移.当α<0时，闭环系统矩阵的特征值都在负半平面，系统就达到稳定了.为了增加LMI有解的可能性，引入了迭代线性矩阵不等式(ILMI)算法对不等式(13)进行求解.设系统由(A,B,C)表示，迭代线性矩阵不等式算法的步骤如下：

步骤1： 选取Q>0，根据黎卡提方程ATP+PA-PBBTP+Q=0,P=PT>0求解得到P.设j=1，X1=P.

步骤2： 求解下列关于Pj、K和αj的最优化问题.

OP1.求解以下约束条件下αj的最小值.

(15)

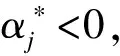
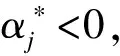
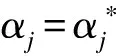
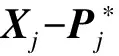
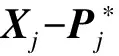
步骤7： 如果ILMI算法不能得到合适的增益矩阵，应重新选定矩阵Q，再次进行ILMI算法.

3 仿真分析与讨论

为了便于数值仿真,假设式(4)中的参数：

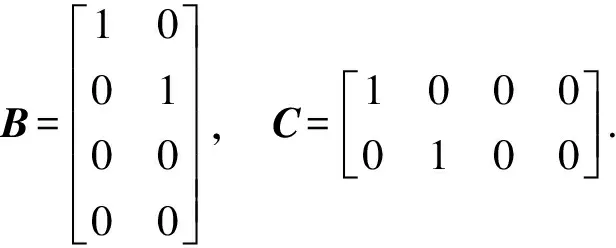
(16)

为了验证所设计的修正投影同步控制器的有效性，以超混沌Lorenz 系统和Chen 系统为例进行研究.超混沌Chen系统可以用下面的方程表示：

(17)

其中a=35,b=7,c=12,d=3,r=0.5.

超混沌Lorenz系统可以用下面的方程表示：

(18)

其中a=10,b=28,c=8/3,d=1.3.

3.1 超混沌Chen系统的同步

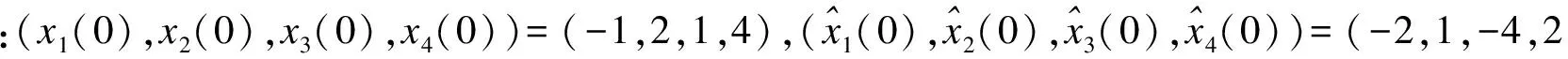
选取X=I，使用Matlab中的LMI工具箱直接求解推论1中的线性矩阵不等式，然而却得不到一个可行的结果.选取Q=I，利用迭代LMI算法来求解相应的LMI问题，得到了一系列可行的结果.推论1的仿真结果和应用迭代LMI算法的结果的可行性见表1.由迭代LMI算法计算得到的P如下所示：

(19)

表1 LMI和ILMI算法的求解结果

Table 1 Solve results of LMI and ILMI algorithm

通过数值仿真结果可以看出：两个系统的同步误差在10 s前没加入控制时不为0，在第10 s加入控制器后很快达到稳定并且误差是趋于零的.即加入设计的输出状态反馈控制器后，两个超混沌系统能达到很好的同步效果.系统的同步误差如图1所示.

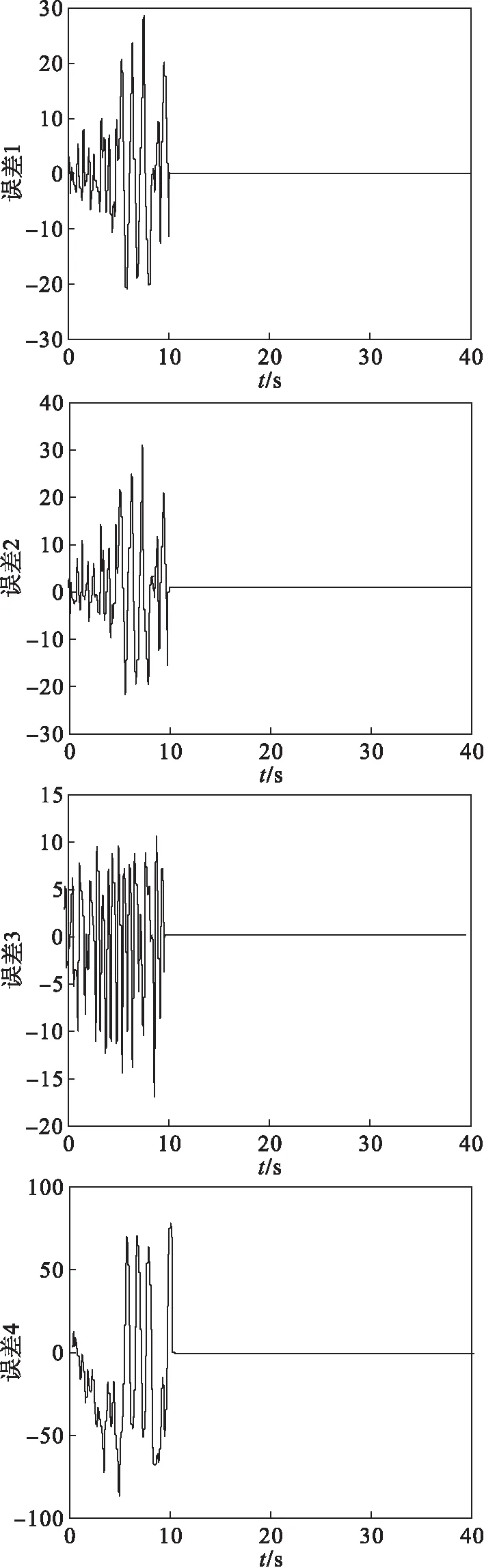
图1 Chen系统的同步误差

3.2 超混沌Lorenz系统的反同步

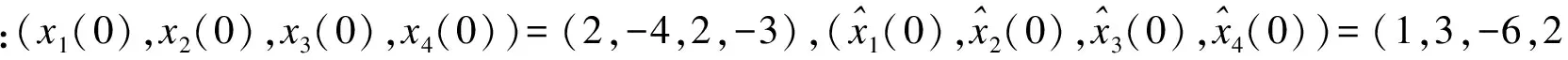
选取X=I,推论1的直接仿真结果和应用迭代LMI算法结果的可行性见表2.选取Q=I，由迭代LMI算法计算得到的P如下：

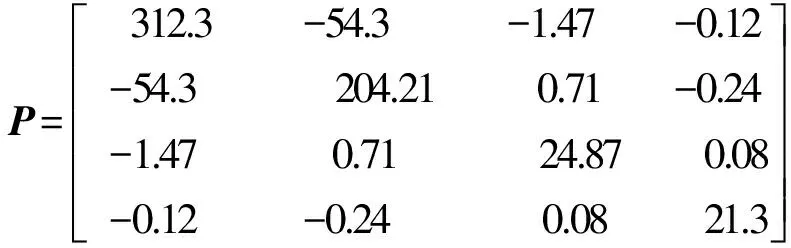
(20)

表2 LMI和ILMI算法的求解结果

Table 2 Solve results of LMI and ILMI algorithm

系统的同步误差如图2所示.由图2可以看出：两个系统的同步误差在10 s前没加入控制时不为0，在第10 s加入控制器后很快达到稳定并且误差趋于0,即加入设计的输出状态反馈控制器后，两个超混沌系统能达到很好的反同步效果.

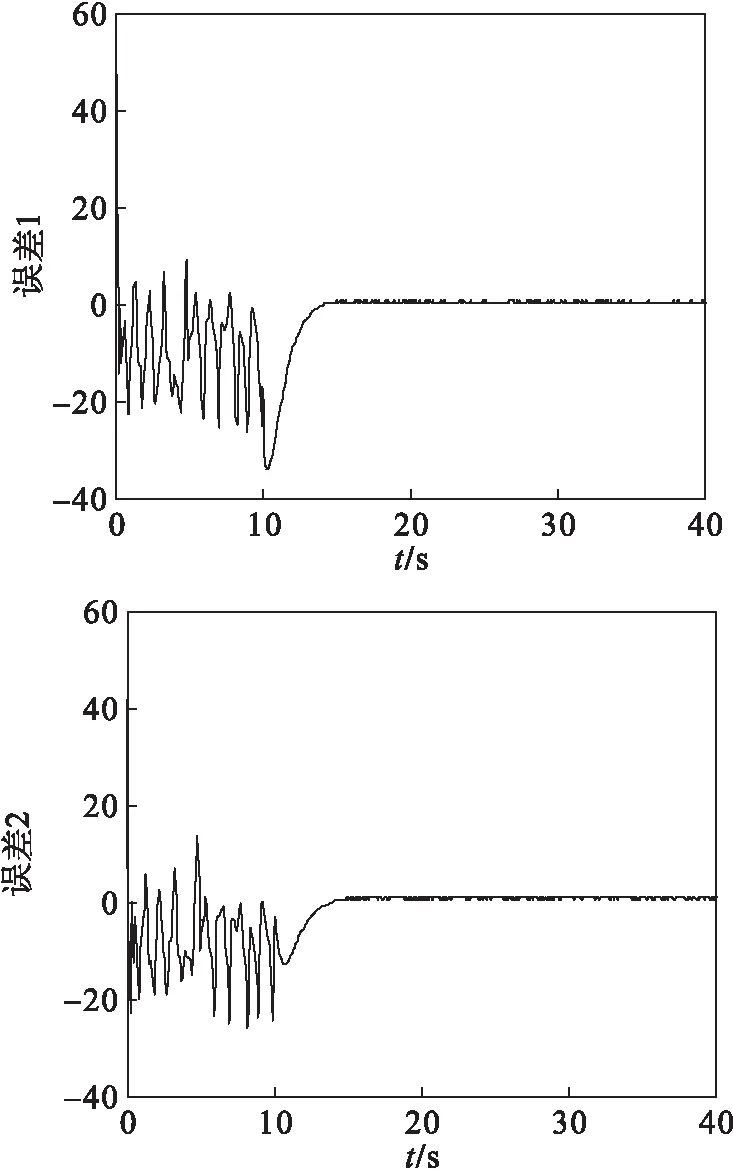
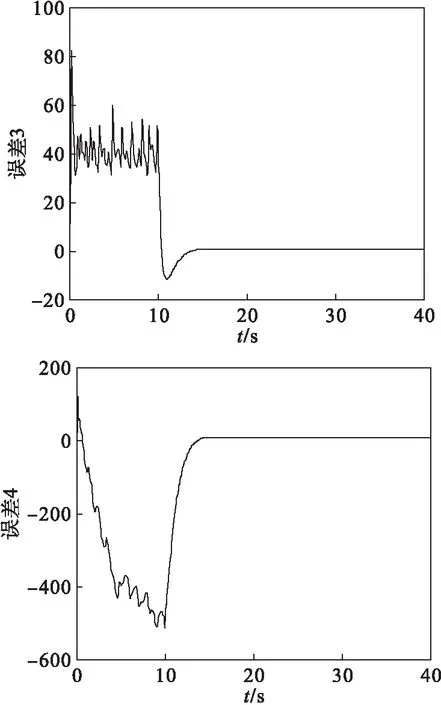
图2 Lorenz系统的反同步误差

4 结 论

研究了超混沌系统的同步问题.利用Lyapunov稳定理论，给出了主动静态输出反馈控制器的设计方法及求解反馈增益矩阵的线性矩阵不等式，并将这种混沌系统同步方法应用于超混沌Chen系统的同步和Lorenz系统的反同步中.实验表明：迭代线性矩阵不等式(ILMI)算法比LMI方法更容易得到可行解.数值仿真验证了所设计控制器的有效性.

[1] PECORA L M,CARROLL T L.Synchronization in

Chaotic Systems[J].Physical Review Letters,1990,64(8):821-824.

[2] 谭文,蒋逢灵,王耀南，等.一类混沌系统的滑动模态同步控制及其应用[J].计算机工程与应用,2013,49(7):232-234.

[3] 高远,罗文产,戴喜生，等.不确定性超混沌系统的积分滑模同步控制研究[J].自动化仪表,2012,33(5):15-17.

[4] LI W L,CHANG K M.Robust Synchronization of Drive-response Chaotic Systems via Adaptive Sliding Mode Control[J].Chaos,Solitons & Fractals,2009,39(5):2086-2092.

[5] LI X F,LEUNG A C S,HAN X P，et al.Complete(Anti-) Synchronization of Chaotic Systems with Fully Uncertain Parameters by Adaptive Control[J].Nonlinear Dynamics,2011,63(1):263-275

[6] HO M C,HUNG Y C,CHOU C H.Phase and Anti-phase Synchronization of Two Chaotic Systems by Using Active Control[J].Physics Letters A,2002,296(1):43-48.

[7] YASSEN M T.Chaos Synchronization between Two Different Chaotic Systems Using Active Control[J].Chaos,Solitons & Fractals,2005,23(1):131-140.

[8] AHN C K.T-S FuzzyH∞Synchronization for Chaotic Systems via Delayed Output Feedback Control[J].Nonlinear Dynamics,2010,59(4):535-543.

[9] YANG X,CAO J,LU J.Stochastic Synchronization of Complex Networks with Nonidentical Nodes via Hybrid Adaptive and Impulsive Control[J].IEEE Transactions on Circuits and Systems I:Regular Papers,2012,59(2):371-384.

[10] 姚利娜,高金峰,廖旎焕.实现混沌系统同步的非线性状态观测器方法[J].物理学报，2006,55(1):35-41.

[11] BOYD S,GHAOUI L,Feron E.Linear Matrix Inequalities in System and Control Theory[J].Proceedings of the IEEE,1997,85(4):698-699.