限制位移桥墩的连续刚构桥抗震性能研究
限制位移桥墩的连续刚构桥抗震性能研究
刘鹏1,2
(1.中国中铁二院工程集团有限责任公司,四川 成都610031; 2.西南交通大学 土木工程学院,四川 成都610031)
摘要:沿着摇摆桥墩的概念提出一种限制位移桥墩连续刚构桥体系。该体系通过对连续刚构桥墩底和承台之间采取一定措施,使桥梁在地震发生时能够在限制的位移量内活动,减小输入到桥梁结构中的能量,达到减震的目的。通过对一座铁路连续刚构桥的分析,发现这种限制位移桥墩连续刚构桥体系能大幅减小桥墩的延性和强度地震需求,减震效果明显,在选择合适的限制位移量的情况下,可保证桥墩在高烈度罕遇地震作用下几乎保持弹性工作状态,震后经简单处理即可保证使用功能,为震后救援工作带来极大便利,也大大减少了修复成本。
关键词:地震; 连续刚构桥; 限制位移; 桥墩
收稿日期:*2014-04-29
基金项目:中国中铁二院工程集团有限公司院级课题(13164190(13-15),14126165(14-15))
作者简介:刘鹏(1982-),男,博士,高级工程师,主要从事桥梁抗震研究.E-mail:bridge.liupeng@qq.com
中图分类号:U442.55文献标志码:A
DOI:10.3969/j.issn.1000-0844.2015.01.0120
Seismic Performance of a Continuous Rigid Frame Bridge
with Displacement-restricted Piers
LIU Peng1,2
(1.ChinaRailwayEryuanEngineeringGroupCo.Ltd,Chengdu,Sichuan610031,China;
2.SchoolofCivilEngineering,SouthwestJiaotongUniversity,Chengdu,Sichuan610031,China)
Abstract:Since the beginning of the 1990s,performance-based seismic design theory has entered the mainstream of structural seismic research.The purpose of performance-based seismic design theory is to determine the seismic performance objectives of a building based on its use,importance,and level of seismic fortification.Buildings designed in accordance with those objectives will safely withstand earthquakes that may occur in the future.On the bridge,plastic hinges placed on the piers were used to consume earthquake energy.Design for ductility can avoid collapse of the bridge.However,permanent deformation of the plastic hinges could cause serious damage to the pier.It is difficult to immediately repair bridges following earthquakes.Many transportation functions are significantly slowed or lost.In order to ensure that the transportation capacity of bridges is recovered quickly after a strong earthquake,many structural systems have been proposed,including rocking bridge piers and self-centering bridge piers.The continuous rigid frame bridge system with displacement-restricted piers was consistent with the concept of rocking piers.This structure can realize three important functions:(1) limit the maximum displacement of pier,(2) prevent the bridge from overturning,and (3)adjust the coefficient of friction at the pier bottom.By adhering to these objectives between the pier bottom and the pier cap,the displacement-restricted system allowed the bridge to move with under the action of the earthquake.In so doing,this method can reduce the input of energy to the bridge structure and achieve the purpose of earthquake mitigation.
This study concluded that the continuous rigid frame bridge system with displacement-restricted piers could reduce ductility and strength demands on the bridge piers.This paper comparedthe displacement limits of 2 cm,5 cm,8 cm and traditional piers.The results showed that the displacement of the pier top,the bending moment at the pier bottom,and the bending moment of the pier at the bridge beam with the displacement-restricted 2 cm,5 cm,8 cm piers were much less than the piers of a traditional continuous rigid frame bridge.The results also show that the amount of displacement restrictions is important.Choosing the appropriate displacement restriction can ensure that the elastic working state of the bridge will be maintained under severe earthquake conditions.This can improve the effectiveness of earthquake relief work and greatly reduce the cost of repairs.
Key words: earthquake; continuous rigid frame bridge; displacement-restricted; bridge pier
0引言
基于性能的抗震设计是指根据建筑物的用途和重要性以及地震设防水准确定建筑物的抗震性能目标,按照该目标进行建筑抗震设计,使设计的建筑在未来可能发生的地震作用下具有预期的抗震性能和安全度,从而将建筑的震害损失控制在预期的范围内。对桥梁而言,是利用桥墩产生塑性铰消耗地震所输入的能量。然而,如何在地震发生后,使整个建筑物乃至整个城市甚至整个社会具有恢复功能,近几年来引起了地震工程界的密切关注与广泛讨论[1]。道路畅通在震后救援中起到了决定性的作用,而桥梁功能即时恢复则在道路畅通中起到关键作用。延性设计方法,虽可避免桥梁倒塌,但塑性铰的永久变形却导致桥墩严重受损,致使地震过后难以即时修复,若塑性铰出现在桥墩中部[2],则更难修复,从而失去灾后亟需的运输功能。研究一种在震后具有恢复功能的桥梁结构,可在震后及时恢复铁路运输功能,保证物资、人员运输,在震后人民生命财产抢救中将起到至关重要的作用,具有非常重要的经济效益和社会效益。
为保证结构的即时恢复功能能力,有学者提出刚体摇晃概念[3]。在早期的摇摆结构中,一般做法为放松结构与基础之间的约束,即上部结构与基础交界面可以受压但几乎没有受拉能力,在水平倾覆力矩作用下,允许上部结构在与基础交界面处发生一定的抬升。地震作用下上部结构的反复抬升和回位就造成了上部结构的摇摆,一方面降低了强地震作用下上部结构本身的延性设计需求,减小了地震破坏,节约了上部结构造价;另一方面,减小了基础在倾覆力矩作用下的抗拉设计需求,节约了基础造价。
根据刚体摇摆概念,有学者提出了地震过后避免桥墩损坏的设计方法,称之为DAD(Damage Avoidance Design)[4-5]。该方法主要将桥墩连接盖梁及基础的钢筋切断,使桥墩在地震时可在期间来回晃动,避免桥墩产生塑性变形而破坏。运用该方法设计的摇晃桥墩系统,在往复地震力作用下,桥墩没有强度或刚度衰退情形。Hao等[6]通过数值方法研究了一座两跨简支梁桥摇摆桥墩的抗震性能,认为可以有效减轻结构的地震响应,减震效果明显。为了使摇摆桥墩在地震作用下具有复位能力从而减小残余变形,研究人员在摇摆桥墩中引入无黏结后张预应力,后张预应力使桥墩与基础交界面处的抗侧力小于传统固定基础桥墩,但大于无预应力的摇摆桥墩,并为桥墩的摇摆提供一定的复位能力。Lee[7]、Palermo等[8]对后张预应力自复位式桥墩的抗震性能进行了研究;Solberg等[9]通过试验对比了摇摆桥墩和传统墩底固结桥墩的抗震性能,认为摇摆桥墩抗震性能优越性明显;Marriott[10]、Palermo[11]、Jeong[12]、郭佳等[13-14]进行了类似的自复位桥梁试验,都认为自复位桥梁在地震中表现出了很好的抗震性能。Astaneh-Asl 和Shen进行了半刚性摇摆桥墩的研究,允许桥墩与基础间有限摇摆,这一研究已用于美国旧金山-奥克兰海湾大桥改造的加固设计中[1]。
铁路连续刚构桥有其特殊性,桥墩刚度大,现有文献未发现专门针对摇摆桥墩在铁路连续刚构桥中的应用研究。而在中国西南地区修建铁路,需要跨越多条地震断裂带,桥址不可避免要位于高烈度地区,因此本文将专门针对大跨铁路桥梁进行研究。
1思路提出
根据摇摆桥墩的概念,本文提出一种限制位移桥墩的思路,构造示意图如图1所示,简述如下:
把桥墩底部设计成一个平台,与承台分离,承台做成凹槽状,而在墩底、承台的顶面预埋钢板,平台在凹槽内可以平动,平动的最大位移量通过平台与凹槽之间的间距进行限制;在凹槽的顶部增加防倾覆装置,防止结构倾覆(尽管这种情况几乎不会出现),在防倾覆装置和承台顶部加塞类似软钢等弹模较低的延性材料(图1中黑色实体部分),对桥墩在凹槽内的转动进行一定程度的限制。这样,桥墩的最大位移量能得到很好的约束。在强地震作用下,桥墩首先发生转动,当水平力大于墩底摩擦力时,桥墩开始滑动。通过桥墩的滑移和转动减小地震能量的输入,同时又能保证最大位移量不超过限制值,地震后保证桥梁的正常通行能力。

1-凹槽状承台;2-防倾覆装置;3-预埋钢板 图1 限制位移桥墩局部构造示意图 Fig.1 Local structure of the displacement-restricted pier
2模型建立
下面以一座3跨铁路连续刚构桥为例,研究上述思路的抗震性能。选用FRAME3D分析软件,该软件在日本工程界抗震分析时广泛应用。选用的桥梁桥跨径布置为72 m+128 m+72 m;主梁为箱型变截面,采用C50混凝土,用弹性梁单元模拟;桥墩为圆端形变截面,墩顶矩形部分长7 m、宽2 m,圆端半径1 m,截面沿墩高方向按1∶40的比例变化,墩身采用C40混凝土,用纤维单元模拟;不考虑地震中桥台发生破坏,选用弹性梁单元模拟。建立的有限元模型如图2所示。下面对模型中采用的材料模型、限制位移的模拟方式进行详细介绍。
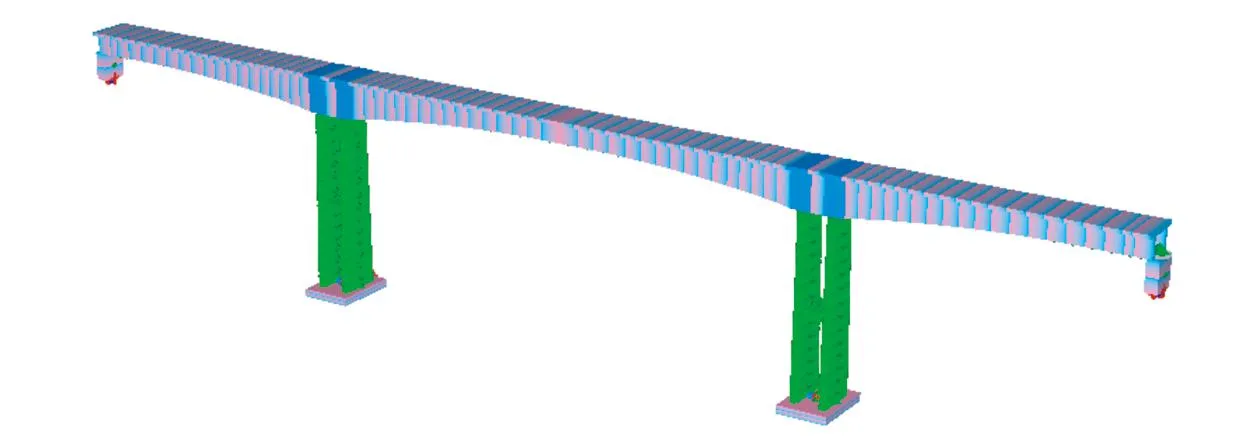
图2 连续刚构桥有限元模型 Fig.2 Finite element model of the continuous rigid frame bridge
2.1材料模型
在钢筋混凝土纤维模型中, 纤维可以划分为三类:保护层混凝土、核心混凝土和钢筋,所以需要定义无约束混凝土、约束混凝土和钢筋三种材料的本构关系模型。对无约束混凝土和约束混凝土均采用Mander单轴混凝土模型,钢筋则选用Menegotto和Pinto建议的修正MP(S-K)模型,本构关系如图3所示。
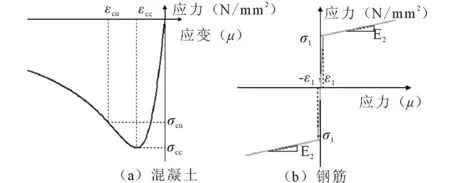
图3 材料本构关系 Fig.3 Constitutive relation of materials
2.2边界条件模拟
对于限制位移的模拟是本次模拟的关键所在,如前所述,既需要保证桥墩底部有不超过设定范围大小的位移量,又要保证桥墩有一定程度的转动能力,同时需要考虑一定的摩擦力,基于此,本文用弹簧单元进行模拟。对于限制位移的水平方向约束,用图4(a)所示的弹簧表示,图中的Gap为预设的限制位移量,达到该值后,桥墩和承台凹槽发生碰撞,用线性刚度模拟,同时设定了破坏位移,即到达该位移后意味着凹槽被撞坏,丧失对桥墩的约束作用;对于竖直方向的约束,用图4(b)所示的弹簧模拟,表示承台只对桥墩向下位移有约束(K2=1×1010kN/m),对桥墩在地震作用下向上抬升不施加约束(K1=0);对于转动方向的约束,采用图4(c)所示的线弹簧进行简单模拟(K1=1×103kN/m);而用图4(d)所示的弹簧模拟墩底与承台顶部之间的摩擦力,可以通过调整墩底和承台顶板预埋钢板的摩擦系数μ调整该摩擦力F(其中F=μN,而N为静力得到的墩底反力),虽然墩底反力在地震中有所变化,但相对于结构自重来说一般小很多,所以简单认为该力保持常数不变。边跨支座采用弹簧模拟,为了保证桥梁在正常使用情况下的横向刚度,只放松纵桥向平动自由度和横桥向转动自由度,约束包括横桥向平动自由度在内的其他方向各自由度,如图4(e)所示。

图4 边界条件 Fig.4 Boundary condition
2.3地震波选取
地震波输入选用Kobe地震波(图5),进行三向地震动输入,水平向加速度峰值调整至0.64 g,即《铁路工程抗震设计规范》规定的Ⅸ度设防烈度区对应的罕遇地震的水平地震基本加速度值。

图5 Kobe地震波 Fig.5 Kobe seismic wave
3计算结果及分析
为了更清楚地了解限制位移桥墩的抗震性能,计算了墩底固结、限制位移量分别为2 cm、5 cm和8 cm四种情况,进行了一个系统的比较。
选取容易形成塑性铰的墩底部位、横系梁处桥墩截面,查看塑性发展情况,这里只列出墩底固结和限制位移量为5 cm时的计算结果(图6、图7)。

图6 墩底固结时截面塑性发展情况 Fig.6 Plastic situation of the section when the bottom of pier is consolidated
从计算结果可以看出,传统墩底固结桥墩经过加强配筋的桥墩墩底、横系梁部位桥墩依次进入塑性,直至墩底部位混凝土到达抗压强度形成塑性铰,在这过程中由于地震作用过于强烈,导致桥墩其他部位混凝土要超过抗压强度的1/3,产生塑性变形;而限制位移桥墩混凝土只在墩底处、横系梁部位产生少量塑性变形,其余部位混凝土基本在弹性变形范围内工作。这表明,限制位移桥墩有非常强的抵御强震的能力,而且在强震中基本能保证桥墩混凝土在弹性范围内工作,这样桥墩几乎没有损伤和破坏,在震后也就不必对桥墩进行修复或只需对个别部位进行简单处理。
再对限制位移量的大小进行一个分析。分别对墩底固结、限制位移量2 cm、限制位移量5 cm、限制位移量8 cm四种情况的横桥向墩底弯矩和横系梁处桥墩弯矩(都取桥墩同一肢的相同位置截面)、墩顶位移进行一个对比(表1)。上述后三种情况下,摩擦力均取值为8 000 kN。

图7 限制位移5 cm时截面塑性发展情况 Fig.7 Plastic situation of the section when the limit displacemenis is 5 m

图8 墩底横桥向反力时程 Fig.8 Transversal counter-force time history of the bottom of pier
从表1看出,限制位移结构体系的墩底弯矩比传统的墩底固结的结构体系减小很多,减小幅度超过2/3;而比较有意思的是,墩顶最大位移不但没有因为桥墩的活动增加,反而降至只有墩底固结墩顶最大位移的约2/3。另外,墩顶最大位移跟限制位移量关系不大,墩底弯矩相差也不大,但横系梁处桥墩弯矩相差较大,说明限制位移量的选择很重要。
接下来再对墩底横桥向的反力进行一个比较。图8分别给出了墩底固结、限制位移量分别为2 cm、5 cm和8 cm时墩底横桥向反力,后面三种情况实际上是桥墩墩底与承台凹槽侧壁之间的碰撞力。可以看出,限制位移桥墩与承台凹槽侧壁之间的碰撞力远大于墩底固结时的反力,但在限制位移量为8 cm时,碰撞力基本已降到限制位移量为2 cm和5 cm时50%的水平。这再一次说明限制位移量的选择很重要,通过选择合适的限制位移量可以减小桥墩墩底与承台凹槽侧壁之间的碰撞力。这里需要说明的是,我们可以采取一些缓冲措施来减小该碰撞力,这将在以后的研究中专门进行分析。
表 1位移、弯矩对比
Table 1Displacement comparison and bending moment comparison

墩底约束方式墩顶位移/mm墩底弯矩/(kN·m)横系梁处桥墩弯矩/(kN·m)墩底固结300.7553298319540限制位移量2cm216.0136135221745限制位移量5cm206.9122045154703限制位移量8cm207.2136419187858
4结论
通过对传统墩底固结结构体系和限制位移桥墩结构体系的对比,可以看到后一种结构体系减震效果明显,基本能保证桥墩在高烈度区罕遇地震作用下保持弹性工作状态。限制位移量的选定对减震效果有一定影响,选择合适的限制位移量可以有效减小墩底弯矩、横系梁处桥墩弯矩,还可以减小桥墩底部与承台限制措施之间的碰撞力,因此在进行设计时可以综合考量,既要考虑减震效果,又要考虑结构在震后快速恢复运输能力的要求。
参考文献(References)
[1] 周颖,吕西林.摇摆结构及自复位结构研究综述[J].建筑结构学报,2011,32(9):1-10.
ZHOU Ying,LU Xi-lin.State-of-the-art on Rocking and Self-centering Structures[J].Journal of Building Structures,2011,32(9):1-10.(in Chinese)
[2] 卢皓,李建中.强震作用下高墩桥梁抗震性能特点分析[J].地震工程学报,2013,35(4):858-865.
LU Hao,LI Jian-zhong.Analysis of Seismic Performance Characteristics of Bridge with High piers Under Strong Earthquake Motion[J].China Earthquake Engineering Journal,2013,35(4):858-865.(in Chinese)
[3] Housner G W.The Behavior of Inverted Pendulum Structures During Earthquakes[J].Bulletin of the Seismological Society of America,1963,53 (2):403-417.
[4] Mander J B,Cheng C T.Seismic Resistance of Bridge Piers Based on Damage Avoidance Based on Damage Avoidance Design[R].Technical Report Nceer,97-0014,Buffalo,NY:NCREE,1997.
[5] Cheng C T.New Paradigms for the Seismic Design and Retrofit of the Bridge Piers[D].Buffalo:State University of New Yorkk at Buffalo,1997.
[6] Hao H,Daube M.Numerical Study of Rocking Pier in Mitigating Bridge Responses to Earthquake Ground Motions[C]//Tweed Heads,Gold Coast:Australian Earthquake Engineering Society 2012 Conference.2012.
[7] Lee W K,Billington S L.Performance-based Earthquake Engineering Assessment of a Self-centering,Post-tensioned Concrete Bridge System[J].Earthquake Engng Struct Dyn,2011,40:887-902.
[8] Palermo A,Pampanin S,Calvi G M.Use of“Controlled Rocking”in the Seismic Design of Bridges[C]//Vancouver,B C, Canada:13th World Conference on Earthquake Engineering.2004.
[9] Solbrg,K M,Mashiko N,Mander J B,et al.Performance of a Damage Protected Highway Bridge Pier Subjected to Bidirectional Earthquake Attack[J].Journal of Structural Engineering,2009,135(5): 469-478.
[10] Marriott D,Palermo A,Pampanin S.Quasi-static and Pseudo-dynamic Testing of Damage Resistant Bridge Piers with Hybrid Connectionss[A]// Proceedings of First European Conference on Earthquake Engineering and Seismology.Geneva,Switzerland,2006.
[11] Palermo A,Pampanin S,Marriott D.Design,Modeling,and Experimental Response of Seismic Resistant Bridge Piers with Posttensioned Dissipating Connections[J].Journal of Structural Engineering,2007,133(11):1648-1661.
[12] Jeong H I,Sakai J,Mahin S A.Shaking Table Tests and Numerical Investigation of Self-centering Reinforced Concrete Bridge Columns[R].Pacific Earthquake Engineering Research Center,2008.
[13] 郭佳. 基于性能的新型自复位桥墩抗震理论与试验研究[D].北京:清华大学,2012.
GUO Jia.Performance Based Research on the Seismic Theory and Test of New Self-centering Pier[D].Beijing:Tsinghua University,2012.(in Chinese)
[14] 郭佳,辛克贵,何铭华, 等.自复位桥梁墩柱结构抗震性能试验研究与分析[J].工程力学,2012,29(增刊);29-34.
GUO Jia,XIN Ke-gui,HE Ming-hua,et al.Experimental Study and Analysis on the Seismic Performance of a Self-centering Bridge Pier[J].Engineering Mechanics,2012,29(S):29-34. (in Chinese)

