受噪声影响的复拟随机样本的STL关键定理

受噪声影响的复拟随机样本的STL关键定理

杜二玲1，李俊华2

(1.中国地质大学长城学院 基础课教学部，河北 保定071000；2.河北大学 数学与信息科学学院，河北 保定071002)

摘要：引入了拟概率空间上复拟随机样本受噪声影响的复经验风险泛函、复期望风险泛函、复经验风险最小化原则以及严格一致性的定义，提出并证明了拟概率空间上复拟随机样本受噪声影响的学习理论关键定理，为系统建立拟概率空间上基于噪声影响的复拟随机样本的统计学习理论奠定了基础.

关键词：复拟随机样本；噪声；复经验风险最小化原则；关键定理

DOI：10.3969/j.issn.1000-1565.2015.05.001

中图分类号：O29;TP181文献标志码:A

收稿日期：2014-11-30

基金项目：河北省教育厅科研项目(QN20131055)；河北省高等学校科学技术研究项目(Z2013038)

Key theorem of statistical learning theory with complex

quasi-random samples corrupted by noise

DU Erling1, LI Junhua2

(1. Basic Teaching Department, China University of Geosciences Great Wall College, Baoding 071000,

China;2. College of Mathematics and Information Science, Hebei University, Baoding 071002, China)

Abstract:Some new concepts, such as complex empirical risk functional, complex expected risk functional, complex empirical risk minimization principle, and strict consistency built on quasi-probability space and based on complex quasi-random samples corrupted by noise are introduced. The key theorem of learning theory is given and proved on quasi-probability space and based on complex quasi-random samples corrupted by noise. The investigations will help lay essential theoretical foundations for the systematic and comprehensive development of the complex quasi-random samples corrupted by noise.

Key words: complex quasi-random samples; noise; complex empirical risk minimization principle; key theorem

MSC 2010: 28B99

第一作者：杜二玲(1975-)，女，河北安国人，中国地质大学长城学院讲师，主要从事不确定统计学习理论.

E-mail:duerling@126.com

统计学习理论(statistical learning theory, SLT)是Vapnik等[1-2]在20世纪60年代末提出,于90年代中期发展较成熟, 被学术界公认为较好地处理小样本的学习理论. SLT是建立在概率空间上且所研究的样本是实随机样本. 而概率的可加性条件非常强, 现实中还存在大量的非实随机样本. 为此, 一些学者已经开始从事非概率空间上和复随机样本的统计学习理论的研究, 得到了一些重要的成果[3-10].其次, SLT所研究的样本总是事先假定不受外界干扰.这种假定在实际应用中往往得不到满足. 噪声是影响样本的因素之一，也是人们考虑比较多的一种, 有学者开始了样本受到噪声影响的统计学习理论的研究[11-13].基于上述考虑, 本文在拟概率空间上引入了复拟随机样本受噪声影响的一些基本定义, 讨论了复拟随机样本受噪声影响的学习理论的关键定理, 从而扩大了支持向量机等应用性研究领域的理论基础, 拓展了统计学习理论的应用范围.

1基本概念

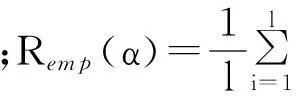
定义1设Q′(z,α)=Q(z,α)+ξ是考虑噪声之后的损失函数,ξ1,ξ2,…,ξl与ξ是独立同分布的, 定义拟概率空间上复拟随机样本受等均值噪声影响的复期望风险泛函为

R′(α)=E[Q′(z,α)]=E[Q(z,α)+ξ]=E(Q(z,α))+p=R(α)+p.

拟概率空间上复拟随机样本受等均值噪声影响的复经验风险泛函为

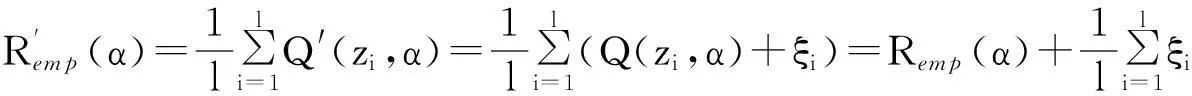
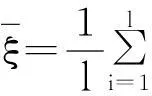
定义2假设复期望风险泛函的最小值在Q′(z,α0)上取得,复经验风险泛函的最小值在Q′(z,αl)取得.用Q′(z,αl)逼近Q′(z,α0)的值. 这种在拟概率空间上解决最小化复期望风险泛函问题的方法被称为复经验风险最小化原则(CERM原则).

定义3对于拟概率空间上的复可测函数集Q′(z,α),α∈Λ和拟概率μ,如果对于该函数集的任何非空子集Λ(c)={α:‖R′(α)‖≥c},c∈(-∞,∞)和任意ε>0,收敛性

(1)

成立，则称复经验风险最小化原则对于拟概率空间上的复可测函数集Q′(z,α),α∈Λ和拟概率μ是严格(非平凡)一致的.

定义4对于拟概率空间上的复可测函数集Q′(z,α),α∈Λ和拟概率μ,如果对于任意ε>0,

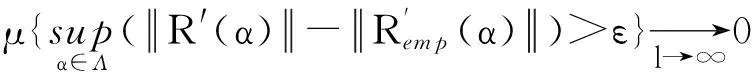
(2)

则称式(2)为在拟概率空间中的给定复可测函数集上复经验风险泛函到复期望风险泛函的一致单边收敛性.

2主要结论

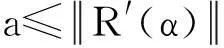
1)对于给定的拟概率μ,复经验风险最小化方法对拟概率空间上的复可测函数集Q′(z,α),α∈Λ严格一致成立.

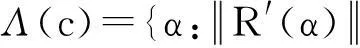
定理第1部分得证.

下面证明充分性. 假设一致单边收敛性式(2)成立.

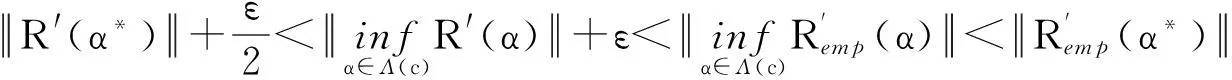
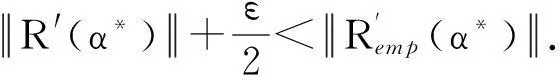
(3)

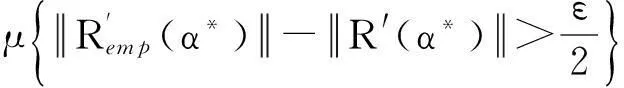
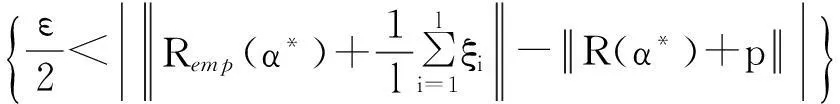
因此B⊆(B1∪B2).由大数定理知μ(B1)→0, 由契比雪夫不等式知μ(B2)→0,所以

μ(B)<μ(B1∪B2)→0，

由式(3)得到μ(A1)→0.

(4)

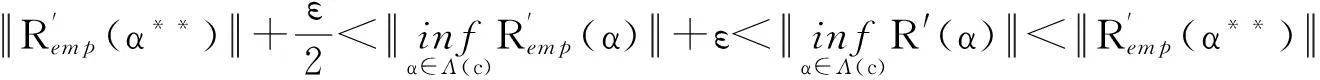
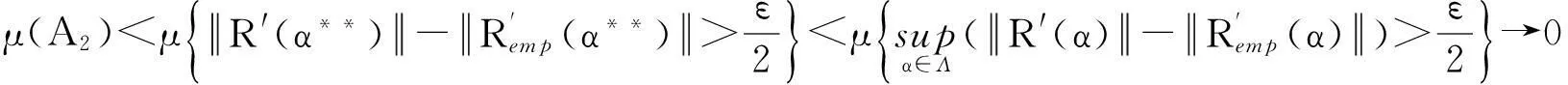
(5)

根据式(4)，(5)得μ(A)=μ(A1∪A2)→0.定理得证.

参考文献:

[1]VAPNIK V N. Statistical learning theory[M]. New York: A Wiley-Interscience Publication, 1998.

[2]VAPNIK V N. An overview of statistical learning theory[J]. IEEE Transactions on Networks, 1999, 10(5):.

[3]SUN Xiaojing, WANG Chao, HA Minghu, et al. The key theorem of learning theory based on hybrid variable [Z]. Proceedings of the International Conference on Machine Learning and Cybernetics, Guilin, 2011.

[4]YAN Shujing, HA Minghu, ZHANG Xiankun, et al. The key theorem of learning theory on uncertainty space[J]. Sixth International Symposium Neural Networks, 2009(6): 27-29.

[5]HA Minghu, BAI Yunchao，WANG Peng. The key theorem and the bounds on the rate of uniform convergence of statistical learning theory on a credibility space[J]. Advances in Fuzzy Sets and Systems, 2006, 1(2): 143-172.

[6]张植明, 田景峰, 哈明虎. 基于复拟随机样本的统计学习理论的理论基础[J]. 计算机工程与应用, 2008, 44(9): 82-86.

ZHANG Zhiming, TIAN Jingfeng, HA Minghu. Theoretical foundations of statistical learning theory of complex quasi-random samples[J]. Computer Engineering and Application, 2008, 44(9): 82-86.

[7]HA Minghu, PEDRYCZ W, ZHANG Zhiming, et al. The theoretical foundations of statistical learning theory of complex random samples[J]. Far East Journal of Applied Mathematics, 2009, 34(3): 315-336.

[8]HA Minghu, LI Yan, LI Jia, et al. The key theorem and the bounds on the rate of uniform convergence of learning theory on Sugeno measure space[J]. Science in China, Series F Information Sciences, 2006, 49(3): 372-385.

[9]周彩丽, 哈明虎, 鲍俊艳, 等. 基于模糊数的模糊学习理论的关键定理[J]. 河北大学学报：自然科学版, 2008, 28(5): 449-451.

ZHOU Caili, HA Minghu, BAO Junyan, et al. Key theorem of learning theory based on fuzzy number[J]. Journal of Hebei University：Natural Science Edition, 2008, 28(5): 449-451.

[10]哈明虎, 冯志芳, 宋士吉, 等. 拟概率空间上学习理论的关键定理和学习过程一致收敛速度的界[J]. 计算机学报, 2008, 31(3): 476-485.

HA Minghu, FENG Zhifang, SONG Shiji, et al. The key theorem and the bounds on the rate of uniform convergence of learning theory on quasi-probability spaces[J]. Chinese Journal of Computers, 2008, 31(3): 476-485.

[11]李俊华, 高林庆, 李海军. 噪声影响的泛空间上的学习理论关键定理[J]. 计算机工程与应用, 2012, 48(27): 49-52.

LI Junhua, GAO Linqing, LI Haijun. Key theorem of learning theory with samples corrupted by noise on pan-space[J]. Computer Engineering and Application, 2012, 48(27): 49-52.

[12]哈明虎, 李俊华, 白云超，等. 样本受零均值噪声影响下的学习理论的若干理论研究[J]. 自然科学进展， 2006(12): 1668-1673.

HA Minghu, LI Junhua, BAI Yunchao, et al. Several influence theoretical research of learning theory with samples corrupted by zero-mean noise[J]. Progress in natural science, 2006(12): 1668-1673.

[13]李俊华, 李海军. 受噪声影响的复hybrid样本的学习理论关键定理[J]. 河北大学学报:自然科学版, 2014, 34(1): 14-18.

LI Junhua, LI Haijun. Key theorem of learning theory with complex hybrid samples corrupted by noise[J]. Journal of Hebei University：Natural Science Edition, 2014, 34(1): 14-18.

(责任编辑：王兰英)