临床检验质量控制程序的性能验证*

张诗诗，王 薇，王治国(北京医院 国家老年医学中心 卫生部临床检验中心，北京 100730)

1 质量控制性能验证的概述

随着实验室质量控制(QC，简称质控)计划的发展和风险管理的引入，许多不同类型的QC可以用于操控分析过程的性能并及时准确地检出可能发生的任意误差。因此，进一步验证这些QC程序的有效性对于提升实验室管理水平是至关重要的。

首先，验证实验室是否有一个合理的质控策略。传统上，验证质控策略集中于评价其是否有足够的功效去检出任何“关键的”失控状态(指≥5%的检验结果处于不可接受的状态)[1，2]。

其次，定义性能度量。在风险管理的时代，要求用不同的性能度量来判定QC策略的功效。关于特定的QC策略在失控时是如何影响患者标本的检验，即为探讨其由于失控条件而产生的不可靠患者结果预期数E(Nu)。因为不知道即将发生的失控状态达到何种程度以及各程度的失控状态产生的不同E(Nu)，所以QC验证问题变成“任何程度的失控状态产生的E(Nu)是否可以接受？”[3]。

本文重点在于，针对给定的质控策略，如何计算E(Nu)以及如何用它来验证质控策略的可接受性[4]。质控策略包括每次质控中评估的质控样本数、质控频率(或质控活动之间被评估的患者样本平均数)和质控规则，目的是用于检出在控分析系统的改变。根据系统失控时产生额外的不可靠结果数高于在控时产生的不可靠结果数，可以测量质控策略的功效。

2 质量规范

2.1 允许总误差(TEa) 虽然指定一个可将结果分为接受或不可接受的质量规范需要投入大量的工作[5，6]；但实际的重点在于可运用它来验证质控程序。本文中我们使用表达为百分数的TEa。TEa通常是指定的单一值或在不同浓度下分别给出的不同值，但关键是TEa需要反映出所要求的质量。

当标本检测结果的报告值与其真值有差别并超过TEa时，该结果被认为是不可靠的。虽然分析过程始终存在一些固有分析误差使得标本结果的真值难以确定，但在理想的情况下，当分析系统在控时，固有分析误差的大小与TEa相比是很小的。

2.2 西格玛(σ)度量 σ是利用偏倚调整TEa之后与稳定的在控分析不精密度的比值(如公式)。σ可用于评价分析系统在控操作期间产生不可靠结果的几率有多大[7]，因为即使分析系统处于在控状态，也有一定的产生不可靠结果的概率。σ也是判断分析过程在失控状态下有多大耐受程度的一种简便方法。见图1，若1 000 000个患者标本在失控条件出现时采用6σ过程进行评估，且失控条件会在评估过程中产生2σ偏倚，则预期有32个结果是不可靠的；若1 000 000个患者标本在失控条件出现时采用2σ过程进行评估，且失控条件会在评估过程中产生2σ偏倚，则预期有454 531个结果是不可靠的。

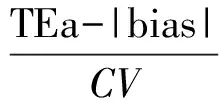
σ越低，对于给定的失控条件将会有更高的E(Nu)。通常，低σ过程比高σ过程要求更多的质控资源来产生相等的E(Nu)。

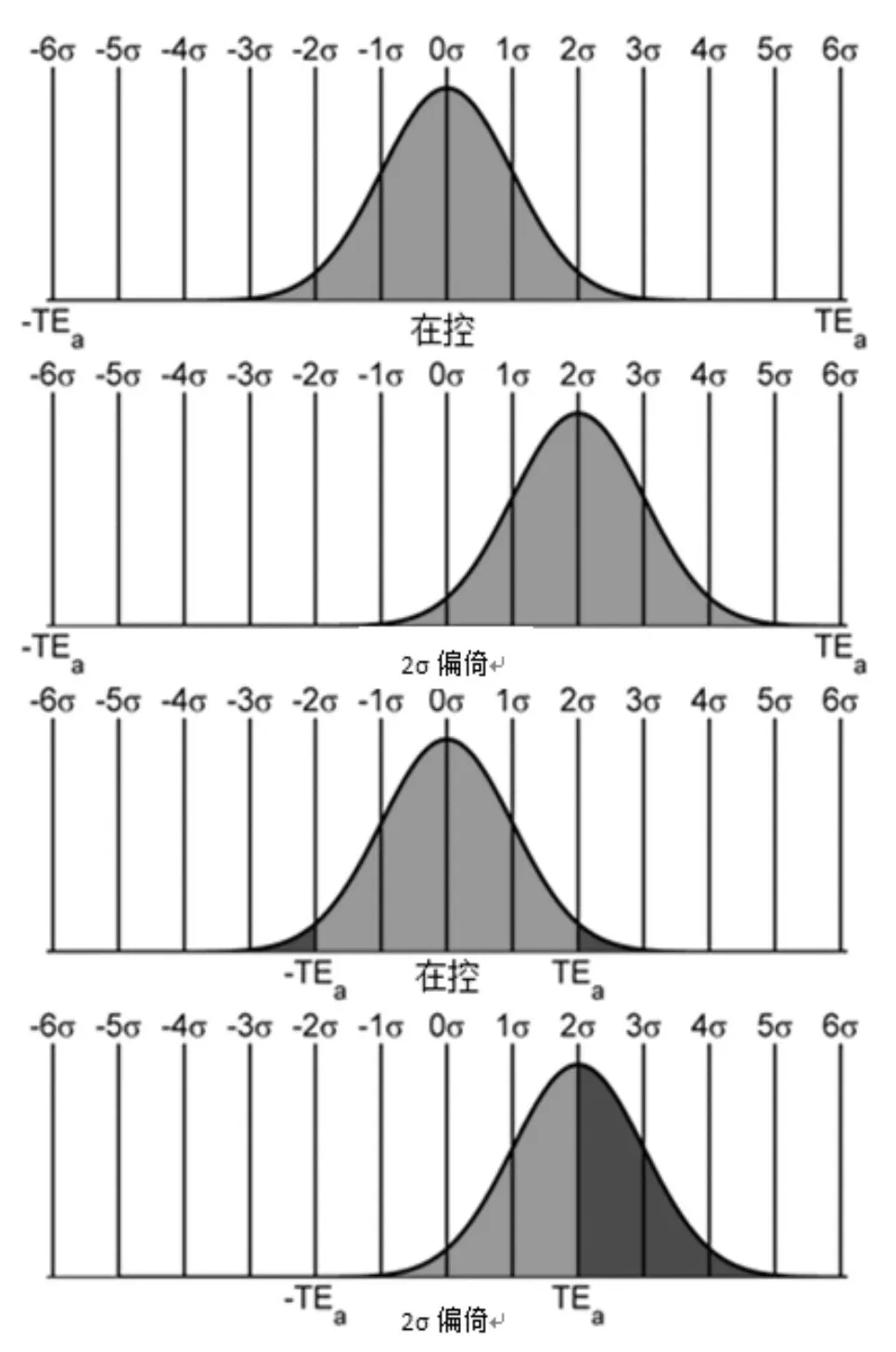
图1 6σ过程和2σ过程

顶部的2张测量误差分布图显示了采用允许TEa为±6σ的一个在控过程和一个带有2σ偏倚的失控过程。底部的2张测量误差分布图显示了采用TEa为±2σ的一个在控过程和一个带有2σ偏倚的失控过程。浅色阴影面积表示产生结果符合明确质量要求的概率，深色阴影面积表示产生结果不符合明确质量要求的概率。

3 失控检出

3.1 失控和在控状态产生不可靠结果的概率差(ΔPE) 一般认为，失控严重的状态产生不可靠结果的可能性高，而失控微小的状态对产生不可靠的结果几乎没有影响。当分析系统处于在控状态时可以计算产生不可靠结果的概率，当失控条件的大小被给出时也可以计算产生不可靠结果的概率，且二者的概率差可以表示为ΔPE。

见图2，当分析过程在控时，SE=0，ΔPE=0；对于足够严重的失控状态，ΔPE会接近1。计算失控状态的ΔPE，若失控范围从0(在控)到1.5倍TEa(1.5*4σ=6σ)，将产生一个从0过渡到接近于1的ΔPE曲线作为评估失控状态严重程度的函数。

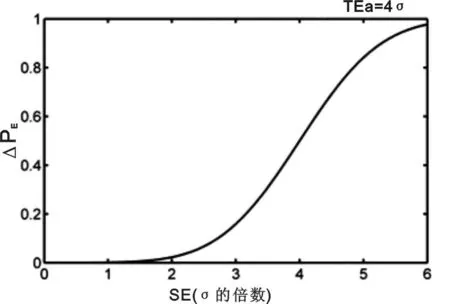
图2 ΔPE曲线

SE代表失控状态的系统误差，以过程稳定的分析不精密度(σ)的倍数表示。ΔPE表示产生不符合规定TEa的患者结果的概率变化。

3.2 误差检出概率(Ped) 针对已明确严重程度的失控状态，运用质控规则判断其为失控的概率称为该质控规则的误差检出功效，即误差检出概率，表示为Ped。

检出已明确严重程度的失控状态需要进行的质控活动预期(或平均)数与Ped有关，呈反比关系；即Ped越高，检出失控状态所要求的质控活动平均数越低。对于任意给定的质控规则和失控状态严重程度，检出失控的质控活动平均数是1/Ped。

不同的质控规则有不同的功效曲线[8～10]。如图3，对于2σ偏倚的失控状态，质控规则判断失控的概率大约是40%(Ped=0.4)，因此，平均要用2.5次的质控活动(1/Ped=1/0.4)来检出分析检测系统中的2σ失控偏倚。

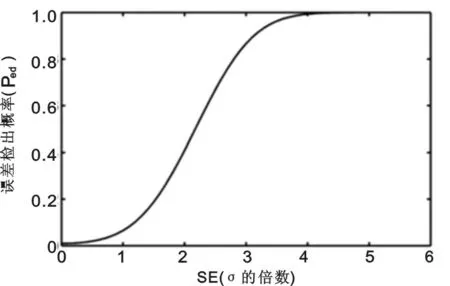
图3 误差检出概率(Ped)

具有2个浓度水平质控品13s/22s/R4s多规则质控的功效曲线[8]，横轴SE代表失控状态的系统误差，以σ的倍数表示。SE=0意味着分析过程处于在控状态。纵轴代表质控规则判断失控的概率，作为评价失控状态严重程度的函数。

3.3 受影响患者的预期数(ANPaffected) 将1/Ped与质控活动之间检查患者样品的平均数相结合，在识别和解决持续失控状态之前，可以预测有多少患者样本受影响，即受影响患者的预期数ANPaffected[11]与质控活动之间的受检患者样本平均数呈正比，与质控频率呈反比。

当分析系统在控时(SE=0)，ANPaffected很大，反映了质控规则在假失控(在无失控状态时质控规则判断为失控)之间所评估的患者样品数。见图4，质控规则假失控率大约是0.01，期望平均每100次质控活动发生1次质控规则假失控，且在质控活动之间平均检测100个患者样本，则在控系统在该质控规则假失控之间的ANPaffected是100×100=10 000。

图4 受影响患者的预期数(ANPaffected)

失控程度越严重，质控规则的Ped越大且1/Ped越小，导致ANPaffected也越小。对于足够严重的失控状态，在出现失控状态后的第一次评估，将确保质控规则判断为失控。假设在检测过程中的任意时刻失控状态有相同的发生概率，当极严重的失控状态在其发生后的第一次质控活动中被检出时，ANPaffected将是质控活动间所评估的患者样本平均数的一半。

ANPaffected可作为评价失控状态严重程度的函数[11]。横轴SE代表失控状态的系统误差，以σ的倍数表示。SE=0意味着分析过程处于在控状态。纵轴表示ANPaffected，以对数刻度表示。

4 E(Nu)的划分和运用

4.1 E(Nu)的划分 E(Nu)是由于失控状态而产生的不可靠患者结果预期数，它是△PE和ANPaffected的积[12，13]。对于严重的失控状态，一般经验规则是E(Nu)为质控活动之间患者数量的一半[14]。

E(Nu)提供了一种度量，直接描述产生患者结果的可靠性以及质控策略受给定严重程度的失控状态影响的性能之间的关系，且可以进一步分成两部分。在失控状态发生和最后可接受的质控之前所产生的不可靠结果被认为是不能识别和纠正的“最终的”结果，其预期数缩写为E(Nuf) 。在最后可接受的质控之后所产生的不可靠结果由于大部分是近期产生的则被认为是“可纠正的”结果，其预期数缩写为E(Nuc)。图5中E(Nuf)=9(从发生失控状态到最后的可接受质控之间有9个红色星号)及E(Nuc)=4(最后的可接受质控和质控判断为失控之间有4个红色星号)。

向上移动的线代表失控状态，水平线代表随时间变化的分析过程；每条垂直线代表一次患者样本检测。每个菱形代表一次质控活动；绿色菱形代表质控在控，红色菱形代表质控失控。红色星号代表不可靠的患者样本结果。

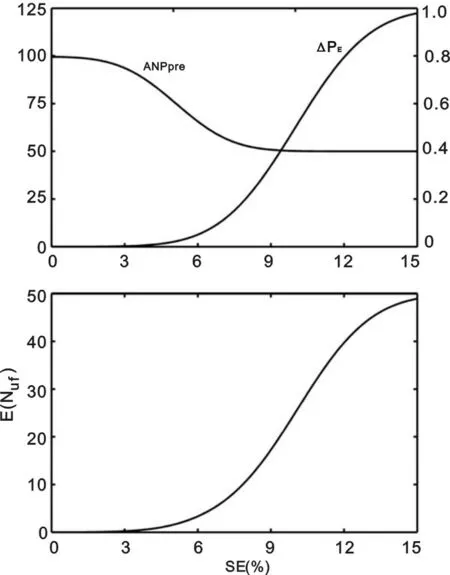
4.2 运用 E(Nuf)是ANPpre(发生失控状态和最后的可接受质控活动之间受影响患者的预期数)和△PE之积(见图6)。E(Nuf)对于非常微小和非常严重的失控状态均很小，并且在非常微小和非常严重的失控状态之间的某处获得最大值。若最大的E(Nuf)值被认为是可接受的，则对于任意的失控情况，质控策略可以保证实验室质量；若最大的E(Nuf)值被认为是不可接受的，则应该检查和调整质控策略，直到实现可接受的最大E(Nuf)。SE代表失控状态系统误差的大小，以百分数表示。

SE代表失控状态系统误差的大小，以百分数表示。

E(Nuc)是ANPpost(最后的可接受质控活动和质控活动判断为失控之间受影响患者的预期数)与△PE之积(见图7)。ANPpost依赖于失控状态发生后的第一次质控活动能否检出失控情况。如果失控状态在其发生后的第一次质控活动中未被检测出，那么在最后的可接受质控活动和质控活动判断为失控之间所有的患者样本将受失控状态的影响。如果失控状态在其发生后的第一次质控活动中被检测出，那么如上文所述，我们预期在质控活动之间被检测的患者样本平均数有一半会受到影响[11]。SE代表失控状态系统误差的大小，以百分数表示。

SE代表失控状态系统误差的大小，以百分数表示。

最大的E(Nuc)值将总是接近于质控活动之间被检测患者样本平均数的一半。实验室在失控状态被识别和解决后，需要及时纠正最大的E(Nuc)值，以阻止不可靠的患者结果在发生严重的失控状态时被不合理地运用。若实验室有到位的程序可以及时识别、重复和纠正最大的E(Nuc)且使其达到质控活动之间被检测的患者样本平均数的一半，那么最大的E(Nuc)值是可以接受的。否则，应该采取措施，如改变质控频率来减少最大的E(Nuc)值。

5 总结

质控策略是由质控过程中所评估的质控物样本数，质控规则以及质控频率(质控活动之间被评估的患者样本平均数)所组成。通过对E(Nu)的划分并计算最大的E(Nuf)和E(Nuc)值以及确定它们是否被实验室接受，进一步验证临床实验室质控策略的合理性。

若最大的E(Nuf)值太高，可以通过增加质控过程中被评估的质控物样本数，使用有更高Ped的质控规则，或者减少质控活动之间被评估的患者样本数三者相结合，由此改变质控策略来减少E(Nuf)值；也可以通过减少分析系统不精密度或增加TEa规范(任选一个)来减少其值。

最大的E(Nuc)值依赖于质控活动之间被测的患者样本平均数。如果最大的E(Nuc)值太高，就要降低质控活动之间被评估的患者样本数。

[1] Westgard JO．How to establish control limits．In：Assuring the right quality right[C]．Madison (WI)：Westgard QC，Inc，2007：245-259．

[2] Brooks ZC．Choosing our own rules．In：Performance-driven quality control[C]．Washington，DC：AACC Press，2001：89-114．

[3] Parvin CA．Quality-control (QC) performance measures and the QC planning process[J]．Clin Chem，1997，43(4)：602-607．

[4] Parvin CA．Statistical topics in the laboratory sciences[J]．Methods in Molecular Biology，2007(404)：353-375．

[5] Kenny D，Fraser CG，Hyltoft petersen P，et al．Consensus agreement[J]．Scand J Clin Lab Invest，1999，59(7)：585．

[6] Fraser CG．Quality specifications．In：Biological variation：from principles to practice[C]．Washington，DC：AACC Press，2001：29-66．

[7] Westgard JO．How to use sigma-metrics QC selection tool．In：Assuring the right quality right[J]．Madison (WI)：Westgard QC，Inc，2007：125-146．

[8] Parvin CA．Assessing the impact of the frequency of quality control testing on the quality of reported patient results[J]．Clin Chem，2008，54(12)：2049-2054．

[9] Yundt-Pacheco JC,Parvin CA．The impact of QC frequency on patient results[J]．MLO Med Lab Obs，2008，40(9)：24,26-27．

[10] Cembrowski GS，Carey RN．Quality control procedures．In：Laboratory quality management[J]．Chicago：ASCP Press，1989：59-79．

[11] Parvin CA．Comparing the power of quality-control rules to detect persistent systematic error[J]．Clin Chem，1992，38(3)：358-363．

[12] Parvin CA．Comparing the power of quality-control rules to detect persistent increases in random error[J]．Clin Chem，1992，38(3)：364-369．

[13] Parvin CA，Kuchipudi LS，Yundt-Pacheco JC．Should I repeat my 1∶2s QC rejection?[J]．Clin Chem，2012，58(5)：925-929．

[14] Parvin CA．New insight into the comparative power of quality-control rules that use control observations within a single analytical run[J]．Clin Chem，1993，39(3)：440-447．