大型柔性整流罩分离特点仿真分析

大型柔性整流罩分离特点仿真分析

张大鹏1，雷勇军1，柳海龙2，唐霄汉2

(1. 国防科学技术大学航天科学与工程学院，长沙410073；2. 北京宇航系统工程研究所，北京100076)

摘要：建立整流罩刚体及弹性体有限元模型，联合大型商用软件MSC.Nastran及LS-DYNA对新一代大型运载火箭整流罩分离过程进行仿真分析。通过与刚体模型对比，分析分离过程中整流罩自由模态、变形特点、运动轨迹、能量变化及呼吸运动对分离角速度、罩内可用包络空间的影响。结果表明，整流罩呼吸运动对罩内可用包络空间影响最大区域为后柱段下端，对整流罩质心运动轨迹影响较小，能明显减小过顶角速度及脱钩角速度，使过顶、脱钩时间有所延迟，致分离弹簧势能损失约36%。结论可为整流罩分离系统优化设计、提高整流罩分离可靠性等提供重要参考。

关键词：运载火箭；整流罩；分离；LS-DYNA；有限元分析

中图分类号:V421.3文献标志码：A

Simulations and analyses on separation characteristics of large scale flexible fairing

ZHANGDa-peng1,LEIYong-jun1,LIUHai-long2,TANGXiao-han2(1. College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China; 2. Beijing Institute of Aerospace Systems Engineering, Beijing 100076, China)

Abstract:The rigid and flexible finite element models of a large scale flexible fairing were established. Then the separation of fairing in a new generation launch vehicle was simulated by using combinedly the softwares MSC. Nastran and LS-DYNA．Comparing with the results by the rigid model，the elastic deformation of fairing, its motion trail as well as its energy consumption in the process of separation were analyzed. Besides, the effect of elastic vibration on the separation angular velocity and available envelope space were discussed. The results demonstrate that the available envelope space influenced most significantly by elastic vibration is at the end region of the colum and the elastic vibration has little influence on the displacements of fairing centroid. It also shows that the separation angular velocity will decrease due to elastic vibration when the fairing centroid is passing through the top or the fairing is being unhooked from the launch vehicle and at that time, 36 percent elastic potential energy of the spring is wasted．These conclusions can provide important reference to the structural optimization of fairing separation system and the improvement of reliability of the separation process．

Key words:launch vehicle; fairing; separation; LS-DYNA; finite element analysis

整流罩作为运载火箭有效载荷的保护装置，可使其飞行时防止有效载荷受气动力、气动热及声振等环境因素影响，提供良好环境[1]。运载火箭飞出大气层后整流罩任务完成，需抛掉。为保证整流罩安全分离，须以一定过顶角速度或平抛速度完全脱离箭体，并与箭体保持足够分离距离。为此在整流罩研制中须研究其运动姿态、分离轨迹及罩内包络空间等。而整流罩分离过程仿真分析为研制的重要环节，分析结果可为分离系统及其它相关结构优化设计提供重要依据[2]。

早期整流罩分离仿真研究主要将柔性多体动力学模型退化为多刚体动力学及结构动力学模型进行分析[3]。由于整流罩分离过程中伴随罩体的“呼吸运动”(即弹性变形)，而刚体模型无法分析整流罩弹性变形及呼吸运动对分离特点影响，用其对整流罩分离仿真分析存在较大局限性。目前呼吸运动对整流罩运动姿态、分离轨迹及罩内包络空间等影响研究较少[3-6]。而新一代大型运载火箭5.2 m直径整流罩研制，使呼吸运动对整流罩分离特点影响研究更加迫切。复合材料蜂窝夹层结构的使用也给相关分析带来较大难度。通过研究呼吸运动对分离特点影响作用，对抑制呼吸运动、提高弹簧能量利用率及相关地面试验等具有重要意义。

柔性多体动力学及有限元分析软件为系统分析大型柔性整流罩分离提供基础。本文利用大型商用软件MSC.Nastran及LS-DYNA对整流罩分离过程进行仿真分析。通过对比刚体、弹性模型仿真结果，分析呼吸运动对大型柔性整流罩分离影响。

1柔性整流罩仿真分析模型

1.1柔性多体系统动力学控制方程

柔性整流罩分离过程的动力学属于柔性多体动力学，建模方法包括弹性动力学方法(Kineto-Elastodynamics,KED)及柔性多体动力学方法(Flexible Multibody Dynamics,FMD)两种[7]。本文利用FMD对柔性整流罩分离过程进行仿真分析[8]。

惯性坐标系OXYZ下柔性多体系统见图1，其中o′x′y′z′为柔性体的固连动坐标系。柔性体点P的位置向量rp为

(1)

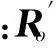
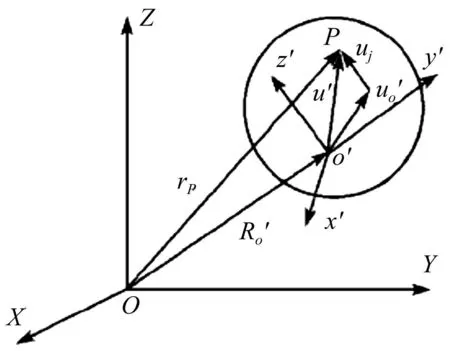
图1　柔性多体系统 Fig.1 FMD system

利用模态综合法对变形向量uf进行离散，即

uf=Φqf

(2)

式中：Ф为柔性体模态矩阵；qf为变形广义坐标。式(1)对时间一阶导数为柔性体P点速度向量，即

(3)

(4)

式中：B=B(P,u′)。

式(3)对时间求一阶导数为柔性体P点加速度向量，即

(5)

柔性体动能为

(6)

式中：ρ为柔性体质量密度；V为柔性体体积； q=[R′ToPTqTf]为广义坐标；M为柔性体质量矩阵。

柔性体因弹性变形引起弹性力虚功为

-qTfKffδqf=Qeδqf

(7)

式中：Qe为由弹性变形引起的广义力。

利用Lagrange法建立自由柔性体动力学控制方程为

(8)

通过Lagrange乘子法，得柔性多体系统动力学控制方程及系统约束方程为

(9)

式中：λ为Lagrange乘子向量。

1.2大型柔性整流罩仿真模型

本文整流罩采用剥离式分离的蚌式结构，沿纵向为对称两半罩，由爆炸螺栓或无污染导爆索连接成受力整体，下端与仪器舱由爆炸螺栓或爆炸索连接。分离时在整流罩下端两侧分离弹簧力推动下两半罩各自绕底部铰链旋转，至一定角度后铰链与下耳片脱钩，两半罩与箭体完全分离。建立基于FMD理论的整流罩分离仿真分析模型，分析研究柔性整流罩分离过程。整流罩主要结构包括端头帽、前锥段及前后柱段等。据各部结构特点用MSC.Patran软件建模，其中蒙皮等薄壁结构用四节点壳单元，前锥段及前柱段夹芯结构用六面体单元，弹簧用Bar单元，非结构质量用质量单元模拟，有限元模型各结构间用共节点方式连接。整流罩半罩有限元模型见图 2，共有单元21 631个，节点21 217个。

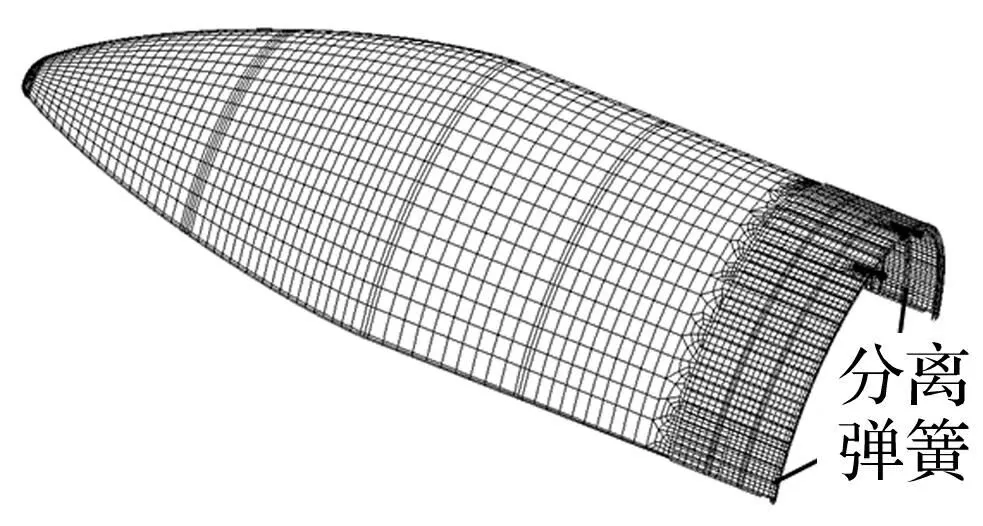
图2　整流罩半罩有限元模型 Fig.2 FEM model of half fairing

弹性模型中，用LS-DYNA中3号材料*MAT_ PLASTIC_KINEMATIC模拟整流罩中金属等各向同性材料特性，蜂窝夹芯结构用LS-DYNA中22号材料*MAT_COMPOSITE_DAMAGE模拟。相对整流罩本体而言，铰链及下耳片结构刚度较大，故用刚体材料即20号*MAT_RIGID模拟。用S01号材料*MAT_SPRING_ELASTIC模拟整流罩分离弹簧。整流罩在分离过程中存在过载系数1.01的恒定过载。对弹簧下端及下耳片整体节点六个自由度施加约束，并在铰链与下耳片间定义自动面接触。整流罩分离旋转铰链机构模型见图 3。

整流罩有限元模型建立后，利用MSC.Nastran软件分析整流罩自由模态[9-10]。整流罩非刚体运动前4阶模态(第7～10阶)见图 4[11]。

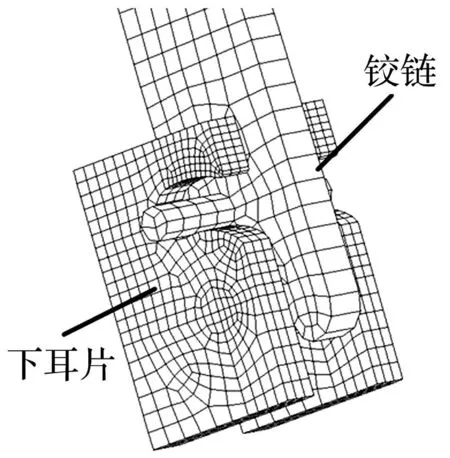
图3　整流罩分离旋转铰链机构模型 Fig.3 FEM model of hinge mechanism for rotating separation

图4　整流罩部分振型 Fig.4 Some modal shapes of fairing

2整流罩分离动力学分析

在所建大型柔性整流罩有限元模型基础上，利用非线性动力分析有限元软件LS-DYNA分析分离过程中整流罩变形特点、运动轨迹及呼吸运动对分离过程影响[12]。

2.1整流罩运动轨迹及变形特点分析

整流罩分离过程中运动姿态及变形特点见图 5。由图5看出，在弹簧作用下整流罩绕旋转铰链转动并达到过顶位置后继续转动，达一定角度后铰链与下耳片脱钩分离，整流罩完成分离动作。整流罩分离中伴随明显的呼吸运动，后柱段下端及前柱段与前锥段对接处情况最严重。

图5　整流罩分离过程 Fig.5 The course of fairing separation

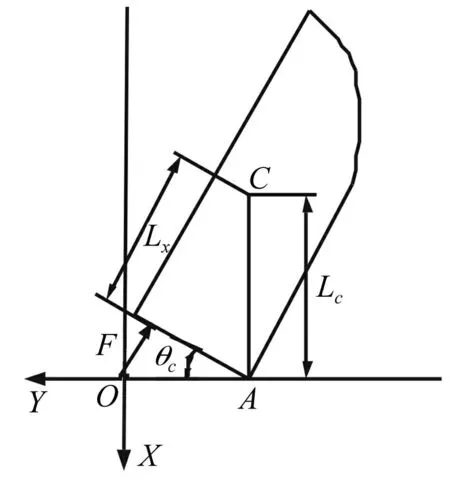
图6　半罩运动分析坐标系 Fig.6 Coordinate system for movement analysis

整流罩分离过程的运动轨迹可通过质心各向位移变化体现，见图 6。图中OX轴沿分离前半罩纵向分离面，OY轴与分离前半罩横向分离面平行，A为铰链旋转点，C为整流罩半罩质心位置。

质心在X向位移变化见图7。由图7知，分离初始，整流罩质心在弹簧力作用下沿X轴负向移动，当达过顶处(X向位移最小值)后逐渐沿X轴正向移动。整流罩质心在Y轴、Z轴的位移变化见图8、图9。由两图看出，分离中整流罩质心沿Y轴负向逐渐远离纵向分离面，且因对称，在Z向0附近上下波动。而在惯性系下质心的位移变化曲线仅体现出整流罩整体运动特点，未体现呼吸运动对质心位移变化影响，说明呼吸运动对整流罩质心位移变化影响不明显。

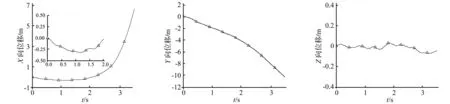
图7 质心X向位移变化曲线Fig.7Xdisplacementcurveoffairingcentroid图8 质心Y向位移变化曲线Fig.8Ydisplacementcurveoffairingcentroid图9 质心Z向位移变化曲线Fig.9Zdisplacementcurveoffairingcentroid

2.2呼吸运动对分离角速度影响分析

整流罩按刚体模型计算时不考虑其本身呼吸运动影响，弹簧势能全部转化为整流罩动能，利用能量守恒定律推导刚体模型的理论过顶角速度。整流罩半罩在XOY平面内刚体运动(图6)，由能量守恒定律知

Q+V=T

(10)

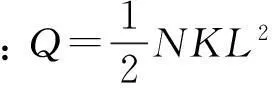
(11)

由式(11)可得

(12)

式中：N为整流罩半罩弹簧个数；K为弹簧系数；L为弹簧初始压缩量；M为半罩质量；k为过载系数；Vc为过顶时质心速度；Ic为质心轴转动惯量；ωc为过顶角速度。

整流罩分离角速度变化曲线见图 10。由刚体模型角速度的变化曲线看出，在弹簧推动下整流罩分离角速度逐渐增大；弹簧力释放完后由于过载做负功分离角速度有所减小。整流罩达到过顶位置后分离角速度在过载作用下逐渐增大，达到脱钩位置后分离角速度趋于恒定值。整流罩为弹性模型时，由于呼吸运动分离角速度变化曲线有较大幅度振动，且分离角速度相对刚体模型明显较小。

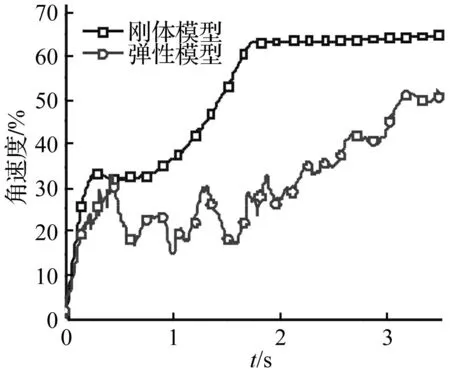
图10　整流罩分离角速度变化曲线 Fig.10 Fairing separation angular velocity

整流罩在过顶、脱钩时刻分离参数仿真结果见表1。由表1看出，刚体模型仿真所得过顶角速度与理论估算结果误差仅2.7%。而由弹性、刚体模型仿真结果对比知，由于呼吸运动造成分离弹簧弹性势能损耗，导致整流罩过顶、脱钩时间明显延后，过顶、脱钩角速度明显较小。为使整流罩在设计要求时间内以足够速度安全分离，在分离系统设计过程中须充分考虑因呼吸运动所致能量损耗。

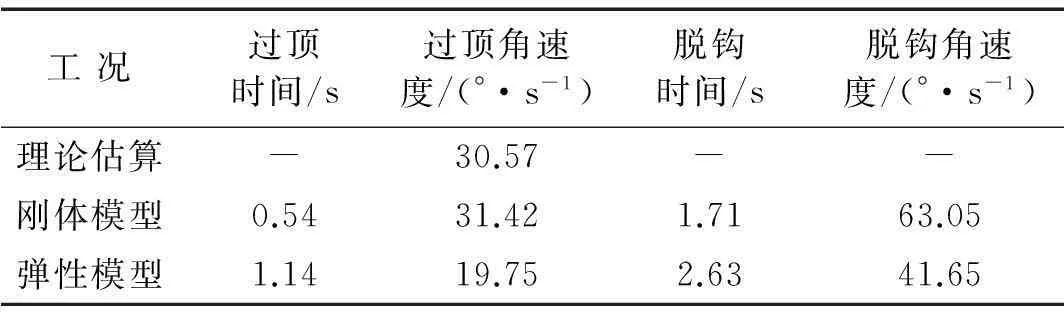
表1　整流罩分离参数仿真结果

2.3呼吸运动对罩内包络空间影响分析

整流罩分离过程中变形特点及Y、Z、径向位移定义见图11。整流罩内可用包络空间可视为分离前的静态包络空间，随分离过程继续，若不考虑呼吸运动，整流罩与有效载荷间距会逐渐增大。考虑呼吸运动时则可能导致距离减小。整流罩静态包络空间为圆柱体，呼吸运动对罩内可用包络空间影响可通过径向位移体现。

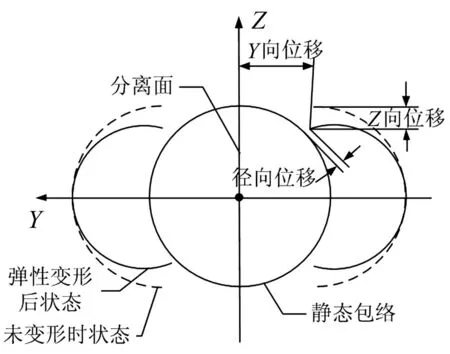
图11　整流罩变形特点示意图 Fig.11 Sketch map of deformative characteristic in fairing

分离过程中整流罩后柱段下端、前柱段与前锥段对接处Y、Z向位移变化曲线见图 12、图 13。由两图看出，整流罩分离后柱段下端在Z轴向罩内移动最大距离51 mm，时间为0.25 s，此时该处Y向位移为32 mm。相对后柱段下端，前柱段与前锥段对接处对罩内可用包络空间影响较小；后柱段下端Z向位移变化趋势与前柱段、前锥段对接处Z向位移变化趋势相反，即后柱段下端Z向位移为正时，前柱段、前锥段对接处Z向位移为负。

整流罩后柱段下端、前柱段与前锥段对接处径向位移变化见图 14。由图14看出，后柱段下端在0.25 s时沿半径向罩内移动51 mm，即整流罩呼吸运动导致后柱段下端罩内可用包络空间在半径上减少51 mm。在0.21 s时前柱段、前锥段对接处沿半径向罩内移动13 mm。曲线在分离初始时振幅较大，随分离过程继续，振幅逐渐减小。

整流罩后柱段下端两点Z向坐标值随Y向坐标值变化曲线见图 15，虚线为整流罩分离前端静态包络。由图15看出，分离前后柱段下端两点间距为5.2 m，分离开始后两点对罩内可用空间造成一定影响。

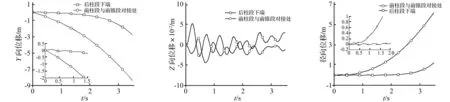
图12 Y向位移变化曲线Fig.12CurvesofYdisplacementchange图13 Z向位移变化曲线Fig.13CurvesofZdisplacementchange图14 径向位移变化曲线Fig.14Curvesofradialdisplacementchange

2.4分离过程中能量变化情况分析

整流罩分离过程中时刻伴随能量转化。用弹性模型计算时，分离过程各能量变化曲线见图 16。由图16看出，分离初始弹簧内储存的势能为11 KJ，并在0.29 s释放完。过载做功在分离初始为0，之后逐渐减小并在1.14 s达最小值。此因整流罩分离中达过顶处时前质心逐渐升高，过载做负功。而达过顶后过载做正功，曲线逐渐升高。整流罩动能随弹簧势能释放逐渐增加，释放完后随过载做负功而减小，达过顶后又随过载做正功而增大。整流罩由于呼吸运动吸收的弹性能(即整流罩弹性能)初始时随弹簧势能释放而增加，之后逐渐稳定在4 KJ左右。因此，整流罩分离过程中弹簧势能未完全转化为整流罩动能，其中36%左右转化为整流罩弹性能。

利用刚体模型计算时，由于不考虑整流罩的呼吸运动，其弹性能恒为0，分离中弹簧势能全部转化为整流罩动能，弹簧势能利用率为100%，见图17。

图15 后柱段下端Y-Z变化曲线Fig.15Y-Zcurvesofendtwopointsforfairing图16 弹性模型分离过程中能量变化曲线Fig.16Energychangeincourseoffairingseparationforflexiblemodel图17 刚体模型分离过程中能量变化曲线Fig.17Energychangeincourseoffairingseparationforrigidmodel

3结论

在考虑整流罩呼吸运动基础上，对大型柔性整流罩分离过程进行仿真分析，获得运动轨迹、姿态、分离角速度、罩内可用包络及能量变化，结论如下：

(1)呼吸运动对罩内可用包络空间影响最大区域为后柱段下端及前柱段与前锥段对接处，损失最严重的在后柱段下端，半径上约51 mm。

(2)整流罩质心各向位移变化曲线未体现振动特点，即呼吸运动对整流罩整体运动轨迹变化影响不明显。

(3)呼吸运动会导致整流罩过顶及脱钩时间延后，并使过顶、脱钩角速度明显减小，并致分离弹簧势能损失约36%。

(4)大型柔性整流罩分离过程精确仿真分析难度较大，影响因素较多且相互耦合，较复杂。尚有大量问题亟待进一步深入研究。

参考文献

[1]李耀民．卫星整流罩设计及“三化”[J]．导弹与航天运载技术,1999(2):1-11.

LI Yao-min．Satellite fairing design and systematization standardization and combination[J]．Missiles and Space Vehicles,1999(2):1-11.

[2]徐永成,苟永杰,王石刚. 某卫星整流罩分离仿真分析[J].上海航天,2009(1):53-56.

XU Yong-cheng, GOU Yong-jie, WANG Shi-gang. Simulation analysis of separation for some satellite fairing[J]．Aerospace Shanghai,2009(1):53-56.

[3]董寻虎,骆剑．大型柔性整流罩抛罩多体动力学仿真[J]．上海航天,2005(5):28-33.

DONG Xun-hu,LUO Jian．Multi-body dynamics simulation of large scale flexible fairing separation[J]．Aerospace Shanghai,2005(5):28-33.

[4]马忠辉．大型弹性整流罩分离特点分析[J]．中国科学E辑:技术科学,2009,39(3):482-489.

MA Zhong-hui．Analysis of large-scale flexible fairing separation[J]．Sci. China：Ser. E：Technology Sci.，2009，39(3):482-489.

[5]Yasunaga Y,Fukushima Y, Nakamura T, et al．Separation jettison test of japanese h-ii rocket satellite fairing[R]．28th Aerospace Sciences Meeting,1990:1-8.

[6]Yasunaga Y, Motoyama C，et al．Development of separation system for H-II rocket satellite fairing[R]．KHI Technical review No.95,1987.

[7]陆佑方. 柔性多体系统动力学[M]. 北京：高等教育出版社,1996.

[8]Kane T R, Ryan R P, Banerjee A K. Dynamics of a cantulaver beam attached to a moving base[J]. J Guidance, Control Dyn, 1987,10(2):139-150.

[9]MSC. Nastran 2004 release guide [M]．MSC. Software，2004.

[10]Michael R，Mark M. MSC/ NASTRAN quick reference guide[M]．The Neal-Schwendler Corporation，2001.

[11]雷勇军,卓曙君,郑荣跃,等．卫星整流罩结构动力特性与分离运动分析[J]．国防科技大学学报,1997,19(4):23-27.

LEI Yong-jun, ZHUO Shu-jun, Zheng Rong-yue, et al. Dynamic characteristic and separation behavior analysis for satellite fairing[J]．Journal of National University of Defense Technology,1997,19(4):23-27.

[12]LS-DYNA keyword user’s manual [M]．Livermore Software Technology Corporation, 2003.