海洋石油平台电缆敷设优化设计软件的开发及应用

黄太安，王 佳，张小钢，邢兰昌，贾明鑫，蒋小华，李玉明

[海洋石油工程(青岛)有限公司，山东 青岛 266520]

海洋石油平台电缆敷设优化设计软件的开发及应用

黄太安，王 佳，张小钢，邢兰昌，贾明鑫，蒋小华，李玉明

[海洋石油工程(青岛)有限公司，山东 青岛 266520]

海洋石油平台建造过程中，电缆敷设路径的精确定位和电缆材料的精确控制一直是一个难点。结合三维模型精确计算出电缆敷设路径及长度，在此基础上实现电缆预裁，无疑是解决该难点的有效方法。电缆敷设优化软件利用电缆路径的节点原理，基于PDMS平台进行二次开发，通过高效算法在关键节点自动进行电缆排布，能够准确计算出电缆长度，有效提高电缆路径敷设效率，节省电缆材料成本。

海洋石油平台；电缆敷设；PDMS；材料控制

0 引 言

随着海洋石油平台日趋大型化、复杂化和智能化，平台上的电力电缆、仪表控制电缆、通信电缆等的种类规格日趋繁多，数量也日趋庞大。而由于海洋石油平台的空间局限性，设备、管道、通风、电气、仪表等专业必须共同使用有限的空间，导致电缆托架的空间布置错综复杂，给电缆敷设工作带来了极大的困难。电缆作为平台的“动脉和神经”，其施工是否符合相关标准规范、满足安全运行要求，直接关系到平台生产、运行、人员及设备的安全。电缆敷设既要满足一定的施工规范，又必须考虑电缆材料的用量，以达到项目的成本目标。面对成千上万根电缆，如何进行路径优化设计[1-2]，毫无疑问是电缆敷设工作的关键点。针对这一问题，本文基于PDMS(Plant Design Management System)平台进行二次开发，通过高效算法在关键节点自动进行电缆排布，利用开发的电缆敷设优化软件，实现海洋石油工程领域电缆的精确设计和施工。

1 软件设计原理

本系统的开发是利用节点原理，结合PDMS二次开发，制定高效准确的电缆敷设路径，其算法考虑节点处的电缆排布，较为准确地计算出电缆使用长度，有效提高电缆路径敷设效率，节省电缆的材料成本。

1.1 优化算法设计

算法不仅要实现寻找电缆敷设路径的最短路径，还要实现重要节点处的电缆排布优化，较为准确地计算出电缆的理论长度和电缆截面圆心的绝对坐标，提高电缆路径定位的准确度。在进行路径和截面优化的同时，还要兼顾填充率、弯曲半径等工艺要求。

1.1.1最短路径的实现

用于解决最短路径问题的算法被称作“最短路径算法”，简称“路径算法”。最常用的路径算法有Dijkstra算法、Bellman-Ford算法、SPFA算法以及DAG 图算法[3]。

Dijkstra算法解决了有向图上带权的单源最短路径问题，时效性好，使用了贪心策略；Bellman-Ford 算法能在一般的情况下(存在负权边的情况下)，解决单源最短路径问题；SPFA 算法是Bellman-Ford 的队列优化，时效性相对好，但SPFA 的算法时间效率是不稳定的，即它对于不同的图所需要的时间有很大的差别；DAG 图算法是有向无回路图计算单源最短路径的算法。

经过比较这四种算法，联系海洋石油平台电缆敷设的实际，本系统采用效率稳定和复杂度适中的Dijkstra算法进行路径优化设计。

Dijkstra算法是典型最短路径算法，在大量的最短路径算法中，Dijkstra算法是一种最经典的方法，很多算法都是在该算法的基础上经过改进发展而来。

Dijkstra算法主要思想为：通过遍历整个图找到每个点的最短路径，从而确定目标点的最短路径。Dijkstra 算法设置了一顶点集合S，从源点s到集合中的顶点的最终最短路径的权值均已确定。算法反复选择具有最短路径估计的顶点u，u∈V-S，并将u加入S中，对u的所有出边进行松驰。

随着网络空间数据的增大，网络节点数的增加，直接使用Dijkstra算法会占用计算机的内存，降低处理效率，而且遍历的节点过多会使算法速度下降。为了处理大数据量的最短路径问题，我们通过避免使用关联矩阵，利用网络拓扑信息中的弧段的连接关系，对Dijkstra算法进行了优化。优化后该算法可以节约大量的内存，对于结点数比较大的网络，或带有大量拐向限制设置的网络，具有较好的适用性[4]。

最短路径将以路径所经过的各个节点的编号的形式给出(编号之间用@分隔)，同时计算出路径的总长度。将优化完成的路径存储待下面使用和进一步优化。

1.1.2处理存在必经点和回避点的路径

首先我们要判断是否存在必经点和回避点。若不存在必经点和回避点，仍使用第一次优化后的最短路径，同时为防止算法出错，赋值存放必经点和回避点的存储空间为“无”。若经判断存在必经点和回避点，则做进一步处理。

存在必经点时，把必经点当作中间点，进行两次路径优化，然后把得到的两段路径相加便得到经过必经点的最短路径。

例如：求点A到点B的最短路径，必经点为H。先求出点A到点H的最短路径：A→C→D→H；再求点H到点B的最短路径：H→L→M→O→B；把两段最短路径相加：A→C→D→H→L→M→O→B，便得到点A到点B且经过点H的最短距离。存在多个必经点采用相同的处理方法。若经过必经点路径无法敷设，则报警输出相应的警告信息。

存在回避点时，处理该路径前把回避点对应的数据信息和连接关系暂时删掉，求出的最短路径就不包含回避点。删掉回避点电缆无法敷设时，报警输出相应的警告信息。

用经过必经点和回避点优化后的最短路径代替之前的最短路径，若有警告信息输出，则沿用之前的最短路径。

1.2 电缆排布优化的实现

当有多根电缆通过同一节点、电缆敷设路径出现拐弯时，为防止电缆出现排布不合理、交叉、缠绕等情况，必须进行电缆排布的优化。

1.2.1排布的规则

(1) 先排粗电缆，后排细电缆。

(2) 先排总体路径长的，后排路径短的。若与(1)冲突，则优先考虑(1)。

(3) 先把底面布满，然后再排到第二层第三层。

(4) 保证电缆的弯曲半径不低于电缆直径的10倍，如果电缆托架的弯曲半径不够，则把这个电缆放在最外侧。

1.2.2截面排布优化

不同电缆在同一节点截面排布的优化是通过对电缆截面圆心绝对坐标的处理来实现的。根据电缆的半径和排放规则，可以计算出各个圆心的绝对坐标，从而得出电缆在该节点的位置。

电缆走向不同，圆心绝对坐标的计算也不同，在计算之前需要判断电缆的走向。根据电缆托架节点的坐标即可判断电缆的走向。

不同走向的两段电缆托架的俯视图如图1所示。A、B、C、D分别为电缆托架底面中心线的起始点，其绝对坐标分别为：A(x1,y1,z1)，B(x2,y2,z2)，C(x3,y3,z3)，D(x4,y4,z4)。空间直角坐标系符合右手螺旋法则。当x1=x2，y1≠y2时，托架方向为y轴正方向，即水平方向。当x3≠x4，y3=y4时，托架方向为x轴正方向，即竖直方向。

1.2.3托架拐弯处的处理

电缆托架俯视图如图2所示，托架拐弯处节点(A点、C点、E点、G点)是由连接拐弯处直托架的底面中心线的交点定义的。例如：拐弯处的节点A，是托架HA和托架AB底面中心线的交点。

图2所示托架的拐弯处共有四种情况。设拐弯处节点(如A点)坐标为(x,y,z)，前一个节点(如H点)坐标为(x0,y0,z0)，后一个节点(如B点)坐标为 (x1,y1,z1)。

当x=x0，y>y0，xy1(逆时针敷设)时，该拐弯为A点处的拐弯。

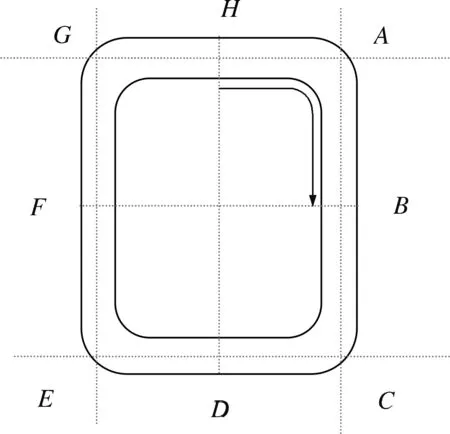
图2 托架拐弯处节点Fig.2 Cable tray corner node

当x>x0，y=y0，x=x1,y>y1(顺时针敷设)，x=x0，y>y0，x>x1,y=y1(逆时针敷设)时，该拐弯为C点处的拐弯。

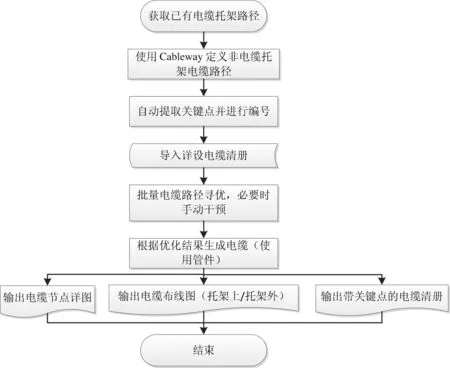
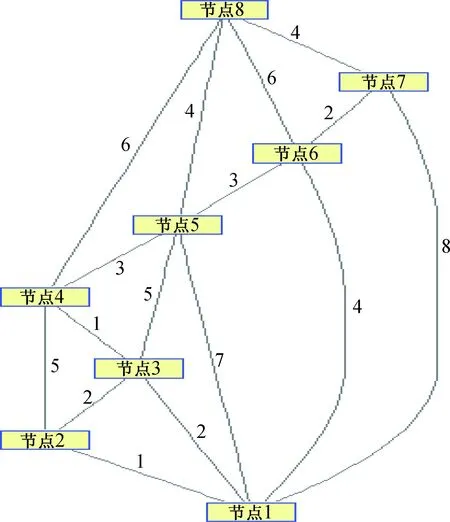
当x=x0，yx1,y=y1(顺时针敷设)，x>x0，y=y0，x=x1,y

当x

针对上述四种不同的拐弯情况，在圆心绝对坐标的计算过程中做相应的处理。

1.2.4填充率优化

在电缆排布的过程中，填充率也是十分重要的因素。在一般情况下，电力电缆的梯架和托盘内的填充率可取40%～50%，控制电缆可取50%～70%，且宜预留10%～25%工程发展余量。在电缆托架的宽度和高度已经确定的情况下，可以通过控制电缆的数量使填充率在规定的范围内。

2 软件功能实现

电缆路径敷设优化设计程序流程如图3所示。

2.1 获取已有电缆路径

采用一种新的电缆布线解决方案，在获取现有电缆托架路径的基础上用实体模型电缆进行布线设计。可以使用程序自动获取已有的电缆托架路径，并用Cableway进行标记。Cableway是PDMS电缆解决方案中自带的电缆占位元素，用于电缆布置占位。Cableway包含5类主要的子元素：HATTA(头)、TATTA(尾)、Route Point(位置定位点)、Route Note(多用途标记点)、Attachment Point(分支接入点)。可以将电缆托架的所有特殊位置点用Route Point点表示出来，包括托架的起止位置、弯头、爬坡、变径等。至于路径宽度、高度、弯曲半径等参数则需在Cableway Branch级进行设置。

首先获取电缆托架路径，包括电缆托架路径和非电缆托架路径。所有电缆可以使用的路径均由Cableway定义完成。本系统直接使用Cableway的Route Point和Attachment Point作为电缆路径关键点。关键点位置信息及关键点之间连接关系如图4和图5所示。

图3 程序流程图Fig.3 Flow chart of program

图4 关键点位置信息Fig.4 Key point location information

图5 关键点之间连接关系Fig.5 Connection relation information of cable route

2.2 导入电缆清册

电缆清册格式如图6所示，其中包含了电缆编号、型号等信息。要进行电缆布线，除了这些信息我们还需要电缆的外径、起止位置的关键点，这些信息需要手动补录入表中。添加缺失属性后的电缆清册如图7所示。

图6 电缆清册Fig.6 Cable list

图7 修改后的电缆清册Fig.7 Cable list revised

导入修改后的电缆清册再加上获取的电缆路径，电缆路径自动优化计算的数据准备就完成了，可以通过优化算法对电缆路径进行优化。

2.3 电缆路径优化

电缆铺设路径优化插件的功能包括：(1)导入所需数据，即电缆清册和电缆路径；(2)自动路径寻优，即电缆路由优化和截面排放优化；(3)人工调整，即专业人员对自动路径寻优结果的适度调整；(4)最优路径导出，即输出最终的电缆敷设路径结果。

以上功能开发通过两个步骤来实现：(1)优化算法的开发与验证，即应用功能强大的数值计算软件MATLAB所提出的优化算法进行程序实现，并通过实例进行算法验证，以确保算法与程序的正确性与稳健性；(2)代码转换与插件开发，即将所开发的MATLAB程序进行代码转换，转换为C程序，可直接用于开发PDMS的插件。

2.3.1信息预处理

以上数据准备已经为电缆路径优化提供了必要的数据信息，即电缆可选择的路径(如电缆托架路径、马脚等)和电缆参数(如编号、型号、外径、起始位置等)；除此之外，作为优化计算约束信息的设计工艺要求(如填充率、弯曲半径等)也已经明确。

下面需要对以上数据信息和约束信息进行数学模型化预处理，即将这些信息转换为优化算法能够识别、处理的模型化数据。基于以上模型化数据，应用MATLAB画出的电缆托架路径图如图8所示。

图8 应用MATLAB画出的Cableway图形Fig.8 Cableway graphics drawn by MATLAB

2.3.2路由优化计算

路由优化计算采用Dijkstra算法。Dijkstra算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

下面通过计算实例说明如何采用Dijkstra算法进行电缆路由优化。假设电缆路径由8个节点互联而成，连接关系如图9所示，每两个节点之间的距离各自定义，可相同也可不同。现在需要铺设电缆将节点1和节点8连接，应用路由优化算法寻找最短的路径，转化为以下模型。

(1) 各路径起始节点： [1,1,1,1,1,2,2,3,3,4,4,5,5,6,6,7]。

(2) 各路径终止节点：[2,3,6,7,5,3,4,4,5,5,8,8,6,7,8,8]。

(3) 各路径权值：[1,2,4,8,7,2,5,1,5,3,6,4,3,2,6,4]。

(4) 寻找节点1到节点8的最优路径。

图9 节点以及路径图Fig.9 Node and route graph

进行路由优化计算，得到连接节点1和节点8最短的路径为：节点1—节点3—节点4—节点8，总长度为9。计算结果如图10所示。

图10 最优路径图Fig.10 Optimalized route graph

2.3.3截面排放优化计算

以上路由优化计算的结果为电缆截面排放优化计算提供了初步的电缆路径信息。在获取了初步的电缆路由优化计算结果后，首先根据工艺设计要求对结果进行检验并给出是否符合工艺要求的判断结果。如果在某一(或某些)方面违反了工艺要求，则需要重新进行路由优化计算；如果完全符合工艺要求，则进行截面排放优化计算。

电缆截面排放优化计算过程充分考虑以下设计要求，如果存在某些设计要求相互抵触，则优先满足填充率、电缆弯曲半径、强弱电缆类型等要求。

(1) 仪表电缆的相关加工设计，主要参照《工程建设标准强制性条文 (石油和化工建设工程部分)》。在加工设计时，相关内容主要体现在电缆滚筒清册、仪表安装程序和电缆护管的布置和加工设计图中。

(2) 当几种电缆托架垂直分层安装时，应按如下顺序设计：仪表信号线路、安全连锁线路、仪表用交流和直流供电线路及电气托架。

(3) 托架拐直角弯时，其最小的弯曲半径不应小于托架内最粗电缆外径的10倍。

(4) 本质安全型仪表的信号线和非本质安全型仪表的信号线应加以分隔。当仪表有特殊要求时，应按仪表安装使用说明书的规定进行配线。

(5) 电缆托架的宽度应根据所布电缆的数量确定，一般填充率不超过托架容量的60%。

电缆截面排放优化计算方法主要采用智能搜索算法：第一，将各种设计要求进行优先级排序并数值化，对现有的电缆路由计算结果进行逐一检验以及总体检验，评价目前路由对设计工艺条件的适用度；第二，适用度为100%即为完全符合设计工艺要求，若小于100%则需根据相应的不适用指标的优先级进行截面排布调整，若截面排布调整后仍不能使得适用度达到100%，则需进行附加约束条件的路由优化，然后再次进行截面排布优化；第三，如果经过以上步骤仍不能实现适用度为100%，则需要进行人工调整。

2.3.4人工调整

为了进一步保证路径优化结果的准确性、合理性和实用性，需要专业人员重新审视路径优化结果，在发现适用度达不到100%的情况下对优化结果进行权衡和处理，如优先保证哪个指标等，在此基础上对优化结果进行手动调整，调整的内容包括两方面，即路由调整和截面排放调整。

2.4 软件系统功能模块

电缆路径敷设优化功能最终由一个PDMS插件来实现。插件页面如图11所示。具体步骤如图12～14所示。

图11 PMDS插件界面Fig.11 Interface of PMDS plug-in

图12 应用Cableway编号系统对电缆路径进行编号Fig.12 Number cable route using Cableway numbering system

图13 应用自动布缆系统导入电缆清册Fig.13 Import cable list using automatic cabling system

图14 应用自动布缆系统导出包含最优电缆路径的数据文件Fig.14 Export the data file containing the optimized cable path using the automatic cable distribution system

3 结 语

本文对利用电缆路径节点原理、结合PDMS二次开发的电缆敷设优化设计软件的设计原理以及功能实现进行了详细论述。该软件系统利用“最短路径算法”并充分考虑工艺要求，对电缆敷设路径进行优化设计，不仅可以准确地计算出电缆的使用长度，还能提取关键节点处的电缆空间排布图，为海洋石油平台电缆预裁提供了数据基础，能够有效提高电缆路径定位效率，节省电缆材料成本。该方案填补了国内海洋石油工程领域的空白，为电缆的精确设计和施工提供了可行的方法。

[1] 张鹏．基于遗传算法的船舶电缆布置优化设计的研究 [D]．大连：大连理工大学，2014.

[2] 林伟波．敷设软件在核电厂路径设计中的应用及深化 [J]．中国科技信息,2013(20):74.

[3] 郑海虹. 常用最短路径算法分析与比较[J]．安徽电子信息职业技术学院学报,2013(4):31.

[4] 张福浩, 刘纪平，李青元. 基于Dijkstra算法的一种最短路径优化算法[J] ．遥感信息，2004(2):38.

DevelopmentandApplicationofCableLayingRouteOptimizationSoftwareinOffshoreOilPlatform

HUANG Tai-an， WANG Jia， ZHANG Xiao-gang， XING Lan-chang， JIA Ming-xin， JIANG Xiao-hua， LI Yu-ming

[OffshorePetroleumEngineering(Qingdao)Co.,Ltd.,Qingdao,Shandong266520,China]

In the construction of offshore oil platform, the precise positioning of cable laying route and material control is always a big challenge. To slove this problem, we can realize the cable precut on the basis of accurate calculation of cable laying route and construction length in three-dimensional (3D) model. By making secondary development based on the principle of the nodes of the cable path and PDMS, we develop the cable laying route optimization software. It uses the efficient algorithm at key nodes to make automatic cable layout, so that we can accurately calculate the cable length, effectively improve the cable route laying efficiency and save the cable material cost.

offshore oil platform； cable layout; PDMS； material control

2016-04-07

黄太安(1982—)，男，高级工程师，主要从事海洋石油工程三维设计方面的研究。

TE541;TP319

A

2095-7297(2016)05-0323-08