无线传感器/反应器网络中反应节点优化重定位机制研究

无线传感器/反应器网络中反应节点优化重定位机制研究*

赵新元

(新疆师范大学网络信息安全与舆情分析实验室，新疆 乌鲁木齐 830054)

摘要：针对无线传感器/反应器网络中因多个反应器失效而造成的反应器网络连通性被破坏问题，以网络流理论为基础，提出了一个基于网络流的多目标规划模型来求解优化的反应器重定位方案。模型将反应器网络看成是一个运输网络，通过流平衡条件来重建反应器网络的连通性。最小化多个参与恢复的反应器总体开销和最小化单个反应器的最大开销是该模型的两个优化目标。仿真实验结果表明，基于该模型的优化重定位方案能够有效地恢复因多反应器节点失效而造成的网络连通性问题。

关键词：多反应器失效;连通性恢复;网络流；优化重定位开销

中图分类号：TP393 文献标志码：A

doi:10.3969/j.issn.1007-130X.2015.06.011

收稿日期：*2014-04-08;修回日期：2014-08-14

作者简介:

通信地址：830054 新疆乌鲁木齐市新医路104号新疆师范大学网络信息安全与舆情分析实验室

Address:Laboratory for Network Information Security and Public Opinion Analysis,Xinjiang Normal University,104 Xinyi Rd,Urumqi 830054,Xinjiang,P.R.China

Research on optimal actors’relocation in wireless sensor and actor networks

ZHAO Xin-yuan

(Laboratory for Network Information Security and Public Opinion Analysis,

Xinjiang Normal University,Urumqi 830054,China)

Abstract:The connectivity of actor networks is vital in the wireless sensor and actor networks (WSANs) due to the nature of the WSANs operation. Relocating actors is an effective solution to restore the connectivity when actors fail.The relocation solutions proposed in recent studies do not optimize the relocation distance. In this paper we present a network flow based multi-objects actor relocation model to handle multiple actors' failures. Minimizing the total overheads and the individual maximal overhead are the two optimal objectives.To restore the connectivity of the network, the model constructs a flow balancing condition for the actor network which can be treated as a transportation network.The simulation results demonstrate the effectiveness of the proposed model and show that the model outperforms other existing approaches in terms of optimal restoration overheads in handling multiple failures.

Key words:multiple actors failure;connectivity restoration;net flow;optimal relocation overheads

1引言

无线传感器/反应器网络WSANs(Wireless Sensor and Actor Networks)是无线传输器网络WSNs(Wireless Sensor and Networks)的一个变种，其中部署了两种重叠的网络，一种是由可以移动的反应器(Actor)构成的反应器网络，另一种就是由传感器节点组成的传感器网络[1]。相对传感器来说，反应器节点的资源受限程度较小，具有较大的能量、传输距离以及处理能力等等。反应器节点从传感器节点收集数据，通过与WSANs中的其他反应器节点的相互协作来完成任务,这是WSANs网络的一个重要特性[2]。因此，维护反应器网络的连通性就变得尤为重要了。

反应器节点的失效会造成反应器网络连通性的破坏。尽管单个反应器失效的概率要远远高于多个反应器节点，但研究多反应器同时失效也是非常有意义的。例如，在战场环境中，一次爆炸可能会导致一个区域内多个反应器节点失效，或者是在安全应用方面，一次有敌意的攻击可能会使WSANs网络中多个反应器节点同时失效。通过重定位剩余的反应器节点来重建反应器网络是一个可行的办法。在这种情况下，主要考虑的是以尽可能小的重定位开销来恢复网络的连通性。

本文提出一个基于网络流的多目标优化反应器重定位模型NAOM(Network flow-based multi-object Actor Relocation Model)来恢复反应器网络的连通性。模型的第一个优化目标是最小化重定位过程中所有反应节点的总体开销。一般来说，反应器节点移动能耗要远大于其通信能耗，因此本文只考虑节点移动引起的开销，即重定位距离(本文中开销与重定位距离是同义语)。只优化总体开销有可能导致单个反应节点的开销过大，从而影响了反应节点的生存期，所以模型的第二个优化目标是最小化个体的最大开销，即单个反应器节点的最大移动距离。本文以网络流理论为基础，首先将反应器网络看成一个运输网络，然后利用流平衡条件来重建网络的连通性。该问题被建模为一个二次混合整型数学规划模型。

2相关研究

近年来已有很多文献关注恢复因单点失效而造成的WSANs网络中反应器网络连通性被破坏的问题[3]。 Abbasi A A等人[4]针对WSANs网络提出一种典型的基于关键点(即失效节点为反应器网络拓扑中的割点)的分布式解决方案DARA。DARA利用2跳邻居表和级联移动机制有效地恢复了断开的反应器网络。Younis M等人[5]则针对WSNs网络提出了另一种不依赖于关键点的典型的分布式算法RIM来修复断裂的网络。RIM的主要思想是让失效节点的邻居向着失效节点移动，直到它们之间建立连接为止，这个过程被递归应用到后续的节点移动中。与DARA算法相比，RIM产生的个体开销要小于DARA，但其产生的总体开销要远远大于DARA产生的总体开销。文献[6～10]分别从不同的方面对RIM和DARA算法进行了改进。但是，这些分布式算法均只能处理单一节点失效问题。

恢复因多节点失效而造成的网络连通性问题要比单节点失效困难一些。刘林峰等人[11]提出了针对WSNs网络中多传感器节点失效时恢复WSNs网络拓扑自愈算法。该算法在发现节点失效后通过调整一些未失效节点的功率来完成拓扑的自愈。Lee S等人[12～14]则利用Steiner树来研究向WSNs网络中部署最少的后备节点来重建网络的连通性，这实际上是一个NP-难问题[15]。但是，由于反应器的代价比较大，因此利用在反应器网络中部署冗余的反应器节点以防止节点故障不太适合于WSANs网络。Akkaya K等人[16]针对WSANs中反应器网络最早提出了侦测断裂子网的分布式发现算法和子网融合算法。该方法利用WSANs网络中的传感器作为中继节点，采用基于行-列广播机制来侦测断裂的反应器网络，然后在子网中选出一个首领反应器节点，多个子网的首领反应器通过基于最小连接集的移动机制将断开的反应器网络融合在一起。Alfadhly A等人[17]则提出了一种基于树的恢复机制来处理多节点失效时网络的连通性问题。算法预先在网络中构造一棵树，当失效发生时，失效反应器的孩子节点通过彼此之间的协作来触发重定位机制。Mi Zhen-qiang等人[18]则研究了移动Adhoc网络中的多节点失效问题，介绍了一种基于K跳邻居信息的分布式机制来恢复节点之间的连接性。但是，以上的分布式恢复机制仅关注于恢复网络连通性而忽略了对恢复开销的优化。

Alfadhly A等人[19]首先提出了基于关键点的集中式优化算法ILP。文献[19]将节点重定位问题建模为一个整型线性规划。该算法的目标是求解总体开销最小的节点重定位方案。ILP算法通过将剩余的反应器重新部署在失效的关键节点的位置上来恢复网络的连通性，因此该算法只能处理多个关键点失效的问题。

3处理多节点失效的NAOM模型

3.1简介

在WSANs网络中维护反应器网络的连通性十分重要。反应器节点的失效有可能导致反应器网络的连通性被破坏。在单一反应器节点失效的情况下，只有那些在网络拓扑中位于关键位置上(即反应器网络拓扑中的割点)的反应器失效才会导致网络的连通性被破坏，本文将处于这种位置上的反应器节点简称为关键节点。然而，在多节点失效的情况下，多个非关键节点的失效也可以导致网络连通性的破坏。如图1a中的a8和a9两个非关键节点的失效割裂了整个反应器网络。文献[19]提出的ILP方法无法处理这种情况。为了弥补文献[19]所提出的ILP模型的缺点，本文根据网络流理论提出了一个新的多目标优化模型，来处理网络中因多反应器节点失效而造成的网络连通性恢复问题。

3.2问题描述

本文所提出的问题可以形式化描述为：考虑平面上的一个连通图，图中的每条边长度小于或等于一个预定义的值R。令集合L={li|i=1,2,…,NL}中的每个元素表示连图图中各个顶点的位置。现将反应器信合A={ai|i=1,2,…,NA}中的所有反应器节点放置在连通图的NL个顶点上(NL≥NA)，并假设反应器之间的最大通信距离为R。则该问题实际上就是在位置集合L中重新定位这NA个反应器，使它们能够以最小的总体开销和最小的个体最大开销来建立一个互连的反应器网络。很明显，这个问题是一个典型的多目标优化问题。

3.3基于网络流的优化模型

针对3.2节中提出的问题，可以将连通图看成是一个运输网络，该运输网络中每个位置都是一个运输站(在以下的描述中，站点与位置是同义语)。假定该运输网络可以从一个运输站向另一个运输站运输货物。有如下规定：(1)若运输站拥有反应器节点(即反应器位于该运输站)，则该站能够接收或发出货物；(2)反之，则该站既不能接收货物也不能发送货物。

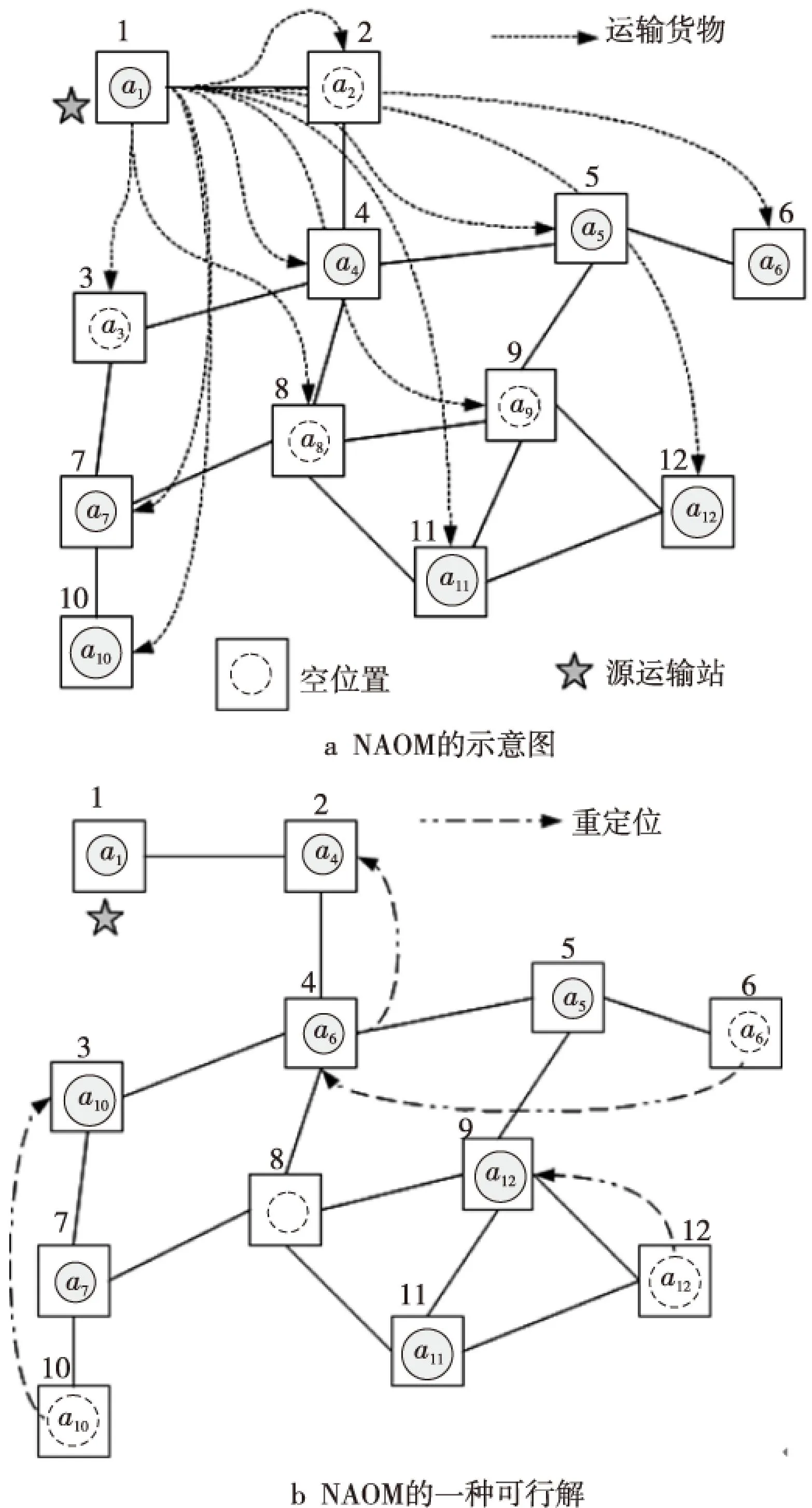
Figure 1　Overview of NAOM 图1　NAOM模型的基本思想

在这个运输网络中，任意选择一个位置作为源站点，由该站点向运输网络中的所有其他站点均发送一个单位的货物。拥有反应器的站点收到不是给自己的货物后必须要转运该货物。最终，若反应器所构成的网络是连通的，则每个拥有反应器的站点必然会收到一个源站点发给自己的货物，否则就表明反应器网络一定不是连通的。图1展示了模型的基本思想。

定义如下描述：

(1)L是平面上包含NL个位置的集合。

(2)A是包含Na个反应器的节点集合，集合中的每个反应器均位于集合L中的某些位置上。

(3)dij表示L中位置i和j之间的距离。

(4)Adij是一个二元值，表示两个位置i、j是否是相邻的。当dij≤R时，Adij=1,其中R是反应器节点之间的最大通信距离。

(5)Xiu是二元值，为1表示反应器u占据位置i。

(6)Oi是二元值，为1表示位置i被一个反应器所占据。

(7)fij表示由站点i发送给站点j的货物的数量。则在集合L中优化重定位集合A中节点可以写成如下的数学规划：

问题：在NL个位置中优化重定位NA个反应器。

已知：L，A,dij,Adij；

求：Xiu,fij,Oi。

(1)

(2)

使得：

(3)

(4)

(5)

(6)

(7)

(8)

(9)

该模型是一个混合整型的二次规划。目标函数(1)和(2)最小化总的重定位距离和最小化单个最大重定位距离。限制条件(3)确保了反应器u必须要重定位到集合L中的一个位置上去，而限制条件(4)则确保L中的任何一个位置i只能够被至多一个反应器所占据。公式(5)表明位置i是否被一个反应器所占据。限制条件(6)则保证源站点s发出的货物总数为NL-1个。等式(7)是一个网络流平衡限制条件，它保证流向站点位置i的总货物量等于1(源站s送至位置i的货物)加上站点i转运的货物数量。该式同时表明，站点j如果拥有反应器则会至少收到一个货物(即Oj=1)。流平衡条件能够保证反应器节点在重定位之后整个反应器网络是连通的。限制条件(8)则限制了站点i向站点j运送的最大货物运输量。根据前面的假定，未拥有反应器节点的运输站既不能接收货物也不能转运货物，因此若位置i或j未被反应器占据，则有fij=0。限制条件(9)表示货物总数量fij为正值。

一般来说，最小化总体开销和最小化个体的最大开销是一对矛盾的优化目标。为了求解这个多目标优化问题，重定义如下优化函数：

(10)

其中α(α∈[0,1])在模型中是一个针对总重定位距离的优化权重值，它表示求解模型时优先考虑优化总体开销的程度。α=0表示该模型在求解时只考虑优化个体的最大开销。在这种情况下，单个反应器节点的开销是最小的，但有可能导致总体开销最大。权重值α=1则表示模型在求解时只考虑优化总体开销而不考虑优化个体开销，因而导致单个反应器节点要花费更多的能量来进行重定位。图1b是图1a中节点a2、a3、a8及a9失效后的一种可行解(可能不是优化解)。

4仿真实验及评价

4.1仿真实验设置及评价参数

为了能够评价优化求解模型NAOM，本文采用AMPL语言[20]来描述该模型并通过IBM LOG CMPLEX 12.04[21]工具箱进行求解。仿真实验中的反应器网络拓扑是在1 000*1 000 m2的范围内随机生成，反应器节点的数目在20到100之间。反应器之间的最大通信半径设置为50 m。仿真实验在不同的网络拓扑中重复30次，最终的优化结果取这30次的平均值。下面为评价模型性能的主要指标：

(1)总体开销TO。该值可以用来描述所有反应器节点在重定位过程中的总体开销，即总体重定位距离。TO可以用来评价整个网络在恢复过程中的能耗情况。最小化TO是模型NAOM的优化目标之一。

(2)个体最大开销MIO和平均开销SIO。MIO越大就意味着个体的能耗越大，因此最小化该值是模型NAOM的另一个优化目标。除了个体最大开销MIO以外，反应器节点的平均开销(平均重定位距离)SIO也可以粗略地评价节点在恢复过程中的个体能耗。在某种程度上它反映了节点的平均性能。

(3)参与重定位反应器节点总数TNA。可以用该值来粗略地评价总体恢复开销在反应器节点上的分布性以及评价网络中受影响的范围。一般来说，TNA越大，网络中受影响的区域就越大。

4.2比对协议及设置

在仿真实验中将NAOM模型、ILP模型[19]和一个典型的分布式算法DARA[6]作对比来综合评价NAOM模型的性能。如表1所示，根据这三个协议各自的适应范围共设置了三个对比实验。实验1用来评价在单点故障的情况下NAOM、ILP和DARA的性能。在30个不同的网络拓扑中，网络中的所有关键节点轮流充当失效节点，仿真结果取它们的平均值。实验2用来评价在多关键点故障情况下NAOM与ILP的性能(因为ILP只能处理多个关键节点失效的情况)。实验3则通过对比在不同的优化权值α下NAOM的性能，α表示在求解NAOM问题(10)时优先考虑优化TO的程度。α=0和α=1分别表示求解NAOM问题时只优化总体开销TO和个体最大开销MIO。实验3随机选择30%的反应器节点同时失效。为了评价NAOM模型在非关键节点失效时的性能，实验3要求随机选择的失效节点中至少要包含多个非关键节点，同时这些非关键节点的失效必须造成反应器网络的断裂。

Table 1　Scenarios for simulation experiments

4.3实验结果

4.3.1单关键点失效

图2展示了实验1的仿真结果。为了描述上简单起见，本文用NAOMα来表明求解NAOM模型时采用的α值。在仿真中，NAOM1.0、NAOM0.0和NAOM0.5分别表示只优化TO、MIO以及均衡优化TO和MIO。从直觉上来说，分布式算法的DARA似乎应该比优化算法ILP和NAOM消耗更多的总开销TO。图2a表示，DARA消耗的TO大于ILP、NAOM0.5和NAOM1.0的TO(图2中ILP、NAOM0.5,1.0的TO曲线是重合的)，但却远小于NAOM0.0的。由于NAOM0.0仅优化求解MIO，因此在该优化方案下会使更多的反应器参与了，移动从而导致了较大的TO，如图2a和图3所示。同时，从NAOM1.0和ILP的TO仿真结果上可以看出二者基本上是相等的，这是因为二者在求解时均只优化TO。从求解NAOM时的优化权值上来说，NAOM0.5似乎应该比NAOM1.0要产生更多的TO，这是因为NAOM0.5在求解时要同时考虑均衡的优化TO和MIO而NAOM1.0只优化TO。然而仿真结果表明NAOM0.5和NAOM1.0的总开销TO基本上是一致的。主要原因在于实验1中只有一个反应器失效并且剩余的反应器只在一些固定的位置上进行重定位。另外，从图2a也可以看到，除了NAOM0.0，算法ILP和算法NAOM要比DARA在总开销TO方面提升大约15%的性能。

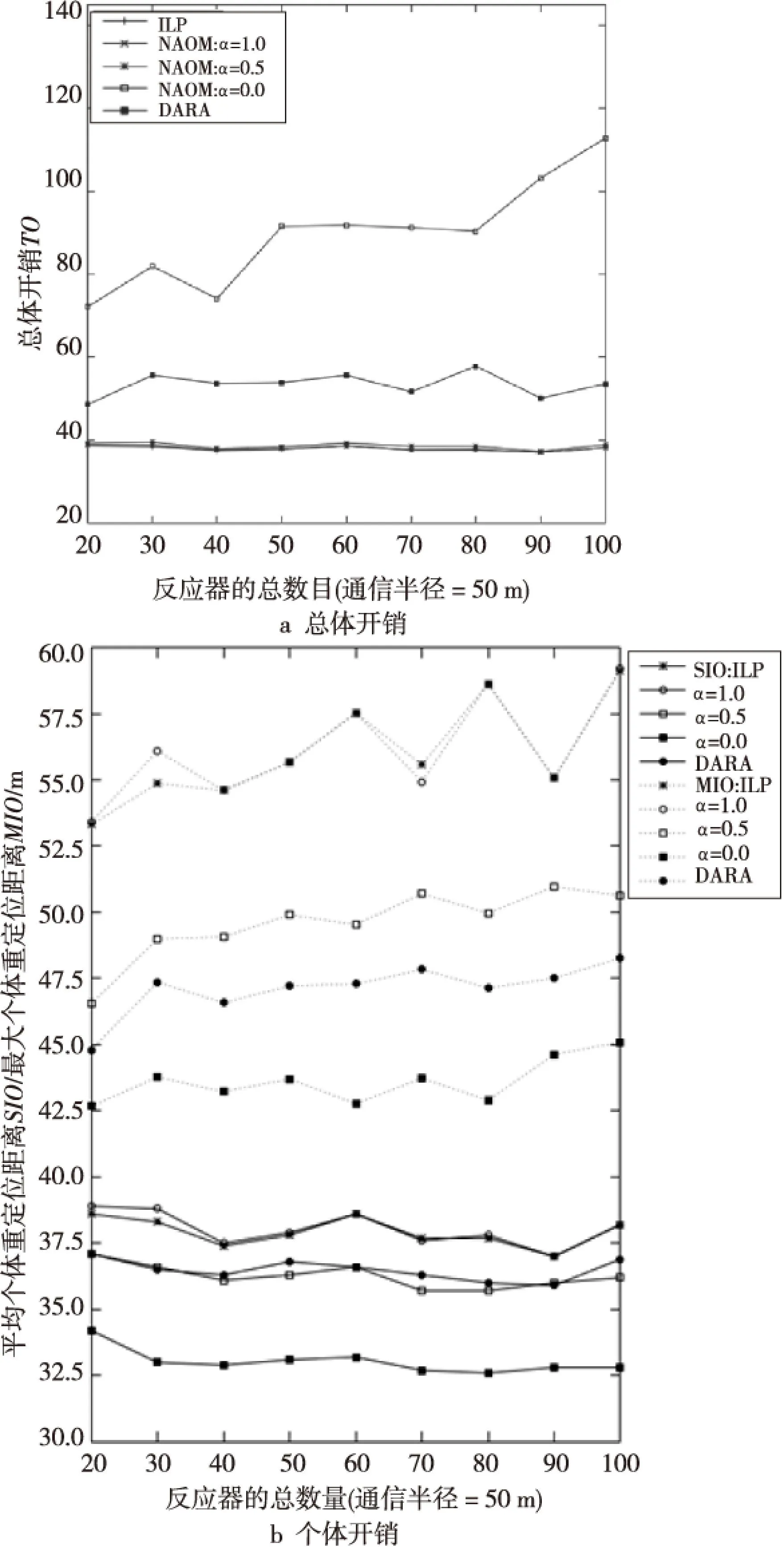
Figure 2　Simulation results for single actor failures(Scenario 1) 图2　实验1的仿真结果

图2b展示了单个反应器的开销情况。正如预料的一样，只优化TO的ILP和NAOM1.0的优化重定位方案使得单个反应器的最大开销MIO和平均开销SIO均比较大。与之相反，NAOM0.0获得了最好的个体性能，但却导致了更多的反应器参与了重定位(如图3a所示)。由于采用级联移动机制，DARA所带来的MIO总是小于节点通信半径。从图中也可以看到NAOM0.5在MIO和SIO方面与DARA基本上是一致的。综合考虑总体开销和个体开销，有理由认为NAOM0.0的部署方案的性能是最差的，尽管该方案下个体的开销最小(比其他的低大约10%)，但却比其它方案消耗了约2～3倍的总体开销。DARA和NAOM0.5比其他方案的性能要好一些。由于DARA是分布式算法而NAOM是集中式算法，因此可以认为DARA的总体性能要优于NAOM0.5，尽管DARA的总体开销要比后者高大约15%。总的来说，实验1的仿真结果表明，在处理单关键点故障方面， DARA的总体性能要优于ILP和NAOM。

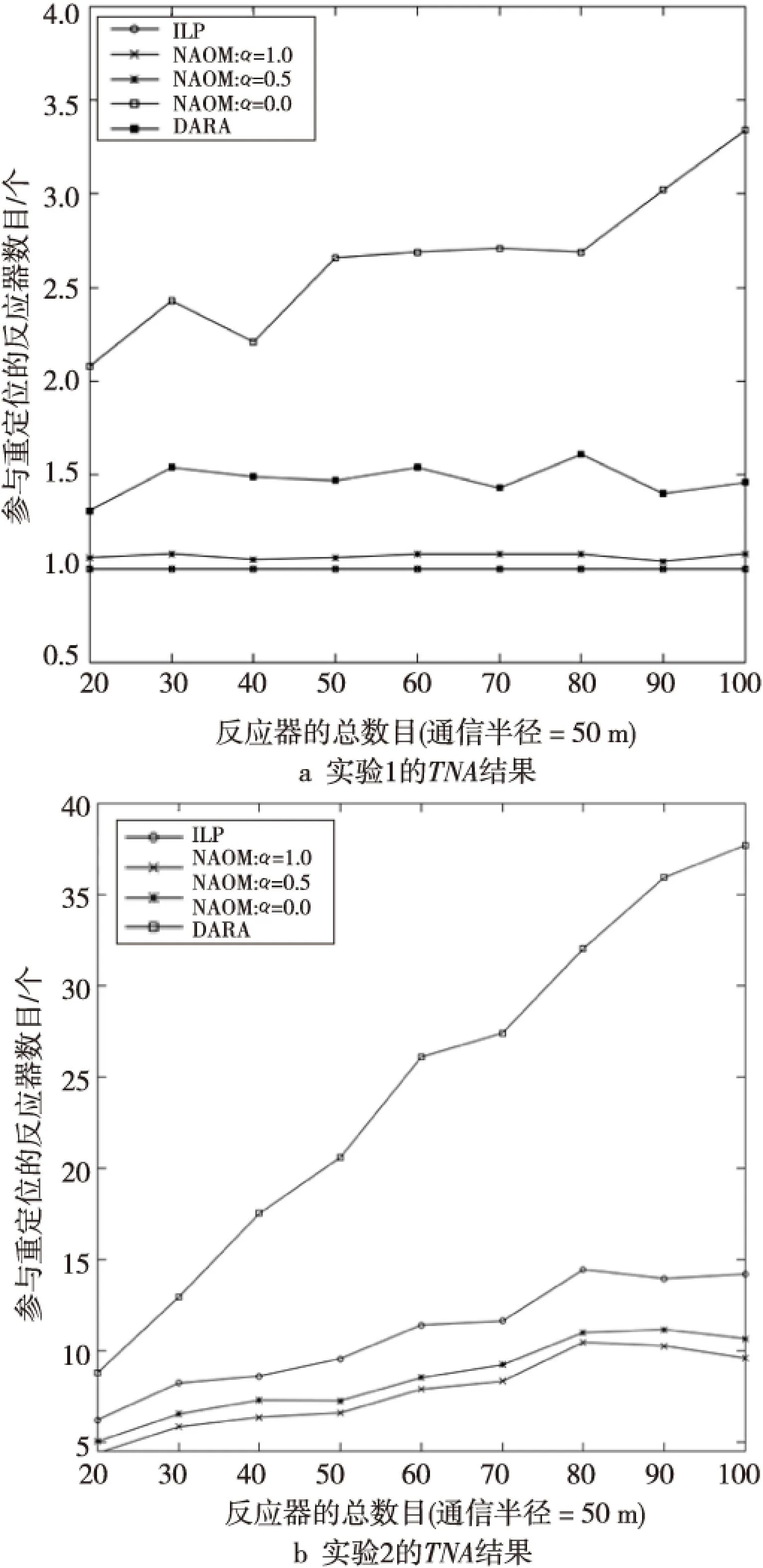
Figure 3　Number of relocated actors in scenario 1 and 2 图3　实验1和实验2中参与重定位的节点数

4.3.2多关键点失效

实验2的仿真结果如图3b和图4所示。图4a表明，随着反应器节点数的增大，ILP和NAOM的总体开销均有所增大。特别是NAOM0.0，由于它仅优化个体开销MIO，因此当节点数比较多时导致的总体开销TO将非常大。这就表明采用NAOM0.0的优化方案会使更多的反应器参与重定位，从图5中可以看到大约有40%～50%的节点均参与了重定位。从图4中还可以看到，尽管ILP和NAOM1.0均是只优化TO，但ILP的总开销TO要大于NAOM1.0的。这主要是因为ILP模型只是通过将剩余的反应器重定位到已失效的关键节点位置上来恢复网络的连通性，而NAOM则利用网络流理论来恢复连通性，在这种情况下并不是所有的失效节点的位置都要被剩余的反应器来占据。如图1a，位置7是运输网络中的关键位置，当节点a7、a8和a9失效后网络被分裂了。将a10重定位到位置8是NAOM模型的一个可行解，尽管在原来的关键位置7上没有反应器。因而NAOM1.0的总开销TO要小于ILP的。

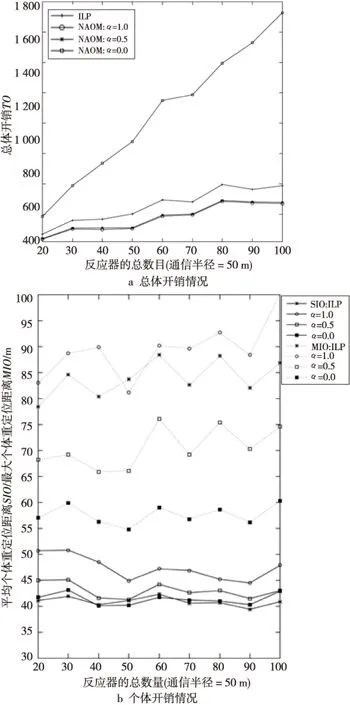
Figure 4　Simulation results for multiple cut-vertices failure(Scenario 2) 图4　实验2的仿真结果

Figure 5　Simulation resubts for multiple actors failure(Scenario 3) 图5　实验3的仿真结果

图4b则展示了模型ILP和NAOM中单个反应器的最大开销MIO和平均开销SIO。正如期望的一样，NAOM0.0的个体性能最优。从图4b中可以看到，ILP和NAOM1.0的最大个体开销MIO基本是一致的，但模型ILP的个体平均开销SIO要小于NAOM1.0的。这种差异是由两种模型ILP和NAOM在重建网络连通性时所采用的不同机制引起的。相对NOAM模型来说，ILP模型使更多的节点参与到重定位过程中(如图5所示)，因此它的SIO要较NAOM1.0的小一些。同时，从图4b中也可以观察到NAOM0.5和NAOM0.0的个体平均开销SIO几乎一样，而且前者的MIO也只比后者的高约13%左右。这说明从个体开销性能上来说，NAOM0.5与NAOM0.0基本是相同的。综合考虑总体性能和个体性能，可以认为在处理多关键节点失效问题方面，NAOM0.5的优化方案要优于ILP和其它的NAOMα(α≠0.5)的优化方案。

4.3.3任意多点失效

图5展示了实验3的仿真结果。实验3仿真了在不同的优化权值α(α=0,0.2,0.5,0.7和1.0)下NAOM模型的优化重定位方案。与实验2类似，NAOM0.0的总体开销TO随着节点数N的增大呈急剧上升的趋势。从图5中也可以看到，当权值α≥0.2时，NAOM所产生的优化重定位方案的总体性能几乎是相等的。这就说明，在求解NAOM模型时仅优化个体开销时如果能够稍微考虑优化一点总体开销，会使优化方案的总体开销大大降低，同时也不会产生太大的个体开销。图5b表明，随着α的增大，NAOM的最大个体开销MIO逐渐趋向于最优值。一般来说，NAOM模型提升个体性能是以牺牲总体性能为代价的。从图5b的仿真结果中可以看到，这些不同α值的NAOM分布方案所产生的MIO最大的差值大约是40 m，而平均开销SIO仅为13 m。这就表明，在求解NAOM模型时仅仅考虑优化个体开销是不可取得，因为它只提升了个体性能大约20%，但却降低了大约300%的总体开销性能。

在仿真实验中，本文也研究了对不同α值来求解NAOM模型所需要的时间。图6展示了α与求解时间的仿真结果。从图6中可以观察到求解时间t反比于优化权值α。也就是说，α越大，求解所需要的时间就越多，这说明求解优化个体开销MIO所需要的时间要大于求解优化总体开销TO。同时，从图6中也发现，求解时间t并不是随着α的增大而均匀下降，这里存在着一个拐点α=0.5。当α≥0.5时，求解时间t与其最小值(即NAOM1.0时的求解时间)的差距变化就逐渐减小了。综合以上三个实验的仿真结果，对于多节点失效问题的处理上可以认为，NAOM0.5所产生的优化重定位方案无论在总体性能还是个体性能方面都要比ILP和其它权值的NAOM方案要好。

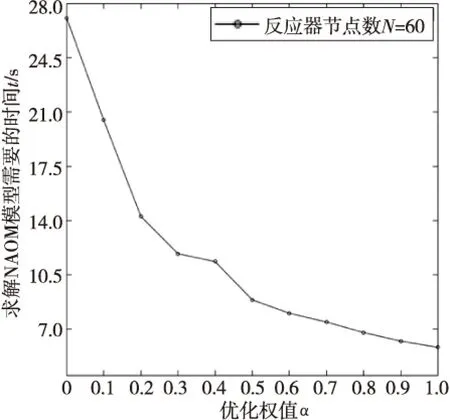
Figure 6　Elapsed time for solving NAOM 图6　求解NAOM的时间

5结束语

本文针对WSANs网络中因多个反应器节点失效而造成的反应器网络连通性断裂的问题提出了一个多目标优化模型来恢复其连通性。通用引入网络流理论将该问题建模为一个二次混合整型线性规划问题NAOM。所提出的模型同时考虑优化总体开销和优化个体的最大开销。仿真结果表明，在处理单关键节点失效问题方面，ILP和NAOM模型的性能与分布式算法DARA的性能基本上是相同的，这就说明在这种情况下用DARA算法来处理单节点失效问题要更好一些。在处理多节点失效问题方面，仿真结果表明仅考虑优化个体开销是一个不明智的选择，因为这会导致总体性能的急剧下降，同时也消耗了更多的模型求解时间。从仿真结果看，对本文提出的模型NAOM来说，均衡地考虑优化总体开销和优化最大个体开销是一个比较理想的选择(NAOM0.5)。同时，NAOM0.5无论是总体性能还是个体性能均要优于ILP模型。NAOM模型的优化求解值也可以作为其他分布式算法的一个评价标准。本文下一步的工作是研究分布算法来处理多反应器失效时反应器网络的连通性问题。

参考文献:

[1]Zhao Wen-dong,Peng Lai-xian,Tian Chang.Survey of coordination mechanisms in wireless sensor and actor network[J]. Journal of Computer Applications,2009,29(8):2183-2187.(in Chinese)

[2]Yang Jie,Feng Yong. Survey on cooperative communication research in wireless sensor and actuator networks[J]. Application Research of Computers,2014,31(3),645-650.(in Chinese)

[3]Kashi S,Sharifi M. Connectivity weakness impacts on coordination in wireless sensor and actor networks[J].IEEE Communications Surveys & Tutorials,2013,2(1):145-166.

[4]Abbasi A A,Younis M,Akkaya K. Movement-assisted connectivity restoration in wireless sensor and actor networks[J].IEEE Transactions on Parallel and Distributed Systems,2009,20(9):1366-1379.

[5]Younis M,Sookyoung L,Abbasi A A.A localized algorithm for restoring internode connectivity in networks of moveable sensors[J].IEEE Transactions on Computers,2010,59(12):1669-1682.

[6]Zhao Xin-yuan,Wang Neng. Overlap-based connectivity restoration approach for wireless sensor and actor network[J]. Journal of Computer Applications,2011,31(10):2638-2643.(in Chinese)

[7]Zhao Xin-yuan,Wang Neng.Coordination-assisted connectivity recovery approach in WSANs[C]//Proc of the 3rd International Conference on Computer Research and Development (ICCRD),2011:82-86.

[8]Imran M,Younis M,Md Said A,et al. Localized motion based connectivity restoration algorithms for wireless sensor and actor networks[J].Journal of Network and Computer Applications,2012,35(2):844-856.

[9]Noman H,Muhammad I.Resource efficient connectivity restoration algorithm for mobile sensoractor networks[J].EURASIP Journal on Wireless Communications and Networking,2012,347(1):1-16.

[10]Abbasi A A,Baroudi U,Younis M,et al.C2am:An algorithm for application-aware movement-assisted recovery in wireless sensor and actor networks[C]//Proc of the 2009 International Conference on Wireless Communications and Mobile Computing:Connecting the World Wirelessly(ACM),2009:655-659.

[11]Liu Lin-feng,Wu Jia-gao,Zou Zhi-qiang,et al. Topology self-cure algorithm aiming at node failure problem in wireless sensor networks[J]. Journal of Southeast University(Natural Science Edition),2009，39(4):695-699.(in Chinese)

[12]Lee S,Younis M. Optimized relay node placement for connecting disjoint wireless sensor networks[J].Computer Networks,2012,56(12):2788-2803.

[13]Lee S,Younis M.Recovery from multiple simultaneous failures in wireless sensor networks using minimum steiner tree[J].Journal of Parallel and Distributed Computing,2010,70(5):525-536.

[14]Lee S,Younis M.Optimized relay placement to federate segments in wireless sensor networks[J].IEEE Journal on Selected Areas in Communications,2010,28(5):742-752.

[15]Lin Guo-hui,Xue Guo-liang.Steiner tree problem with minimum number of steiner points and bounded edge-length[J].Information Processing Letters,1999,69(2):53-57.

[16]Akkaya K,Senel F. Detecting and connecting disjoint sub-networks in wireless sensor and actor networks[J].Ad Hoc Networks,2009,7(7):1330-1346.

[17]Alfadhly A,Baroudi U,Younis M. An effective approach for tolerating simultaneous failures in wireless sensor and actor networks[C]//Proc of the 1st ACM International Workshop on Mission-Oriented Wireless Sensor Networking,2012:21-26.

[18]Mi Zhen-qiang,Yang Yang.Connectivity restorability of mobile ad hoc sensor network based on k-hop neighbor information[C]//Proc of 2011 IEEE International Conference on Communications (ICC),2011:1-5.

[19]Alfadhly A,Baroudi U,Younis M.Optimal node repositioning for tolerating node failure in wireless sensor actor network[C]//Proc of 2010 25th Biennial Symposium on Communications (QBSC),2010:67-71.

[20]Gay D M.Hooking your solver to AMPL[Z].Murray Hill:Computing Science Research Center Bell Laboratories,1997.

[21]Gay D M.IBM ILOG CPLEX optimization studio CPLEX user’s manual:Version 12.4[Z].New York:IBM,1987.

参考文献附中文.

[1]赵文栋，彭来献，田畅.无线传感器执行网络的协调机制综述[J]. 计算机应用， 2009，29(8):2183-2187.

[2]杨杰，冯勇.无线传感器与执行器网络中协同通信研究综述[J]. 计算机应用研究，2014,31(3):645-650.

[6]赵新元，王能.基于重叠区域的无线传感反应网络连接性恢复机制[J]. 计算机应用，2011,31(10):2638-2643.

[11]刘林峰，吴家臬,邹志强，等.面向节点失效问题的无线传感器网络拓扑自愈算法[J].东南大学学报(自然科学版)，2009，39(4):695-699.

赵新元(1974-),男,陕西眉县人，硕士，讲师，研究方向为无线传感器网络。E-mail:Zxy4095e1@163.com

ZHAO Xin-yuan,born in 1974,MS,lecturer,his research interest includes wireless sensor networks.