复合优化问题的Farkas引理和Lagrange强对偶
复合优化问题的Farkas引理和Lagrange强对偶*

龚鑫,方东辉
(吉首大学数学与统计学院,湖南 吉首 416000)
摘要:在函数不具有连续性的情况下,利用共轭函数的上图性质,引进新的约束规范条件,等价刻画了复合优化问题与其对偶问题之间的强对偶、稳定强对偶及Farkas引理等,并将相关结论应用于复合锥规划的研究之中.
关键词:复合优化;强对偶;Farkas引理;复合锥优化
文章编号:1007-2985(2015)06-0008-06
中图分类号:O224文献标志码:A
DOI:10.3969/j.cnki.jdxb.2015.06.003
收稿日期:*2015-06-05
基金项目:国家自然科学基金资助项目(11461027);湖南省教育厅科学研究项目(13B095);湖南省研究生创新科研基金资助项目(CX2015B548)
作者简介:龚鑫(1989—),女,河南周口人,吉首大学数学与统计学院硕士研究生,主要从事最优化理论与方法研究 通信作者:方东辉(1979—),男,湖南洞口人,吉首大学数学与统计学院教授,博士,主要从事最优化理论与方法研究.


由于许多优化问题,例如凸约束优化问题、极大极小问题、锥规划等,都可以看成复合优化问题的特例,因此复合优化问题的对偶理论引起了学者们的广泛关注[7-10].笔者在上述文献的基础上,研究如下复合优化问题(P):
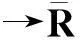
笔者在函数不一定具有连续性、集合不一定是闭集的假设下,研究复合优化问题(P)的对偶理论及Farkas引理.利用共轭函数的上图性质,引进一个新的约束规划条件,建立了问题(P)与其对偶问题之间的强对偶、稳定强对偶定理及问题(P)的Farkas引理成立的等价刻画.由于凸约束优化问题是问题(P)的特例,因此推广了凸优化中的相关结论.
1预备知识
设X,Y是实局部凸Hausdorff拓扑向量空间,X*和Y*是X和Y的共轭空间,分别赋予弱拓扑ω(X*,X)和ω(Y*,Y).
Z⊕∶={x*∈X*:
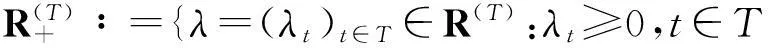
f*(x*)=sup{
epif∶={(x,r)∈X×R:f(x)≤r}.
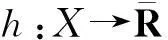
epif*+epih*⊆epi (f+h)*,
f≤h⟹f*≥h*⟺epif*⊆epih*.
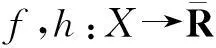
2 Farkas引理和Lagrange强对偶
设p∈X*,考虑带线性扰动的复合优化问题(Pp)
及其Lagrange对偶问题(Dp)
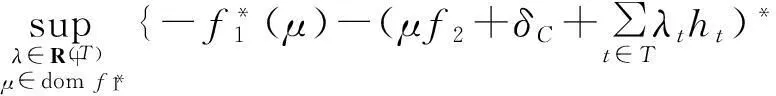
注意到,当p=0时,问题(Pp)即是前述问题(P),而问题(Dp)则转化为问题(D)

令A表示不等式系统{x∈C;ht(x)≤0,∀t∈T}的解集,即A∶={x∈C;ht(x)≤0,∀t∈T}.令v(Pp)和v(Dp)分别表示问题(Pp)和(Dp)的最优值.易证问题(P)和(D)之间的弱对偶成立,即v(P)≥v(D).若v(P)=v(D)且问题(D)有最优解,则称问题(P)和(D)之间的强对偶成立.若对∀p∈X*,问题(Pp)和(Dp)之间的强对偶成立,则称问题(P)和(D)之间的稳定强对偶成立.
受文献启发,定义复合优化问题的Farkas引理如下:
若对∀p∈X*和α∈R,下面等价关系成立:
[(f1∘f2)(x)-
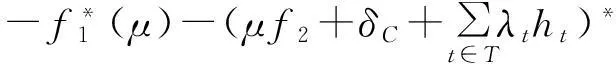
(1)
则称问题(P)满足稳定Farkas引理.特别地,当p=0时(1)式成立,则称问题(P)满足Farkas引理,即
[(f1∘f2)(x) ≥α,∀x∈AFZ(]μ∈domf*1,(λt)t∈T∈R(T)+
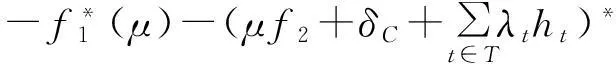
(2)
注1由共轭函数定义可知,对∀p∈X*和α∈R,
[(f1∘f2)(x)-
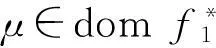

因此,(1)式成立当且仅当(1)式中的“⟹”成立.
为等价刻画问题(P)和(D)之间的强对偶及问题(P)的Farkas引理,引入以下约束规范条件:
定义1若

(3)
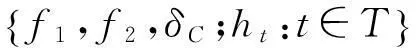
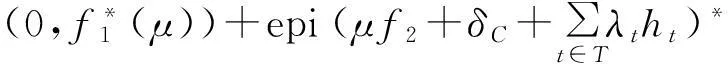
故(3)式成立当且仅当
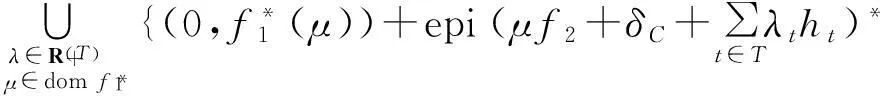

定理1下面的命题等价:
(ⅰ)问题(P)满足Farkas引理;
(ⅱ)对∀α∈R;
(0,-α) ∈epi (f1∘f2+δA)*⟺FZ(](λt)t∈T∈R(T)+,μ∈domf*1

(4)
(ⅲ)
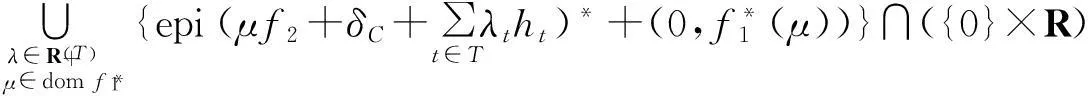
(ⅳ) 问题(P)和(D)之间的Lagrange强对偶成立.
证明首先证明(ⅰ)⟺(ⅱ).由共轭函数的上图定义知,(2)式的左边等价于(4)式的左边,(2)式的右边与(4)式的右边等价,因此(ⅰ)⟺(ⅱ).
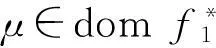

所以(ⅲ)成立.

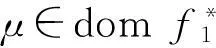
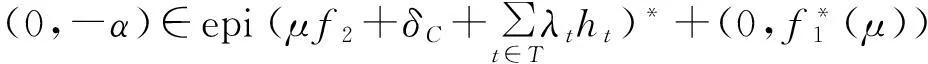
所以(4)式中的“⟹”成立.
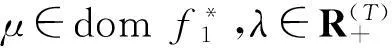
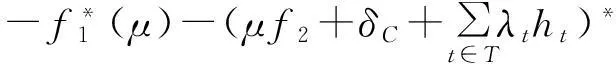
为刻画问题(P)的稳定Farkas引理及问题(P)和(D)之间的稳定强对偶,先证明以下命题:

(5)
证明对∀p∈X*,由引理1可得
epi(f1∘f2-p+δA)*=epi(f1∘f2+δA)*+epi(-p)*=epi(f1∘f2+δA)*+(-p,0),
因此,
epi(f1∘f2-p+δA)*∩({0}×R)=epi(f1∘f2+δA)*∩({p}×R)+(-p,0).
类似地,
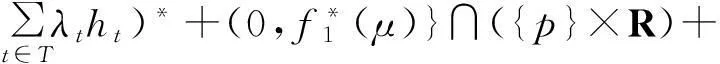
于是,(5)式成立当且仅当对∀p∈X*,

即
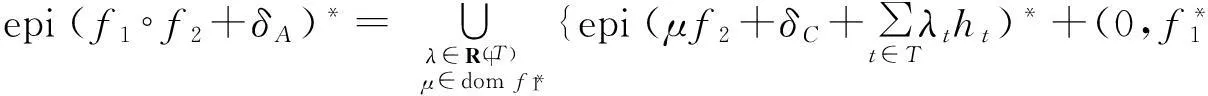
因此结论成立.
由定理1和命题1可得下面的结论:
定理2下面命题等价:
(ⅰ)问题(P)满足稳定Farkas引理;
(ⅱ)问题(P)和(D)之间的稳定Lagrange强对偶成立;
注3近来,文献研究了如下经典的约束优化问题(P1):
利用(WEHP)f条件,等价刻画了问题(P1)与其对偶问题(D1)
之间的强对偶及问题(P1)的Farkas引理,即对∀α∈R,
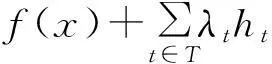
注意到,当X=Y,f1:X→R为真凸函数,f1为单位算子时,问题(P)恰为凸约束优化问题(P1),而问题(D)即为(D1).因此,定理1和定理2分别推广了文献中的定理4.4和定理4.5.
3复合锥规划中的应用

对∀λ∈S⊕,定义[2,5-6]


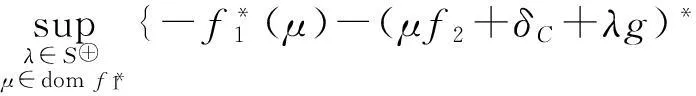
设A∶={x∈C:(λg)(x)≤0,∀λ∈S⊕}={x∈C:g(x)∈-S},则由定理1和定理2可得如下结论:
定理3下面的命题等价:
(ⅰ)问题(P(S))满足Farkas引理,即对∀α∈R,
[f(1∘f2)(x)≥α, ∀x∈A⟺FZ(]μ∈domf*1,λ∈S⊕
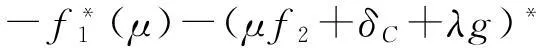
(ⅱ)对∀α∈R,
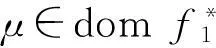
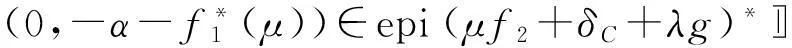
(ⅲ)

(ⅳ)问题(P(S))和(D(S))之间的Lagrange强对偶成立.
定理4下面的命题等价:
(ⅰ)问题(P(S))满足稳定Farkas引理,即对∀α∈R及p∈X*,
[f(1∘f2)(x)-p,x≥α,∀x∈A]⟺FZ(μ∈domf*1,λ∈S⊕
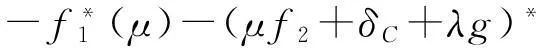
(ⅱ)问题(P(S))和(D(S))之间的稳定Lagrange强对偶成立;

注4当X=Y,f2为单位算子时,问题(P(S))和(D(S))等价于文献中的问题(Pf(S))和(Df(S)),因此定理3和定理4分别推广了文献中的定理6.6和定理6.7.
参考文献:
[1]MIGUELAGOBERNA,MARCOANTONIOLPEZ-CERD,etal.NewFarkas-TypeConstraintQualificationsinConvexInfiniteProgramming.ESAIMControlOptimisationandCalculusofVariations,2007,13(3):580-597.
[2]DHFANG,LIC,KUNGFUNG.ConstraintQualificationsforExtendedFarkas’sLemmasandLagrangianDualitiesinConvexInfiniteProgramming.SIAMJournalonOptimization,2009,20(3):1 311-1 332.
[3]RADUIOANBO,GERTWANKA.Farkas-TypeResultswithConjugateFunctions.SIAMJ.Optim.,2005,15(2):540-554.
[4]CHONGLI,KUNGFUNG,TINGKEIPONG.TheSECQ,LinearRegularityandtheStrongChipforanInfiniteSystemofClosedConvexSetsinNormedLinearSpaces.SIAMJournalonOptimization,2007,18(2):643-665.
[5]CLI,KFNG,TKPONG.ConstraintQualificationsforConvexInequalitySystemswithApplicationsinConstrainedOptimization.SIAMJournalonOptimization,2008,19(1):163-187.
[6]姚元金.(F,α,ρ,d)-凸性下的非光滑多目标分式规划问题的对偶.湖北民族学院学报:自然科学版,2014,32(2):124-127.
[7]RADUIOANBO,SORIN-MIHAIGRAD,GERTWANKA.ANewConstraintQualificationfortheFormulaoftheSubdifferentialofComposedConvexFunctionsinInfiniteDimensionalSpaces.MathematischeNachrichten,2008,281(8):1 088-1 107.
[8]BLEMAIRE.ApplicationofaSubdifferentialofaConvexCompositeFunctionaltoOptimalControlinVariationalInequalities//NondifferentiableOptimization:MotivationsandApplications.Berlin:Springer,1985:103-117.
[9]ZHOUYuying,LIGang.TheToland-Fenchel-LagrangeDualityofDCProgramsforCompositeConvexFunctions.NumericalAlgebra,2014,4(1):9-23.
[10]FITZPATRICKSP,SIMONSS.TheConjugates,CompositionsandMarginalsofConvexFunctions.J.ConvexAnal.,2001,8:423-446.
[11]CZALINESCU.ConvexAnalysisinGeneralVectorSpaces.RiverEdge,NewJersey:WorldScientific,2002.
Farkas Lemmas and Lagrange Dualities for
Composite Optimization Problems
GONG Xin,FANG Donghui
(College of Mathematics and Statistics,Jishou University,Jishou 416000,Hunan China)
Abstract:Under the assumption that the functions are not necessarily continuous,by using the epigraph technique of conjugated functions,we introduce some new constraint qualifications,which completely characterize the Farkas lemma,the strong duality and the stable strong duality between the composite problem and its dual problem.Applications to the composite conical optimization problem are also given.
Key words:composite optimization;strong duality;Farkas lemma;composite conical optimization
(责任编辑向阳洁)


