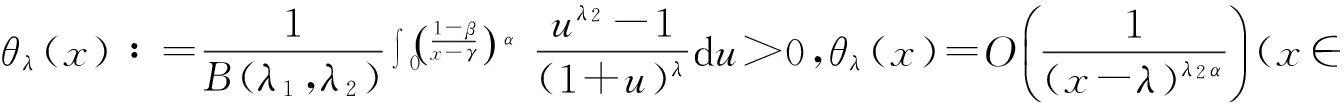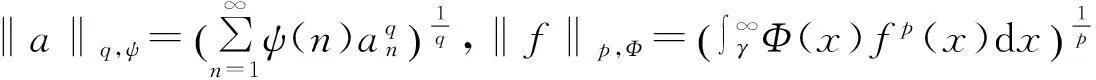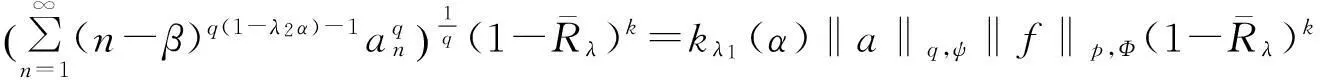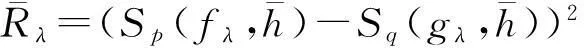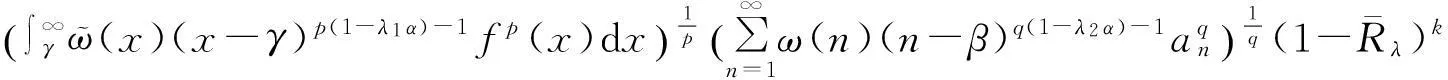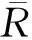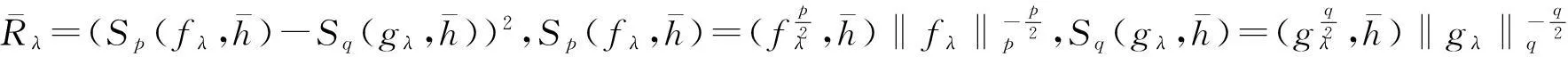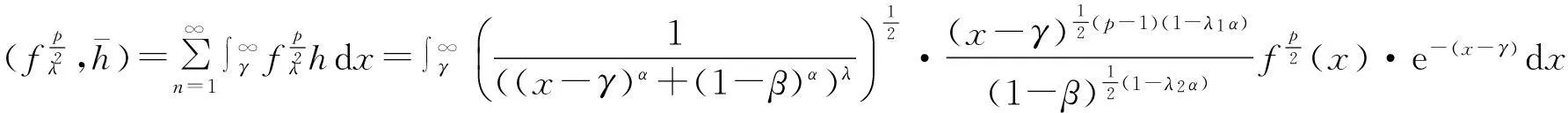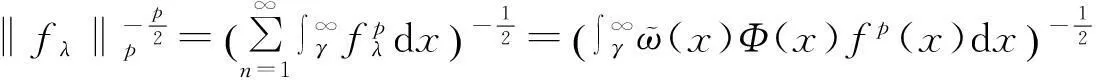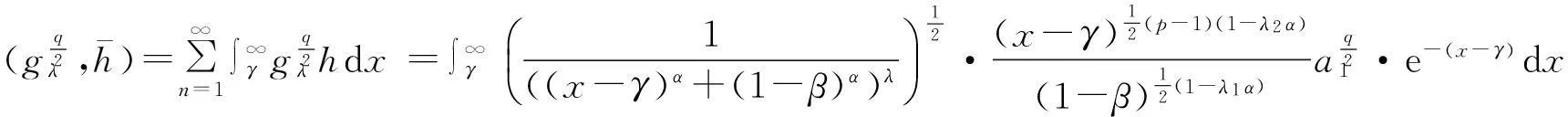半离散含多参数的Hilbert型不等式的改进

半离散含多参数的Hilbert型不等式的改进*

聂彩云

(吉首大学数学与统计学院，湖南 吉首 416000)

摘要：利用权函数的方法、参量化的思想和加强的Hölder不等式对半离散的Hilbert-type 不等式作了改进，建立了一些新的不等式.

关键词：Hilbert-type不等式；权系数；Hölder不等式；β函数

文章编号：1007-2985(2015)06-0005-03

中图分类号：O178文献标志码：A

DOI:10.3969/j.cnki.jdxb.2015.06.002

收稿日期：*2015-08-05

作者简介：聂彩云(1963—)，女，湖南永顺人，吉首大学数学与统计学院副教授，主要从事函数论及应用研究.

1问题的提出

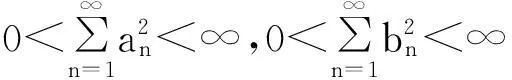
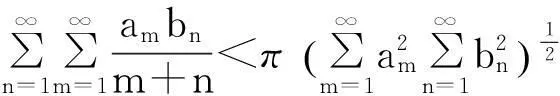
这里常数因子π是最佳值.

文献中建立了一个新的Hilbert型不等式：

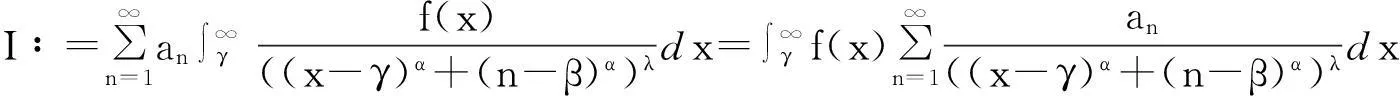
kλ1(α)‖f‖p,φ‖a‖q,ψ，

(1)

这里常数因子kλ1(α)是最佳值.

笔者利用改进的Hölder不等式对(1)式进行加强，从而建立一些新的不等式.

2相关引理

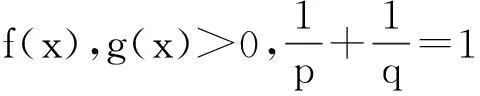
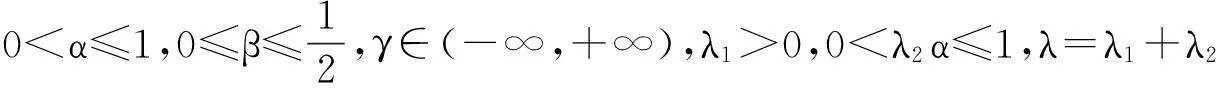
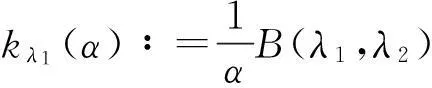
0

证明过程见文献.

3主要结果

为方便起见，再引入一些符号：

Φ(x)∶=(x-γ)p(1-λ1α)-1 ，ψ(n)∶=(n-β)q(1-λ2α)-1 ，

(2)

(3)

证明由引理1和引理2，有

即(2)式成立.

由引理1，有

因此，

定理1得证.

注1(2)式即为(1)式的改进式.

参考文献：

[1]HUANG Qiliang，YANG Bicheng.On a More Accurate Half-Discrete Hilbert’s Inequality.Journal of Inequality and Applications，2012(1)：106-117.

[2]HE Leping,GAO Mingzhe，JIA Weijian.On a New Strengthened Hardy-Hilbert’s Inequality.Journal of Mathematical Research and Exposition，2006,26(2):276-282.

[3]LIU Tuo,YANG Bicheng，HE Leping.On a Half-Discrete Reverse Mulholland-Type Inequality and an Extension.Journal of Inequalities and Applications,2014(1):103-111.

[4]LIU Tuo,YANG Bicheng，HE Leping.On a Multidimensional Hilbert-Type Integral Inequality with Logarithe Function.Mathematical Inequalities & Applications，2015,18(4):1 219-1 234.

Improved Half-Discrete Hilbert-Type Inequality with Multi-Parameters

NIE Caiyun

(College of Mathematics and Statistics,Jishou University,Jishou 416000，Hunan China)

Abstract:By using weight functions,parametrization and sharpened Hölder’s inequality,some improvements of Hardy-Hilbert’s inequality are given,and a few new inequalities are established.

Key words：Hilbert-type inequality;weight coefficient;Hölder inequality;βfunction

(责任编辑向阳洁)