基于PCSA算法的分布式电源优化配置研究

基于PCSA算法的分布式电源优化配置研究

李春辉

(东北电力大学 电气工程学院，吉林 吉林 132012)

摘要：以优化分布式电源配置作为基础，针对电力系统配电网所产生的影响进行研究，并按照各个因素提出对应的目标函数所需的数学模型，将克隆选择与粒子群两种不同算法的特性相结合，将优化电源配置遇到的问题通过PCSA混合优化方式处理，从而可以充分发挥其价值的有效使用率。确定目标函数为最小静态电压指标与有功网损，从而创建数学模型，与PCSA算法相结合，对优化遇到的问题进行求解。基于当前粒子群算法收敛速度快速提高后，通过加入克隆复制的方式，从而保护已优化的个体，对计算后值的准确性提升，最终确定接入DG的最佳位置。配电系统通过IEEE33节点作为算例，对该模型与算法中的实用性与有效性进行验证。

关键词：分布式电源;配电网;PCSA;优化配置;模型

收稿日期：2015-05-23

作者简介：李春辉(1983-)，女，吉林吉林人，硕士研究生。

DOI：10.13888/j.cnki.jsie(ns).2015.04.003

中图分类号：TM715

文献标识码：A

文章编号：1673-1603(2015)04-0303-05

Abstract：Based on the distributed power allocation optimization,most experts carried on research the impact generated by the distribution network of power system,and proposed corresponding objective function mathematical model according to the various factors.By combining with the different characteristics of the clonal selection and particle swarm algorithms,the power allocation optimization could solve by PCSA hybrid optimization approach,which could give full play to its effective utilization.The optimization could implement with the PCSA algorithm combined with a mathematical model created with the objective function of the minimum static voltage index and the active power loss.Based on the particle swarm algorithm,the convergence speed increased rapidly,by the addition of clonally replicated,so as to protect individuals have been optimized,to enhance the accuracy of the calculated value,and ultimately determine the optimal placement of DG.The utility and validity of the distribution system is verified with the method by taking the IEEE33 node as an example.

分布式能源作为一种主要的提供能源范式，主要用于客户端，运行方式为并网或孤岛，可整理并优化不同客户所需的能源与配置资源情况[1]。并网采用分布式电源，在电网上输配的潮流下降，与此同时网损也下降[2]。DG与电网接入后，会影响各个方面，主要包括网络损耗、系统保护、系统稳定性以及电压分布等，DG容量、位置等会影响其程度。世界上各个国家科研人员将重点放在接入分布式电源、配置电源以及最优的接入方案方面等。基于从整体上总结国内外发展情况，并对配电网中应用的优化方式、配置模型进行研究，并更加深入的对优化DG时产生的问题与发展状态进行分析[3]。

用有功损耗最小来衡量网络损耗的大小，从降低配电网网损目的出发，用静态电压稳定指标来衡量系统电压的稳定性，把主要的约束条件设为潮流，建立了一种计算简捷、效果实用的数学模型，然后结合PCSA算法对其进行求解，最后配电系统通过IEEE33节点对模型进行有效性的验证。算例结果表明：方法的流程清晰、计算简单精确，充分将其实用价值体现出来，而且分布式电源的合理接入可以实现电压水平的改善和系统网损的降低[4]。

1基本粒子群算法

在粒子群算法(PSO)中[5]，每个锁定为优化的解被看做是搜索空间内的一个粒子，所有的粒子都相对应着优化问题的一个值，而粒子的速度决定着它的飞行方向和距离，通过追寻群体中的最优粒子的位置来实现在解空间的搜索。

(1)

(2)

其中：i=1，2，…，m，i表示粒子的编号；d表示搜索空间的维分量，d=1，2，…，N；k为当前进化代数；Xi，Vi向量，表示粒子i的位置与速度；r1和r2为分布于(0，1)之间的随机数；c1和c2为学习因子；ω是惯性权重称为惯性权重(inertia weight)，其作用是调整算法全局和局部搜索能力的平衡。式(1)和式(2)组成基本的PSO算法。

经实例验证，惯性权重ω对此算法的优化性能有直接的影响力，ω越大则粒子的全局搜索能力越强，而ω较小时则有利于局部搜索。因此，采用自适应调整ω的方法，让ω与迭代次数的关系呈线性关系变化来改善算法的收敛性能。

ω=ωmax-iiter(ωmax-ωmin)/iitermax

(3)

式中，ωmin和ωmax为ω的起始值和终止值，iitermax为最大迭代次数，iiter为当前迭代次数。

2克隆选择算法

克隆选择算法是专家学者模拟生物免疫系统，经过大量研究实证得出的克隆选择原理，抗原为待优化的约束条件与目标函数[6]。

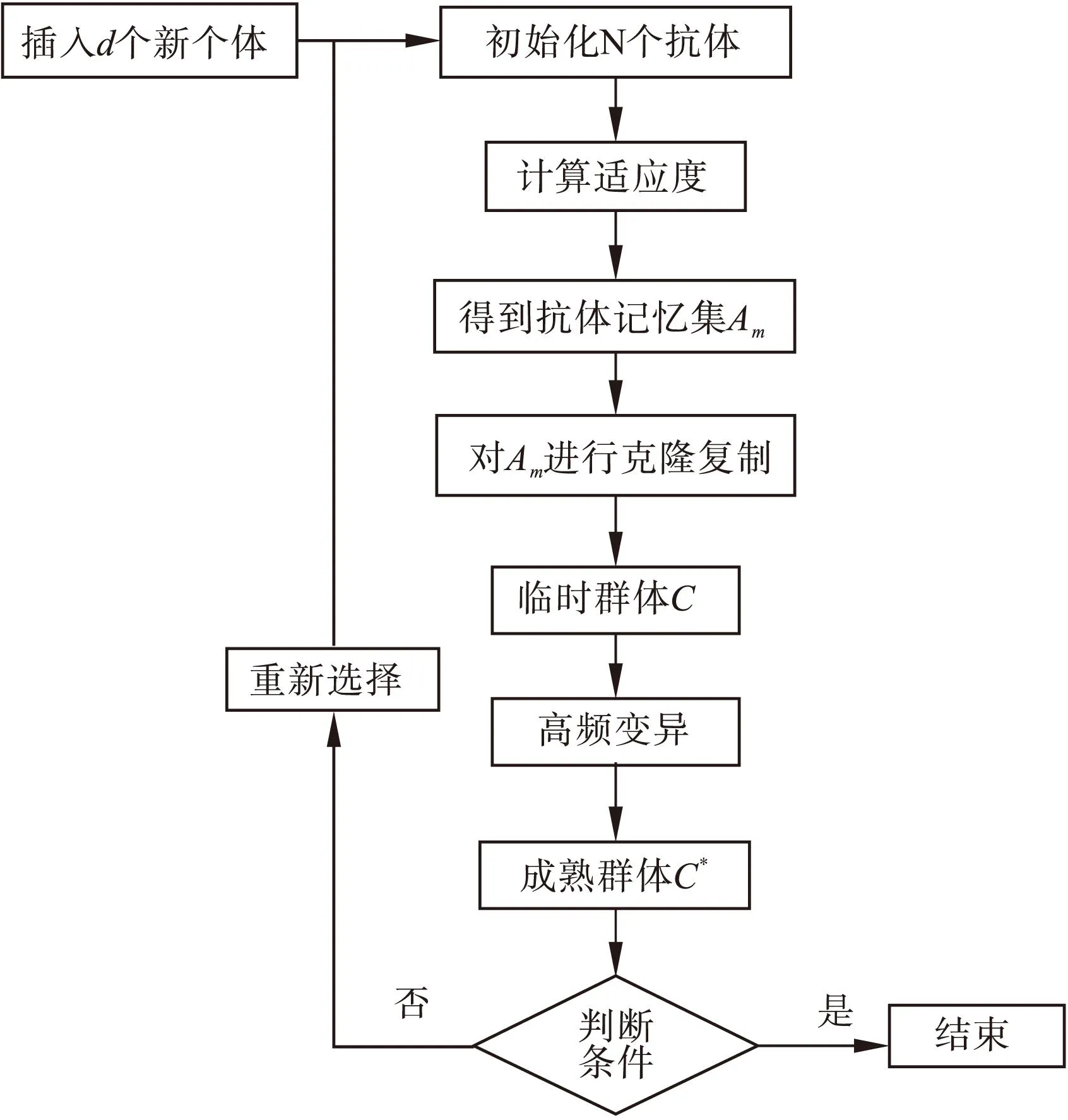
图1　CSA算法的流程

3PCSA算法

该算法是粒子群与克隆选择算法的混合，应用克隆选择机制后的优势在于，粒子群的多样性得到保护，粒子收敛速度得到提升。克隆时抗体为粒子群，抗原为约束条件与目标函数，根据不同的适应度采用正比方式排列适应度高的抗体并克隆，若与适应度成反比则表示变异。一些抗体具有较低适应度，需要根据一定比例再次初始化，可保持其多样性。通过上述方式可以得到一种混合的优化算法PCSA，包含克隆选择与粒子群[7-10]。

PCSA算法的原理：初始化抗体后，通过粒子群算法对“飞行”方向进行引导，可提升收敛速度，克隆部分适应度较高的抗体，从而在“优”周围聚集较多抗体，已完成克隆的抗体操作变异，将抗体向“优”周围的不同方向探索。一些适应度较差的抗体被抛弃，并对其初始化，让群具有一定的多样性。

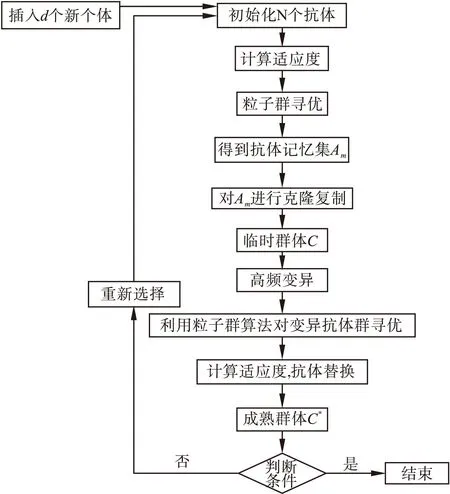
图2　PCSA算法流程

DG优化配置问题是一个变量较多、约束繁琐、非线性组合的优化问题[11]。最近十几年内，部分国内外专家开始对群体智能算法进行研究，该算法的理论为，对自然界内生物群体行为进行模拟，成为随机优化算法的一部分。目标确定后通过群体行为完成寻优搜索算法作为群体智能算法的基础，该过程中表现出一定特性，主要为并行性、随机性以及分布式等。而粒子群算法不能保证收敛到全局最优解，甚至于局部最优解，因此许多学者经过验证提出了不少改进其算法收敛性能的方法。

4分布式电源优化配置

在电力系统配电网上接入分布式电源后，其中任何一个负荷节点均可以使电网系统网络损耗降低，从而对电压分布情况进行调整。主要因素在于分布式电源可对不同负荷节点所消耗的功率平衡，从而起到改善节点负荷水平，让相关电路产生的有用功率降低，受到有用功影响导致功率损耗与电压均降低。

选择分布式电源最佳位置的出发点时，需要在该节点上添加单位注入功率，可提高系统损耗量，同时成为最大值[12]。按照网损灵敏度的基本物理意义，可调节网络损耗值最高的效力节点，可以最大程度降低系统有功损耗。控制变量调节时，采用的顺序为由大到小，主要的作用在于对有功网损降低，降低由于接入分布式电源后对系统产生的振荡现象，同时在实际应用中具有意义。根据网损灵敏度值最终确定分布式电源的最优位置。

主要考虑在不改变系统馈线运行方式、不影响系统经济成本的前提下分布式电源优化配置的问题，因为分布式电源就地平衡了部分负荷，所以采取用有功损耗最小来衡量网络损耗的大小，用静态电压稳定指标来衡量系统电压的稳定性，建立以有功损耗最小和静态电压稳定指标最小为目标的数学模型[13]。

4.1目标函数

1)有功损耗最小。

目标函数如下：

2ViVjcos(θi-θj)]

(4)

式中：PL为系统有功损耗，N为系统支路数；Gm(i，j)为第m 条线路i、j的电导;Vi、θi为i节点电压幅值和相角。

2)静态电压稳定指标最小。

静态电压稳定指标：

(5)

其中，Ut,m表示第m条支路(首节点为i,末节点为j)的电压稳定指标；R、X分别为支路k的电阻和电抗；Pj、Qj分别为流入末节点的有功和无功；Ui为首节点电压幅值。

4.2约束条件

有功功率和无功功率潮流平衡方程如下：

(6)

不等式约束条件为节点电压的上下限和DG容量的上下限，即：

(7)

其中，系统有n个节点，n为平衡节点编号。mi为0-1变量，如果DG从i点接入系统则mi=l，否则为0。Pi，Qi分别表示系统向节点i注入的有功和无功功率；PDG、QDG分别为DG向节点注入的有功和无功功率；PLi，QLi分别为节点i的有功和无功负荷功率。

5算例分析

由于有功网损最小和静态电压稳定指标最小两个目标在优化中彼此没有可结合比较的可能性，而单独优化很难使系统总体达到最优。

为验证PCSA算法可实现的优越性[14]，通过配电系统的IEEE33节点作为算例，如图3所示。PCSA算法的种群最大迭代次数iitermax为50，种群规模N为20，选择率a=0.5，克隆常数β=0.3，抗体变异常数c=8；粒子群方程参数ωmin= 0.4，ωmax=0.9；c1=c2=2。

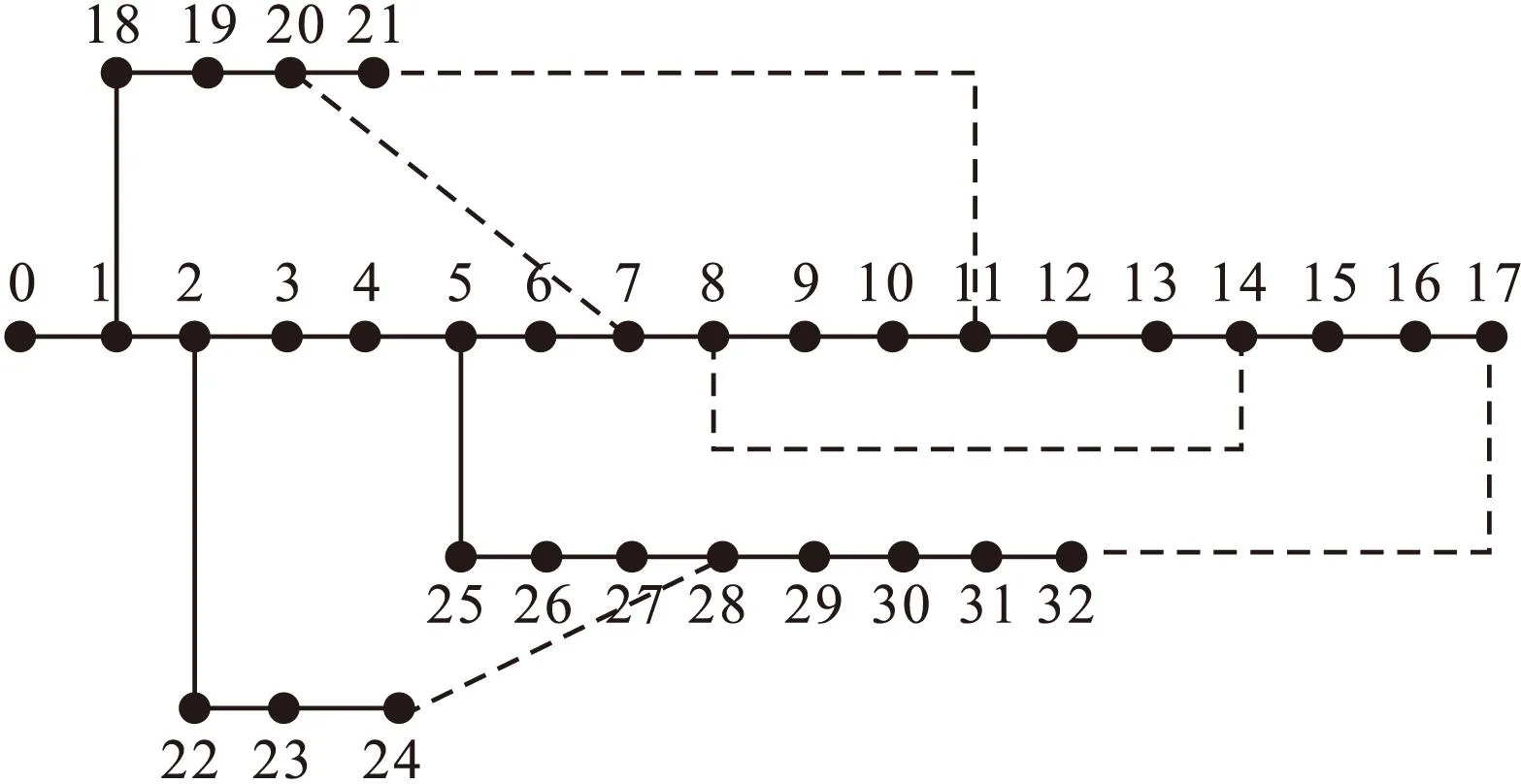
图3　IEEE33节点配电系统

算例结果表明：采用的DG配置的优化方法其降损效果优于其它任意的配置方法，而降损率可以有效的改善系统的电压水平。由图4可以看出,经过PCSA算法以有功网损最小为目标进行优化得出接入DG最优位置为28节点,此时的有功损耗为43.9214 kW,静态电压稳定指标为0.0105。可以看出28节点时系统的有功网损最小[15-16]。

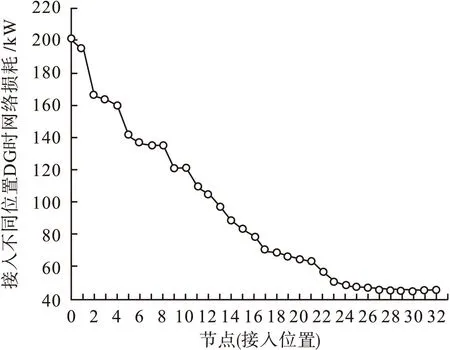
图4　系统有功网损波形

表1中显示三种不同算法，分别为PSO、PSCA以及SCA，通过二十次迭代后获得已优化的网损最差值、最优值以及平均值。通过该表对比可得，PCSA算法与其他两种算法对比，具有一定优势，表现在计算精度与收敛稳定性方面。

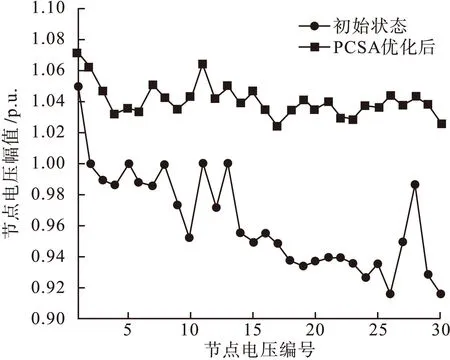
图5　优化前后电压值

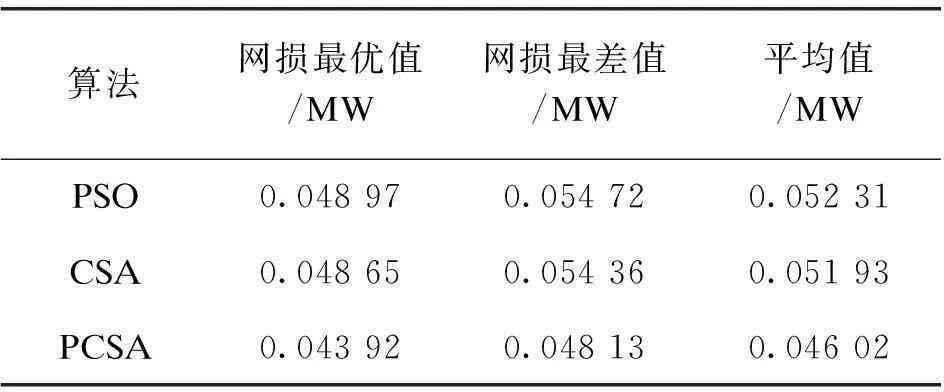
表1　三种算法的有功网损最优、最差及平均值的比较

6结论

处理优化分布式电源配置问题采用的方式为混合算法，主要包括克隆选择算法与粒子群算法。PCSA算法应用时的基础为具有较好收敛性的集结粒子群，使用克隆选择算法后可保护个体，同时计算的准确性也得到提升。通过试验表明，该方法在复杂性较高的配电网络中应用最佳，与节点IEEE33系统算法相结合，在求解优化分布式电源配置问题中对其使用方法具有较强搜索能力进行验证，从而在优化分布式电源配置过程中准确性更高，速度更快，同时产生的网络损耗值下降，电压水平也得到改善。计算过程表现出有效性、可靠性以及稳定性。

参考文献

[1]陈春泉,殷豪,陈清泉.分布式电源配置优化研究现状与展望[J].广东电力,2013,26(3):45-49.

[2]庄雷明.城市电网规划中分布式电源容量的优化配置[D].北京：华北电力大学，2010.

[3]宋祺鹏，宋晓辉，杨亮.分布式电源对配电网规划的影响[J].电气时代，2010(4)：74-75.

[4]Abu-Mouti F S，El-Hawary M E.A new and fast power flow solution algorithm for radial distribution feeders including distributed generations[J].Proceedings of the IEEE International Conference on Systems，Man and Cybernetics，2007(12)：2668-2673.

[5]白艳敏.粒子群算法及其应用研究[D].兰州：兰州交通大学,2013.

[6]张燕.基于免疫克隆选择算法的研究与应用[D].山西师范大学,2013.

[7]雷德明,严新平.多目标智能优化算法及其应用[M].北京:科学出版社,2009.

[8]吴晶.基于混合算法的配电网优化规划[D].保定:华北电力大学,2009.

[9]张伟星.基于粒子群优化算法的动态多目标优化算法研究及应用[D].郑州：郑州大学,2013.

[10]刘楠楠.克隆选择多目标优化算法及其应用研究[D].宁波：宁波大学,2013.

[11]顾承红,艾芊.配电网中分布式电源最优布置[J].上海交通大学学报,2007,41(11):1896-1900.

[12]朱勇,杨京艳,张冬清.基于有功网损最优的分布式电源规划[J].电力系统保护与控制,2011,39(21):12-16.

[13]罗明亮，黄宇保，王建全.基于最优潮流法含暂态稳定约束的最大传输容量计算[J].电力系统保护与控制，2010，38(19)：22-26.

[14]汪兴旺,邱晓燕.基于改进粒子群算法的配电网分布式电源规划[J].电力系统保护与控制,2009(14):16-20.

[15]张立梅,唐巍,赵云军，等.分布式发电接入配电网后对系统电压及损耗的影响分析[J].电力系统保护与控制,2011,39(5):91-96.

[16]WANG Fang,YE Jing .Fast solution for optimal placement of distributed generation[C]//Proceedings 2011 IEEE Power Engineering and Automation Conference.Wuhan,2011,3:1-4.

Research on Optimal Allocation of Distributed

Generation Based on PCSA Algorithm

LI Chu-hui

(School of Electrical Engineering,Northeast Dianli University,Jinlin 132012,Jinlin Province)

Key words： distributed generation;distribution network;PCSA;optimal configuration;models

(责任编辑佟金锴校对张凯)