让提问鲜活有力

李海东

所谓“问题情境”，就是教师所提供的问题，与学生已有的认知结构产生矛盾冲突，学生仅凭自己所掌握的数学知识和数学技能暂时无法解决，从而产生强烈求知欲望而形成一种教学情境。所谓“从数学角度提出问题”，就是学生根据问题情境发现并用数学语言表达出来的问题，简单地说就是数学问题。数学问题有三种：模仿性数学问题、发展性数学问题和创造性数学问题。现结合自己的教学实践，谈谈如何结合现实创设问题情境，促进学生提出不同层次的数学问题。

一、结合虚拟现实创设问题情境，促进学生提出模仿性数学问题

模仿性数学问题，也叫常规性数学问题，就是学生通过模仿教师、课本或同学提问而提出的本质相同的数学问题。善于模仿是学生的天性。小学生学习新知识或者新技能，往往都是从模仿开始的。提问也是如此。根据学生的年龄特点，教师如果能用一些深受他们喜爱的卡通形象，创设虚拟现实的问题情境，为学生呈现一些具有刺激性的数学信息，就能为学生提供发现数学问题、提出数学问题的背景和重要基础，就能激发学生的提问兴趣，促使学生迅速提出一些模仿性数学问题。

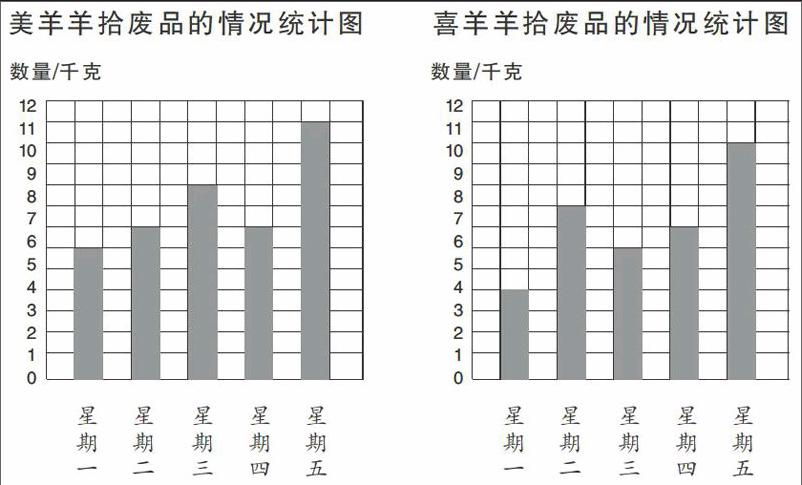
教学“平均数”时，为了培养学生的练习兴趣，我这样创设问题情境：

（1）美羊羊平均每天拾废品多少千克？

（2）喜羊羊哪几天拾废品的数量超过平均数？

（3）你还能提出什么问题？

小学生的模仿能力特别强，他们看着习题中的问题，很快就能依葫芦画瓢地提出“喜羊羊平均每天拾废品多少千克？”“美羊羊哪几天拾废品的数量超过平均数？”……当一个同学提出“星期一喜羊羊和美羊羊拾废品的平均数是多少？”时，其他人通过模仿立即就能提出“星期二喜羊羊和美羊羊拾废品的平均数是多少？”“星期三喜羊羊和美羊羊拾废品的平均数是多少？”……根据具有童话色彩的虚拟现实创设问题情境，不仅能拓展学生的学习空间，而且能有效激发学生发现问题和提出问题的积极性和主动性，使其能迅速提出一些模仿性数学问题。

二、结合生活现实创设问题情境，促进学生提出发展性数学问题

发展性数学问题，就是比常规性问题更具有思维深度、更具有探索性的数学问题。发展性数学问题不会凭空而来，学生往往需要结合自己的生活现实才可能提出，因为学生亲身经历的现实生活是学生经验系统中最亲切和最直接的内容。学习内容和学生熟悉的生活情境越贴近，学生自觉接纳知识的程度就越高，发现问题和提出问题的可能性就越大。因此，我们要根据学生的年龄特征，选择他们熟悉的、感兴趣的生活现实创设问题情境，使问题情境不但能承载相应的数学知识，而且能有效激发学生提出一些由生活现实引发的数学问题，甚至能促使学生脱离简单模仿而提出一些发展性数学问题。

教学“两步计算的实际问题”时，我创设了这样一个问题情境：下图是小红到超市购物看到的一些商品价格，请大家根据信息编一道两步计算的数学故事。学生所编故事中的问题都是买两种商品一共多少元。如买1个书包和2本笔记本一共多少元，或者买2个书包和1本笔记本一共要多少元？虽然学生没有模仿的对象，提出的问题也有一定的思考价值，但都是求和问题，在本质上是同一种类型。如何发散学生思维、引导学生进一步提出发展性数学问题呢？我引导学生回顾生活中的购物情境：有的学生说购物时可能会出现钱没带够的现象，有的学生说可能给售货员的钱多了要找回钱，有的学生说买的东西觉得不好要调换……在此基础上，我要求学生以小组为单位，根据购物时可能出现的情况，编两步计算的数学故事，看哪个小组能提出不同的问题。学生先独立思考，然后小组交流，最后全班汇报，学生所编故事和提出的数学问题是这样的：1.妈妈带了100元钱，买4个书包，够不够？2.小红去商场买3本笔记本和1个书包，一共要付给营业员多少元？3.东东带了100元，买2盒钢笔，要找回多少元？4.买2个书包的价钱相当于可以买几个本子？5.我带了50元钱，买2盒钢笔，还差多少元？学生提出的问题除了求和问题，还有相差问题、两种量比较的问题和替换问题等，这比简单模仿所提出的问题具有发展性。

联系学生的生活现实创设问题情境，不但能帮助学生拉近生活与数学的距离，而且能帮助学生把自己在生活中的所见所闻与提问联系起来，使枯燥的数学提问变得鲜活生动，学生的数学思维也得到了充分发展。

三、结合数学现实创设问题情境，促进学生提出创造性数学问题

创造性数学问题，就是学生提出的一些别人没有想到的、具有一定原创性的数学问题，其思维价值比模仿性问题和发展性问题更大。创造性数学问题是学生在数学现实（即所掌握数学知识、方法、技能和数学活动经验等）的基础上，按照其内部规律实现对数学理解基础上提出的。这就要求教师从学情出发，灵活选择学生的数学现实创设问题情境，引导学生通过观察、比较、抽象、概括、类比和归纳等活动，理解和掌握数学知识，体会数学知识间的内在联系，自主建构数学认知结构，从而主动提出一些创造性的数学问题，发展学生的数学思维。

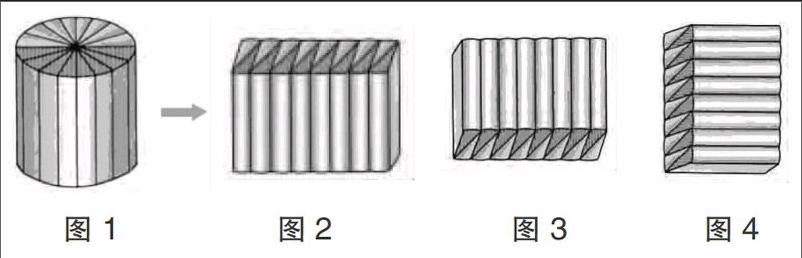
教学“圆柱的体积”时，学生熟练掌握、应用体积公式后，我说：“通过学习，大家已经掌握了圆柱的体积计算方法。你有什么不懂的地方或者有什么不同想法吗？”话音刚落，一位学生举手提问：“三角形面积和梯形面积公式都有不同的推导方法，圆柱的体积公式有不同推导方法吗？”我的提问有鼓励学生提问的成分，因此，学生的提问在我意料之中，但我提问的主要目的是想了解学生的学习情况，以便确定后续教学：如果少数学生有不懂的地方，我就帮他们查漏补缺；如果学生没有不懂的地方，我就用作业检测他们对知识的掌握情况。结果，学生根据自己的数学现实提出问题，确实出乎我的意料。因为体积知识需要学生具备一定的空间观念，而小学生的空间思维能力有限，从没有学生主动提出类似问题。想了想，我问学生：“你能想到什么不同的推导公式的方法吗？”学生边做手势边回答说：“把圆柱倒下来放，能不能转化成长方体并推导公式呢？”根据学生的发言，我引导学生把教材中的插图侧过来看（图3），大家经过讨论，认为无论圆柱怎么放，体积都不变，都可以用V=πr²h表示，因为它们所表示的是同一个圆柱的体积。区别在于图2的底面积是圆的面积，图3的底面积是圆柱侧面积的一半，高是圆柱的底面半径，体积就是侧面积的一半×高，用字母表示就是V=2πrh÷2×r=πr²h。结合学生的发言，我趁热打铁：“大家现在还有什么问题想问吗？”另一个同学先把课本插图侧着放（图4）再问：“老师，如果把圆柱这样转化成长方体，怎么推导圆柱的体积公式呢？”学生通过观察和思考，很快发现长方体的长就是圆柱的高，宽就是圆柱的底面半径，高就是圆柱底面周长的一半，因此，圆柱的体积=长方体的体积V=rh×（2πr÷2）=πr²h。结合数学现实创设问题情境，学生提出了创造性数学问题，从而从新的角度进一步认识圆柱体积公式的推导方法，发展了学生的提问能力，培养了学生的空间观念。

总之，教师结合虚拟现实、生活现实或数学现实创设问题情境，努力使情境内容与形式高度统一，才能为学生提出数学问题提供相应的信息和依据，才能激发其问题意识，才能促进其提出不同的数学问题，从而有效培养学生的提问能力。