强夯加固状态实时监控方法研究
李进亮
(河北省水利工程局, 河北 石家庄 050021)
强夯加固状态实时监控方法研究
李进亮
(河北省水利工程局, 河北 石家庄050021)
【摘要】在描述夯锤对夯点土体的动力作用的基础上,阐明了夯锤自一定高度下落到与地面接触时开始的减速运动过程中的一系列动力过程和效应,阐述了强夯振动传播和衰减规律,系统介绍了强夯振动频域分析的理论,建立了夯点锤土复合体的振动模型,分析了夯点土体振动特征与夯点土体加固状态之间的物理联系,实现了地基强夯加固状态的实时振动监控。
【关键词】强夯加固; 振动频域; 监控方法
1前言
强夯施工过程中土体加固状态主要按夯沉量监控[1]。这种监控方法一是效率低,每次夯沉量测量均需停锤等候,影响施工速度;二是测量指标误差大;三是监控指标与地基加固效果没有直接的联系,夯沉量与地基土体的压实度、湿陷性系数的关系有待研究。因此,工程上急需一套高精度、高效率、低成本的强夯施工过程中的夯点土体加固状态监控方法。
根据振动理论,强夯土体的动力特征与土体的夯实状态密切相关:随土体的夯实程度提高,其振动强度和振动频率都有所提高。地基强夯加固状态实时监测技术关键就是设法利用离开夯点一定距离以外的测点上观测的振动时程,推求出夯点土体的振动时程,从而获得夯点土体夯实参数与振动特征参数的相关关系,为利用振动特征参数确定夯点土体奠定基础。
2强夯振动的传播规律
2.1强夯振动波场
强夯振动是一种冲击式的点源振动,在落锤与土体接触的瞬间产生强大的冲击作用(冲量I=mv0,其中m为夯锤质量,v0为夯锤与地面接触时的下落速度),使得夯点局部土体组构破坏重组,同时,引起夯点土体的强烈振动(震源振动)。夯点土体的振动向周围场地土体中扩散传播,形成场地岩土体中的强夯波动场(图1),引起远离夯点的土体的弹性振动。在这一动力过程中,夯锤具有的势能转化为地基土体的变形能(结构重组、塑性变形耗能)和向夯点以外的地基空间中扩散传播的弹性波动能量。

图1 强夯振动波场示意图
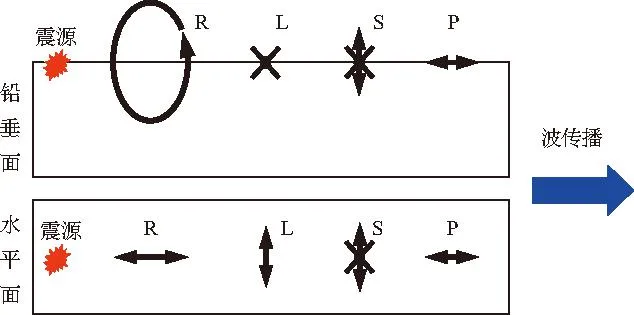
图2 各类弹性波质点振动方式和传播速度快慢的比较
如图1所示,弹性波动能以体波(纵波P、横波S)和面波(瑞雷波R、勒夫波L)的形式向夯点周围地基土体中扩散传播。不同类型的弹性波动传播速度的相对快慢和质点振动方式如图2所示,其中S波可进一步分解为在铅垂平面内振动的SV波和在水平面内振动的SH波。强夯激振的特殊方式(重锤垂直下落)决定了强夯振动波场中SH波和L波几乎不存在。因为,这两种类型波动的质点振动方向垂直于波动传播方向,质点振动轨迹平行于地面。P波在场地岩土体中引起与波传播方向一致的质点振动;S波引起与波传播方向相垂直的质点振动;R波在地表附近引起的质点振动轨迹为长轴垂直于地面的逆进椭圆。在一定范围内,它们先后作用于场地土体中,并在一定的持续时间段上产生叠加,形成一个完整的强夯地面振动波场。
P波、S波自夯点出发向场地岩土内各个方向扩散传播(波前面近似为球面),随着传播距离的增加,能量(振幅)衰减很快,衰减速率与传播距离的平方(r2)成反比;R波自夯点出发,沿着地面方向外围扩散(波前面近似为柱面),能量集中在地表附近(振幅随深度迅速衰减),随着离开夯点的传播距离的增加,能量逐步衰减,衰减的速率与传播距离(r)成反比,可见瑞雷波的衰减速率远比纵波、横波的衰减速率小,所以在地面附近对测点强夯振动贡献最大的是瑞雷波。波场中不同类型的波动能量分配大致为:P波占6.9%,S波占25.8%,R波占67.3%[2-3]。因此,S波和R波是构成强夯振动的主要波动成分。
2.2强夯振动随夯检距的衰减
由于土体内部阻尼的作用,强夯振动在向外传播的过程中,随着传播距离的增加振动强度会逐渐减小,表现为强夯振动随传播距离增加的空间衰减过程。
监测研究表明,强夯振动质点振动速度随夯检距r(夯点至振动监测点的水平距离)的变化满足负幂指数关系:
(1)
式中,β为衰减指数,k为当量系数,vm为夯点的最大振速。
3强夯振动的频域分析
强夯振动频域分析理论可以为夯点振动(震源函数)反演提供理论依据[4]。强夯振动频域分析理论将强夯场地视为一个线性系统,夯点落锤激发的夯点土体振动是这个系统受到的激励(输入),在离开夯点一定距离上测点的振动是系统对激励的响应(输出),夯点的振动输入(震源函数)通过系统的作用产生测点的振动输出(测点振动时程)。系统的作用是夯点激励和测点响应之间的桥梁,利用这一桥梁,就可以根据测点上的振动输出反推出夯点的振动过程。
3.1强夯振动频域分析模型
强夯地面振动是由多种频率成分叠加组成的复杂振动,把强夯地面振动的研究从时域引入频域范围,建立强夯振动频域分析模型,得出强夯震源激励函数的具体表达式。
如图3所示,将岩土体与振动观测仪器视为一个动力系统,强夯作用看作是对系统的激励,测点上的质点振动就是在激励作用下系统的输出。激励—系统—响应即为强夯作用下场地岩土体振动的物理概化模型。

图3 强夯振动物理模型
在时间(t)域内,激励和响应可分别用激励函数s(t)和响应函数u(t)描述。设岩土体和观测仪器构成的系统为线性的,则u(t)、s(t)应满足以下褶积关系:
在时间(t)域内,激励和响应可分别用激励函数s(t)和响应函数u(t)描述。设岩土体和观测仪器构成的系统为线性的,则u(t)、s(t)应满足以下褶积关系:
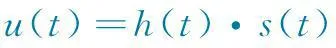
(2)
式中,h(t)为系统的传递函数。
在频率f域内,通过傅立叶变换,u(t)、s(t)和h(t)分别对应有响应谱U(f)、激励谱S(f)和传递谱H(f),三个谱满足以下关系:

(3)
传递谱H(f)可进一步表示为仪器接收谱I(f)和介质作用谱Q(f)的积,令V(f)=U(f)/I(f),代入式(3)可得:
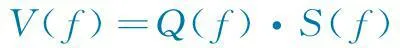
(4)
式中,V(f)为消除掉仪器影响后岩土体介质测点上的质点振动过程v(t)所对应的介质响应谱。与Q(f)对应,消除掉仪器影响后,系统传递函数h(t)中只保留了介质作用函数(介质单位脉冲响应)q(t)。相应的,式(2)变为:

(5)
V(f)、S(f)、Q(f)可进一步分解为:
(6)

将式(6)代入式(5)可得:
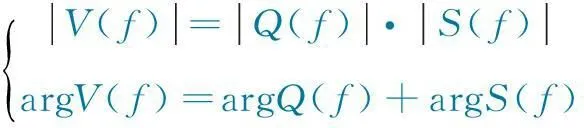
(7)
3.2震源激励函数
对于同一次夯击,不同测点i,j对应有各自不同的介质作用谱Qi(f)和Qj(f),但所对应的激励是相同的。比较测点i和j上的介质响应谱Vi(f)和Vj(f),代入式(4)得:
(8)
将式(6)代入上式可进一步得:
(9)
argQi(f)-argQj(f)=argVi(f)-argVj(f)
(10)
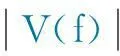
(11)
上式代入式(9)得:
(12)
特别地,当测点j位于强夯作用的塑性区与弹性区分界上时,令rj=r0,为弹、塑性区分界至强夯作用中心点的距离,此测点上对应的介质作用谱成为Q0(f);再令ri=r>r0,对应有Qi(f)=Q(f),代入式(12)得:
(13)
可以认为,当rj=r0时,有Vj(f)=S(f);而ri=r>r0对应有Vi(f)=V(f),代入式(10)并考虑式(13)的关系,得:
(14)
另外,由式(10)得:
argQ(f)-argQ0(f)=argV(f)-argS(f)
(15)
按波传播的概念,频率为f的波动以速度VR(f) 从r0传播到r时的相位变化为相应两个测点上介质作用谱的相位差,即:
(16)
将式(16)代入式(15)得:
(17)
(18)
其离散形式为:
(19)
式中,j=0, 1, …,n-1,n为测点振动时程的采样点数;fj=j/(n·t),t为测点振动波形的采样时间间隔(步长),应满足采样定理;时间t=j·t,0≤t≤T,T=n·t(采样长度)[5]。
如果考虑现场触发换能器与振源有一定的距离,以及线路延迟等因素所导致的仪器采样触发的滞后效应,则式(17)所示的相位函数成为:
(20)
式中,τ为触发滞后时间。以上各式中的波速VR(f) 为对应于频率f的相速度,可取为场地土体的瑞雷波波速度。
这样,根据现场测点上的强夯振动监测记录分析得到的强夯振动速度振幅谱|V(f)|和相位谱argV(f),即可由式(14)和式(17)或式(20)得到强夯震源的傅氏谱,进一步按式(18)或其离散形式,式(19),即可得到强夯震源振动的时程s(t)。
按上述强夯振动频域分析方法,根据测点监测得到的强夯振动数据,反演得到夯点土体振动时程,取得夯点振动特征参数(譬如,时域最大振速vm、卓越频率fm等),建立这些参数与夯点土体对应夯实加固状态的关系,这样,就解决了强夯加固状态振动实时监测研究的技术关键问题。
4夯点土体振动参数与土体加固状态之间关系的理论基础
运用强夯振动频域分析理论,可以利用观测点的强夯振动反演得到夯点土体的振动过程。夯点土体的振动主要是在夯锤的冲击方向上,可概化为一维土体振动。根据一维振动理论,可以定性认识夯点土体振动与夯点土体夯实程度之间的本质联系,为夯点土体加固状态的实时振动监测技术研发提供理论基础。
4.1夯点锤土复合体振动模型
如图4所示,设锤土复合体的质量为m,把地基土体对锤土复合体的支撑简化为弹簧和减震器的作用,分别用弹簧系数k和阻尼系数c描述。同时限定系统的运动沿z轴方向。锤土复合体的振动看作是具有初始速度v0、初始位移为零的单自由度自由振动。
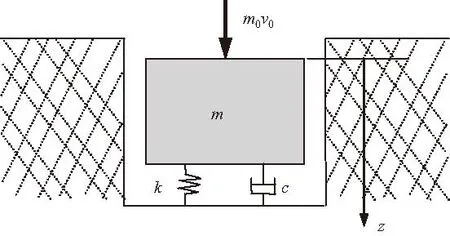
图4 夯点单自由度受迫振动模型
4.2夯点锤土复合体振动方程
按照牛顿第二定律F=ma研究系统的运动:
Fz=maz
(21)
式中,Fz为锤土复合体在z轴方向所受的合力,az为锤土复合体沿z轴方向运动的加速度。
设锤土复合振动系统的位移为z=z(t),则锤土复合体的加速度可以表示成:
(22)
根据以上的讨论,锤土复合体所受到的弹簧力Fk和阻尼力Fc分别为:
(23)
(24)
综合式(23)和式(24),得到系统在z方向所受到的合力Fz为:
(25)
把式(22)和(25)代入(21)整理得:
mz″+cz′+kz=0
(26)
式(26)即为锤土复合体的振动方程。
4.3夯点锤土复合体振动解
设方程(26)的解为以下形式:
(27)
式中,t为时间,λ为方程(26)的特征根,A为待定的常数。把式(27)代入式(26)整理得:
(28)
上式称为振动方程(26)的特征方程,求解得:
(29)
定义系统的阻尼比ξ如下:
(30)

(31)

即:
(32)
利用欧拉公式有:
eiωdt=cosωdt+isinωdt
e-iωdt=cosωdt-isinωdt
(33)
将公式(33)代入(32)式整理得:
(34)
对上式求导,得:
(35)
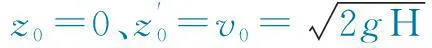
(36)
考虑夯点土体质量m=ρV=ρ0DV,其中D为土体的压实度,V为土体的体积,把阻尼比ξ表达式(30)和压实度D表达式D=ρ/ρ0代入阻尼振动圆频率的表达式,整理变形可得:
(37)
式(37)代入式(36)中的第一式,有:
(38)
从表达式(37)和式(38)可以看出,夯点土体的振动频率ωd和振幅A都和土体的压实程度D存在特定的关系,因此通过夯点的振动参数来反演土体的加固状态在理论上是有根据的。
5结语
文章提出了利用测点强夯振动反演夯点土体振动的思路,通过夯点锤土复合体体模型的建立,分析了加固状态间的物理联系,实现了对强夯施工中夯点土体加固状态进行实时监测。
参考文献
[1]张豫川,李彬.湿陷性黄土场地强夯夯沉量的预测[J].路基工程,2011(1):67-69,73.
[2]谭捍华,孙进忠,祁生文.强夯振动衰减规律的研究[J].工程勘察,2001(5):11-14.
[3]杨桂通.土动力学[M].北京:中国建材工业出版社,2000.
[4]孙进忠,谭捍华,祁生文,慎乃齐.影响强夯地面振动衰减的因素分析[J].现代地质,2000,14(2):230-234.
[5]郑治真.波谱分析基础[M].北京:地震出版社,1983.
中图分类号:TV522
文献标志码:B
文章编号:1005-4774(2015)04-0039-05
Study of dynamic compaction consolidation state real-time
monitoring method
LI Jinliang
(HebeiWaterConservancyBureau,Shijiazhuang050021,China)
Abstract:In the paper, dynamic effect of tamping hammer power effect on tamped soil is described. On the basis, a series of power process and effect in the deceleration movement process of tamping hammer from certain height to the ground are described, and dynamic compaction vibration transmission and attenuation rules are described. Theory of dynamic compaction vibration frequency domain analysis is systematically described, vibration model of hammer soil complex on the compaction point is established, and physical contact between compaction point soil vibration features and compaction point soil consolidation state is analyzed. Real-time vibration monitoring of ground foundation dynamic compaction consolidation state is realized.
Key words:dynamic compaction consolidation; vibration frequency domain; monitoring methods

