双层复合管液压胀接成形影响因素分析

徐龙江，雷君相，高贵杰，孙丹阳

（1.上海理工大学 机械工程学院，上海 200093；2.上海理工大学 材料科学与工程学院，上海 200093）

0 引言

双层复合管由不同金属材料的内层管和外层管组成，内外管之间紧密结合，在受力的作用下，内外管同时变形。双层复合管由于具备两种材料特性，在输送液体过程中能满足腐蚀性强、磨损大及温度高等特殊环境要求［1］，因此广泛应用于石油、化工、核电及机械制造等领域。

提高复合管之间的残余接触压力是研究复合管液压胀接成形方法的关键［2－3］。影响胀接残余接触压力的因素很多，本文将根据弹塑性理论［4］推导出残余接触压力计算公式，并分析内外管材料弹性模量、内外管之间初始间隙以及液压力对内外管之间残余接触压力的影响，为双层复合管材料、尺寸选择以及相关工艺参数的选择提供理论依据，对液压胀管具有重要的工程意义及参考价值。

1 液压胀接成形基本原理

双层复合管结构［5］如图1所示。内外层管均为厚壁管，内外管材料不同，胀接前内、外管之间存在间隙。液压胀接过程分为如下3个阶段：①将内管放入外管并置于相应模具内，对内管内壁加载液压力，直至内管外壁与外管内壁相接触；②持续对内管内壁加载，直至达到最大胀形量，完成保压过程；③对内管内壁卸载液压力，直至胀管液压力为零，内外管之间存在残余接触压力。

2 双层复合管液压胀接弹塑性力学分析

2.1 基本假设

基本假设如下：

（1）内层管将发生较大的塑性变形，应考虑材料的强化，假设内层管为线弹性强化材料模型；而外层管只发生弹性变形，将外层管设定为理想弹塑性线性材料模型。

（2）内外管均按厚壁管处理，由于管材较长，轴向应变很小，所以将内外管的变形过程简化为平面应变问题［6］。

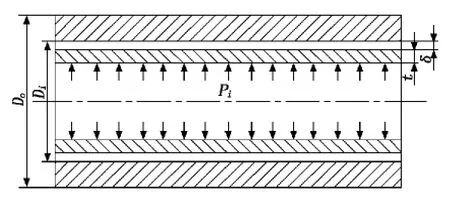
图1 双层复合管结构图

2.2 内层管胀形阶段应力分析

由于内外管间存在一定间隙，当内层管的外壁与外层管的内壁刚要接触时，内层管已发生较大的塑性变形而进入全面屈服阶段，忽略较小的弹性应变，此时内层管内的应力近似为：

其中：σ′si、σsi、E′i、Δε分别为内层管材料的应变强化应力、屈服强度、线性强化模量、塑性变形量；δ为内外管初始间隙；Ri为外管内半径。分析时认为σ′si在液压胀接过程中保持不变。

2.3 复合管胀接过程中应力应变分析

在内外管接触之前，内外管之间的接触压力为0，随着内层管内液压力的增加，内层管发生塑性变形并与外层管接触，并产生接触压力Pc，内层管受到管内液压力Pi和管外接触压力Pc的作用，处于平衡状态。按照塑性理论，依据Von Mises屈服准则，内层管外壁面的应力状态为：

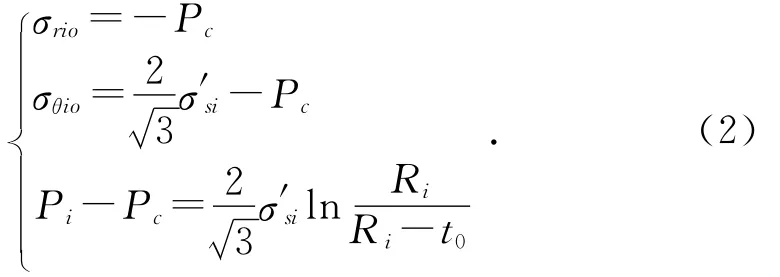
其中：σrio、σθio分别为内层管外壁面的径向应力和周向应力；t0为胀形后内管壁厚。

根据广义虎克定律，内层管外壁的周向弹性应变为：

其中：Ei、μi分别为内层管材料弹性模量、泊松比。

其中：σroi、σθoi分别为外层管内壁面的径向应力和周向应力。

根据广义虎克定律，外层管内壁的周向弹性应变为：

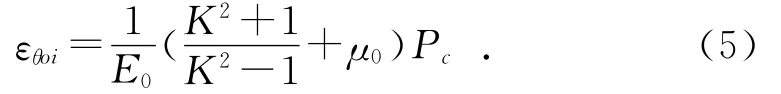
其中：E0、μ0分别为外层管材料弹性模量和泊松比。

2.4 复合管胀接成形后应力应变分析

当内层管内液压力卸载后，即Pi＝0，内外管相互接触，内外管之间存在一定的残余接触压力。由于残余接触压力P＊c的作用，内外层管处于弹性结合状态，根据拉梅尔公式，此时内层管外壁面的应力为：

根据广义虎克定律，内层管外壁处由产生的周向弹性应变为：

外层管内壁处由产生的周向弹性应变为：

2.5 复合管胀接成形后内外管之间的残余接触压力

设胀接成形前、后内层管的壁厚分别为t和t0，胀管前内外管之间的初始间隙为δ，则根据体积不变原理，求得t与t0的关系为：

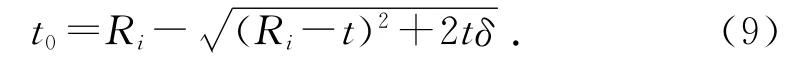
复合管液压胀接成形过程中变性协调条件为：

将式（3）、式（5）、式（7）、式（8）、式（9）代入式（10），并整理，可得复合管液压胀接成形液压力Pi与内外管间残余接触压力之间的关系式为：

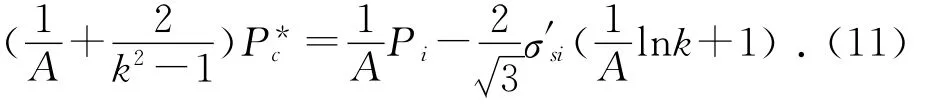
2.6 液压胀接成形液压力取值范围

双层复合管液压胀接成形后内外管相互接触，若内外管之间存在一定的残余接触压力，则≥0，由式（11）可求出最小液压力为：

在一定范围内残余接触压力随液压力Pi的增加而增大，但外层管的弹性变形是有限的，当外层管内壁开始屈服时，其弹性变形达到最大。外层管内壁开始屈服时接触压力Pc为：

其中：σso为外层管材料屈服强度。

将式（13）代入式（11），得出外层管只发生弹性变形时的最大液压力Pimax为：

3 复合管液压胀接成形影响因素

3.1 液压力对胀接成形的影响

根据成形液压力Pi与残余接触压力的关系式（11），当内外管材料、内外管的初始几何尺寸和形状不变时，若适当增加成形液压力Pi，内外管之间的残余接触压力会相应的增大。即在一定范围内，残余接触压力随成形液压力Pi的增加而增大。

3.2 弹性模量对液压胀接成形的影响

3.3 内外管初始间隙对液压胀接成形的影响

将式（1）代入式（11），当外层管几何尺寸及内外管材料一定时，A为一恒定常数，lnk≈0，所以：

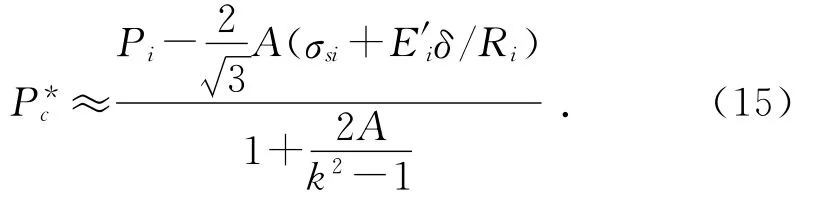
当增加液压胀接前内外管之间的间隙δ时，k增大，式（15）右侧分子变小，分母变大，变小，即残余接触压力随内外管初始间隙的增加而减小。

4 结论

（1）通过双层复合管的材料模型及力学模型假设，推导出外层管只发生弹性变形条件下的残余接触压力与液压胀接成形液压力Pi之间的理论计算关系式。

（2）在最大与最小成形液压力作用范围内，残余接触压力随成形液压力Pi的增加而增大。

（3）在一定范围内，残余接触压力随着内外管弹性模量比值的增加而增大，随着内外管之间初始间隙的增加而减小。

［1］吴凤梧.国外双金属管生产发展现状［J］.钢管，1996（3）：56－62.

［2］Fujun Liu，Jinyang Zheng，Ping Xu，et al.Forming mechanism of double－layered tubes by internal hydraulic expansion［J］.International Journal of Pressure Vessels and Piping，2004，81：625－633.

［3］颜惠庚，张炳生，葛乐通，等.换热器的液压胀管研究（二）——残余接触压力与摩擦系数［J］.压力容器，1996，13（4）：39－43.

［4］余同希.塑性力学［M］.北京：高等教育出版社，1989.

［5］王学生，李培宁，王如竹.双金属复合管液压成形压力的计算［J］.机械强度，2002，24（3）：439－442.

［6］范钦瑚.轴对称应力分析［M］.北京：高等教育出版社，1985.

［7］徐芝纶.弹性力学［M］.北京：高等教育出版社，1998.