退化抛物-双曲型方程柯西问题的解关于初值的连续性*
郝兴文
(潍坊学院,山东 潍坊 261061)
1 问题与主要结果
考虑下列退化抛物-双曲型方程的柯西问题:


由于这个方程的应用广泛,大家对它的研究也由来已久。这个方程在某些方向上抛物退化,所以他的解显示出双曲方程的一些性质,解会出现间断。Volpert-Hugjaev在文献[8]中最先给出了方程(1)的BV 解的存在性,Chen-Karlsen在文献[10]证明了解的唯一性。另外,Chen-Perthame在文献[4]中得到了方程(1)中系数不显含x,t形式的齐次方程动力学解的存在唯一性,其它形式的解可以见文献[5,6,7,9]等。对于系数不显含x,t的方程,它的解在初始时刻具有连续性,从而说明初始层不会出现,参见文献[4],特别是对于完全退化的情形—双曲型方程,这个性质在文献[11]中应用双变量方法给予了证明。对于一般形式的方程(1),解的这个性质是否成立没有结果。本文将主要证明方程(1)-(2)的解具有这个性质。首先引入本文中要用到的一些记号和方程(1)-(2)的解的定义。记

对任意的非负φ∈C(R),令

记R2上的动力学函数[4]为

问题(1)-(2)的动力学解定义为
定义1 一个可测函数u∈L∞([0,T]),L1(Rn+1))是方程(1)的动力学解,如果u满足
(ii)对任意两个非负函数φ1,φ2∈C(R),下式成立

(iii)对某个非负测度m,下式在D′([0,T)×Rn)中成立

其中,测度n由下式给出
本文的主要结果是
定理1 如果初值u0(x)∈L1(Rn)∩L∞(Rn),u 是(1)—(2)的动力学解,则当t→0时,有‖u(·,t)-u0(·)‖L1(Rn)→0。
2 定理的证明
首先引入一个引理,设函数g(ξ)满足

下列引理成立:
引理1 设函数g(ξ)满足上面的条件,如果存在数u和非负可测函数~m(ξ)∈C0(R)满足

该引理的证明可参见文献[12],细节省略。




令Ri→+∞后,利用m 和n 的非负性,得


所以

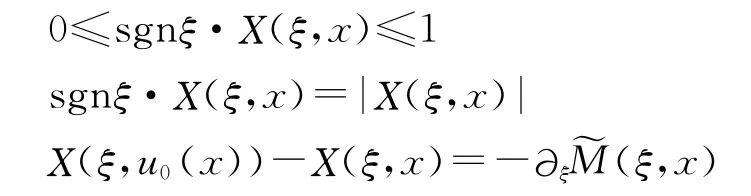
首先,对任意的E∈Rn,且m(E)<+∞,则

所以,0≤sngξ·Χ(ξ,x)≤1,且sngξ·Χ(ξ,x)=|Χ(ξ,x)|。
另一方面,


令τ→0,得到,

特别地,对任意的τ>0,选取实验函数ω(ξ,t,x)=φ(ξ,x)ψ(t),其中,
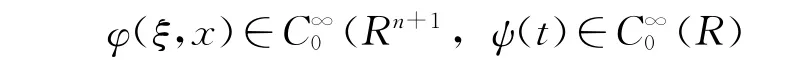

在分布意义下,


在上面引理的基础上,给出定理1的证明

由极限的唯一性可知
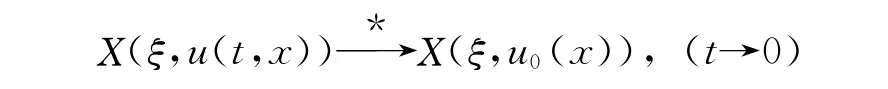
在(4)中,令τ→0,可得
由σ的凸性及u(t,x)弱收敛到u0(x),表明该收敛是强收敛,从而定理1成立。
[1]Juan L V.The porous medium equation:mathematical theory[M].London:Oxford university press,2006.
[2]Bustos M C,Concha F,Bürger R,et al.Sedimentation and Thicking:Phenomenological Foundation and Mathematical Theory[M].Dordrecht Netherlands:Kluwer Academic Publishers,1999.
[3]Antonelli F,Barucci E,Mancino M E.A comparison result for FBSDE with applications to decisions theory[J].Math Meth Oper Res,2001,(54):407-423.
[4]Chen G Q,Perthame B.Well-posedness for non-isotropic degenerate parabolic-hyperbolic equation[J].Analyse nonlineaire,2003,(20):645-668.
[5]Carrillo J.Entropy solutions for nonlinear degenerate problems[J].Arch Rational Mech Anal,1999,(147):269-361.
[6]Bendahmane M,Karlsen K H.Renormalized entropy solutions for quasilinear anisotropic degenerate parabolic equations[J].SIAM J Math Anal,2004,(36):405-422.
[7]Perthame B,Souganidis P E.Dissipative and Entropy Solutions to Non-Isotropic Degenerate Parabolic Balance Laws[J].Arch Rational Mech Anal,2003,170(4):359-370.
[8]Volpert A I,Hugjaev S I.Cauchy’s problem for degenerate second order quasilinear parabolic equation[J].Transl Math USSR Sb,1969,(7):365-387.
[9]Wu Z,Zhao J,Yin J,et al.Nonlinear diffusion equation[M].Chennai:World Scientific publishing,2001.
[10]Chen G-Q,Karlsen K.Quasilinear anisotropic degenerate parabolic equations with time-space dependent diffusion coefficients[J].Commun Pure Appl Anal,2005,4(2):241-266.
[11]Eymard R,Gallout T,Herbin R.Existence and uniqueness of the entropy solution to nonlinear hyperbolic equation[J].Chin Ann Math,1995,(16):1-14.
[12]Perthame B.Kinetic formulation of conservation laws[M].Oxford university press,2002.

