基于最大化信噪比的大规模MIMO预编码算法

武宇花

（西安邮电大学信息与通信工程学院 西安 710061）

1 引言

2010年底，贝尔实验室科学家Marzetta T L提出了大规模多天线系统的概念，即massive MIMO或者large scale MIMO(大规模MIMO)，大规模MIMO是一项新型的通信技术，它通过在基站侧配置很多天线阵列，进而为单天线终端提供多样性。它还可以极大地提高频谱效率和能量效率[1]。按照香农公式，如果基站天线数目趋于无穷，则信道容量就无限大。但在实际中这并不成立。这是因为随着天线数目增加，系统硬件复杂度就会增加，信道状态信息也难以获得；此外一个很重要的因素就是导频污染。有关大规模MIMO系统的概述见参考文献[2,3]。

现阶段无线通信技术要求更高的传输速率，这就促进了对数据处理手段的研究，预编码技术就在此时应运而生，预编码技术是一种需要在发送端已知信道状态信息的情况下对数据进行处理的技术。大规模MIMO系统中的预编码技术的主要目的是提高天线阵列增益和消除导频污染。参考文献[4]提出了一种新颖的基于MMSE的预编码，它可以有效消除导频污染。参考文献[5]证明了预编码可以减少小区间干扰并且通过转换相邻小区时间帧中导频的位置获得更好的信道估计。在参考文献[6]中，基站把来自不同小区复用相同导频的终端信息线性结合，此外，每个基站独立地发送它们基于慢衰落系数的预编码矩阵。

用(·)H表示共轭转置，(·)-1表示矩阵的逆阵，E{·}代表期望,x～CN(μ,σ2)表示x是均值为 μ、方差为σ2的高斯变量，I表示单位矩阵。

2 系统模型

假设系统模型中有L个六边形小区，每个小区有一个基站，每个基站配置M根天线，服务K个单天线用户，这里假设M小于或等于K。如图1所示，基站在发送给用户数据之前先采用线性预编码来处理发送数据，这就需要基站侧知道信道状态信息。之前所做的研究大部分是在FDD系统中，其中的信道状态信息是通过有限反馈得到的，有很多文献致力于设计反馈机制的预编码策略，以使MIMO下行链路的吞吐量达到最大化[7～10]。本文的目的是设计获得将其应用于多小区MIMO TDD系统的预编码方案。系统采用的是TDD模型，因此基站可以利用信道互易性来获得信道状态信息，即上行链路和下行链路的信道矩阵几乎是相等的。信道状态信息的估计可以从上行训练序列中估计获得。此外假设在一个相干时间间隔内信道情况是保持不变的。

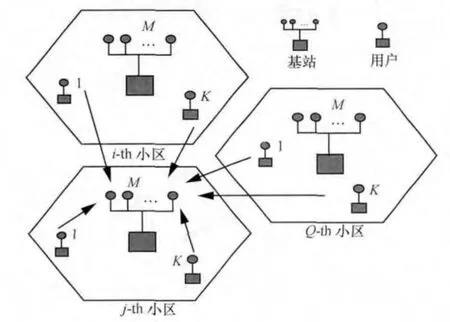
图1 大规模MIMO系统示意

3 基于信道估计的预编码

在这部分将提出一种新的基于上行信道估计的预编码方式，它的目的是实现接收端信噪比的最大化，在每个相干时间间隔中，分为以下3个步骤：首先，每个用户给基站上行发送长度为τu的导频数据,基站通过接收到的导频序列进行MMSE信道估计；然后基站基于得到的信道状态信息，在发送下行数据之前对数据进行预编码处理；最后接收端依据最大化信噪比来获得预编码矩阵A基于上行导频训练的信道估计。

（1）上行发送数据

设τu为每个相干时间内的导频符号数，所有用户同时发送长度为τu的导频符号，ρu为上行导频符号的平均发送功率，K个用户的导频符号是相互正交的，这就要求τu大于或等于K。

假设H为基站和K个用户之间的信道矩阵，假设矩阵H中的每个分量是均值为0、方差为1的独立同分布高斯随机变量，在这里为了简化运算，忽略了大尺度衰落的影响，采用MMSE信道估计准则，得到H的估计值为[11]：

其中，Nu为服从N（0,1）的高斯矩阵，ρu为上行导频符号的平均发射功率。因为是通过信道估计得到的信道状态信息，因此肯定会存在估计误差，这样真实信道就可以写为估计信道与误差信道之和。因此真实的信道可以分解如下：

（2）下行发送数据

考虑有Nt根发射天线、Nr根接收天线的MIMO系统，将数据分成Nt个子数据流，每个子数据流通过星座点映射后送给发射天线。集中讨论确定性的窄带时不变的信道，每个收发端天线对的衰落是平坦的。在这个模型下，在第i个符号时间的接收信号可以写为：

Si是在时刻i发送的nT×1维的信号，Hi是i时刻的nR×nT维的信道矩阵，N=（n1，n2，…,）是各分量相互独立且都服从N（0，σn2）分布的高斯噪声。

（3）基于信道估计的预编码

基站在下行发送数据之前先对数据进行预编码，设下行发送的数据为d，在第i时刻发送的信号的方差为E{|di|2}=，假设接收端经历同样的衰落，基站在对下行数据进行预编码的预编码矩阵表示为w，那么发送信号就可以表示为s=wd，在i时刻的接收信号为[13]：

则信噪比的表达式可以写为：

约分公因式之后得到：

很明显，在通信系统中追求高信噪比，接下来求预编码矩阵的过程就转化为下面的问题[14]。

这是著名的瑞利熵优化问题，即需要计算出最大特征值对应的特征向量，式（7）的最优向量为[15,16]:

至此已经找到了最优的预编码向量和对应的信噪比表达式，从中可以看出，预编码矩阵与信道估计误差的期望、估计信道和噪声方差和数据方差之比有关，由此可以看出，某一时刻发送端预编码矩阵与该时刻信道的统计特性密切相关。下面将对该算法进行性能仿真及比较。

4 仿真结果

在本节中提供了一些仿真结果来评估该算法的性能，其中表1给了几个关键仿真参数。

表1 仿真参数

目前普遍使用的预编码方法是基于SVD分解的，当然也有一些基本的算法，包括MF预编码方法、MRT预编码方法和非线性预编码方法。对本文算法与SVD预编码算法进行了比较，图2给出了当发射天线数为50时两种算法误码率随信噪比的变化趋势，图3给出了当发射天线数为500时两种算法误码率随信噪比的变化趋势。可以看出，该算法的性能高于SVD预编码算法的性能，且当天线数越大时本文算法的优势越明显。究其原因是基于SVD的预编码方法需要对信道进行SVD分解，代价是增加了计算复杂性和能源消耗，尤其当发射天线数大、信道矩阵阶数高时。本文算法在计算预编码矩阵时不必进行信道分解，可以从信道的统计特性中得到，减轻了硬件设备的负担，因此可以提高效率。

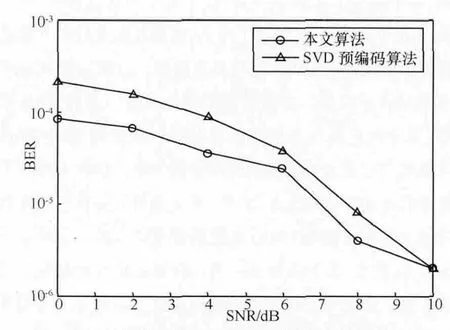
图2 发射天线Nt=50时两种算法性能比较

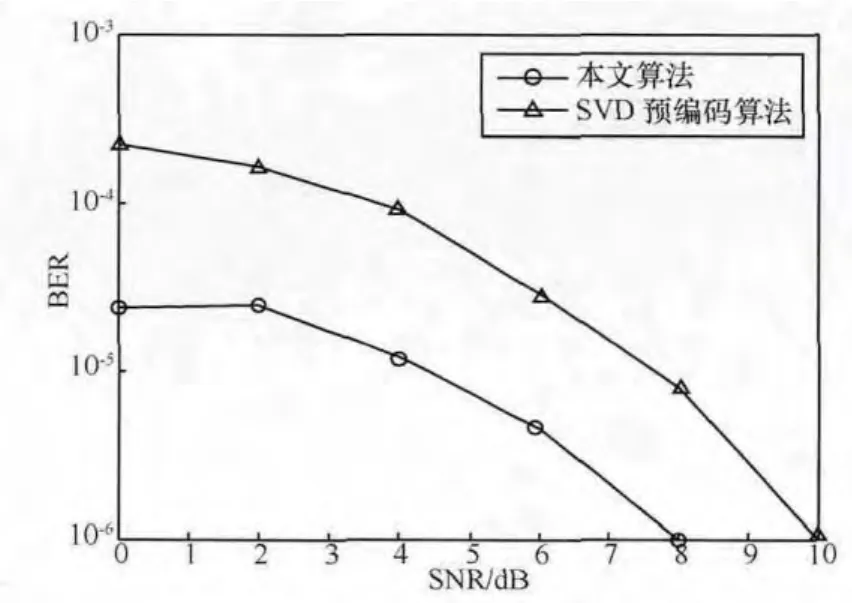
图3 发射天线Nt=500时两种算法性能比较

5 结束语

通过上面的仿真可以看出，当发射天线数大的时候，信道矩阵也变得庞大，此时SVD信道分解方法将变得复杂，宜采用本文的预编码算法。

本文在信道方面做的工作主要是信道估计和信道估计误差，并且一开始假设在一个相干时间间隔内信道是不变的。在实际的大规模MIMO系统中有必要考虑一些实际因素，例如信道是受建筑群、地形、地貌的影响而随时变化的，因此研究信道变化及信道预测变得很有价值。一些相关的文献结果见参考文献[17]。未来的工作可以研究一些以经典滤波器设计为基础的信道预测，以此来克服信道变化的影响。此外，还可以比较不同滤波器信道预测的效果。

1 Marzetta T L.Noncooperative cellular wireless with unlimited numbersofbase station antennas.IEEE Transactionson Wireless Communications,2010,9(11):3590～3600

2 Rusek F,Persson D,Lau B K,et al.Scaling up MIMO:opportunities and challenges with very large arrays.IEEE Signal Processing Magzine,2012,30(1):40～46

3 Lu L,Li G,Swindlehurst A,et al.An overview of massive MIMO:benefits and challenges.IEEE Journal of Selected Topics in Signal Processing,2014,8(5):742～758

4 Jose J,Ashikhminand A,Marzetta T L.Pilot contamination and precoding in multi-cell TDD systems.IEEE Transactions on Wireless Communications,2009,10(8):2640～2651

5 Appaiah K,Ashikhminand A,Marzetta T L.Pilot contamination reduction in multi-user TDD systems.Proceedings of the IEEE International Conference on Communications(ICC),Cape Town,South Africa,2010

6 Ashikhmin A,Marzetta T.Pilot contamination precoding in multi-cell large scale antenna system.Proceedings of the 2012 IEEE International Symposium on Information Theory,Cambridge,Massachusetts,USA,2012

7 Sharif M,Hassibi B.On the capacity of MIMO broadcast channels with partial side information.IEEE Transactions on Information Theory,2005,51(2):506～522

8 Ding P,Love D J,Zoltowski M D.On the sum rate of channel subspace feedback for multi-antenna broadcast channels.Proceedings of the IEEE Global Telecommunications Conference,San Antonio,Texas,USA,2005:2699～2703

9 Jindal N. MIMO broadcast channels with finite-rate feedback.IEEE Transactions on Information Theory,2006,52(11):5045～5060

10 Yoo T,JindalN,Goldsmith A.Multi-antenna broadcast channels with limited feedback and user selection.IEEE Journal Sel Areas Communications,2006,25(7):1478～1491

11 Sailes K,Sengijpta.Fundamentals of statistical signal processing:estimation theory.Technometrics,1995,37(4):465～466

12 Ngo H Q,Larsson E G,Marzetta T L.Massive MU-MIMO downlink TDD systems with linear precoding and downlink pilots.Proceedings of the 51st Annual Allerton Conference on Communication,Controland Computing,Allerton,England,2013:293～298

13 So J,Kim D,Lee Y.Pilot signal design for massive MIMO systems:a received signal-to-noise-ratio-based approach.IEEE Signal Processing Letters,2014,22(5):549～553

14 Bogale T E,Le L B.Pilot optimization and channel estimation for multiuser massive MIMO systems.Proceedings of the 48th Annual Conference on Information Sciences and Systems(CISS),Princeton,NJ,USA,2014:1～6

15 Boyd S,Vandenberghe L.Convex Optimization.London:Cambridge University Press,2004

16 Bogale T E,Vandendorpe L.Max-min SNR signal energy based spectrum sensing algorithms for cognitive radio networks with noisevariance uncertainty.IEEE Transactionson Wireless Communications,2014,13(1):280～290

17 Heath R W,Truong K T.Effects of channel aging in massive MIMO systems.Journal of Communications&Networks,2013,15(4):338～351