基于国库现金最佳持有量的国库现金管理探讨
基于国库现金最佳持有量的国库现金管理探讨
甘璐
(厦门市思明区国库支付中心,福建厦门361004)
[摘要]科学确定国库现金最佳持有量,是成功运作国库现金管理的关键。采用理论分析和实证研究相结合的方法,对比了目前常用的四种计算现金最佳持有量的模型,得出基于随机模型的国库最佳现金持有量模型。通过实际数据测算福建省某区2009—2013年国库现金最佳持有量及最佳持有区间,研究表明运用随机模型来计算国库现金最佳持有量是可行的,有利于提高预测的可操作性且管理起来更为灵活。
[关键词]国库现金;最佳持有量;随机模型
近年来,随着财政收入的增长和国库集中支付制度的不断发展,资金大量沉淀在国库,造成了资金的闲置浪费。2006年,中央级国库正式开展地方国库现金管理,并取得了显著成效。目前,各地开展地方国库现金管理的呼声也越来越高,实施地方国库现金管理成为发展的必然趋势。国库现金管理,就是要在确保国库现金开支需要的前提下,实现国库闲置资金最小化和收益最大化。因此,如何确定国库现金最佳持有量,是成功运作国库现金的关键。笔者以确定国库现金最佳持有量为基础,尝试提出测算最佳现金持有量的模型,并以福建省某区(简称X区)的数据为例进行测算(根据相关保密规定,数据都经过相应的处理),以期为基层国库现金管理研究带来借鉴作用。
一、计算最佳现金持有量的常用模型
国库现金最佳持有量,是指国库现金在央行国库账户上的“目标余额”,是一个适度规模的库存现金量。[1]这个“目标余额”不能过低,应满足政府日常的开支需要,从而避免现金短缺带来的损失,又不能过高,使得丧失利用国库现金投资获利的机会,造成资金浪费。因此,如何科学确定国库最佳现金持有量,既保证资金的安全又能缩减国库现金余额、最大化收益是开展国库现金管理的关键之一。
在市场经济环境下,国库应该成为一个独立的市场主体参与资本市场的现金管理和资本运作,因此,撇开国库形成的原因和权利来源的考虑,假设国库也是与普通公司平等的相对方,借鉴企业最佳现金持有量确定方法来进行计算。目前常用的方法有:成本分析模式、现金周转模型、存货模型、随机模型。[2]
(一)成本分析模式
成本分析模式通过研究持有现金所产生的成本,寻找成本最低时的现金持有量。成本分析模式仅考虑持有现金所产生的短缺成本及机会成本,并认为管理成本在一定的现金范围内与现金量关系不大,可以看作是固定的。短缺成本指由于现金短缺不能及时保证业务照常进行而遭受的损失,这部分现金与现金持有量负相关。机会成本指公司因持有一定现金而放弃的投资收益,通常按无风险利率进行计算,机会成本=现金量×利率。如图1所示:机会成本线向上,短缺成本线向下,管理成本线不变,总成本线形成一条抛物线,其底端就是持有现金产生的最低成本,这一点对应的量即最佳现金持有量。
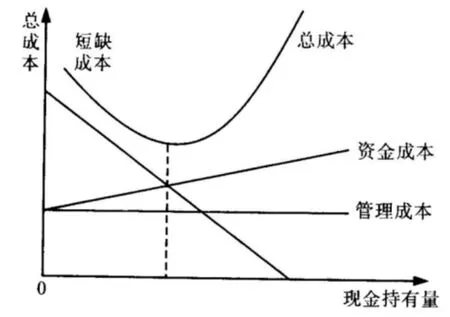
图1 成本分析模式示意图
(二)现金周转模型
现金周转模型充分考虑现金的周转,根据现金的周转速度来计算最佳现金持有量。流动资产被认为是与公司经营同时进行的一系列转换的完成。现金“变成”存货和劳动力,它们结合在一起就变成了产品。当产品出售时,产生应收账款,当收回时变成现金。这个过程即现金流的过程。如图2,现金周转期=存货周转期+应收账款周转期-应付账款周转期。从而得出现金周转率=360天/现金周转天数,在计算确定现金周转期和周转率后,就可以确定最佳现金持有量=预计年现金需求量/现金周转率。
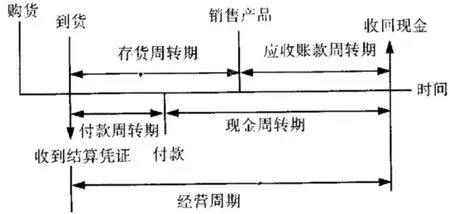
图2 现金周转示意图
(三)存货模型
存货模型又称Baumol模型,是美国财务学家William J·Baumol提出的。他认为公司的现金持有量与存货在许多方面相似,因此存货的经济批量模型可应用于确定现金持有量。这一模型的假设是: (1)在一个营运周期内,公司的现金流量是可以预测且均匀发生的; (2)不存在现金短缺,在公司持有现金为零时,公司可及时等额地补充现金,使现金持有量恢复到起点水平; (3)可变现有价证券来获取所需现金,且不确定性很小; (4)证券的利率及每次变现的交易成本可以获悉。
公司每次变现有价证券来取得现金所付出的代价即现金的交易成本,其与现金周转次数和每次转换量有关。假定交易成本不变,当现金持有量越高,有价证券转换为现金的次数就越少,转换总成本就越低,转换成本与现金持有量呈反比。但是,现金持有量越高,现金的机会成本就越高,这三者的关系如图3所示。
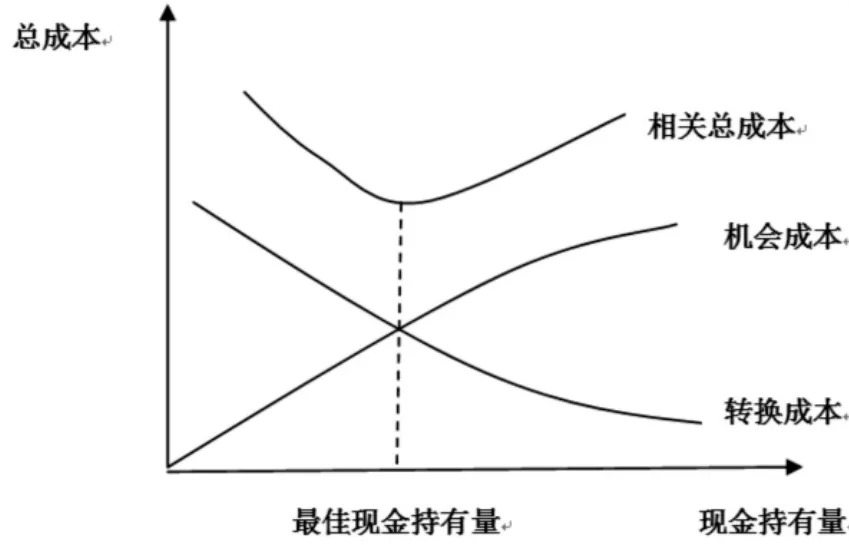
图3 存货模型示意图
设Q为现金持有量,有价证券利率(机会成本)为K,一定时期现金需求量为D,每次出售有价证券补充现金的转换成本为F,则总的转换成本为(D/Q)×F,持有现金的总成本=机会成本+转换成本= (Q/2)×K + (D/Q)×F。
存在最佳现金持有量Q*使得(Q*/2)×K = (D/Q*)×F时总成本最低,得出:最佳现金持有量Q*=。
(四)随机模型
随机模型又称Miller-Orr模型,是美国经济学家Merton Miller和Daniel Orr提出的。这个模型适用于测算现金流随机变动情况下的最佳持有量。这一模型的假设是: (1)现金流波动不可预测; (2)现金收支数量不规则,随机变动; (3)持有现金的成本是所损失的投资收益; (4)现金和有价证券可以互换。在这种情况下,首先根据历史数据和经验确定下限L,上限H超过下限3Z个单位,M为均衡点,是机会成本和交易成本博弈的结果,即最佳现金持有量。如图4所示,当国库现金余额达到上限,将2Z数额的现金投资于有价证券,使现金减少;反之低于下限时,将Z数额的有价证券售出,使现金回升,最终,持有的现金会在不断调整中趋向均衡点。
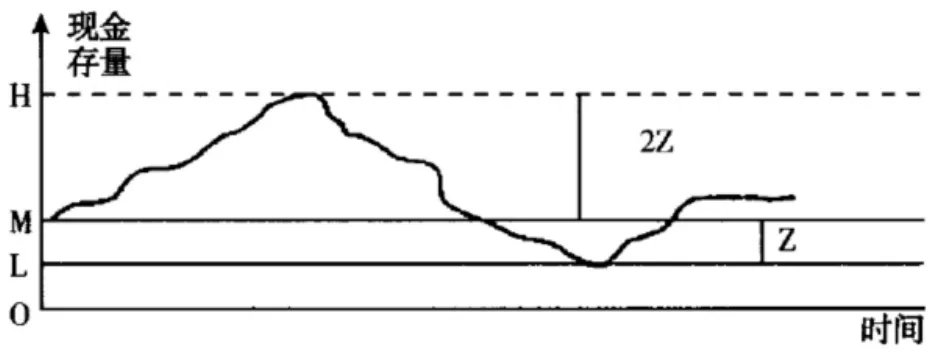
图4 随机模型示意图
设转换有价证券的固定成本为E,日现金净流量的标准差为σ,持有现金的机会成本为K,则Z =,最佳库存量M = Z + L,上限H =3Z + L。
二、模型的分析及选择
比较上述四个模型,得出以下各模型的优劣势:
成本分析模式:该模式考虑的是资金的短缺成本和机会成本,二者一旦确定,就比较容易求出最佳持有量,这种方法较直观,易于判断。但是在国库现金管理中,受国库支出突发性和临时性变动较多的影响,国库资金的短缺成本测算难度较大,因此这个模型在运用时难度较大。
现金周转模型:该模型考虑的是现金的周转情况,反映出国库现金的流入流出。但是,它的缺点是现金周期长短难以确定,各地区受技术条件、地理位置等的影响,国库支付清算手段相差较大,资金的周转天数各不相同,一旦周期不准确,直接影响到最终结果。
存货模型:该模型充分考虑了机会成本和转换成本,而且模型的计算具有可操作性。但是,该模型的假设条件过于苛刻,“公司的现金流量是可以预测且均匀发生的”这样的假设过于理想化,与国库现金流波动存在差异。
随机模型:该模型考虑了现金波动的随机性,对于频繁变动的国库资金而言是一个比较好的选择,且确定一个上下限的区间,管理起来较有灵活性。但是,根据经验来确定下限值具有主观性,容易产生较大偏差。模型中变量σ、K、E都是变动的,尤其是持有现金的机会成本K随着金融市场的变化随时变化,使得计算出的最佳现金持有量变动性较大。
综上所述,由于成本分析模式和现金周转模型的变量难以有效测算,存货模型的假设条件与国库现金流波动存在差异,暂不选择这三种模式。由于政府现金流波动的随机性符合随机模型的假设,且随机模型确定的最佳区间管理起来更有灵活性,尝试选择随机模型来计算国库现金最佳现金持有量。
三、X区国库现金最佳持有量的实证分析
笔者根据X区2009—2013年每个月的国库现金库存,运用随机变量模型来尝试算出该区的国库最佳现金持有量。受各地国库管理水平、计算机信息系统水平、金融市场完善程度等的限制,地方国库目前还没办法做到完全效仿发达国家将国库日余额控制在零的做法,而把分析放在国库月余额上较为可行。笔者以月为时间单位进行分析,具体如下:
(一)下限L的确定
为保证资金的安全,根据谨慎性的原则,选取每个月月余额最小值作为下限风险过大,而选取每个月支出数的最大值作为下限又未考虑到每个月都有收入的现金流入,过于稳健,因此结合收支来考虑,从净现金流的角度出发,根据国库每月的现金流入和流出量(见表1),将每个月现金流出减去每个月现金流入,得出表2,选取资金净流出最大月份的净流出额作为下限。如表2所示,2009年下限L为13 410万元,2010年L为26 733万元,2011年L为21 939万元; 2012年L 为31 327万元,2013年L为47 421万元。
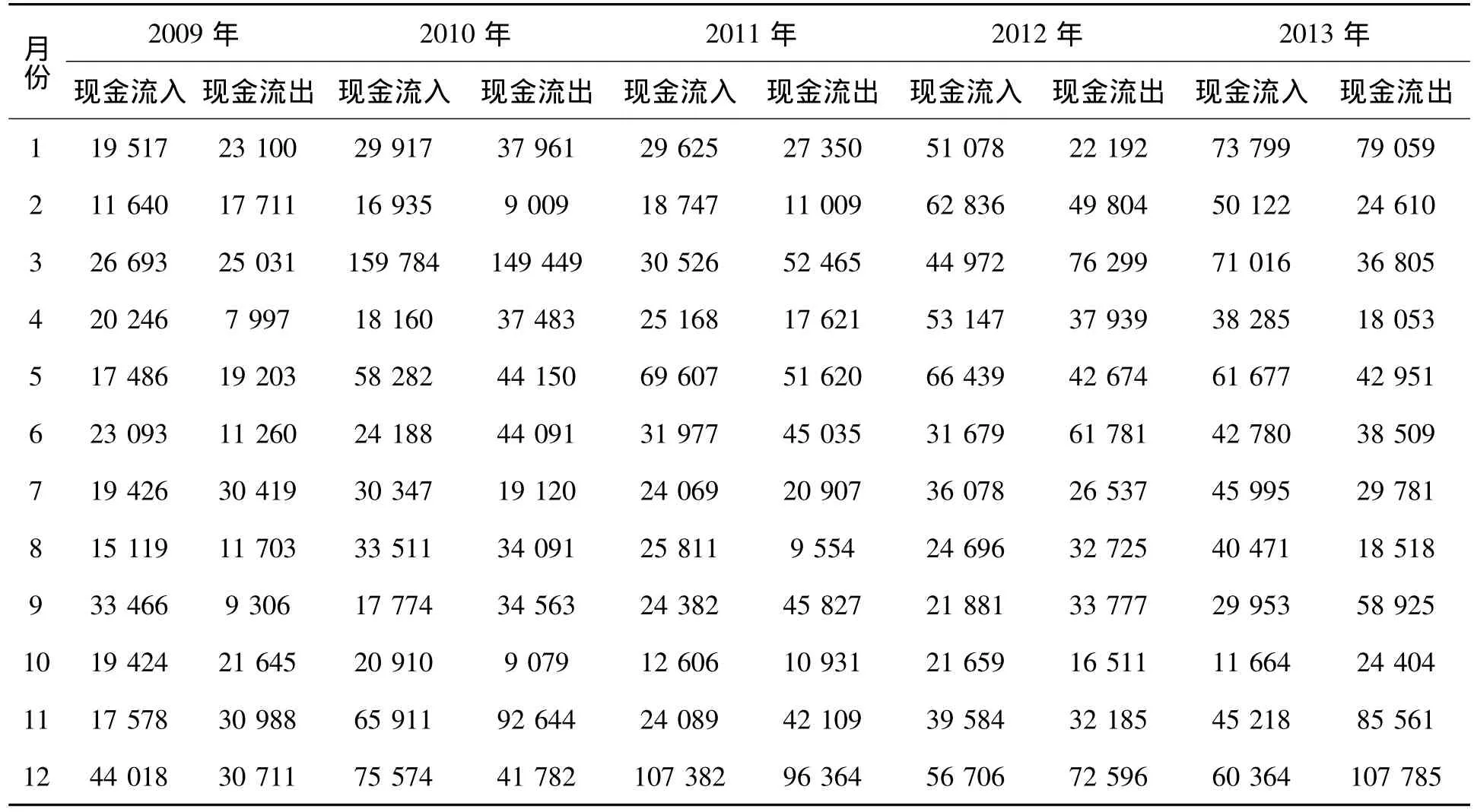
表1 2009—2013年国库现金流量表 单位:万元
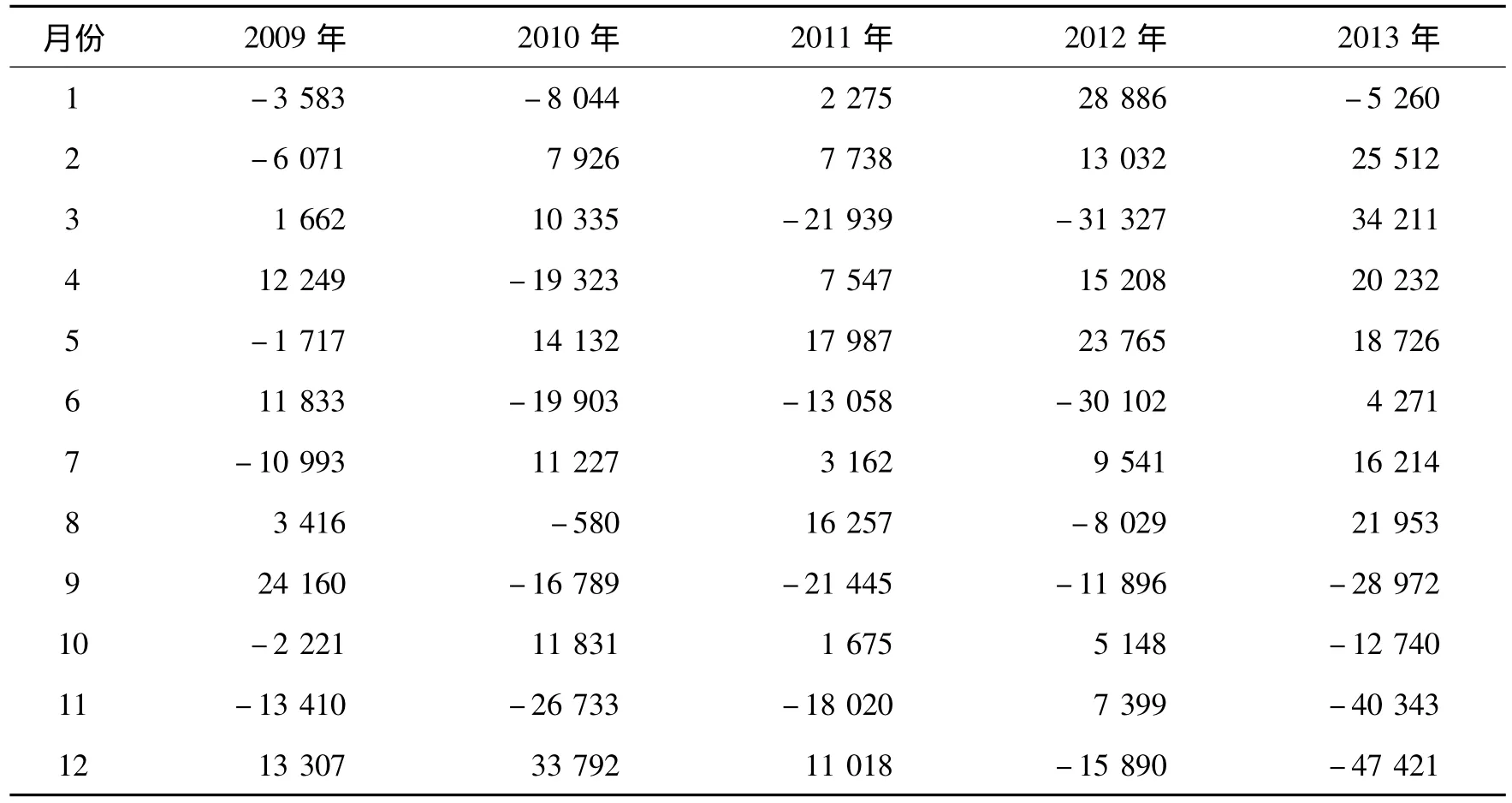
表2 2009—2013年国库现金净流量表①资金净流入为正,资金净流出为负。 单位:万元
(二)转换成本、机会成本、标准差的确定
1.转换成本E。尽管国库现金转换为商业银行存款的操作性最强,但是由于国库现金转换为定期存款、通知存款等基本不存在转换成本,因此,以下模型暂不考虑这种模式。由于国库资金的特殊性,国库现金的运作需保证资金的安全,尽可能地减少运作的风险。[3]考虑到质押式债券回购是相对较安全的金融工具,以下选取国库现金参与银行间质押式债券回购的单一投资模式。我国目前银行间质押式债券回购交易的品种主要有1天、7天、14天、21天、1个月,采取谨慎的做法,选取最高的交易频率,使得转换成本最高,从而计算出的最佳区间的上限最高。因此,在交易频率最高的情况下,每月完成上述回购22次(假设一个月22个工作日)、4次、2次、1次、1次,共计30次。按照银行间债券市场国债回购交易费用规定,单券种单笔回购交易费用为120元①中央国债登记结算有限责任公司业务收费办法,中债字[2005]56号文。,月回购交易成本共计3 600元。
2.机会成本K。由于选取了国库现金参与质押式债券回购的单一投资模式,因此机会成本相应就是质押式债券回购的年利率。根据2009—2013年《全国银行间市场债券回购交易期限分类统计表》,将投资占比作为权重,计算出加权平均年利率。如表3所示,2009年加权平均年利率= 78.11%×1.01% + 15.43%× 1.27% + 4.86%×1.23% + 0.97%×1.27% + 0.62%×1.31% =1.065 2%,则2009年加权平均月利率K = 1.065 2% /12 = 0.088 8%。同理,2010年K =1.818 6% /12 =0.151 6%; 2011年K = 3.442 2% /12 = 0.286 9%; 2012年K = 2.896 1% /12 =0.241 3%; 2013年K =3.521 4% / 12 =0.293 5%。
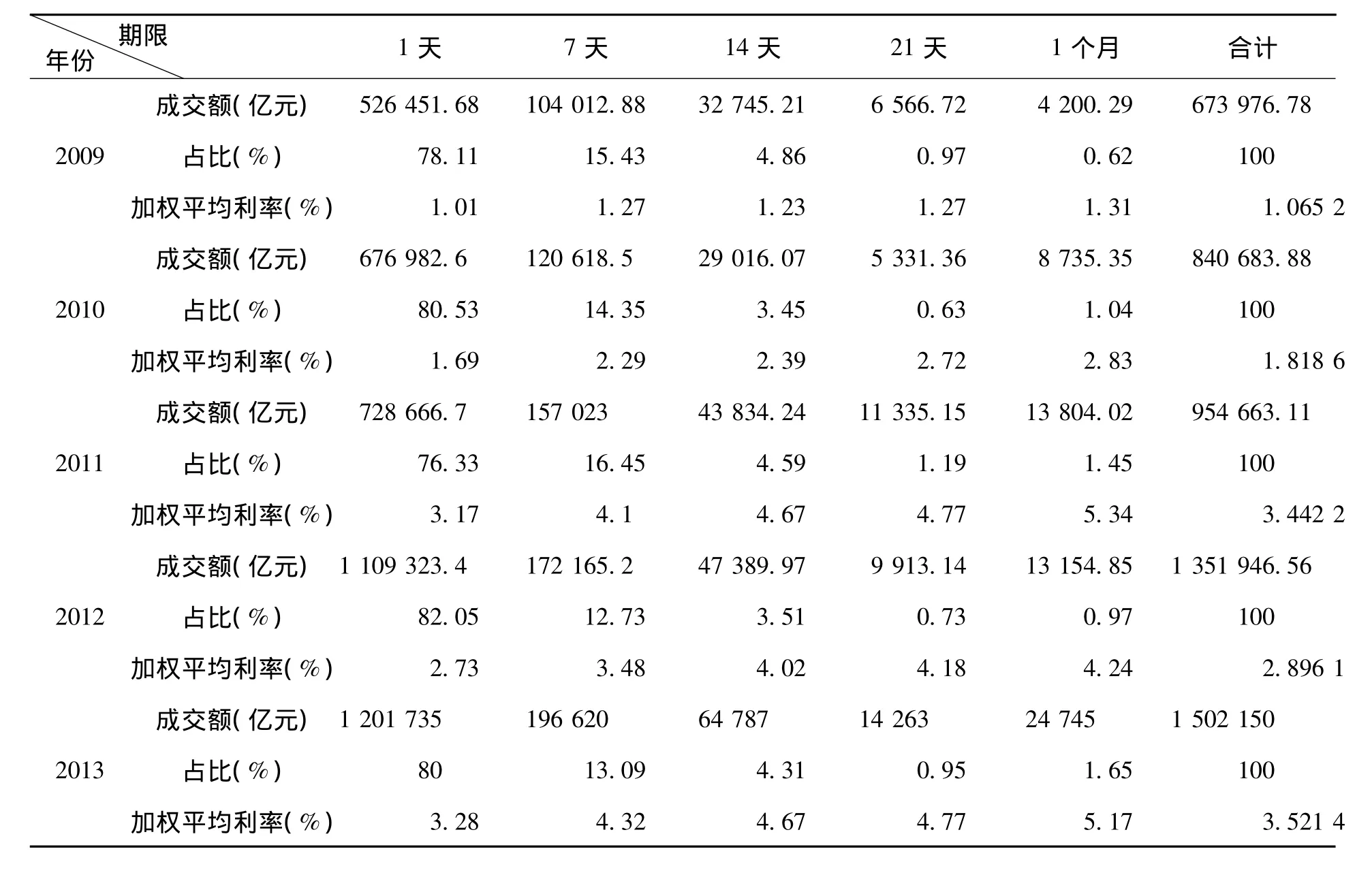
表3 2009—2013年全国银行间市场债权回购交易分类统计表②中国人民银行网站,统计数据与标准。
3.标准差σ。根据2009—2013年每月的国库现金余额计算得出2009年标准差σ为14 202万元,2010年标准差σ为12 171万元,2011年标准差σ为10 556万元,2012年标准差σ为13 085万元,2013年标准差σ为42 125万元。
(三)最佳现金持有量的确定
将转换成本E、机会成本K、标准差σ代入公式,2009年Z == 3 926万元,2010年Z =2 971万元,2011年Z =2 187万元,2012年Z =2 671万元,2013年Z =5 714万元。如表4所示,2009年国库最佳库存量M = Z + L =17 336万元,国库现金持有量的上限H =3Z + L =25 188万元,2010年M为29 704万元,H为35 646万元,2011年M为24 126万元,H为28 500万元,2012年M为33 998万元,H为39 340万元,2013年M为53 135万元,H为64 563万元。
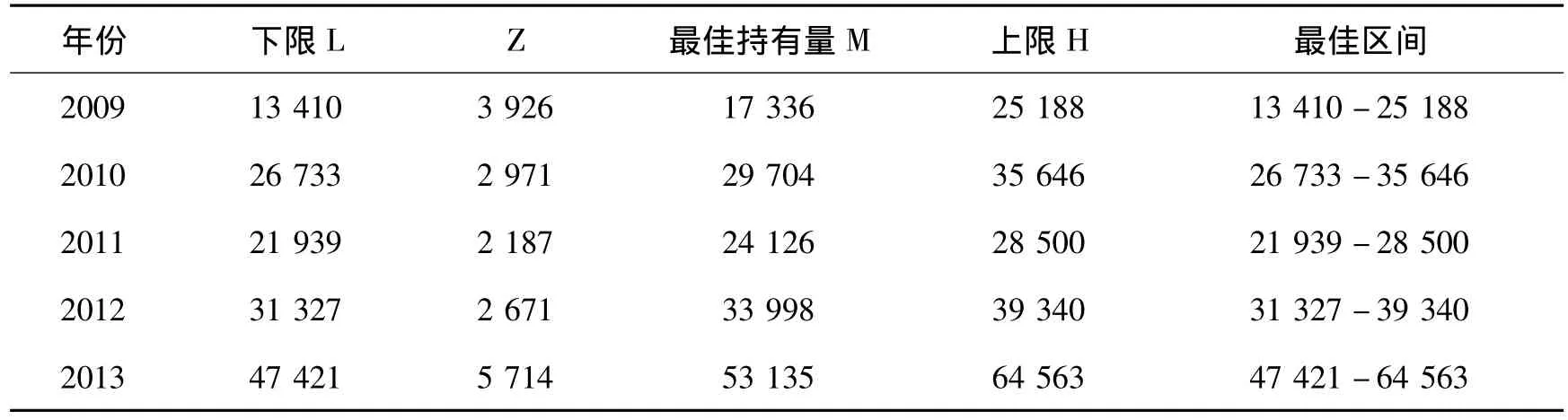
表4 2009—2013年X区国库现金最佳持有区间 单位:万元
综上所述,2009—2013年将X区国库现金持有量保持在最佳区间比较适合。当国库现金余额超过上限H时,可以将国库现金用于运作,直至国库现金降到最佳持有量M,当国库现金余额低于下限L,则认为政府行政的正常运转可能受到影响,应将运作的资金转换回国库。从各年份的最佳区间来看,约有70%的月份国库现金余额超过上限,这部分资金用于运作在保证安全的前提下可以带来一笔可观的收益。从2009—2013年的测算可以看到,最佳持有量和最佳区间总体趋势在逐渐上升,主要是因为随着财政收支的上涨,国库现金的流量也在相应上升,且国库集中支付改革和税收征管力度加大使得国库资金的流量也相应上涨。2013年的大幅上涨还有一部分原因是市区体制的改变造成。因此,在考虑2014年的最佳区间时,可通过上述方法预测计算出最佳持有量;还可将2013年的最佳持有区间加上一定比例的增幅,增幅比率可以考虑用2014年的财政收入增长比例来测算。最后综合考虑两种方法计算所得的最佳持有量来科学确定2014年的国库现金最佳持有量。
四、结语
通过对X区的实证分析我们可以看到,运用随机模型来计算国库现金最佳持有量是可行的,有利于提高预测的可操作性且管理起来更为灵活。但是,由于模型中的变量K、E都是变动的,因此计算出来的最佳区间也在不断变动。与此同时,由于国库集中支付制度在全国范围内还没全覆盖,随着经济的发展和国库集中支付改革的不断深入,下限L的取值也在不断调整上升当中,上文对2009—2013年国库现金最佳区间的计算也证明了这点。[4]此外,该模型没有考虑到其他因素的影响,例如国债、货币政策、各地网络现代化程度、管理水平等因素,还存在一定的局限性。因此,在使用该模型时,还需结合各种影响因素来综合确定国库现金最佳持有量,并对数据进行滚动调整,及时更新。我们应意识到,在实际的现金管理中,最佳持有量M只是一个博弈的结果,对于区间的管理应该重点放在可控区间上下限的调整上,这样才更符合实际。
[参考文献]
[1]周雪峰.关于地方国库现金最佳持有量的实证研究[J].内蒙古金融研究,2013 (8) : 14-19.
[2]黄虹,孙国荣.公司理财[M].合肥:安徽人民出版社,2011.
[3]袁庆海,杜婕.中国国库现金最佳持有水平估计及预测——基于改进的Miller-Orr模型[J].财贸研究,2012 (5) : 74-82.
[4]王俊霞,邓晓兰,赵榆森,等.基于Miller-Orr模型的省级政府现金管理实证研究[J].当代经济科学,2006 (9) : 103-108.
(责任编辑陈蒙腰)
A Study on Treasury Cash Management——Based on the Optimal Cash Holdings
GAN Lu
(The Treasury Payment Center of Siming District,Xiamen 361004,China)
Abstract:Estimating scientifically the optimal treasury cash holdings is the key to operate treasury cash management successfully.The paper combined a theoretical analysis with empirical research methods,compared four commonly used models for estimating the optimal cash holdings,and established a method based on the stochastic model.Finally,by taking as an example the financial operation of a district of Fujian,the optimal cash holdings of the district’s treasury were estimated by using the stochastic model.The study showed that using the stochastic model to estimate the optimal cash holdings of treasury was feasible.It could promote the maneuverability and flexibility of treasury cash management.
Key words:treasury cash; optimal cash holdings; stochastic model
[作者简介]甘璐(1980—),女,福建龙海人,会计师、经济师,硕士,主要从事财政税收研究。
[收稿日期]2014-06-25[修回日期]2014-09-17
[中图分类号]F 812.2
[文献标识码]A
[文章编号]1008-889X (2015) 01-51-06

