BTA钻杆系统的涡动偏心及压电控制研究

BTA钻杆系统的涡动偏心及压电控制研究*

苗鸿宾a,b，邱泉水a,b，江敏a,b

(中北大学 a.机械与动力工程学院；b.山西省深孔加工工程技术研究中心，太原030051)

摘要：对BTA钻杆系统偏心运动的控制方法进行了研究，分析了钻杆系统的偏心运动方式和受力情况。基于线性二次型(LQR)最优模态控制，提出了一种压电主动控制方法。利用压电BTA钻杆理论，结合MATLAB软件对涡动控制进行仿真。仿真结果验证了压电主动控制方法的合理性，对BTA钻杆系统的运动稳定性控制的研究具有理论意义。

关键词：BTA钻杆；涡动偏心；压电控制

文章编号：1001-2265(2015)09-0091-04

收稿日期：2014-11-28；修回日期：2014-12-25

基金项目：*国家自然科学

作者简介：苗鸿宾(1970—)，男，山西阳泉人，中北大学教授，博士，研究方向为深孔加工技术;

中图分类号：TH113；TG65

The Research of Eccentric Motion of Whirling and Piezoelectric Control of

BTA Deep-hole Drill Pipe System

MIAO Hong-bina,b，QIU Quan-shuia,b，JIANG Mina,b

(a.School of Mechanical and Power Engineering;b.Shanxi Province Deep Hole Machining Center，North University of China，Taiyuan 030051，China)

Abstract：The control method of eccentric motion of BTA deep-hole drill pipe system is studied，and the eccentric motion mode and stress distribution of the system are analysed．Based on the linear quadratic regulator (LQR) modal control，a kind of piezoelectric active control method is proposed．Using the theory of piezoelectric BTA drill pipe，and combined with MATLAB software to simulate the control of whirling．The simulation verifies the rationality of the method of piezoelectric active control，and it has theoretical significance for the BTA drill pipe system movement stability control research．

Key words： BTA drill pipe；eccentricity of whirling；piezoelectric control

0引言

深孔加工是指钻削长径比能达到五倍以上的一种加工工艺，其钻杆结构细长，刚度较差，容易出现振动偏心、弯曲变形等。深孔加工中的钻杆由于振动偏心及不平衡力作用的影响，使钻杆系统存在着公转和自转，因而形成涡动[1]。涡动是一种偏心运动，因此本文着重对钻杆的偏心运动及其控制方法进行了研究。

目前国内外对深孔钻杆稳定性的研究还比较少，更多的是在石油钻杆上的研究。在涡动方面，1986年，Fujii等[2]研究发现不同刃弧角度刀具对钻杆的涡动行为有影响，阐述了涡动发展规律和抑制钻杆振动的方法。Gessesse等[3]通过实验研究了在深孔加工中孔壁螺旋刮痕的形成原因。Zhou等[4]借助动态模型分析中的技术和方法来抑制旋转机械中的振动。孔令飞等[5]研究了钻杆系统的非线性动力学，基于转速、偏心等情况下，建立了钻杆的流体动压模型。在压电控制方面，Palazzolo等[6]在旋转机械中利用压电致动器控制主动振动，而控制传感器为两个涡流传感器。Lee等[7]最早给出了模态传感器与模态驱动器的设计方法，并用于控制梁的横向偏心振动，取得了较好的控制效果。

深孔钻杆系统的涡动及其控制研究正逐步引起广大学者的关注。正是由于涡动现象对钻杆稳定性和深孔加工的重要影响，笔者在前人的基础上，对钻杆系统的涡动行为进行了全面地分析和研究，同时利用压电主动控制方法来实现对钻杆涡动偏心的控制。研究结果对于BTA深孔加工的动态稳定性研究具有理论和实际意义。

1BTA钻杆系统的涡动偏心

图1　钻杆涡动在孔壁上产生的螺旋刮痕

偏心运动是钻杆的一种典型失稳现象，其对BTA加工系统的加工精度、加工效率以及刀具的耐用度等都有很大影响。其形成原因是偏心钻杆轴线做摆转运动。由图1所示的孔壁的横向和纵向截面可以看出，加工孔内壁有一圈圈的刮痕，并呈螺旋形分布，这是因为钻杆在偏心运动的同时还有进给运动。

图2　BTA钻杆整体受力模型

如图2所示，钻杆形心轨迹为(x，y)，则转动质心的运动轨迹为(x+excosωt+eysinωt，y+eycosωt-exsinωt)，其中ex和ey为钻杆质心在x和y方向上的偏心分量。图中Flx和Fly为切削液流体力在x和y方向上的分量，假设不随角度变化而改变。Fcx和Fcy为钻削力在x和y方向上的波动分量，由质心运动定理可求出钻杆的动力学方程：

(1)

式中，m为钻杆质量；ω为钻杆角速度；E、I为钻杆的弹性模量与转动惯性矩；l为钻杆长度。

深孔加工中，不计纵向运动，在钻杆接触到孔壁之前，其横向运动可以分解为三种形式：钻杆的径向摆动、钻杆绕孔眼中心的公转、钻杆绕自身轴线的自转。而在这三种形式并存时，钻杆的横向受力可能是不平衡的。当钻杆旋转钻削时，其受力较为复杂，不仅受到钻头部位传递过来的切削力和钻杆本身弯曲变形所产生的弹性力，还受到液固耦合产生的扰动力。其中钻杆的切削力不是引起钻杆涡动角频率变化的原因，因而不参与计算。综合起来，流体力是影响钻杆涡动的主要原因，其它微小影响因素忽略不计[8]，如图3所示。

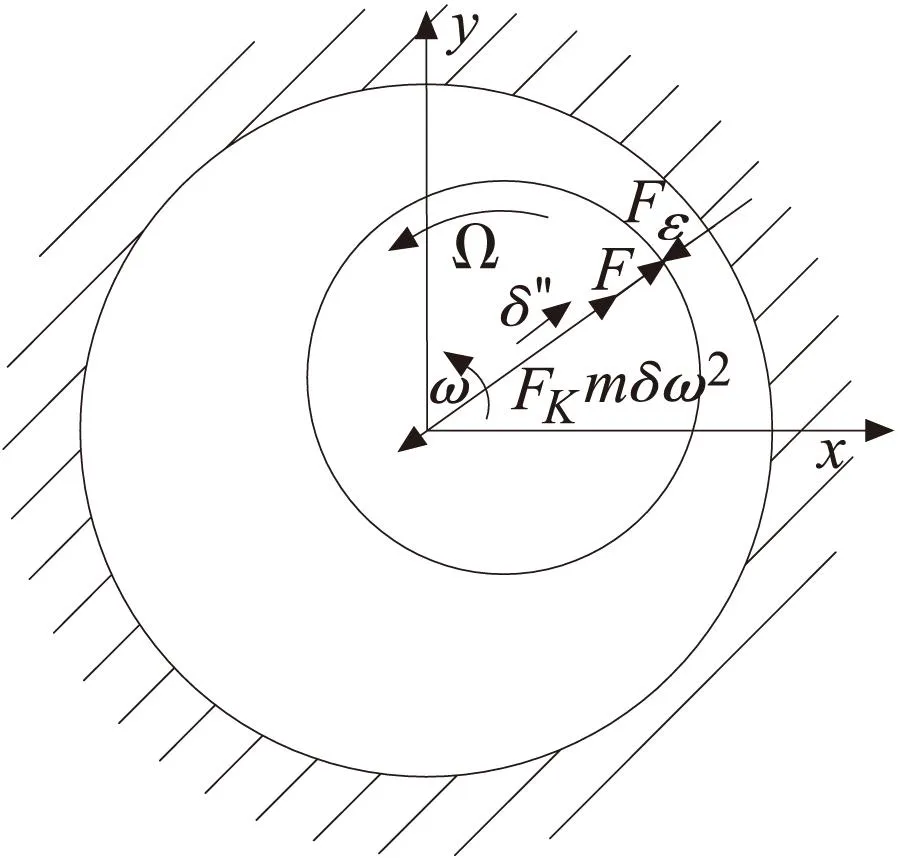
图3　钻杆动力学平衡示意图

若设涡动存在，则可建立钻杆动力学平衡方程：

mδ″=mδω2+F-Fε-Fk

(2)

式中，m为钻杆涡动段的质量；δ″为偏心方向上的加速度；δ为钻杆的偏心距离；ω为钻杆的涡动频率；F为内切削液对钻杆的流体扰动力；Fε为外切削液对钻杆的流体扰动力；Fk为钻杆变形产生的弹性力。

2BTA钻杆系统的压电控制

本文基于LQR最优模态控制来设计控制系统，建立机电耦合的压电BTA钻杆结构动力学方程，对BTA钻杆的偏心运动进行抑制。其方法是把压电陶瓷片粘贴在钻杆表面，即形成压电 BTA 钻杆结构，压电传感器接收振动偏移信号，控制处理器收到信号，信号放大器把信号放大传给执行元件，触发其对钻杆产生动作，使系统结构产生相应的应变，进而改变结构系统的动态阻尼，最终实现对偏心运动的控制。

2.1线性二次型最优控制法(LQR)

线性二次型最优控制法(LQR)[9]是按指定要求使系统达到预期的某一性能指标。如果控制系统是线性的，性能泛函是状态变量和控制变量的二次型函数的积分，则这样的最优控制问题称为二次型最优控制问题，简称线性二次型。线性二次型问题解出的控制规律是状态变量的线性函数，通过状态变量的反馈便可实现闭环最优控制。

假设系统的线性状态空间可表示为：

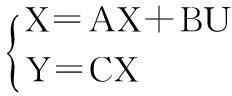
(3)

为研究各个向量之间的关系，引进系统的二次性能泛函——存留能量指标[10]：

(4)

式中，Q和R为控制输入矩阵，可取

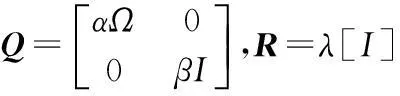
式中，α、β、λ为权系数。

若Q取值较大，则钻杆的振动衰减较快；当R=0时的二次型最优控制问题被称为“最短响应时间”问题；相反，若R取值较大，则可减少能耗。最优问题的求解就是寻找最优控制U，将系统从初始状态转移到零状态附近，并使二次性能泛函取最小值。其中：

(5)

式中，K为反馈增益矩阵；D为Riccati方程-DA-ATD+DBR-1BTD-Q=0的解[11]。

2.2BTA钻杆的压电控制

如图4所示钻杆外孔壁上均布四块压电片，压电传感结构和压电致动结构对贴于钻杆的直径上，两者相互对称。设钻杆的有效长度为L，外径和内径分别为D和d，x1、x2表示压电片两端到驱动端的距离，压电陶瓷片长度、有效宽度和厚度分别为Lb、b和tb。假定压电片和钻杆外壁粘贴良好，不会脱落，同时不考虑压电片对钻杆系统特性的影响。

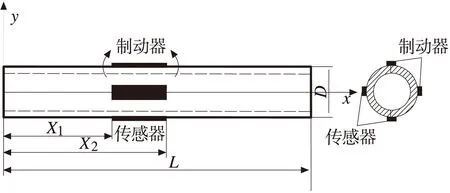
图4　BTA钻杆的压电控制模型

对于压电传感设备，可得其传感电压：

(6)

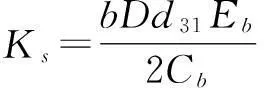
对于压电致动设备，致动器力为：

(7)

式中，Φi为固有振型；Ma为致动器力矩；Ua为控制系统输入致动器的电压；Ka为压电耦合系数；h(x)为赫维赛德阶跃函数。

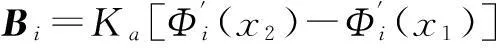
(8)

2.3BTA钻杆系统的压电控制结构

图5是在普通深孔机床上添加一套控制系统，其中贴附在钻杆上的是压电陶瓷片，在这里充当传感器和执行器，系统采用闭环反馈控制方法，其原理图如图6所示。

图5　BTA钻杆系统的压电控制结构图

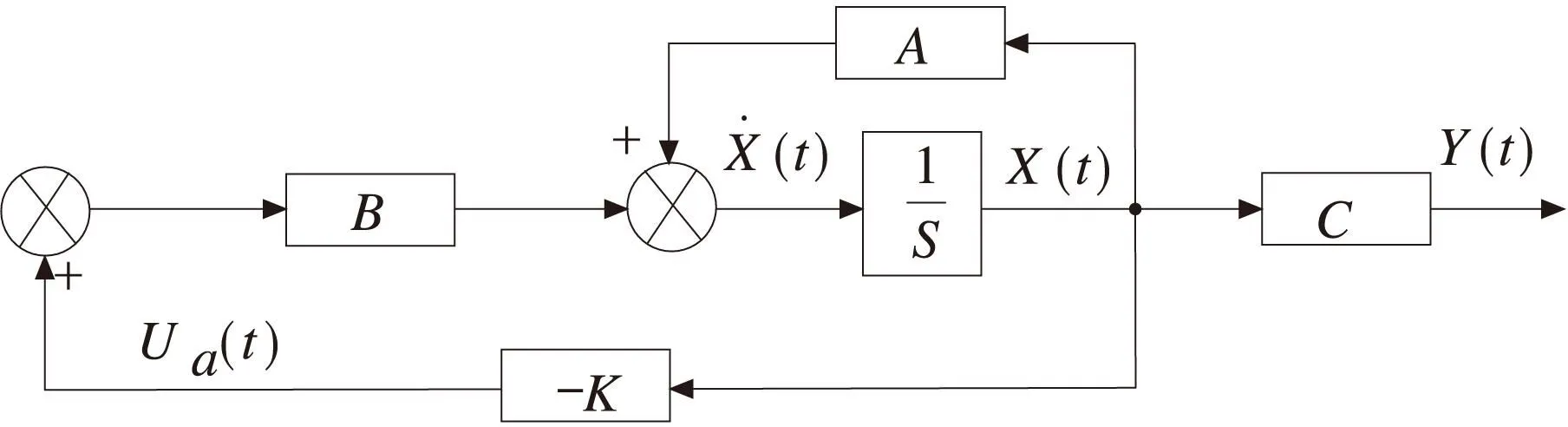
图6　系统反馈控制原理图

整个系统分为两个部分：振动结构体和智能控制系统。振动结构体主要是BTA钻杆系统的旋转振动，则主要控制对象是钻杆；而智能控制系统包括压电传感器、压电执行器、信号放大器、信号采集卡、控制平台及控制算法等。

2.4BTA钻杆系统的控制方程

(1)钻杆振动偏心方程

(9)

由固有振型展开定理，钻杆偏心位移可用其固有振型{Φi}线性组合来表示，即：

(10)

式中，Φ=[Φ1(x)Φ2(x)…Φn(x)]为质量归一化后的固有振型矩阵；q=[q1(t)q2(t)…qn(t)]T为模态坐标向量。

(2)钻杆状态方程

建立钻杆系统的状态空间动力学模型，引入状态空间向量，则有：

因此，式(8)和式(10)的状态空间方程为：

(11)

式中，Y(t)为钻杆系统的输出，表示为钻杆涡动横向位移；A、B和C分别为系统状态矩阵、系统控制矩阵和系统输出矩阵，具体如下：

Ka=bd31Eb(tb+D)为压电耦合系数，d31为压电常数，b为压电片宽度，Eb为钻杆弹性模量，tb为压电片厚度，D为钻杆外径。

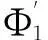
(12)

其固有振型及一阶导数为：

Φi(x)=sin(βix)+Dicos(βix)+

Eisinh(βix)+Ficosh(βix)

Eicosh(βix) +Fisinh(βix)

(13)

则有一阶振动模态：β1=1.875/L，D1=-0.091，E1=-1，F1=0.091。

3MATLAB控制仿真

结合钻杆正则模态方程，利用LQR控制法对压电钻杆一阶模态做仿真分析。

钻杆参数：材料为45号钢，弹性模量E=2.1×1011Pa，密度ρ=7.9×103kg/m3，长度L=2000mm，外径D=35mm，内径d=24mm。

压电陶瓷片参数：弹性模量ED=6.3×1010Pa，压电常数D31=-1.2×10-10C/N，厚度tb=5mm，有效宽度b=12mm，压电陶瓷的电容率EP=7.3×10-12，电容量CP=5.8×10-12。

另设系统阻尼比ζ=0.1，初始条件X(0)=(0.01，0)。利用MATLAB编程，得到压电控制下的钻头位移图和控制电压图如下：

对比图7~图9，可以看出，基于LQR模态控制的压电主动控制可以控制钻杆的振动偏心，使BTA钻杆系统最终趋于平稳状态；同时还发现，电压输出与钻杆振动偏心距离大小成正比，即表现在压电片的应变与位移成比例，而应变又与电量成正比。随着压电控制的持续，BTA钻杆振动偏心位移不断减小，因而压电传感器接收到的信号不断减弱，从而使系统输出的控制电压不断减小，以便保持钻杆系统的运动平稳。

对比图8和图9，可以看出，增大LQR控制法中的权矩阵Q，能加快钻杆振动偏心位移的衰减，这验证了前面的理论；从数据上来看，Q=[103，0；0，103]，R=0.001时，反馈增益系数K=[0.0456，15.4994]，性能指标J=16.9975；而Q=[106，0；0，106]，R=0.001时，反馈增益系数K=[46，12917]，性能指标J=14165.5485；显而当Q较大时，能加快振动衰减，但是比较耗能，而Q较小时能耗较小，这也是其控制电压小于前者的原因。

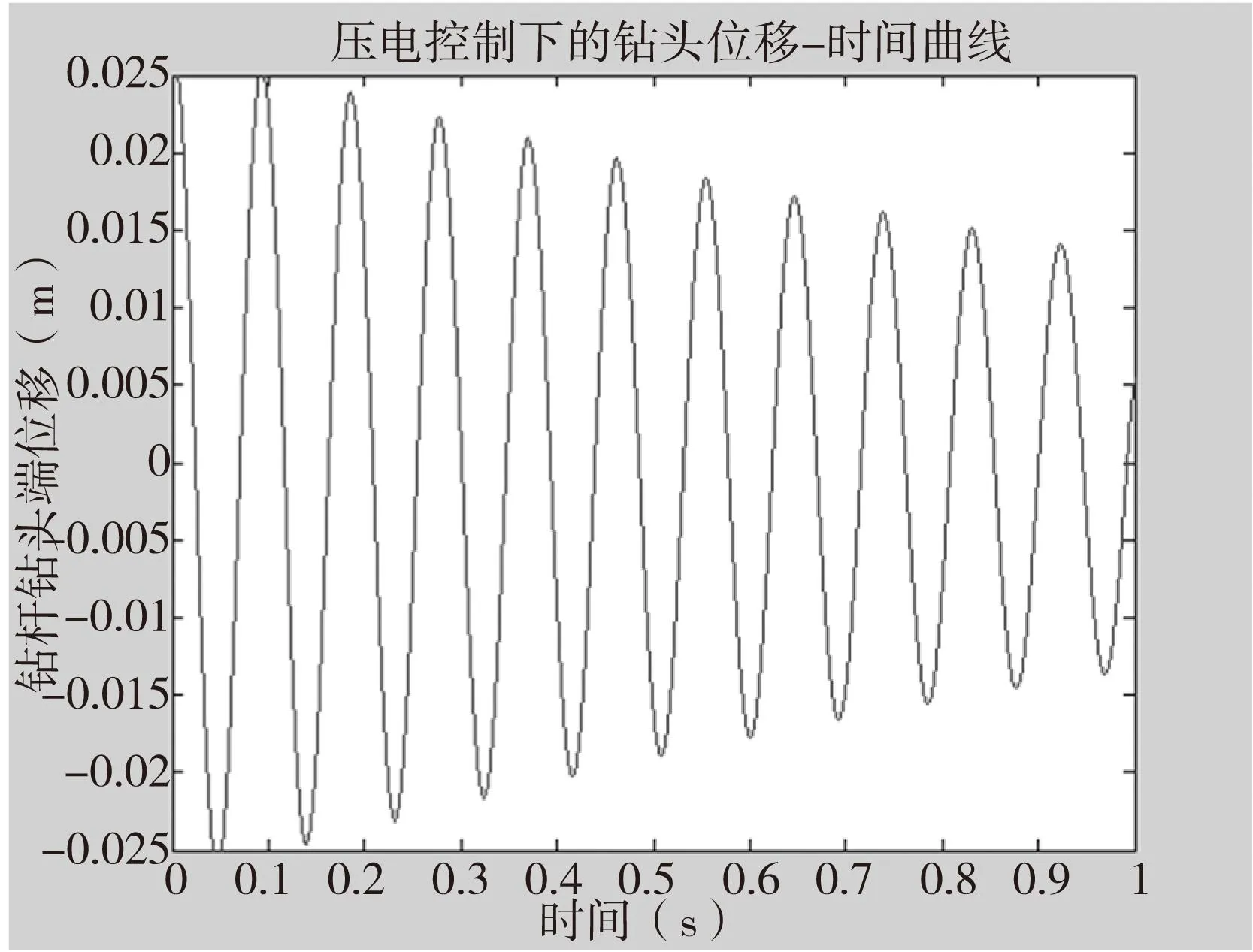
图7　未加控制下的自由阻尼偏心振动

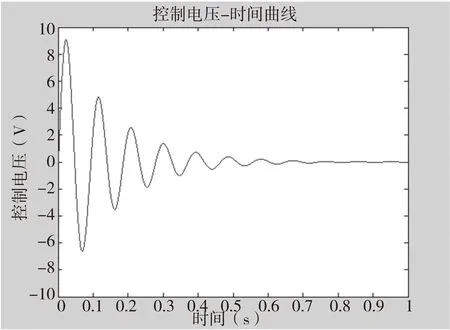
图8　钻杆在施加控制( Q=[10 3，0；0，10 3])仿真结果

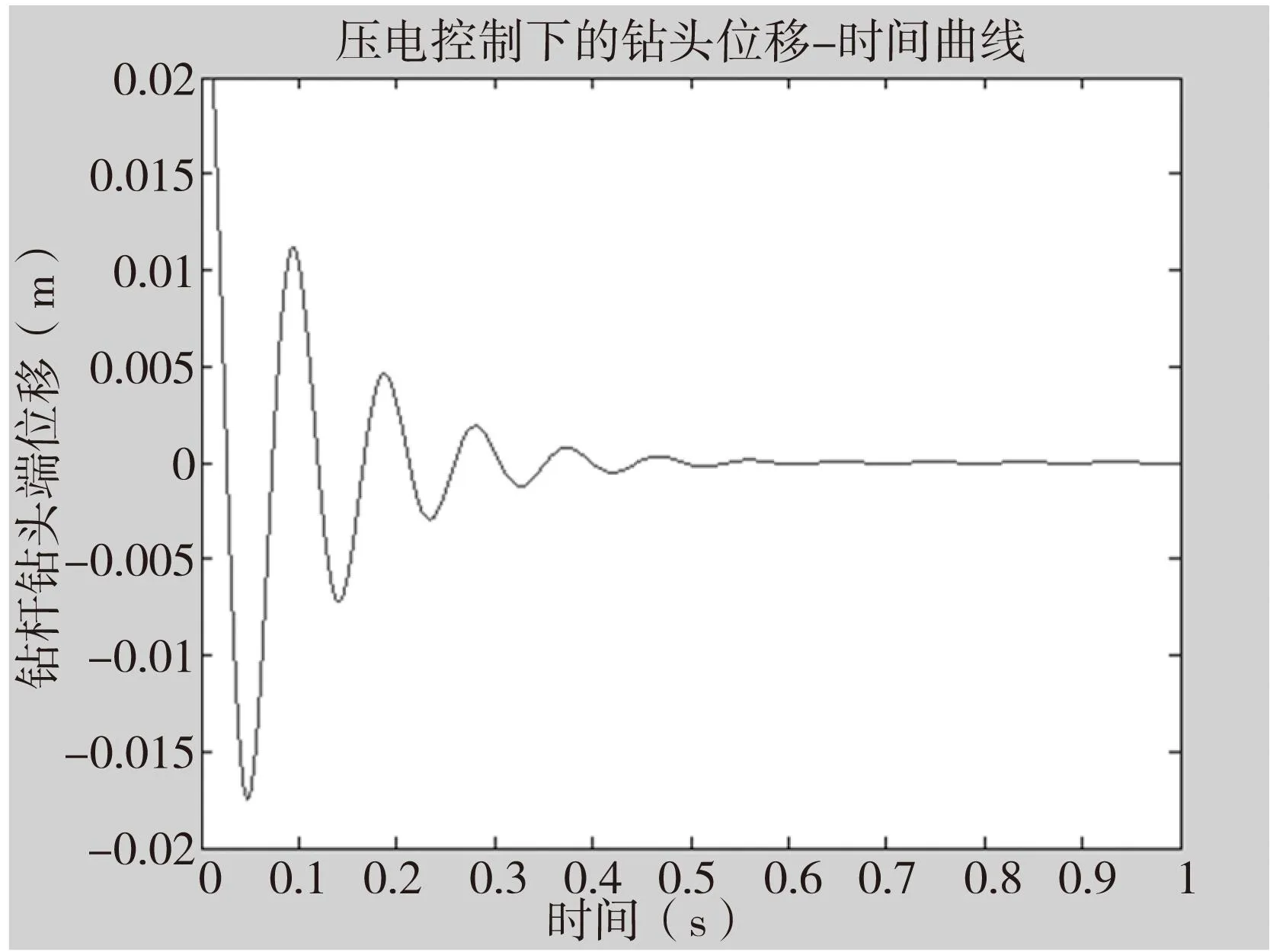
图9　钻杆在施加控制( Q=[10 6，0；0，10 6])仿真结果

4结束语

(1)本文分析了钻杆系统的偏心运动方式和受力情况，基于LQR最优模态控制法构建了压电BTA钻杆主动控制模型，并进行了理论推导。

(2)利用 MATLAB 进行编程求解并对其进行压电主动控制仿真，得到BTA钻杆的钻头位移图和控制电压图，仿真结果表明基于LQR最优模态控制的压电主动控制方法能够有效地抑制钻杆涡动偏心的发生。

[参考文献]

[1] 孔令飞，李言，吕延军,等．BTA深孔加工非线性流体力的分布特性[J]．机械科学与技术，2009，28(3)：340-345．

[2] H Fujii，E Marui，S Ema．Whirling Vibration in Drilling-part1：cause of vibration and role of chisel edge[J]．ASME Journal of Engineering for Industry，1986，108：157-162．

[3] Y Gessesse，B Lationovic，M Osman．On the Problem of Spiraling in BTA Deep-hole Machine[J]．Transactions of ASME，Journal of Engineering for Industry，1994，116：161-165．

[4] S Zhou，J Shi．Active Balancing and Vibration Control of Rotating Machinery：A Survey[J].The Shock and Vibration Digest，2001，33(4)：361-371．

[5] 孔令飞．深孔加工中钻杆系统非线性动态行为研究[D]．西安:西安理工大学，2010．

[6] A Palazzolo，R Lin，R Alexander，et al．Test and Theory for Piezoelectric Actuator-Active Vibration Control of Rotating Machinery[J]．Journal of Vibration and Acoustics，1991，113：167-175．

[7] Lee C K，Moon F C．Modal sensors and actuators[J]．Journal of Applied Mechanics，1990，57(2)：434-450．

[8] 江敏，苗鸿宾，高腾．内外切削液共同作用下的BTA钻杆的涡动条件[J]．机床与液压，2013，41(23)：20-23．

[9] 刘豹，唐万生．现代理论控制[M]．北京：机械工业出版社，2006．

[10] 黄国权，王铁桩．压电智能板动力学有限元模型建立及振动控制(Ⅱ)—压电智能板振动控制[J].组合机床与自动化加工技术，2006(9):57-59．

[11] 李晓慧，郭庆鼎．数控机床直线伺服系统混合LQ-H∞控制器设计[J].组合机床与自动化加工技术，2007(2):38-41．

(编辑李秀敏)