2015年高考数学必做客观题【2】
2015-12-29 00:00:00陶友根
数学教学通讯·初中版 2015年8期


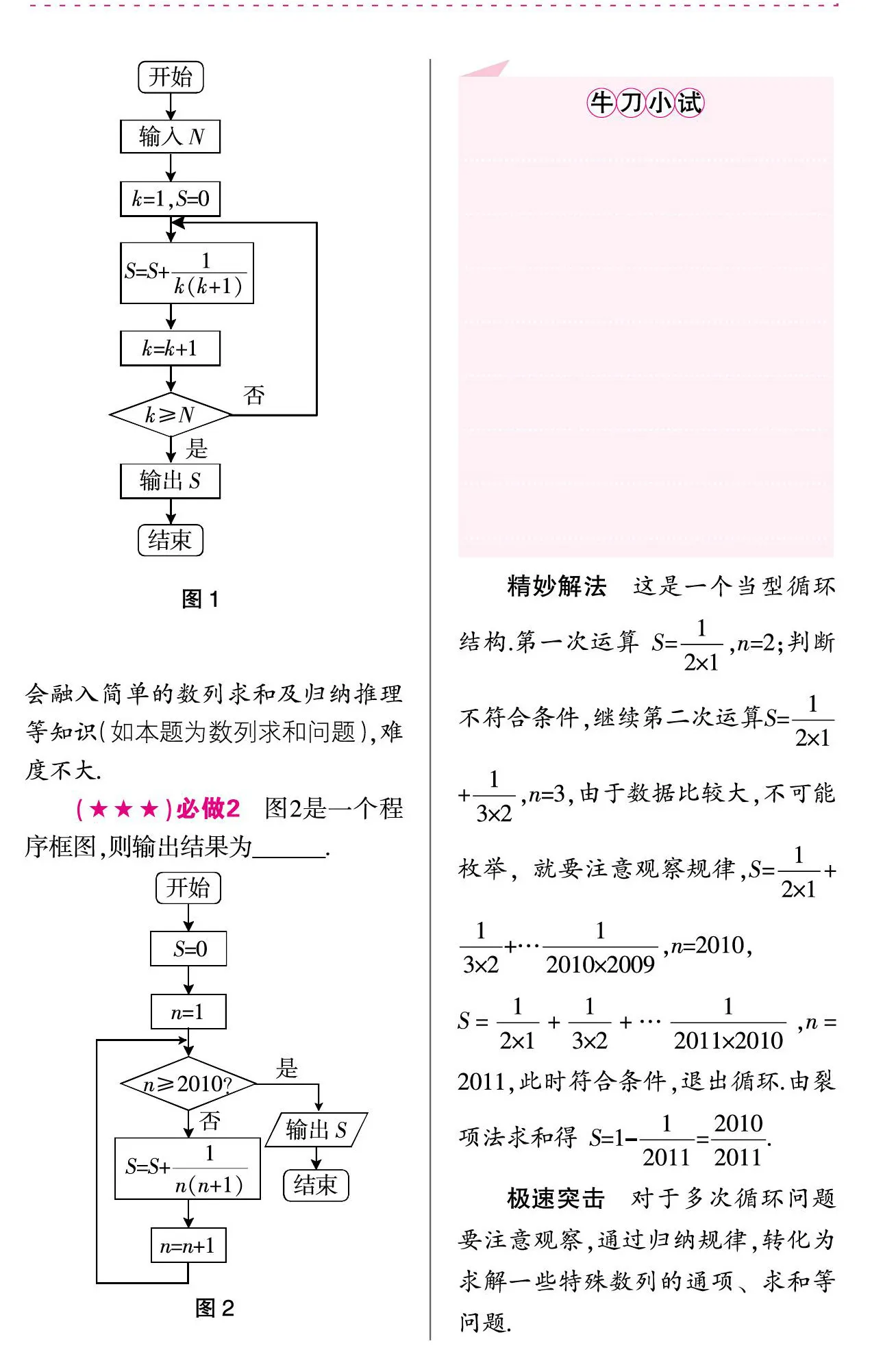


必做1 一个小朋友有5支不同颜色的水彩笔,老师要求用这5支笔给图中的四个区域涂色,规定一个区域只涂一种颜色,相邻的区域颜色不同,那么小朋友有______种不同的涂色方案.
图1
精妙解法 先分为两类:
第一类,当D与A不同色,则可分为四步完成.第一步,涂A有5种方法;第二步,涂D有4种方法;第三步,涂C有3种方法;第四步,涂B有3种方法. 由分步乘法计数原理,共有5×4×3×3=180种方法.
第二类,当D与A同色,分三步完成,第一步,涂A和D有5种方法;第二步,涂B有4种方法;第三步,涂C有4种方法. 由分步乘法计数原理,共有5×4×4=80(种).
所以共有180+80=260种不同的方案.
极速突击 首先确定“完成一件事”的“事”是什么,再判断是“分类”还是“分步”,从而确定用“加法”还是“乘法”进行计数. 染色问题是考查计数方法的一种常见问题,由于这类问题常常涉及分类与分步,所以在高考题中经常出现,处理这类问题的关键是要找准分类标准,像本题中A,D颜色是否相同对其他区域的涂色有影响.
误点警示 本题容易出现如下错解. 分四步完成:第一步,涂A有5种,第二步,涂B有4种,第三步,涂C有4种,第四步,涂D有3种,所以共有5×4×4×3=240种.错误的原因在于没有考虑到A,D是否同色对B,C区域的影响.

