复广义正定矩阵的定义及其相关性质

蔺小林, 蔺彦玲

(陕西科技大学 理学院， 陕西 西安　710021)



复广义正定矩阵的定义及其相关性质

蔺小林, 蔺彦玲

(陕西科技大学 理学院， 陕西 西安710021)

摘要：在实正定矩阵、广义实正定矩阵和复正定矩阵定义及其性质的基础之上，给出了复广义正定矩阵的定义及其一些性质，并对相关性质给出了详细完整的证明，推广了实正定矩阵、广义实正定矩阵和复正定矩阵的相关结论.

关键词：复广义正定矩阵; Hermite矩阵; 性质

0引言

在矩阵论的研究中，矩阵的正定性是其研究的重要分支之一，不管是在理论上还是实践应用中，正定矩阵都有着非常重要的作用.而在矩阵的正定性认识与探讨中，历史上最早对实对称正定矩阵进行了定义，如下：

定义1[1]n阶实对称矩阵A，如果对任意的X∈Rn×1(X≠0)，都有XTAX>0，则称A为正定矩阵.这类正定矩阵全体用集合PS来表示.

1970年，Johnson给出了未必对称的实矩阵的正定性定义.

定义2设A∈Rn×n，如果对于任意的X∈Rn×1(X≠0)，都有XTAX>0，则称A为正定矩阵.

这类正定矩阵的全体用集合PI来表示.

在以上实正定矩阵的定义下，许多学者对实正定矩阵的定义进行了推广.其中，1988年，夏长富对正定矩阵进行了深层次的定义：

定义3[3]设A∈Rn×n，如果对任意的X∈Rn×1(X≠0)，都存在正定对称矩阵S=SX∈PS,使得XTSXAX>0，则称A为广义的正定矩阵.如果S=SX与X无关，则把这类正定矩阵的全体用集合PS+表示.

在矩阵正定性的研究中，很多学者不仅研究了实正定矩阵的正定性问题，还研究了复正定矩阵的正定性问题，最开始对复矩阵正定性的定义仅仅局限于Hermite矩阵，如下：

1985年，Horn和Johnson对未必对称的复矩阵给出了正定性的定义.

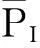
除了以上作者对不同正定矩阵进行定义及其性质进行研究外，后来也有众多学者对正定矩阵进行了更深层次的探讨和推广，2005年YangShichun和WuWenquan[6]给出了广义正定矩阵的定义并研究了其相关性质.2010年，王志伟和王伟贤[7]探讨了正定矩阵的子式阵的正定型，2013年，黄毅[8]给出了复正定矩阵的一些性质并对复正定矩阵进行了分类，2014年，秦应兵[9]对广义正定矩阵进行了进一步的推广，同时，黄毅和欧鹏[10]也研究了亚正定矩阵的基本性质.

在实正定矩阵、广义实正定矩阵和复正定矩阵定义的启发下，受以上各种定义的影响，本文进一步推广了复正定矩阵正定性的定义，并且在该定义之下，对复广义正定矩阵的一些性质进行了深入探讨，得到了相关结论.

1主要结论

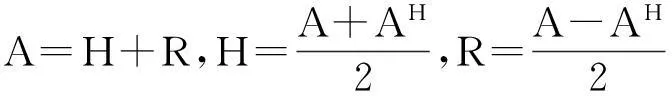
显然，

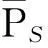
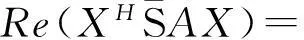
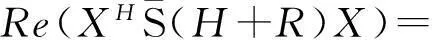
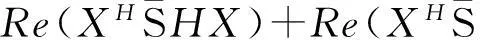
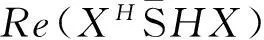
(1)

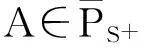
引理2[11]设A,B是复正定矩阵，则A+B是复正定矩阵；若k为正实数，则kA是正定复矩阵.

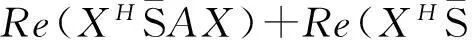
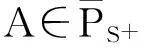
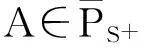
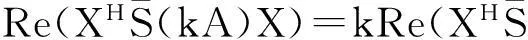
引理3[3]设A∈Rn×n，则A∈PS+的必要充分条件是，存在S∈PS，使SA+ATS∈PS.

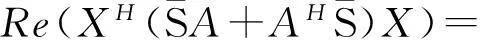
(2)

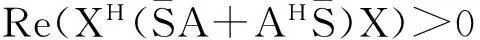
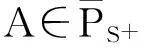
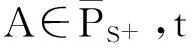
中，由于Re(t)>0，所以矩阵tE为实部均为正的对角矩阵，且其对角元素的实部为

Re(diag(tE))=diag(Re(t),Re(t),…,Re(t))，

该定理的证明类似于文献[11]中系5的证明，此处从略.

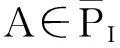
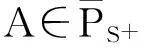
2结论

本文基于实正定矩阵和广义实正定矩阵的定义、性质以及相互关系，并根据复正定矩阵的定义和性质，给出了复广义正定矩阵的定义，讨论了复广义正定矩阵的相关性质并给出了证明，本文所给出的这些定义和所得到的相关结论推广了已有的有关正定矩阵的定义和某些结论，这些理论在矩阵论的研究和应用中具有一定意义.

参考文献

[1]王蕚芳，石生明.高等代数[M].3版.北京：高等教育出版社，2003:231-237.

[2]JohnsonCR.Positivedefinitematrices[J].AmerMonthly,1970,77:295-264.

[3]夏长富.矩阵正定的进一步推广[J].数学研究与评论，1988,8(4):499-504.

[4]张贤达.矩阵分析与应用[M].北京：清华大学出版社，2004:53-54.

[5]HornRA,JohnsonCR.MatrixAnalysis[M].England:CambridgeUniversityPress,1985.

[6]YangShichun,WuWenquan.Onthegeneralizedpositivedefinitematrices[J].MathematicsinPracticeandTheory,2005(5):146-150.

[7]王志伟，王伟贤. 关于正定矩阵的子式阵的正定性[J].数学的实践与认识，2010，40(11)：174-178.

[8]黄毅.复正定矩阵的性质和分类[J].成都大学学报，2013,32(3)：238-241.

[9]秦应兵.广义正定矩阵的等价定义及进一步推广[J].大学数学，2014,30(5):62-64.

[10]黄毅，欧鹏.亚正定矩阵的基本性质[J].成都大学学报(自然科学版)，2014,33(1)：20-22.

[11]李俊杰.论复矩阵的正定性[J].数学的实践与认识，1995,25(2):59-63.

[12]陈景良.特殊矩阵[M].北京：清华大学出版社，2001.

[13]张璐璐.关于广义复正定矩阵的若干结论[J].长春工程学院学报，2013,14(2):118-120.

Thedefinitionandpropertiesofacomplexgeneralizedpositivematrix

LINXiao-lin,LINYan-ling

(CollegeofScience，ShaanxiUniversityofScience&Technology,Xi′an710021,China)

Abstract:Based on the definitions and properties of a real positive matrix, a real generalized positive matrix and a complex positive matrix, the paper gave the definition and some properties of a complex generalized positive matrix, and various properties were detailed and complete proof.

Key words:a complex generalized positive matrix; Hermite matrix; properties

中图分类号：O151.21

文献标志码：A

文章编号：1000-5811(2015)05-0183-03

作者简介:蔺小林(1961-)，男，陕西洛川人，教授，博士，研究方向：数值计算理论及其应用

基金项目：陕西省科技厅重点实验室科技计划项目(2011HBSZS014)； 陕西科技大学学术团队计划项目(2013XSD39)

收稿日期:*2015-05-25