非线性φ-Laplace系统的半正问题
白定勇,盛其杰
(广州大学数学与信息科学学院,广东广州 510006)
0 Introduction
Throughout this paper,we assume that φ,φ1,φ2are all odd and increasing homeomorphisms from R onto R.Consider the positive solutions of the following nonlinear φ-Laplacian system
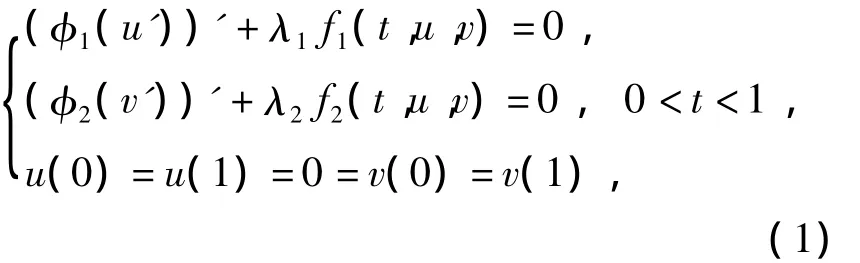
where λi(i=1,2)is positive parameter.
The function φ(u')satisfies two important cases φ(u')=u'and φ(u')=|u'|p-2u'(p>1).For the case φ(u')=|u'|p-2u'(p>1),φ-Laplacian problem reduces to one-dimensionalp-Laplacian problem.Therefore,system(1)is also known as generalizedp-Laplacian problem.Recently,the positive solutions of φ-Laplacian problems have attracted widespread attention.In Ref.[1],WANG studied then-dimensional system
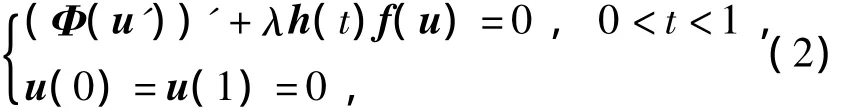
where u=(u1,…,un),Φ(u')=(φ(u'1),…,φ(u'n)),h(t)=diag[h1(t),…,hn(t)],and f(u)=(f1(u1,…,un),…,fn(u1,…,un)).With the help of fixed point theorems in a cone,results on the nonexistence and on the existence of one or two positive solutions for λ belonging to some open intervals are established.Then HENDERSON et al[2]also proved the existence of at least one positive solution of System(2)when Φ(u)=(q(t)φ(p(t)u1),…,q(t)φ(p(t)un)).Furthermore,the first author of this paper and CHEN[3]considered(2)withn=1 by using Leggett-Williams fixed point theorem and obtained the explicit open interval of parameter λ such that System(2)has at least three positive solutions.For more results on positive solutions of φ-Laplacian boundary value problems,see,for example,Ref.[4 -8]and the references therein.The above mentioned papers all need the positivity of the nonlinear terms.For the semipositone case,the existence of positive solutions of φ-Laplacian problems was studied only by HAI et al.[9],in which the following single form was considered:
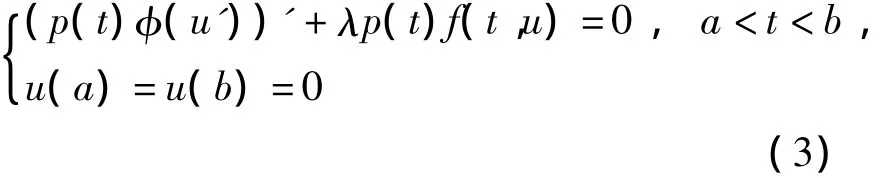
By a fixed point theorem in cones,the existence of at least one positive solution of System(3)was proved for λ > 0 sufficiently small underfsatisfying φ-superlnear condition(i.e.,
Motivated by the above works,we consider the semipositone problem of System(1)by fixed point method.Our main interest is the explicit open regions of(λ1,λ2)such that the System(1)has at least one positive solution.
Semipositone problems arise in many different areas of applied mathematics and physics,see e.g.Ref.[10-12],and were formally introduced by CASTRO et al in Ref.[13].The method of studying semipositive problems,in addition to fixed point method,more is the bifurcation theory,shooting method and time mapping analysis method.The research about this aspect[13-17]and the references therein.For the case of φi(u)=u(i=1,2),the first author of this paper considered the existence of positive solutions of System(1)[18],moreover,with XU[19]considered the system with delays by fixed point method.Therefore,this paper is a continuation of the researches in Ref.[18-19]and generalizes the corresponding results for a single form in Ref.[9].Our result is new even forp-Laplacian boundary value problems.
Now we state our main result.Assume that
(A1)φi-1(i=1,2)is concave on R+;
(A2)For eachc>0,there exists,such that φi-1(cu)≥),u∈R+andi=1,2;
(A3)fi:[0,1]×R+×R+→R is continuous,and there existsMi>0 such thatfi(t,u,v)≥-Mi,(t,u,v)∈[0,1]× R+× R+,i=1,2;
(A4)There existr1>0,r2>0 such that
(i)f1(t,u,v)≥0,(t,u,v)∈[0,1]×[0,r1]×R+;
(ii)f(t,u,v)≥0,(t,u,v)∈[0,1]× R+×
2[0,r2];
(A5a)=∞,uniformly fort∈[0,1]and the first limit being uniform forv≥0 and the second foru≥0;
(A5b)=∞,uniformly fort∈[0,1]and the first limit being uniform foru≥0 and the second forv≥0.
Theorem 1 Let(A1)~(A4)and either(A5a)or(A5b)hold.Then for each 0<r<min{r1,r2}System(1)has at least one positive solution for

whereχi(r)=sup0≤t≤1,0≤x,y≤rfi(t,x,y)+Mi(i=1,2).
In the discussion of semipositone systems by fixed point method,condition(A4)is used to guarantee the positive solution of auxiliary system is greater than the one of linear problem concerned.This condition was initiated by BAI[18]and BAI,et al[19].It was used also in Ref.[20]to discuss the positive solutions of a semipositone system.In these three pa-pers,r1andr2are taken specifically asr1=r2=1.
We say that(u(t),v(t))is a positive solution of System(1)if(u,v)∈C1[0,1]×C1[0,1],(φ(u'),φ(v'))∈C1[0,1]×C1[0,1]withu(t)>0,v(t)> 0 fort∈[0,1]and(u,v)satisfies(1).
The remaining part of this paper is organized as follows.In Section 1,we provide some preliminary results and cite the fixed point theorem used in the proof Theorem 1.Then,in Section 2,we show the proof of Theorem 1.Finally,we give an example to illustrate our main result.
1 Some preliminaries and lemmas
We introduce some preliminary results for the later use.
Lemma 1 Leth∈C[a,b]andh(t)>0,t∈[a,b].Assumeu,vsatisfy
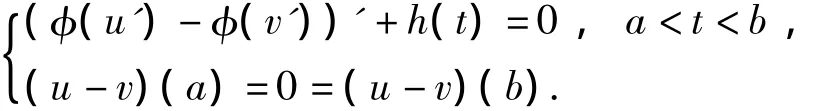
Thenu(t)>v(t),t∈(a,b).
Proof By way of contradiction,we assume that there existst0∈(a,b),such that(u-v)(t0)=(u-v)(t)≤0.By integrating fromttot0,we have φ(u'(t))-φ(v'(t))>0,t∈(a,t0),which implies(u-v)'(t)>0,t∈(a,t0)by the monotony of φ and hence(u-v)(t0)>0 by the boundary condition(u-v)(a)=0,which is a contradiction.
Lemma 2[9]Fori=1,2,letwsolves the
ifollowing problem
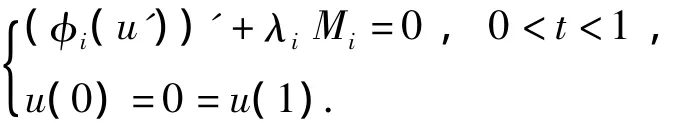
Thenwi(t)>0,and|w'i(t)|≤φ-1i(λiMi),t∈(0,1).
Lemma 3[9](i)Foru≥-κ,v≥0,κ≥0,

The following fixed point theorem is crucial in our proof.
Lemma 4[21]Let(E,‖·‖)be aBanachspace and letKbe a cone inEsuch that‖·‖ is monotone with respect to the coneK.LetT:K→Kbe a completely continuous operator.Assume there exist positive constantsr,Randk∈K,h∈Kwith 0 <r<R,‖k‖ <r,‖h‖ >R,such that
(i)For each θ∈(0,1),all solutionsu∈Kofu=θTu+(1-θ)ksatisfy ‖u‖≠r,
(ii)For each θ∈(0,1),all solutionsu∈Kofu=Tu+θhsatisfy‖u‖≠R.
ThenThas at least one fixed pointu∈Kwithr≤‖u‖ ≤R.
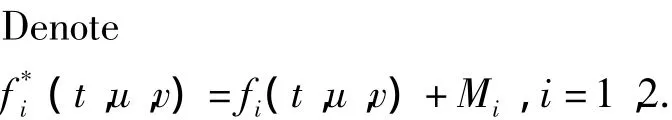
Lemma 5 (u,v)is a positive solution of system(1)if and only if(x,y)=(u+w1,v+w2)is a positive solution of the following system

andx(t) >w1(t),y(t) >w2(t),t∈(0,1).Here,

Obviously,problem(4)is equivalent to
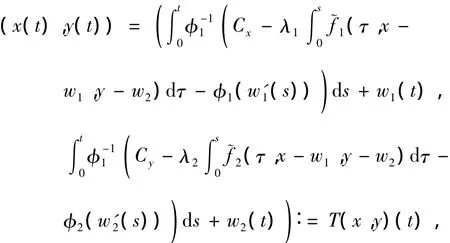
whereCxandCyis such thatx(1)=0 andy(1)=0,respectively.It can be verified that


Now,letX=C[0,1] with norm ‖x‖ =|x(t)|.LetE=X×X,then(E,‖(·,·)‖)is aBanachspace with norm ‖(x,y)‖ =max{‖x‖,‖y‖},(x,y)∈E.LetP={x∈X:x(t)≥0,t∈[0,1]},a cone inX,thenK=P×Pis a cone inE.For(u,v),(x,y)∈K,(u,v)≤(x,y)meansu≤xandv≤y.Then the norm‖(·,·)‖ onEis monotone with respect toK.It can be verified thatT:K→Eis completely continuous andT(K)⊂K.
2 Proof of Theorem 1

Here,we only consider the case that(A1)~(A4)and(A5a)hold.The case that(A1)~(A4)and(A5b)hold can be dealt with in a same manner.Define
We divide the proof into two steps.
Step I We shall apply Lemma 4 to show thatThas a fixed point(x,y)∈K,i.e.,the System(4)has a positive solution.
First,we show that for each θ∈(0,1)all solutions(x,y)∈Kof(x,y)= θT(x,y)satisfy ‖(x,y)‖≠r.Indeed,if there exists θ0∈(0,1)such that a solution(x,y)of(x,y)= θ0T(x,y)satisfies‖(x,y)‖ =r,then we have by(5)and Lemma 3(i)that fort∈[0,1],

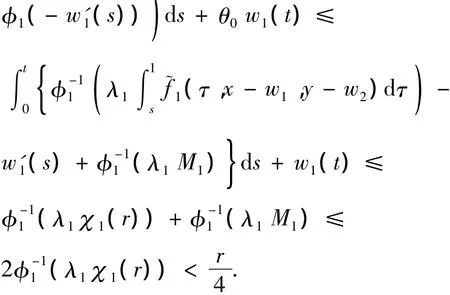
Similarly,y(t),t∈[0,1].Thus,we haver=‖(x,y)‖,a contradiction.
Next,we verify that there exist constantsR>randh1,h2>R,such that all solutions(x,y)∈Kof(x,y)=T(x,y)+ θ(h1,h2)(θ∈(0,1))satisfy‖(x,y)‖≠R.Such(x,y)satisfies

Without loss of generality,we suppose‖(x,y)‖ =‖x‖ =x(t0)>r.In the following we distinguish two cases(i)and(ii)to show it.Case(i).Letsolve

Then

By Lemma 1,x(t)>(t),t∈(0,t0).Note that

whereCis such that(0)=θh1.Hence
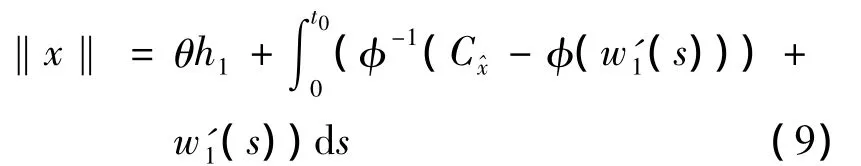
We claim that
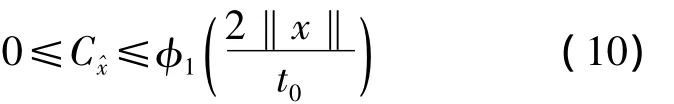

It follows by Lemma 3(i)that
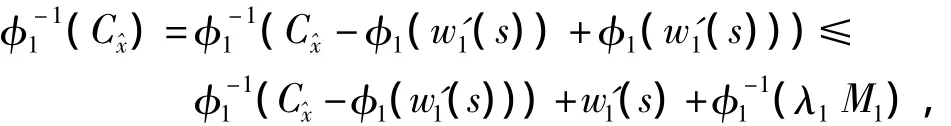
which implies
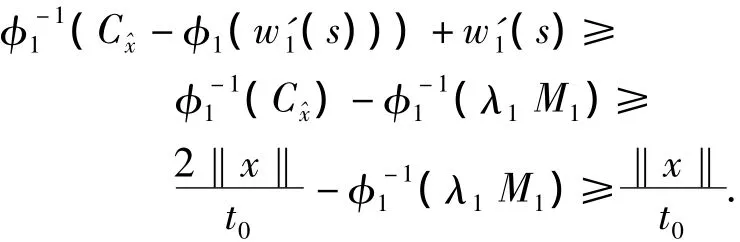
Thus,by System(9),we have‖x‖>θh1+‖x‖,a contradiction.Now,takeBy Lemma 3(i),(7)and(10),fort∈[t1,t0],we have


which yields that
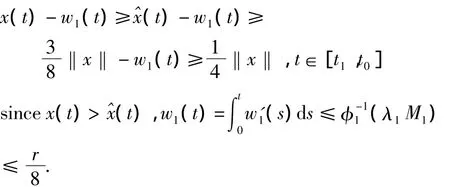
By the first equality of System(8),we have
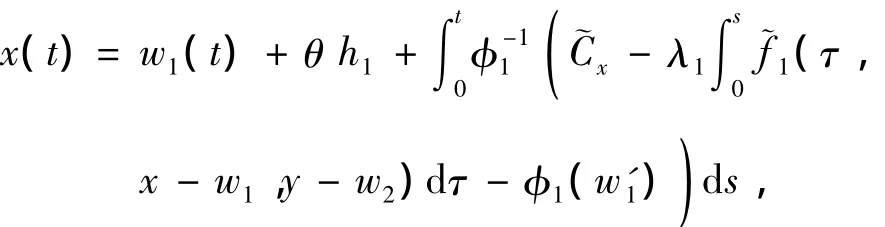

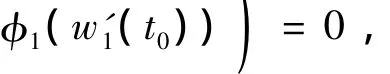
which implies τ.Then,fort∈[0,t0],

Therefore,

By(A5a),for‖x‖ large enough,we have

Thus,by assumption(A2),

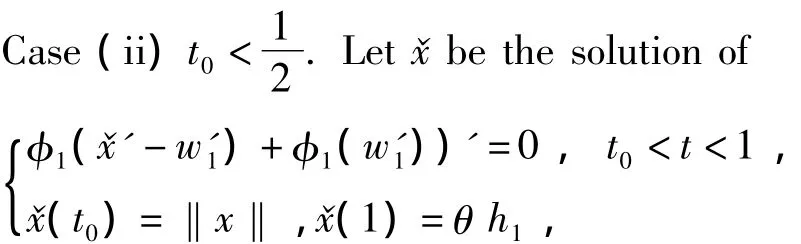
then

whereCis such that(1)=θh1.Thus
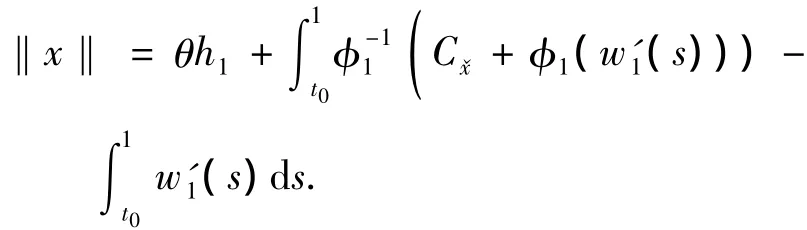
We claim that 0≤C≤φ1).In fact,if>,then

By Lemma 2,we have
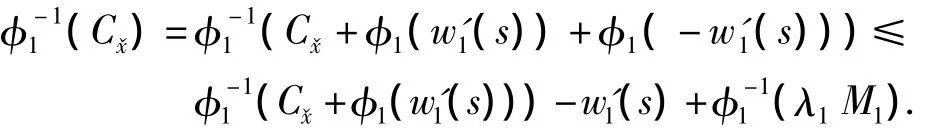
It follows
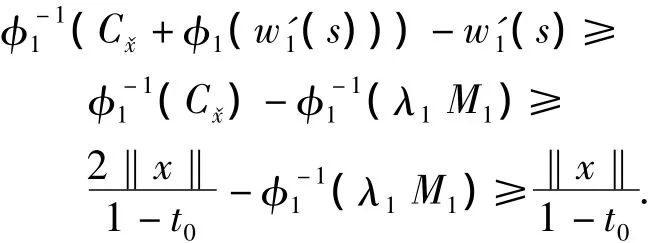
Therefore,‖x‖>θh1+‖x‖,contradiction.Now,taket2Then fort∈[t0,t2],we have
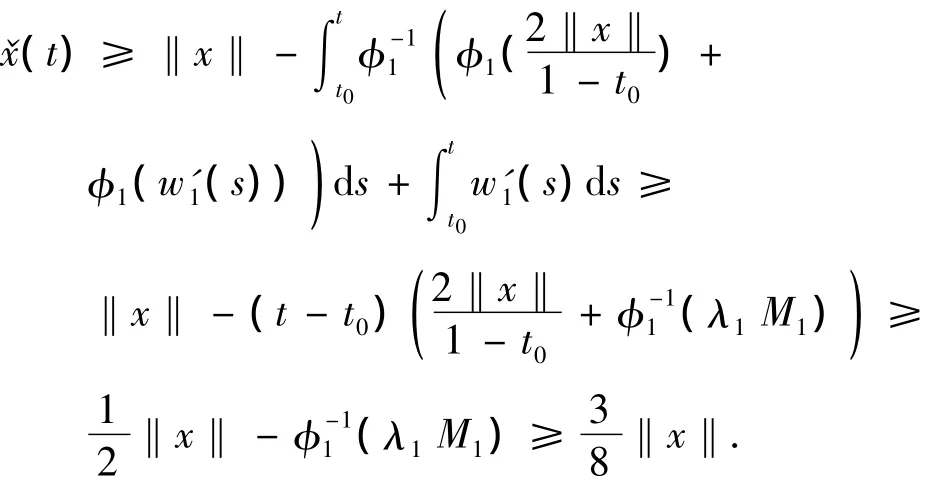
Note that
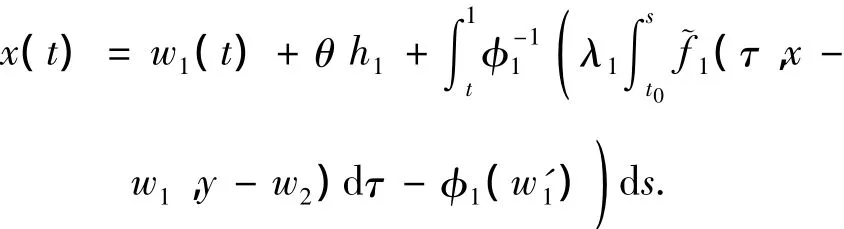
Similar to the discussion in Case(i),we know that there existsR2>r,independent of θ andh=(h1,h2),such that‖x‖ <R2.
In summary,in each case,there existsR>r,independent of θ andh=(h1,h2),such that all solutions(x,y)∈Kof(x,y)=T(x,y)+ θ(h1,h2)(0<θ <1)satisfy‖(x,y)‖ <R.Therefore,by Lemma 4,Thas a fixed point(x,y)∈K,which implies that System(4)has at least one positive solution(x,y)withr≤‖(x,y)‖≤R.
Step II We shall show thatx(t)>w1,y(t)>w2,t∈(0,1).
Letr≤‖(x,y)‖ =‖x‖ =x(t0)≤R,where 0 <t0<1.First,we show thatx(t)>w1,t∈(0,1).From the first equality of System(4)we obtain that for 0<t<t0,

Then,by Lemma 3(i),we have

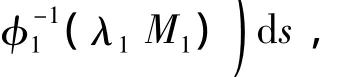
which implies

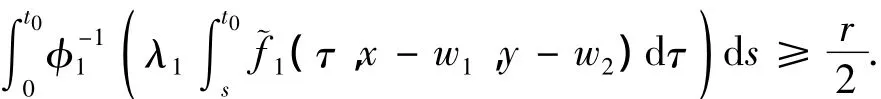
Therefore,by Lemma 3(ii),we have
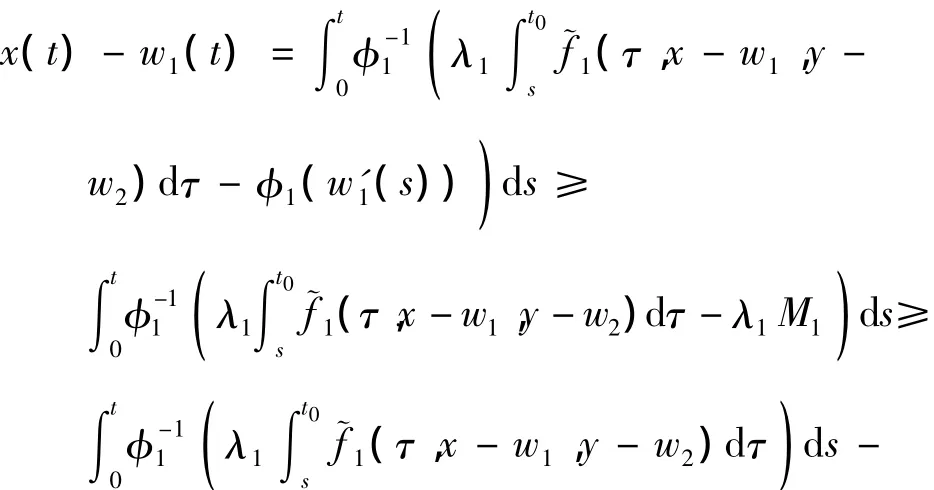
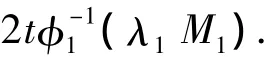
Note that the functionQw1,y-w2)dτ )dsis concave on [0,t0].Therefore

Similarlay,one can checkx(t)>w1(t)ont∈(t0,1).
Next,we distinguish two cases:(1)‖y‖≥rand(2)‖y‖ <rto provey(t)>w2(t),t∈(0,1).
Case(1)If‖y‖≥r,it can be checked by similar arguments as before.
Case(2)If‖y‖<r,let‖y‖ =y(t0),0<t0< 1 .Since(x,y)is a solution of(4),we have
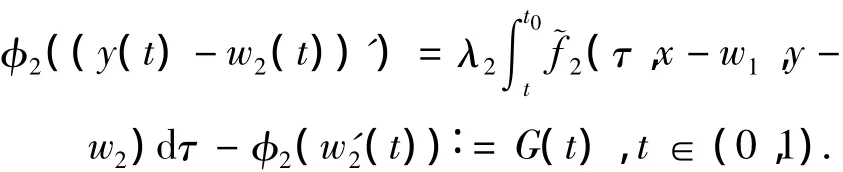
By the definition off2and assumption(A4)(ii),we have

Thus
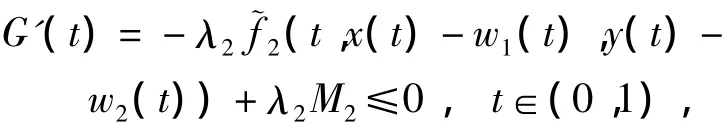
which implies thaty(t)-w2(t)is concave on[0,1].Therefore,y(t)≥w2(t),t∈[0,1].
Ifr≤‖(x,y)‖ = ‖y‖≤R,one can check similarly thatx(t)>w1(t),y(t)>w2(t),t∈(0,1).Therefore,by Lemma 5,(u,v)=(x-w1,y-w2)is a positive solution of the System(1).This completes the proof.
3 Examples
Letai>0,bi>0 andai<bi(i=1,2).Consider the following boundary value problem

Here, φ1(x)=,f1(u,v)=(u-
a1)(u-b1)+v2andf2(u,v)=(v-a2)(v-b2)+u2.It is easy to check that(A1)~(A4)and(A5a)hold.For eachc>0,we have.Obviously,Mi=For any given 0<r<min{a1,a2},χi(r)=aibi+r2(i=1,2).Therefore,Theorem 1 implies that System(11)has at least one positive solution for(λ1,λ2)

[1] WANG H.On the number of positive solutions of nonlinear systems[J].J Math Anal Appl,2003,281:287-306.
[2] HENDERSO J,WANG H.Nonlinear eigenvalue problems for quasilinear systems[J].Comput Math Appl,2005,49:1941-1949.
[3] BAI D,CHEN Y.Three positive solutions for a generalized Laplacian boundary value problem with a parameter[J].Appl Math Comput,2013,219:4782-4788.
[4] HENDERSON J,WANG H.An eigenvalue problem for quasilinear systems[J].Rocky Mount J Math,2007,37(1):215-228.
[5] BAI D,XU Y.Positive solutions and eigenvalue regions of two-delay singular systems with a twin parameter[J].Nonlin A-nal,2007,66:2547-2564.
[6] ARRÁZOLA E,UBILLA P.Positive solutions for the 1-dimensional generalizedp-Laplacian involving a real parameter[J].Proyecciones,1998,17:189-200.
[7] LEE E K,LEE Y H.A multiplicity result for generalized Laplacian systems with multiparameters[J].Nonlin Anal,2009,71:e366-e376.
[8] LIAN W C,WONG F H.Existence of positive solutions for higher-order generalizedp-Laplacian BVPs[J].Appl Math Lett,2000,13:35-43.
[9] HAI D D,SCHMITT K,SHIVAJI R.Positive solutions of quasilinear boundary value problems[J].J Math Anal Appl,1998,217:672-686.
[10] GIRO P,TEHRANI H.Positive solutions to logistic type equations with harvesting[J].J Differ Equ,2009,247(2):574-595.
[11] ORUGANTI S,SHI J,SHIVAJI R.Diffusive logistic equation with constant effort harvesting,I:Steady states[J].Trans Amer Math Soc,2002,354(9):3601-3619.
[12] ORUGANTI S,SHI J,SHIVAJI R.Logistic equation with thep-Laplacian and constant yield harvesting[J].Abstr Appl A-nal,2004,2004(9):723-727.
[13] CASTRO A,SHIVAJI R.Nonnegative solutions for a class of nonpositone problems[J].Proc Roy Soc Edinburgh,1988,108(3/4):291-302.
[14] GADAM S,IAIA J A.Exact multiplicity of positive solutions in semipositone problems with concave-convex type nonlinearities[J].Elect J Qual Theory Differ Equ,2001,4:1-9.
[15] LI H,SUN J.Positive solutions of superlinear semipositone nonlinear boundary value problems[J].Comput Math Appl,2011,61:2806-2815.
[16] DRAME A K,COSTA D G.On positive solutions of one-dimensional semipositone equations with nonlinear boundary conditions[J].Appl Math Lett,2012,25:2411-2416.
[17] HUNG K C.Exact multiplicity of positive solutions of a semipositone problem with concave-convex nonlinearity[J].J Differ Equ,2013,255:3811-3831.
[18] BAI D.Existence of positive solutions of nonlinear second-order differential systems[J].Acta Math Sci,2003,23(1):38-44.
[19] BAI D,XU Y.Positive solutions of second-order two-delay differential systems with twin-parameter[J].Nonlin Anal,2005,63:601-617.
[20] SU H,LIU L,WU Y.Positive solutions for a nonlinear second-order semipositone boundary value system[J].Nonlin Anal,2009,71:3240-3248.
[21] GUSTAFSON G B,SCHMITT K.Nonzero solutions of boundary value problems for second order ordinary and delay differential equations[J].J Differ Equ,1972,12:129-147.

