二维计算动词元胞网络形成模式的整体空间频率分布

王志刚

(中国神华神东煤炭集团设备维修中心，内蒙古伊金霍洛旗017200)

20世纪30年代，计算机之父阿兰·麦席森·图灵提出了“图灵机”模型，能够由一定输入得到一定输出.之后人们发现，只要设置好合适的输出输入的格式、内部状态以及控制程序，几乎现实中的所有计算，都能用图灵机来计算.50年代，计算机科学的另一个开创者冯·诺伊曼开始从计算的视角思考生命的本质问题，他认为自我复制乃是有生命的物体的独一无二的特征，也是被称之为生命的必要条件.为了构造一个能够自我复制的机器，冯·诺伊曼提出了元胞自动机的概念.后来剑桥大学数学家约翰·何顿·康威进一步证明了元胞自动机具有通用图灵机的计算能力，与图灵机计算等价.

计算动词元胞网络(CVCN)是一种建立在基于计算动词局域规则上的新型的元胞网络(T.Yang，2009).与其他元胞网络相比，如元胞自动机(Eric Goles and Servet Martinez，1994)和元胞神经网络(L.O.Chua and L.Yang，1988)，CVCN更为复杂且类型更多，更能体现语义学的作用，适合于复杂现象的建模.

二维计算动词元胞网络(2D－CVCN)是CVCNs中的一个重要部分，目前还处于探索阶段.Kun Wen and Tao Yang(2010)对二维计算动词元胞网络中形成的常见模式及一些罕见模式作了系统性的研究和分类，给出大量实验数据，说明CVCN很可能拥有模式形成的普遍性.换句话说，CVCN拥有与图灵机等价的计算能力.Wen Kun，Yang Tao(2010，Wen Kun et al.)提出了一些罕见的模式，比如图灵班图、游动的鱼、波传图、靶波等.

本文通过2D－CVCN的大量仿真实验，得到仿真结果，并且系统性地探究了二维计算动词元胞网络空间频率分布普遍性，证明二维计算动词元胞网络的邻域规则尚有可以改进的空间.

1 二维计算动词元胞网络

元胞网络可以被看作一种空间、时间、状态都离散的动力学系统.系统的状态变化由模型所定义的非线性特性所决定.这些变化往往极其复杂，不容易在数学上被证明.二维计算动词元胞网络以计算动词规则为局部规则，在设计和应用上十分简单，却能产生丰富的模式形成表现.常见的二维计算动词元胞网络的空间图谱结构是一张上下、左右相互连接的网络，可以被看作三维的圆环空间拓扑结构，如图1所示.

图1 二维计算动词元胞网络的拓扑结构

1.1 计算动词的定义(杨涛，2011)

可以用以下函数定义一个连续时间的计算动词V，

其中，TR并且ΩRn，T和Ω分别代表时间和状态空间.

类似地，可以用以下函数定义一个离散时间的计算动词V.

由计算动词的数学定义可见其易于操作，并涵盖了时间、状态以及状态进化三元素，其执行性高.

1.2 计算动词相似度

对于给定的模板计算动词V和一个观察所得的时间序列{x(t)}，用计算动词相似度(简称动词相似度)S(V;{x(t)})的方法来度量观察到的时间序列与模板计算动词的进化函数有多相似.如果取得了计算动词V1进化函数的一个实现的时间序列，那么S(V;{x(t)})可以被改写为S(V;V1).

尽管动词相似度有许多计算方法，但目前还没找到一个有关动词相似度的定义能够符合对计算动词之间相似度的所有直观感受.因此，动词相似度中存在着各种不确定性.例如，分别计算两个计算动词对于第三个动词的相似度，当同时使用一种计算方法时，可能得到相同的相似度，而同时使用另一种相似度计算方法时，它们的相似度却不同了.下面构造一种理想函数来表示计算动词相似度.已知的模板计算动词的生命周期有两个关键点:始点和终点.模板动词的进化函数表示如下

对于开始观察的动词 V=(0，Δx)，选取标准动词为 V={increase，decrease，stay}.

定义如下的计算动词相似度:

其中 Δ ＞0，κ ＞0，Δx=x(k)－x(k－1).

1.3 二维计算动词元胞网络的动词规则

2D－CVCN中元胞的初始状态通常是以随机的方式给定的，可以将此处于初始状态时的元胞称为第0代元胞.任意元胞与其相邻的元胞之间互相影响，影响的效果由计算动词规则及相邻元胞的动态变化规律共同确定.常见的二维计算动词采用3×3的摩尔邻域作为局部区域.

整体的动力学系统的动词规则由下式给出:

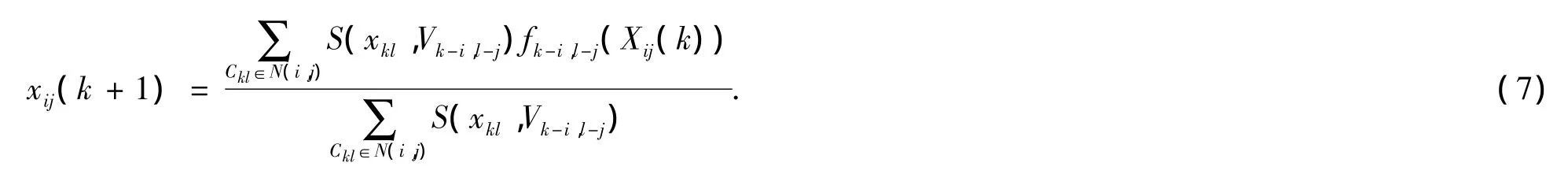
其中，由 S(xkl，Vk－i，l－j)计算动词的相似度函数，用来计算时间状态序列{xkl}与计算动词 Vk－i，l－j之间的相似程度.具体的相似度计算由动词规则确定.

在式(7)中，fk－i，l－j(xij(k))表示邻域元胞Ckl对中心元胞 Cij的作用或影响函数，定义

fk－i，l－j(xij(k))=gp·f(xij(k)).(8)

其中gp是模拟动词影响的参数，来衡量每个动词的影响程度，因为有3个标准动词，所以gp有3个值，定义如下式

其中，pi∈ R，ps∈ R，pd∈ R.

在式(8)中，f(xij(k))是非线性饱和输出函数.

由式(8)，(9)和(10)可知，每个元胞的第k+1代的状态，直接相关的是该元胞的前一代，即第k代的状态值的函数.而周围邻域元胞的影响，是在这个函数上乘以一个表示影响程度的系数因子.

2D－CVCN动词区域规则可以直观地由下式给出.

每个中心元胞的状态与它所在邻域所选取的动词规则有关，动词规则的设定很大程度上决定了将会形成的模式，定义矩阵A为动词规则矩阵，即

由于我们选取了3个标准动词，所以总共将有39=19683种可能的规则，考虑到对称性，可能性空间会有所减小，但仍然是一个很大的数字.我们将取其中最常见的一组动词规则进行系统分析.而在每组规则下，不同的pi，pd，ps以及相似度函数中Δ，κ的参数值的选取不同，也可能得到完全不同的实验结果.

2 实验

首先预定义动词规则矩阵为以下动词规则矩阵:

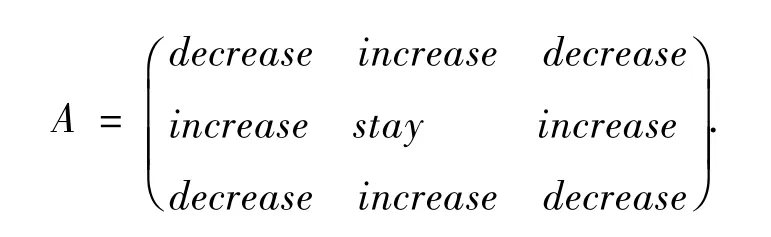
设置网络大小为160×160，相似度计算参数Δ=0.5和κ=1.我们采用遍历参数空间的方式，对这个规则矩阵下的模式进行系统性的探究.动词影响参数的取值通过均匀等距离取点的方式遍历给定参数空间，pi，pd，ps∈(－10:0.2:10).每一次改变参数就进行一次实验，一共进行1003次实验.每次实验对网络中所有元胞的初始状态值取［0，1］区间内的随机值，根据局域动词规则进行全网同步跟新.让其自由进化到1000代，记录此时的网络状态作为实验数据保存.将实验结果用HSV颜色空间表示，可视化后效果如图2所示.

图2 二维计算动词元胞网络生成的多种多样的模式

观察实验结果，我们发现1000000实验有642308次得到同质模式(homogenous pattern)，出现的概率为64.23%.用符号＆(y，x)代表图2中第y行第x个.我们发现高频模式(例如条纹图形、棋盘格图形)常常伴随着线条 ＆(1，4).在单向高频下，方块被挤压，可以对比 ＆(1，2)、＆(6，2)、＆(7，5).线条可能隔离两种不同的模式＆(6，1)、＆(7，2).由于篇幅有限，这里不作太多解释.

通过将实验遍历和迭代形成的模式进行傅立叶变换，并将除了同质模式以外的357692个网络状态的频谱累加，得到图3中的频谱统计.可以看出，整体的空间频率分布集中在中心最低频及水平方向(上下端的中间)、垂直方向(左右端的中间)和双向最高频率(四角)附近.这说明2D－CVCN在方形的摩尔邻域下倾向于最低频模式和最高频模式的形成.

图3 对二维计算动词元胞网络357692次实验结果的网络频谱能量分布统计

3 结语

综上所述，我们通过对2D－CVCN的等间隔参数空间遍历，得到海量的形成模式，并对这些模式的频谱进行统计.从统计结果可以看出，2D－CVCN得到的模式空间频率集中分布在最低频和3个极高频附近，能量向外围渐减.由此可以推断摩尔邻域很可能是限制2D－CVCN成为通用模式形成工具的一个瓶颈.此外，我们还发现同质模式出现的频率约为64.23%.

［1］T.Yang.Computational verb cellular networks:Part I－ A new paradigm of human social pattern formation［J］.International Journal of Computational Cognition，2009，7(1):1 －34.

［2］T.Yang.Computational verb cellular networks:Part II－ One－dimensional computational verb local rules［J］.International Journal of Computational Cognition，2009，7(1):35 －51.

［3］T.Yang.Computational verb cellular networks:Part III－ Solutions of one－dimensional Computational verb cellular networks［J］.International Journal of Computational Cognition，2009，7(2):1 －11.

［4］Eric Goles and Servet Martinez.Cellular automata，dynamical systems，and neural networks［M］.Kluwer Academic Publishers，1994.

［5］L.O.Chua and L.Yang.Cellular neural networks:Applications［J］.IEEE Transactions on Circuits and Systems，1988，35(10):1273－1290.

［6］Kun Wen and Tao Yang.Classification of Patterns Formed in Two－Dimensional Computational verb Cellular Networks［J］.International Journal of Computational Cognition，2010，8(4):1 －37.

［7］Kun Wen，Tao Yang.New patterns in two－dimensional computational verb cellular networks［C］.International Conference on Anti－Counterfeiting，Security and Identification(ASID)，2010:219 －222.

［8］Kun Wen，Xuezhi Wu，Tao Yang.Diffusion and wave propagation patterns in computational verb cellular networks［C］.Proceedings of the International Conference on Anti－Counterfeiting，Security and Identification(ASID)，2012:24 －26.

［9］杨涛.计算动词理论及应用［M］.厦门:厦门大学出版社，2011.