基于小波分析AR（P）-SVR组合模型在大坝变形预测中的应用

基于小波分析AR(P)-SVR组合模型在大坝变形预测中的应用

沈哲辉，黄腾，邱伟，郑浩

(河海大学地球科学与工程学院，江苏南京210098)

摘要：监测序列经小波分解后，得到低频分量和高频分量。对低频分量采用自回归AR(P)模型预测，对高频分量采用支持向量回归机SVR模型预测，最后将各分量进行小波重构，得到监测序列的预测值。结果表明，此种预测方法比直接使用SVR模型或经小波分解后再采用SVR模型预测精度高。

关键词：小波分解；AR(P)模型；SVR模型；小波重构；预测

中图分类号：TU196

收稿日期：2014-04-30;修回日期：2014-11-23

作者简介：沈哲辉(1991-)，男，硕士研究生.

ApplicationofAR(P)-SVRcombinationmodelbasedonwaveletanalysisindamdeformationpredictionSHENZhe-hui,HUANGTeng,QIUWei,ZHENGHao

(SchoolofEarthSciencesandEngineering,HehaiUniversity,Nanjing210098,China)

Abstract：Low frequency and high frequency components are obtained through wavelet decomposition.The low frequency components are adopted in the AR(P) model to make predictions, while the high frequency components make predictions with SVR model. Then the predicted data after reconstructing them are obtained.Results show this model has higher prediction accuracy than SVR model without wavelet decomposition and the model that only uses SVR to predict each component after wavelet decomposition.

Keywords：waveletdecomposition;AR(P)model;SVRmodel;waveletreconstruction;prediction

大坝变形预测的方法有灰色模型法、自回归模型、神经网络等。但由于大坝变形受影响因素多，组合模型的应用使大坝变形预测精度有了提高[1-4]。

小波变换是一个时间和频率的局域变换，能有效地提取信号，通过伸缩和平移对函数或信号进行多尺度分析[5]，并且小波分解后的平稳性比原信号好的多。支持向量机是一种新兴机器学习方法，克服了神经网络的过拟合、收敛速度慢、容易陷入局部极值等缺点，被公认为是人工神经网络的替代方法[6]。小波分解后的低频分量，用线性自回归模型预测，而高频分量仍用SVR预测模型，重构后相比低、高频分量使用SVR预测精度颇为理想。

1建立组合模型

1.1小波分解

利用Mallat算法，首先将离散的大坝监测数据分成高频部分d1和低频部分c1，然后再把低频部分c1进一步分解，重复以上过程可以得到任意分辨率下的高频和低频部分。具体算法[7]：

(1)

(2)

式中:j=1,2,…，J-1为分解尺度;k，n为平移系数；Cj+1,k，Dj+1,k分别为在2j分辨率下的低频近似分量系数和高频细节分量系数；gn-2k，hn-2k分别为高通滤波系数和低通滤波系数。

式中:ψ(x)为小波函数，φ(x)为尺度函数。

利用分解后的小波系数可重构原来的序列小波重构的Mallat算法为

(3)

监测序列经小波分解后，其低频分量用自回归AR(P)模型进行见面预测，高频分量用支持向量回归机SVR模型进行建模预测。

1.2自回归AR(P)模型

AR(P)模型称为自回归模型，由于该模型在建模时只需解线性方程组，而又不涉及白噪声序列值，计算简便，所以在时序分析中，AR(P)是采用最多的一种模型[8]。AR(P)模型表示为

(4)

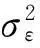
本文采用FPE定阶准则，即最小最终预报误差准则对p定阶，回归系数采用最小二乘法求得。

1.3支持向量机模型

在20世纪90年代，Vapnik提出支持向量机是数据挖掘中的一项新技术，是借助于最优化的方法解决机器学习问题的新工具，它是一种以结构风险最小化原则为基础的机器学习算法，通过寻找一个线性约束的二次规划问题得到全局最优解，因而不存在局部极小值的问题，快速算法保证了收敛速度[9]。

支持向量回归机(SupportVectorRegression，SVR)是支持向量在函数回归领域的应用。支持向量回归机首先考虑用线性回归函数

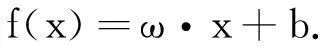
(5)

拟合(xi,yi),i=1,2,…,n；xi∈Rn为输入量，yi∈R为输出量，即需要确定ω和b。在非线性的情况下，通过一个非线性映射将数据映射到高维特征空间中，并在这个空间进行线性回归。需要引入核函数K(x,xi)代替内积运算。常用的核函数为

1)多项式核：K(x,xi)=(x,xi+1)d，d为阶数；

3)感知器核：K(x,xi)=tanh(βxi+b)。

本文采用的核函数为径向基RBF核函数(高斯核函数)。RBF核函数是一个普通的核函数，通过参数的选择，适用于任意分布的样本，因此RBF核

函数是目前支持向量机中被应用最广泛的一种核函数[10]。选择合适的损失参数ε和惩罚参数C，构造高维特征空间中求回归问题：

(6)

(7)

得到非线性回归函数为

(8)

本文采用网格法寻求最优的损失参数ε和惩罚参数C。

1.4小波分解下的AR(P)-SVR组合模型

本文构建小波分解的AR(P)-SVR组合模型。

1)将监测序列进行小波分解，小波函数选用Daubechies系列小波函数db3。将监测序列分解为2层，并进行单支重构，得到低频分量a2和高频分量d1，d2。

2)用自回归AR(P)模型对低频分量进行预测，得到拟合值和预测值。

3)用支持向量回归机SVR对各层高频分量进行建模并预测。对每个高频分量，分别构建一个多输入、单输出的支持向量回归机预测模型[11]。

4)小波重构，将用AR(P)模型预测后的低频分量和用SVR建模预测后的高频分量进行小波重构，得到监测序列的拟合值和预测值，建模流程如图1所示。

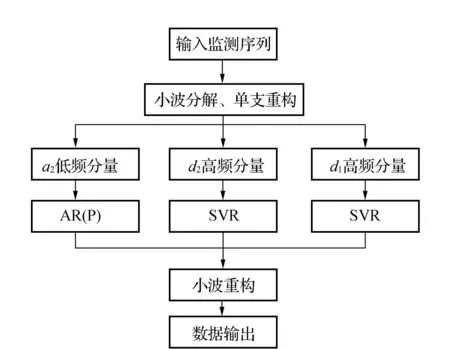
图1　建模流程

2实例分析

本文采用福建省某大坝的50期顺河向水平位移观测数据，利用前45期数据建模，并预测后5期，用后5期数据检验预测的准确性。

本文采用紧支撑正交小波db3小波进两层小波分解。在对低频分量a2进行AR(P)建模时，采用FPE定阶准则，最后确定阶数为4阶。对高频分量d1和d2进行SVR建模时，根据经验，取输入量维数为5，采用网格法寻找最优参数。图2为a2的自回归模型拟合及预测曲线，图3为d2支持向量回归机拟合及预测曲线，图4为d1支持向量回归机拟合及预测曲线。

图2　a 2的自回归模型拟合及预测曲线

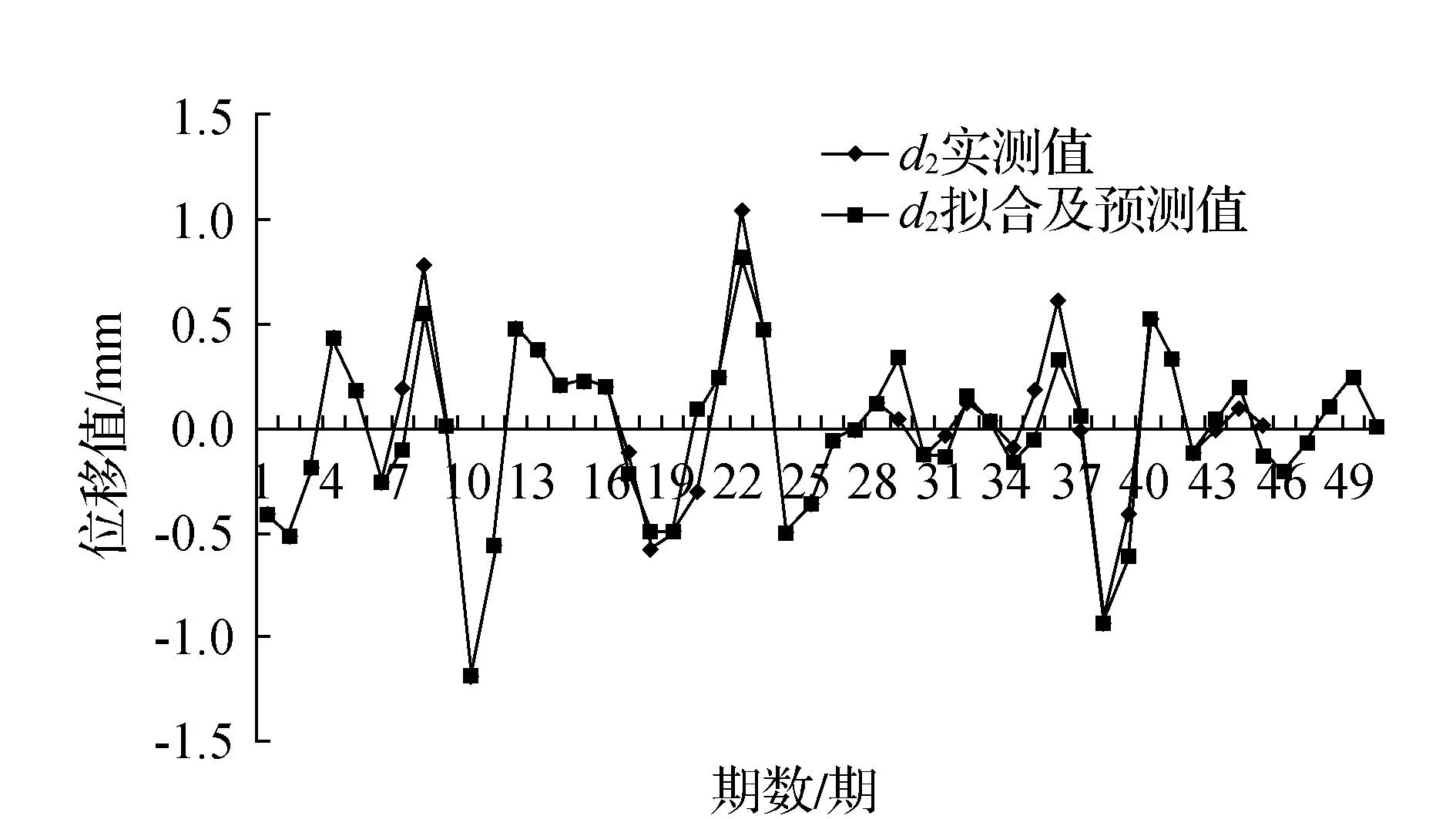
图3　d 2的支持向量回归机模型拟合及预测曲线

图4　d 1的支持向量回归机模型拟合预测曲线

得到各个分量的拟合值和预测值后，再进行小波重构，根据S=a2+d2+d1进行重构，得到最终的拟合值及预测值，并将5期的预测值与后5期的实测值进行对比，用相对误差衡量预测精度。为验证本文模型(模型1)的预测效果，对比使用SVR模型预测(模型2)的精度和经小波分解的各分量都采用SVR模型预测(模型3)的精度。各模型预测结果比较见表1。

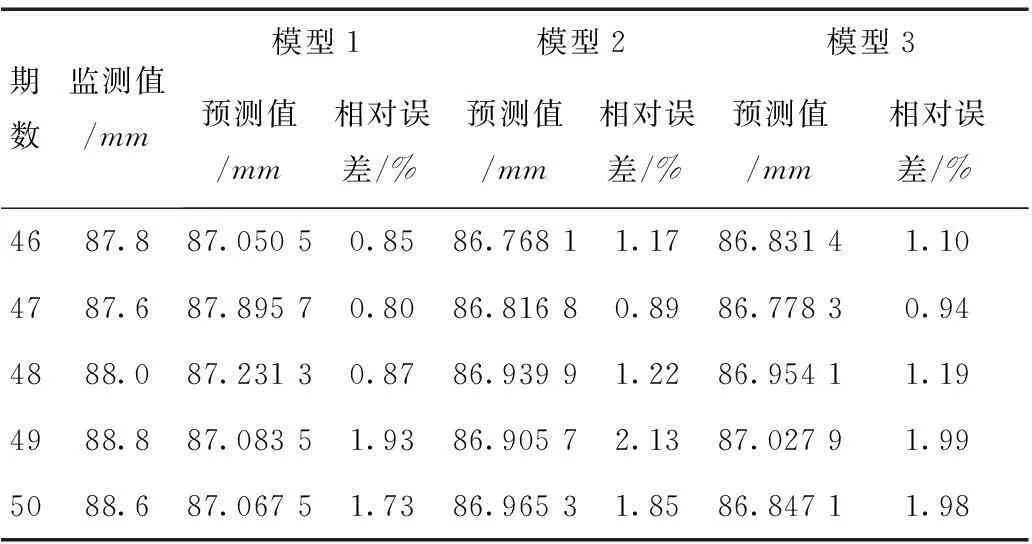
表1　预测结果比较

由表1计算可得，模型2(SVR)的预测值相对误差的平均值为1.45%，模型3(W-SVR)的预测值相对误差的平均值为1.44%，可见模型3预测精度比模型2的预测精度有提高，但不明显。本文建立的组合模型，即模型1的预测值相对误差的平均值为1.24%，可见本文的组合模型预测效果明显比其他两种模型的预测效果好。

3结束语

本文将小波分析、自回归AR(P)模型和支持向量回归机SVR结合在一起，构建用于预测大坝变形的组合模型。通过小波分解，将低频分量和高频分量分别用自回归模型和支持向量回归机模型建模预测、重构。经实验发现，监测序列经小波分解后，相比SVR,其低频分量更适合用自回归模型建模预测。小波重构后，本文构建的组合模型的预测精度相对于经小波分解的各分量都采用SVR模型预测的精度高。

参考文献：

[1]王新洲,范千,许承权,等.基于小波变换和支持向量机的大坝变形预测[J].武汉大学学报：信息科学版,2008,33(5)：469-471.

[2]郭锴，陈伟清，文鸿雁，等.非等时距灰色线性组合模型在变形监测中的应用[J].测绘科学，2014,39(7)：131-135.

[3]简伶俐，罗志清，赵福洪.基于二次平滑和指数曲线的串联式组合模型在沉降预测中的应用[J].测绘工程，2014,23(9)：45-47.新洲,范千,许承权,等.基于小波变换和支持向量机的大坝变形预测[J].武汉大学学报：信息科学版,2008,33(5)：469-471.

[2]郭锴，陈伟清，文鸿雁，等.非等时距灰色线性组合模型在变形监测中的应用[J].测绘科学，2014,39(7)：131-135.

[3]简伶俐，罗志清，赵福洪.基于二次平滑和指数曲线的串联式组合模型在沉降预测中的应用[J].测绘工程，2014,23(9)：45-47.

[4]唐佑辉，黄腾，赵兵帅.GOM和时间序列组合模型在地表沉降预测中的应用[J].测绘工程，2014,23(2)：70-72.

[5]胡晓虎.基于小波-BP神经网络的风电场短期风速预测[J].铜陵学院学报,2012,11(4)：107-109.

[6]崔艳,程跃华.小波支持向量机在交通流量预测中的应用[J].计算机仿真,2011,28(7)：353-356.

[7]刘新东,陈焕远,佘彩绮.基于小波阀值降噪和BP神经网络的超短期风电功率预测[J].世界科技研究与发展,2011,33(6)：1006r1010.

[8]郝少峰，方源敏，杨建文，等.基于熵权法的组合模型在滑坡变形预测中的应用[J].测绘工程，2014,23(7)：62-64.

[9]唐亮贵,程代杰.基于小波的支持向量机预测模型及应用[J].计算机科学,2006,33(3)：202-204.

[10]唐争气，谭志强.灰色时序组合模型在基坑监测中的运用[J].测绘工程，2014,23(2)：49-53.

[11]黄惠峰，张献州.高速铁路沉降变形的组合预测方法应用[J].测绘工程，2014,23(9)：48-51.

[责任编辑：李铭娜]