订单波动下的发动机销售预测
订单波动下的发动机销售预测
徐炜
(上海交通大学机械与动力学院,上海200240)
摘要在当今日益变化的发动机市场环境下,竞争日趋激烈,订单常常发生波动。如何在订单波动下预测发动机的销售量,以合理安排生产,是企业管理面临的一个挑战。但预测方法会影响预测的准确性,对3种预测方法及其预测误差进行了比较和分析。以某发动机制造厂为例,说明如何根据订单波动情况,预测发动机的销售量。
关键词:发动机订单波动销售预测
来稿日期:2015-03-12
1 前言
改革开放30多年来,中国经济取得了突飞猛进的发展。随着经济建设的快速发展,特别是基础建设,发动机行业为适应形势发展,各厂家纷纷采用先进的国际技术、先进的制造工艺和设备、进行大幅度的生产改造,大幅度提高了制造能力和产品技术水平。现在,大部分发动机制造商都采用柔性生产线,具备了小批量、多品种的生产能力。
同时,发动机市场激烈竞争也越发激烈,导致市场需求不断发生变化。订单波动势必对组织节能型的生产造成很大困难,因而根据订单波动尽可能相对准确地预测发动机的销售量,是各企业能应对市场需求变化,做到合理安排生产的重要措施之一。
预测的精确程度取决于预测误差大小。不同的预测方法,误差不同;用于不同领域,误差也不相同。通过选择预测方法将误差降至最低是预测研究的目标。根据以往订单波动情况,相对精确地预测发动机销售量是本文探讨的目的。
2 预测方法选择
2.1预测的概念
企业所处的环境不断在变化,全球化的发展趋势、新技术的推广应用、互联网资源的广泛使用,使得企业所处的环境更加复杂,变化的频率也更快,这些给企业预测市场需求带来新的挑战。首先要根据产品特性、生命周期和以及目前所处的阶段,确认采取何种预测方法。选择适合本企业产品和市场的预测方法,可提高预测的准确率。
预测方法的选择是预测的重要工作。随着预测方法的不断发展,对于预测关注的重点就集中在预测方法固有的误差,并尽可能地使这种不可避免的误差降至最低。
2.2预测的方法
通常,预测方法可以分为定性预测和定量预测2种。定性预测注重于趋势的发展,适用于宏观的预测,但容易受人知识、经验和能力的约束和限制,产生偏差,同时难以作精确数量上的描述。定量预测注重于数量变化的分析,常用于企业短期需求预测等方面,需要准确的数据作支撑,对不可预知、难以量化的影响因素,缺乏自适应能力。在实际工作中,往往将这2种预测方法组合使用[1, 2]。
定性方法主要依赖于人的主观判断。在无法获取或只能获取很少历史数据的前提下,且某类人(如专家、特殊市场的销售人员)对市场的见解非常重要时,经常采用定性方法。具体方法有德尔斐法、主观概率法、领先指标法、厂长(经理)评判意见法、推销人员估计法、相互影响分析法、情景预测法等。
定量方法是使用一些历史数据、或因素变量来预测需求的一种数学模型。是根据已掌握的比较完备的历史统计数据,运用一定的数学方法进行科学加工整理,借以揭示有关变量之间的规律性联系,用于预测和推测未来发展变化情况的一类预测方法。其主要特点是利用统计资料和数学模型来进行预测。然而,这并不意味着定量方法完全排除主观因素,相反主观判断在定量方法中仍起着重要的作用,只不过与定性方法相比,各种主观因素所起的作用小一些。目前主要的定量预测方法有:时间序列分析、因果关系和仿真法。
时间序列方法:运用历史数据对未来需求进行预测。它依赖于一个假设,即过去需求是未来需求的指示器,通过分析周期性、趋势性和季节性影响,预测未来的需求。它是一种考虑变量随时间发展变化规律,并用该变量以往的统计资料建立数学模型,作外推的预测方法。
因果法:是根据事物之间的因果关系来预测事物的发展和变化。通过对需求预测目标有直接、或间接影响因素的分析找出其变化的规律,并根据这种变化规律来确定预测值。由于反映需求及其影响因素之间因果关系的数学模型不同,又有各种分类。
仿真法:运用各种模型和技术,对实际问题进行建模,通过动态模拟的方式进行仿真实验。通过仿真,进行各种方案的比较,以求得最优解,进而运用在实际工作中。
其中时间序列法因其数据收集方便、计算相对简单、短期预测准确率较高而广泛应用于各个行业。影响时间序列的因素,根据因素特点和影响效果分,主要有长期趋势、季节变动、循环变动和不规则变动[1]。
从影响因素作用的大小和方向变化的时间特性分析,时间序列法具有4个特点:趋势性、周期性、随机性和综合性。
(1)趋势性:某个变量随着时间的推移或自变量变化,呈现一种缓慢而长期的持续上升、下降、持平的变化趋势,但变动的幅度可能有差异。
(2)周期性:某因素因外部影响,随着自然季节的变化而出现高峰、低谷的相对固定的规律。
(3)随机性:单个变量在短时间内体现出随机性,但长时间的整体统计体现出规律性。
(4)综合性:实际情况往往是多种因素各自发生变动后综合作用叠加的结果。所以,预测时,需要过滤不规则变动,突出显现的趋势性和周期性。
根据对资料分析方法的不同,时间序列法又可以分为:简单时序平均数法、加权时序平均数法、移动平均法、加权移动平均法、趋势预测法、指数平滑法、季节性趋势预测法、市场寿命周期预测法。下面介绍主要几种方法。
2.2.1移动平均法
对需求序列的均值进行估计,消除随机波动的影响,计算前n期的均值,并把它作为下一期需求的预测值;随着时间的推移,会有新的数据加入,预测值也会随之改变。

式中,
Xt——t时期的实际观测值;
n——计算平均值所用的总期数;
Ft+1——t +1时期的预测值。
移动平均法可根据需要,使用尽可能多时期的数据。使用的时期越多,越可以得到更稳定的预测值;而使用的时期越少,预测值的灵敏度更高。当需求变化相对不频繁时,尽可能使用较多时期的数据;当需求波动较大时,应该使用较少时期的数据。在实际预测时,需要在稳定性和灵敏性之间权衡,根据需要选择。同时,因每个时间节点的权重是相同的,所以,无法重点突出需要加倍关注的时间节点。
2.2.2加权平均移动法
根据需要给每个时期赋予不同的权重,所有权重之和等于1。可以考虑赋予近期数据比较大的权重,远期数据比较小的权重;也可以考虑给关键时期数据比较大的权重,以体现其重要性。

式中,
滋t——第t期的权重系数;
Xt——第t期的实际观测值;
注意:滋1+滋2+…+滋t-1+滋t=1。
加权移动法对近期的观测趋势较为敏感。但如果一组数据有明显的季节性影响时,采用加权移动平均法所得到的预测值,可能会出现偏差。因此,有明显的季节性影响因素存在时,最好不要采用加权法[3]。
2.2.3指数平滑法
指数平滑法为先前所有的观测值提供了指数加权移动平均值,且根据最近的经验对估算值不断修正,越近的观测值权重琢越大,以指数递减的方式琢(1-琢)n类推,新的观测值可以被看作是最新观测结果和前一期观测值的加权总和。指数平滑法有简单指数法、Holt指数平滑法和Winters指数平滑法。
(1)简单指数法:也称一次指数平滑法,计算公式如下。
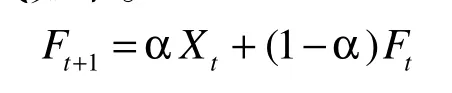
式中,
Xt——最新观测值;
Ft+1——下一期预测值;
琢——平滑常数,取值范围(0~1)之间。
简单指数平滑法不需要太多的历史数据,就可以进行分析预测;极端情况下只需要一个最新观测值、一个最新预测值和琢值就可以进行预测。它直观地体现了水平波动,但无法进行趋势、季节上的预测。平滑常数琢是权重系数。当琢的取值越大,最新的预测值就趋近于当前观测结果,体现变化的速度越快;当琢的取值越小,最新的预测值就类似于以前的预测值,体现变化的速度越慢[3]。
(2)Holt指数平滑法:不直接应用一次指数平滑值进行计算,主要是分别对原序列St和序列的趋势bt进行平滑处理。它使用2个平滑参数,分别用琢和茁表示,取值范围为(0~1)之间。Holt指数平滑法公式如下。
起始值:S1=X1,b1=X2-X1,也可以按照b1=[ (x2-x1)+(x3-x2)+(x4-x3) ]/3计算。
Holt指数平滑法通过更新指数平滑序列或现时水平估算值,计算趋势估算值,进而来预测未来一段时间内的预测值。它充分考虑了整个时间序列上的发展趋势。
平滑常数琢和茁的取值,对预测结果有很大的影响,通常需要选择几组数据进行分析比较。虽然Holt平滑法考虑了时间上的趋势变化,但对于一定时间段内的周期性变化,则无法进行预测[3]。
(3)Winters指数平滑法:在Holt指数平滑法的基础上增加季节变化系数,充分考虑了时间、趋势和季节的多重影响因素,是Holt指数平滑法的扩展。
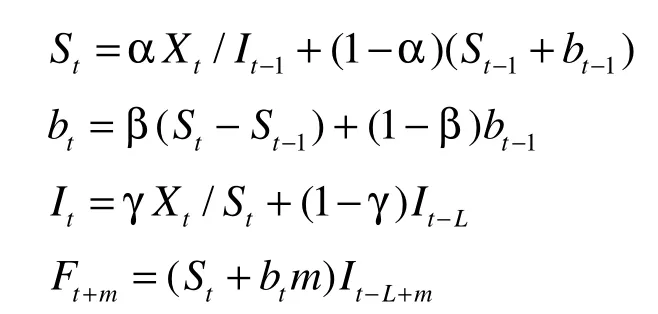
其中,L为季节的长度,I为季节修正系数,m为季节因子选择值。
Winters指数平滑法通过更新现时水平估算值,来计算趋势、季节性的估算值,进而计算出未来一段时间内的预测值。相对于Holt法,它增加了时间序列季节性变动或周期性变动的分析和预测,可以同时处理趋势和季节变化,并能将波动的影响适当地去除,特别适用于包含趋势和季节变化的时间序列问题[4]。
2.3预测方法中误差的测定
任何预测都会有误差,与实际值或多或少存在偏差。如何选择最佳的预测方法,只能通过实践中得到。在一段时间内采用不同方法进行一系列预测,并进行检验和评定,选出偏差最少的预测方法。t时期实际值与预测值之差为Et=Xt-Yt,通常采用累积误差CFE进行简单评定。
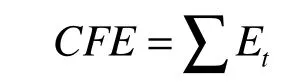
正负误差会在CFE计算中相互抵消,但它有助于发现一致性偏差。
每一时期实际值与预测值之差通常称为余数:

et——时间周期t内的预测误差;
Yt——时间周期t内的实际值;
Yt——时间周期t内的预测值。
大多数时间,都是通过预测值与实际值之差的某种函数的平均值,来判定预测的准确率。常有以下4种评定方法。
(1)绝对平均偏差MAD评定:通过预测误差数值的平均值来衡量预测的准确率。MAD值越小,说明预测值非常接近实际值,即预测很准确。而MAD值较大,则说明存在很大的预测误差。
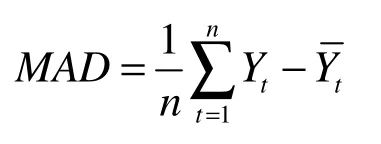
(2)均方误差MSE评定:求出每个余数或误差的平方,然后将它们相加,并除以所得结果的个数。因经过平方,使那些较大的误差变得更大,更有助于判定偶然误差。与MAD一样,MSE值越小,预测越准确,MSE值越大,则预测误差越大。

(3)绝对平均百分比误差MAPE评定:通过查找每一时期的绝对误差,并用该时期的实际观测值相除,求得绝对百分比误差,然后求其平均值。与MAD和MSE的主要差别在于,MAPE可以对基于两组不同数据的预测进行比较。
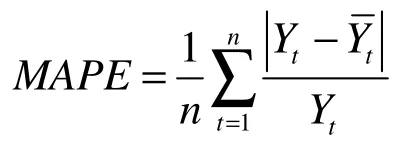
(4)平均百分比误差MPE评定:通过查找每一时期的误差,再用该时期的实际值相除,然后得到这些百分比误差的平均值。根据结果来判定预测方法的准确性。当MPE值非常接近零时,证明该预测方法非常准确;而当MPE值是一个大百分比负值时,说明该预测方法评价过高;当MPE值是一个大的正数时,说明该预测方法评价过低。

在生产实际工作中,人们经常同时使用以上4种方法来判定预测的效果。比较2种或2种以上不同方法的准确度,测定某种方法的适用性及可靠性,有助于寻找最佳的预测方法。根据实际需求,可侧重于某一种或两种方法的误差数值,对其系数的取值进行修正和完善,以寻找最佳的方法。
2.4预测方法的选择
对于各种不同的预测方法,都有其自身的优势和适用范围。如何选择合适的预测方法,就成了预测工作的重要内容。一般来讲,可从以下几个方面来考虑。
(1)预测对象与目的:根据产品特性、生命周期和目前的阶段,确认采取何种预测方法。快速消耗品,一般采用短期预测;机械产品,因价格因素,一般使用周期较长,往往采用长期预测。同样,对于产品处于生命周期的不同阶段,也会采用不同的方法,在试销期,一般采用定点实验的方法;而在产品的稳定期,往往采用简单的加权平均法;如果有季节的特性,也会使用有季节变动的温特法等。
(2)根据已有的信息:如果自己掌握的信息、资料、数据比较充分、全面,就可以选择相对复杂点的预测方法,以期通过较多的数据得到相对准确的预测结果。如果掌握的信息量很有限,则可以采用相对简单但有效的德尔菲法、评判法等。
(3)根据数据特性:如果历史数据的趋势相当平稳,可以选择简单平均、加权平均法;如果数据表现出明显的线性趋势,则采用移动平均法、时间序列法、线性回归法;如果数据出现明显的非线性趋势,则采用指数增长方法。所以,需要对预测使用的数据进行深入的分析后,再选择预测方法。
(
4)从企业实际情况出发:不同的预测方法会产生不同预测效果和费用。当不需要精准的结果时,就没有必要花费较多的人力、精力去收集数据进行分析、预测,只需要少量的数据进行相对简单的预测即可。同样,也可以根据所需要结果来确定方法,进而控制预测过程中的费用,用最少的费用达到最大的效果。
综上所述,在确定需要对产品销售量进行预测时,首先需要对产品的特性及所要达到的目的进行明确,再分析预测所需要的信息、数据量及趋势,结合企业实际情况,所需要的精准度和所能付出的费用,确定最终的预测方法[5]。
3 预测方法的应用
某发动机制造企业是典型的老国营企业转型,早期受原有体制的约束,发展比较缓慢,但在残酷的市场竞争中,也不断地进行着探索。对于生产运营系统的改造和完善,从未间断过,无论是从组织架构、零部件的布点,还是工艺流程,都在进行适应性的改造。自2008年经济危机爆发以来,产能从不足到过剩,促使公司管理层对于生产运营系统的改进和优化,以适应当前形势的发展。
面对市场激烈的竞争,销售订单也随着经济形势而上下波动。公司一直在摸索如何根据订单变化,相对精确地预测未来的销售量,以做到生产计划和安全库存储备合理。本节根据第2节的理论依据,根据该公司的实际情况,尝试分别采用比较分析移动平均法、简单指数平滑法和Winters指数平滑法,为该公司预测销售量。
发动机的销售具有一定的趋势性和季节性。趋势性与国家宏观形势、经济环境、所属行业发展规律以及本企业的营销策略有关;而季节性主要是所属行业的习惯性销售,一般年初与9、10月份属于销售旺季。这里取2010年1月至2014年10月共58个月里,某型号发动机的销售数据作为样本数进行计算和分析。图1是营销预测值与实际销售量的比较。从图中可以看出,预测量与实际销售量还是有比较大的差异。个中原因很多,如:(1)客户的判断失误;(2)客户经理的市场预测不准;(3)季节性的变化等等,都会导致预测与实际的差异。

图1 营销预测值与实际销售量的比较
以上述数据为样本基础,分别用移动平均法、Holt指数平滑法和Winters指数平滑法,预测下一时间段的需求。
3.1移动平均法
先根据简单平均法对这一时期的销售进行预测。在计算初期,因发动机的季节性销售比较明显,所以n设定为3,从第4期开始预测,以此类推,可以求得第t+1期的预测值。图2为移动平均法预测值与实际销售量的比较。从图中可以看出,前期预测值低于实际销售量,且波动较大,中、后期则与实际情况比较接近。因样本数较大,对于近期的趋势反应不够明显,权重差异不能很好体现,对于季节性的趋势处理并不具有优势。
3.2简单指数平滑法
在计算开始时,设定初始值如下:Xt=X1=92,X2=90,F2=(X1+X2)/2=91,琢=0.2,则X3=0.2×90+(1-0.2)×91=91;以此类推,可以求得第t+1期的值。经过误差分析比较,选取最优值琢=0.6。
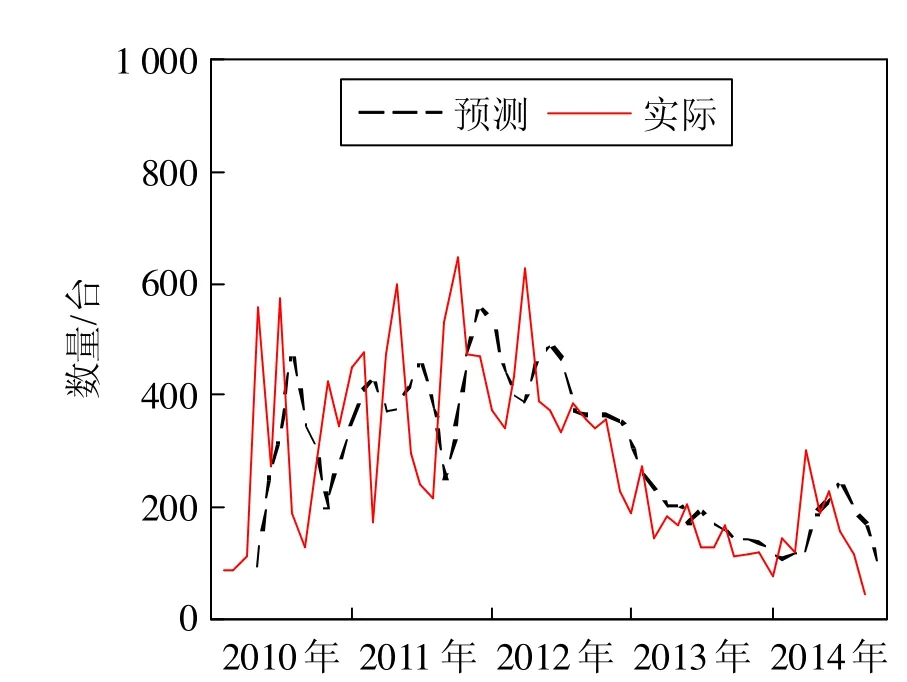
图2 移动平均法预测值与实际销售量的比较
图3是简单指数平滑法预测与实际情况的比较。从图中可见,简单指数平滑法的预测结果比移动平均法的更为准确些。因为它以指数递减的平均序列的历史数据为基础,将最近的实际销售数量赋予最大的权重,这样的预测往往贴近最近的销售趋势;但是,在数据的波峰、波谷处,预测值与实际销售量的差异就显得比较突出。可以通过琢值的选取来决定当期结果对下一期预测的影响程度。
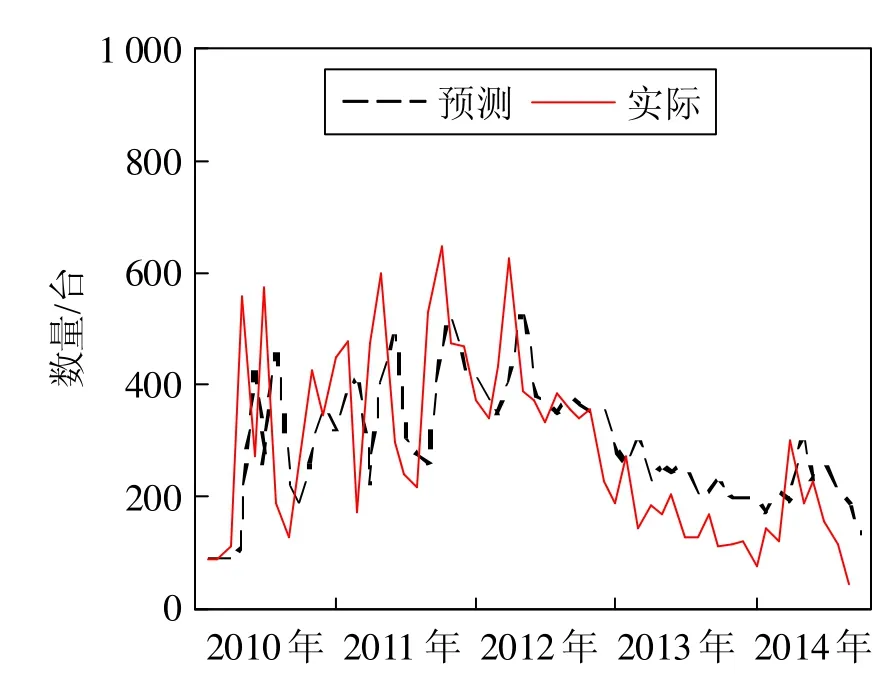
图3 简单指数平滑法预测值与实际销售量的比较
3.3 Winters指数平滑法
采用Winters指数平滑法,初值的设定可以将第1个预测值设置与第1个实际销售量相等,也可以通过将前n期的实际销售量回归计算,以取得初始值;而水平、趋势、季节平滑指数的选择,往往通过预测误差(如MSE)最小化来优化选取。
对前10期实际销售量回归,得到初始值:
S1=152.485,b1=21.528,I1=0.523
S2=177.914,b2=19.556,I2=0.612
S3=305.709,b3=3.024,I3=1.052
平滑指数初定为:琢=0.2,茁=0.1,酌=0.1,m取1。根据公式计算可得S4:

以此类推,可以求得第t+m期的F值。再通过对系数琢、茁、酌的优化分析,可求得最优的平滑系数:琢=0.5,茁=0.2,酌=0.3。
从以上的分析可以看出,Winters指数平滑法在需求波动的环境下,通过对趋势性、季节性的补偿修正,能相对准确地预测未来销售数量,如图4所示。

图4 Winters指数平滑法预测值与实际销售量的比较
上述3种方法的误差分析比较结果见表1。从表中可以看出,这3种方法中,Winters指数平滑法的预测误差最小,即预测与实际的差异最小;尤其与申报值比较,具有较高的准确性,故具有较高的指导意义。
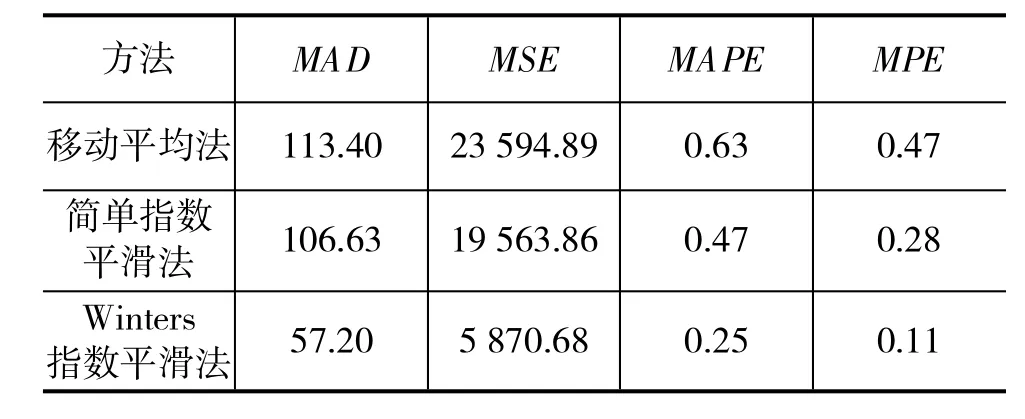
表1 误差分析对比
4 小结
(1)随着市场竞争的加剧,独立发动机厂家的市场生存越来越困难,但同时也存在着机遇。根据产品系列选择合适的配套市场,有选择地突破,也能独树一帜,寻找到适合自身企业的发展空间。
(2)针对配套市场的行业特点,科学地运用市场预测理论和预测方法,对企业产品的市场需求进行预测,才能在市场频繁变化、订单不断波动的环境下,针对特定市场,充分整合和运用有限资源,在激烈的市场竞争中求得生存和发展。
(3)根据科学预测并得到验证的市场需求,可以合理地设置产品安全库存,一方面避免产品的积压,另一方面避免市场变动时的供货不足;同时,可以根据预测数据,结合实际库存,合理、有效地安排生产。
(4)科学预测体系是一个渐进的过程,随着时间的推移,趋势会随之变化,数据的完整性、有效性;预测方法的科学选择以及及时调整都需要不断地完善。
在合理、有效的预测基础上,还需要充分地了解市场,掌握市场的动向,任何一点终端市场的微小变化,都会对中间产品产生非常大的影响。任何预测都不可能与实际情况完全一致,所要做的是将误差控制在最小范围内。将变化的因素充分考虑并加以筛选,提供最真实、有效的需求预测,并加强新产品开发、价格策略制定、售后市场的维护等方面的工作,企业就一定会在市场竞争中占得先机,不断提高市场占有率,并进一步寻求更大的发展。
参考文献
[1]威尔马L,恩博耶K.运营与供应链管理-理论与实践霍艳芳[M].李秉光,徐刚译.北京:清华大学出版社,2010.
[2]韦伯斯特S.供应链管理-原理与工具[M].蔡三发,邱灿华,王晓强译.北京:机械工业出版社,2009.
[3]乔普拉N,迈因德尔P.供应链管理[M].陈荣秋等译.北京:中国人民大学出版社,2008.
[4]王丽亚,陈友玲,马汉武.生产计划与控制[M].北京:清华大学出版社,2010.
[5]汉克E J,威切恩W D.商业预测[M].胡晓凤译.北京:清华大学出版社,2006.
Discussion of Engine Sales Prediction Under Fluctuated Market Demand
Xu Wei
(School of Mechanical Engineering of Shanghai Jiao Tong University, Shanghai 200240, China)
Abstract:In today's ever-changing market, market competition is becoming fierce, which leads to market demand fluctuation. To predict engines sales under fluctuated market demand for a good arrangement of engine production is a challenge facing engine manufacturers. With the help of data mining theory and by analysis of historic data, the prediction engine sales can be obtained. Forecasting methods and their selection, however, have much effect on the result of prediction. Comparison and analysis of different predicting methods and their errors are discussed. The application of forecasting methods to foreseeing sales is explained based on the data of an engine manufacturer.
Key words:engine, market demand, fluctuation sale, prediction
作者简介:徐炜(1970-),男,在读工程硕士,主要研究方向为工业工程。
doi:10.3969/j.issn.1671-0614.2015.02.011

