工科数学——祖冲之思路

钟万勰

大连理工大学

工科数学
——祖冲之思路

钟万勰

大连理工大学

前 言

中国的大学工科数学教材，讲的全部是国外数学家成就，“言必称希腊”。作者常常怀疑，难道历古以来光辉灿烂的中国文化，竟然在数学方面一无所成？然而，我们是在工程力学方面做研究与应用的，毕竟是数学外行。教育部邀请许多数学家所编写的教材写成为：全部由洋人所贡献，也是无可如何。有疑问：中国工科数学教材，难道中国人的贡献竟可被不屑一顾地完全忽略，连立锥之地也不容吗？

对此难以认同，不平则鸣么！作者不是数学家，难免有所舛误，有错就请批评，不用客气。

作者这些年在动力学方面努力，尤其是有约束的动力学计算分析，发现作为机器人动力学基础的约束动力系统微分-代数方程(DAE, Differential-Algebraic Equation)的求解，例如现代著名著作

E.Hairer G.Wanner:Solving ordinary differential equations II-stiff and differential-algebraic problems 2nd ed.ch.7.[M],Springer,Berlin,1996. E.Hairer,Ch.Lubich and G.Wanner:Geometric-Preserving Algorithms for Ordinary Differential Equations.Springer,2006.

大力论述DAE的求解，效果不理想。一些著名洋人软件，例如广泛应用的ADAMS，其数值结果也不理想。因为这些著作的求解方法，是先进行微商，将约束方程归化到微分方程，其微商次数称为Index，可称为Index法。看起来约束条件处处满足，而实际上数值结果的约束条件满足不行。按“实践是检验真理的唯一标准”，不行。

钟万勰，中国科学院院士，大连理工大学工程力学研究所所长、教授。工程力学、计算力学专家。1956年同济大学桥梁与隧道系毕业。1993年当选为中国科学院院士。

上世纪60年代发现潜艇耐压锥、柱结合壳失稳的不利构造形式。70年代与小组基于群论研制了大量工程应用软件，并主持研制了三维大型有限元系统JIGFEX／DDJ。80年代提出了基于序列二次规划的结构优化算法及DDDU程序系统提出结构极限分析新的上、下限定理，继而又提出了参变量变分原理及相应的参变量二次规划算法用于弹－塑性变形及接触问题，是中国计算力学发展的奠基人之一。1989年以来，发现了结构力学与最优控制相模拟据此又提出了弹性力学求解新体系与精细积分的方法论。

中国著名南北朝数学家祖冲之(429～500)在计算圆周率π时，已经达到π＝3.1415926～3.1415927之间，唐朝魏征等撰写的史书《隋书》中有记载∶

（古之九数，圆周率三，圆径率一，其术疏舛。自刘歆、张衡、刘徽、王蕃、皮延宗之徒，各设新率，未臻折衷。宋末，南徐州从事史祖冲之，更开密法，以圆径一亿为一丈，圆周盈数三丈一尺四寸一分五厘九毫二秒七忽，朒数三丈一尺四寸一分五厘九毫二秒六忽，正数在盈朒二限之间。密率，圆径一百一十三，圆周三百五十五。约率，圆径七，周二十二。又设开差冪，开差立，兼以正圆参之。指要精密，算氏之最者也。所著之书，名为《缀术》，学官莫能究其深奥，是故废而不理。）

学官厉害，我不懂就废而不理。当然这是古代官僚机制。找官告状，就得先跪下。古代数学受到严重打击。祖冲之的《缀术》为之失传；然而今天毕竟还有刘徽（三国魏人）的《九章算术》传世。今天我们应将祖冲之算法挖掘出来，“继绝世”，融合现代数学，解决今天的问题，发扬光大。贯通古今，融合中西。

如所周知，π是现代数学不可回避的基础，看到中国祖师爷的重要贡献，欣喜不已。于是我们就探讨祖师爷祖冲之在当年条件下是怎么计算的。由此引申下去，其实许多数学基本概念，例如无穷序列，极限等等，中国祖师爷也是明白的。并且在实际上应用了，按此路线探究下去就接地气。尤其是接中国人的地气。

所以，中国数学并非一无所成，而是挖掘不够。窃以为，既然在中国大学讲数学，就不应将中国数学祖师爷的工作忽略，而应有所传承。我们不可“光说不练”，本文就从祖冲之如何计算圆周率π讲起，加以传承，贯通古今，融合中西。中国数学也应占有一席之地的。可先从中国工科数学教学做起。

2014年5月，钟万勰参加了在广东工学院的工科数学教材会议，介绍了祖冲之类算法。希冀大学数学教材要加入中国元素。本文是以实际工作贯彻该意图。不仅是讲讲而已，而要有实际行动的。期待官方能任领导改革之职。下面就由探讨祖冲之的工作开始。

著作[10]的序言中讲：“1999年5月，教育部委托上海大学在钱伟长教授主持下召开了一次应用力学教改的会议。该会议使我下决心写出这本书，为此花费了大量的精力。”表明钟万勰很早就有志于教学。虽然曾努力推动，但思路不得法，效果不理想。现在再一次努力，希望能发挥应有作用。但钟万勰困惑：教育改革没有SCI，得不到评价，又怎能鼓励青年教师呢。官僚机制厉害呀！当官只要数数SCI就可以了，懒政！此“官不任事”者也。面对这种评价机制，只能长叹：“此天之亡我，非战之罪也！”，对此唏嘘不已。

一，祖冲之是如何计算圆周率π的估计

中国人古代早就关注圆周率了，所谓“周三径一”，那只是一个约略的估计。设平面上有一个直径为2的圆，半径r＝1，要计算圆周长度，当然是2π了。但当年祖冲之又是如何计算的呢？

中国在东周时期，已经发明了算盘，并且申了遗。算盘是古代的计算机。并且中国勾、股、弦的定理也早已发现，周公时期(公元前1000多年)已经有所记载，称商高定理。古代希腊有毕达哥拉斯者，对此有系统论述，所以大家说这是毕达哥拉斯定理。我们可仍称呼为商高定理。因为祖冲之未必知道有毕达哥拉斯者，他实际可使用中国传承下来的商高定理。

平面上两点之间的最短距离是其连接直线的长度，今天说法是平面欧几里得几何的短程线。这些基本概念是祖冲之算法的基础。

一个圆有内接正多角形，有如切西瓜(古代称为割圆术)，1分为2,2分为4,4分为8,…。每次划分全部是n=2i，i＝0,1,2,3,4,…。圆周生成了n条边的内接正多角形。当切了i=2次，就有内接4边形，总是半径r=1，此时每块等腰三角形的张角是90o。切下的内接正多角形圆弧，不计算圆弧长度而用短程线的长度替代，成为等腰三角形。i=2时两点连直线的长度是l2=。等腰三角形有中垂线将三角形划分为2个直角三角形。其勾的长度是a=l2/2，弦的长度就是r=1。中垂线的长度（股b）可根据商高定理a2+b2=r2=1而计算。股的长度b当然小于半径r=1。于是得到1-b，这是将中垂线延伸到圆周点p的长度，见图1。

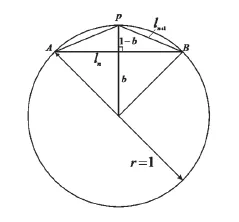
图1.割圆术

以延伸长度1-b为勾，以前面的a=l2/2为股，再根据商高定理可计算其弦，就是n=2i+1正内接多边形的边长li=3。于是计算圆周长度2π的近似，内接正多角形边的总长是2ixl。i

图1为半径为r=1的圆，计算圆周率，采用割圆术计算，用内接正多边形的总周长近似为圆的周长。实际计算的可以是半个圆周。假设正n边形的总边长为li，n=2i，用li作为弧长的近似。按上文所述，勾a=li/2，弦为1，而按商高定理得b=[1-(li/2)2]1/2的股。

再用商高定理。以伸长线1-b为勾

1-b=1-[1-(li/2)2]1/2=1-[4-li2]1/2/2=[2-(4-li2)1/2]2，以a=li/2为股，则给出2li+1=2×[(1-b)2+(li/2)2]1/2=[4(1-b)2+li2]1/2。将4(1-b)2=[2-(4-li2)1/2]2=8-4(4-li2)1/2-li2，代入有

这样，就形成了一次等腰三角形的分割，式(1.1)形成了递推回归形式。无非是将2条边的长度si+1=2li+1相加在一起而已。

具体计算可从半个圆开始，取为i=1,s1=l1=2。即计算半个圆周的弧长，半径1，张开角是1800。结果弧长应该是π，而与i＝1，s=l1＝2相差很多。再分解一次则有l2，而张开角成为900的2段圆弧，近似为2个三角形其边长之和是s2=2l2=2=2.8284；与π逼近了些但相差依然很大。再继续划分2个等腰三角形，900的一段圆弧，成为张开角各为450的2段圆弧，近似长度s3=2l3=22l2；如此继续下去…。从li计算li+1的公式是(1.1)。其数值结果罗列于表1之中。

内接正多角形的总边长，永远赶不上2π，因为连接线是直线短程线；然而可不断逼近2π，得到序列。所以，得到的无穷序列是无限逼近于2π的，2π就是其极限。具体数值计算给出

表1：不同正多边形对应的圆周率

表1为用SiPESC集成平台调用的Python编程计算得到的表格，可见当取正16384边形时，近似计算得到圆周率为.14159263，此过程不断进行，得到了无穷序列，其极限就是圆周率π。

所以说，祖冲之肯定有无穷序列和极限的概念。通过割圆术这样的具体问题来讲述无穷序列和极限，接地气，容易理解。教学么，本来应当如此。

中国大学工科数学教材可在祖冲之的基础上讲授下去。中国特色、中国元素么。直观，而又接地气，毕竟工科与理科纯数学的要求不同。形成切合中国自己的那一套，让学生容易懂，那才是今天应关注的。

科学网2015-5-24传达韩启德说：“中国科学家缺位科普”。在工科数学中，中国数学家也是缺位的。让我们来改变这个不合理的现状吧。

感慨：人云：“如欲亡其国，应先灭其史”！灭其史干什么，为了丧其志！连爸、妈是谁都不知道了，丧了志，浑浑噩噩，任人摆布，那就什么也没有了。警惕呀。

中国数学如自动缺位，前途堪忧。

应从基本概念方面提炼出祖冲之算法的特点：圆弧全部用短程线的直线代替。除节点外，短程线的点全部不在圆周上。将圆周看成约束，则除节点外，只要短程线的要求得到满足，不必再考虑其约束。这是在二维欧几里得几何条件下得到的。我们当然希望将祖冲之思路推广到更广泛领域中去。事实上这是成功的。在动力学DAE的推广，比国外许多著作用的Index法好多了。见后文。

虽然祖冲之当年未必知道有短程线之说，但直观上一定知道直线是最短距离。直观没有什么不好，不要苛求。冯·诺伊曼的文章《数学家》[1]应该读一读，不要追求绝对的严格性。

数学大师冯・诺伊曼指出：“能以更好的形式推广为更有效的新理论的理论将战胜另一理论。…必须强调的是，这并不是一个接受正确理论、抛弃错误理论的问题。而是一个是否接受为了正确的推广而表现出更大的形式适应性的问题”，见文献[1]。

上文推测了祖冲之计算圆周率的方法。如仅仅只是用在二维欧几里得空间，那未免太局限了。祖冲之算法的思路非常宝贵，应寻求将其使用于广大领域。有中国特色成果，应予以收复失地。

对于中国大学工科数学教育来说，本文不免有些“说三道四”。但我在大学工科工作了一辈子，难道连这些话也不该说吗！

党中央推动改革。官员有公权力，希望能有担当，领导我们改掉不合理的教材吧。希望有关部门能予以关注，改革3的路就在脚下，难道工科数学就不用“认祖归宗”吗？ 振作起来干吧！

二，无约束动力学的时间积分

牛顿的奇迹年是1665～1666，后来1687年牛顿出版了巨著《自然哲学的数学原理》是用希腊文写就的，简称principia，是近代科学开始的标记，同时也创立了微积分，这是划时代的成就。书名表明是自然哲学，经典动力学的数学理论由此开始。牛顿主要考虑天体力学方面的问题。随后分析动力学则得到当年众多大数学家的关注，Bernoulli,Eule r,Lagrange,Hamilton,Jacobi,Poisson,Poincare, …，经典动力学就是他们奠基奉献的。Euler-Lagrange方程，Lagrange函数，Hamilton变分原理，正则方程，Hamilton-Jacobi偏微分方程，正则变换，作用量，摄动法，…，成为优美的数学分析体系。牛顿提出微分方程求解的方法；Euler-Lagrange提出能量方法，Hamilton则提出了正则方程，其自变量扩展到了2n，其中n是位移自由度数。位移法的Euler-Lagrange方程，是n个二阶微分方程；而Hamilton正则方程则是状态空间的2n个一阶对偶微分方程。

经典力学众多著作是许多著名数学家努力耕耘的成果。内容丰富、数学理论优美，难以穷尽。这里不过是取其中心部分内容讲解，毕竟是教数学么。然而对于Hamilton体系的认识，却有曲折过程。

冯康说[4]：从历史上考察人们对Hamilton体系的评价，Hamilton本人是从几何光学着手创建他的理论模式的。1834年Hamilton曾说：“这套思想与方法业已应用到光学与力学，看来还有其他方面的应用，通过数学家的努力还将发展成为一门独立的学问”，这仅仅是他的期望。19世纪同时代人对其反应则很冷淡，认为这套理论“漂亮而无用”。著名数学家F.Klein(International Congress of Mathematicians,ICM，1897年第一届苏黎士大会主席)在对Hamilton体系的理论给予高度评价的同时，对其实用价值亦持怀疑态度，他说“这套理论对于物理学家是难望有用的，而对工程师则根本无用”。这种怀疑，至少就物理学的范畴而言，是被随后的历史所完全否定了。到了20世纪量子力学的创始人之一Schroedinger曾说：“Hamilton原理已经成为现代物理的基石…，如果您要用现代理论解决任何物理问题，首先得把它表示为Hamilton形式”。说明了Hamilton状态空间法的重要性。

量子力学当年面临的一个关键问题是光谱分析。观察到的谱线分裂现象，被Hilbert的大弟子，大数学家Hermann Weyl用群论分析清楚[2]。进入Hamilton状态空间后，H.Weyl在1939年又提出Symplectic对称[3]。华罗庚先生音译为‘辛’。H.Weyl提出了Hamilton正则方程的辛对称，表明了动力系统运行的基本性质，表征了动力学的辛阶段。

辛，是大数学家Hermann Weyl在名著[3]中提出的。作者写道：“The name ‘complex group’ formerly advocated by me in allusion to line complexes, …has become more and more embarrassing through collision with the word ‘complex’ in the connotation of complex number.I therefore propose to replace it by the Greek adjective ‘symplectic’ ”

表达了为避免“complex”容易产生的混淆，特地引入的希腊形容词‘symplectic’。

H.Weyl的工作吸引了纯数学家们高度关注。从微分几何的角度出发，给出了“辛几何”的定义；但其理论过分高深以致让工程师难以接受。今天已经是信息时代，计算机的发展使人们认识到“计算科学”的重要性。“计算科学与理论、实验共同构成现代科学的3大支柱”的论点得到了广泛认同。计算科学是当代数学的大发展。计算科学的主要特点是离散。计算机本身就是离散的么。

“世界潮流，浩浩汤汤，顺之者昌，逆之者亡。”

辛几何：数学家从纯数学微分几何出发，定义：微分形式，切丛、余切丛(tangent,cotangent bundle)，交叉外乘积(exterior product)，Cartan几何等。艰涩难懂。离散后就成为：

辛代数：容易理解、掌握。回归到力学，离散系统。可从虎克定律讲清楚，见[9]。自然科学基金1993年支持了课题(19372011)“结构动力学及其辛代数方法”。辛代数的提法不是现在才有的。

我国数学家冯康率先提出[4]，动力学积分的差分格式应保辛，差分格式就是离散积分。国外著作[5]也接受了。

祖冲之算法首先是用于离散系统的，切实符合计算科学的需要，所以前程远大。自然可用于离散后的动力学方程。牛顿是动力学和微积分的祖师爷(德国的Leibnitz同年代也从几何方面提出了微积分)；同年代的虎克(Robert Hooke)是结构力学的祖师爷，弹性力学不能回避虎克定律。然而当年两人不和[6]，因此分道扬镳，各自独立发展。Hamilton状态空间方法未能进入弹性力学领域，直至著作[7～8]的出版，才改变了求解思路。

作者随后在著作[9～12]，建立了分析动力学与分析结构力学的模拟理论。会同以前建立的计算结构力学与最优控制间的模拟理论[13,14]，将多个领域皆奠基于状态空间的数学理论。于是各个领域的数学计算方法可以互通有无了。基础就是状态空间法的辛对称。

1900年在第二次世界数学大会上，D.Hilbert做了一个著名报告《数学问题》，深刻影响了20世纪数学的发展，指出：“只要一门科学分支能提出大量的问题，它就充满着生命力；而问题缺乏则预示着这门学科独立发展的衰亡或终止。”能看到问题就好，表明可继续发展。辛指出Hamilton正则方程有对称性，是经典力学继续发展的机会，有大量的新问题。《数学问题》中提出23个问题，其中第23号是变分法的进一步发展。Hilbert说：“我已经广泛地涉及了尽可能是确定的和特殊的问题…，用一个一般的问题来做结束…我指的是变分法”，见文献[15]。变分法不单纯是一个数学问题，而是一个方向，是大师的远见卓识。

变分原理的提出，由来已久。“大自然总是走最容易和最可能的途径”，这是费尔马(Fermat)著名的自然哲学原理。1744年，J.Bernoulli提出了“最速下降线”问题，大体上可认为是数学变分法的开始。以后蓬勃发展，Euler-Lagrange方程，继而总结为Hamilton变分原理。分析动力学与相应的常微分方程理论的成功，自然要发展到偏微分方程。到位势理论，有Laplace方程的求解，Green,Gauss,Dirichlet等先后指出，可将其转化为变分原理。Riemann(1826～1866)将其命名为Dirichlet原理，属于椭圆型偏微分方程理论，本来在蓬勃发展。然而在1870年发生了曲折，强调数学严格性的维尔斯特拉斯(Weierstrass)否定了Dirichlet原理；然而数学物理中许多重要结果都依赖于此原理而建立。1899年,Hilbert用边界条件的光滑化保证了极小化函数的存在，从而挽救了Dirichlet原理。表明变分原理经历了“凤凰涅槃，浴火重生”的过程。

此后一个多世纪以来，变分原理有了巨大进展，从有限元法发展出来的“计算科学”也是变分法的发展；而辛也属于变分法的发展。我国在变分原理的研究方面是有成就的，胡海昌的三类变量变分原理蜚声世界。有限元法离散取得了巨大成功，有限元单元推导的基础就是变分原理。动力学变分原理称为最小作用量原理。做一点解释如下。

设物体有n个自由度。Lagrange函数L(q, )=T-U是动能T减势能U，是n维位移q(t)和速度(t)向量的纯量函数。在数值求解之前，介绍一下国外发展的许多方法是有益的。

随着计算力学、有限元，以及航空航天等的推进，动力系统的求解成为不可缺少。绝大部分课题分析求解无望，只能数值求解。国外数学家大力发展Runge-Kutta，Newmark法等许多差分算法，可谓五花八门；继而国外进行了许多研究，一批保辛差分算法相继出现[5]。动力学系统的积分特别讲究所谓首次积分(fi rst integral)，其实就是积分不变量。其中能量守恒特别重要。

然而，继续的研究却走入了歧途。1988年，[17]提出了“保辛则能量不能守恒”的误判。文献[18]用参变量达成了离散近似系统在保辛的同时依然保守的算法，并在著作[19]中给出了系统的论述。表明计算科学的发展，催生了辛对称的深入发展，并且还应当突破矩阵群论的等维数限制，还有时间滞后等问题，前途广阔。著作[19]只是初步试探而已。

既然分析求解困难，则只能离散数值求解，差分法是常用的。我国数学家冯康提出，差分格式应保辛，棋高一着。设时间划分为步长η的一系列节点 to=0,…,tk=kη,…。逐步积分要在积分出tk-1的状态后，进一步积分时间区段k#:[tk-1,tk]，以计算tk的状态。此时可用最小作用量原理。时间区段k#:[tk-1,tk]的作用量是

作用量可从例如[16]找到。动力系统通常是没有约束条件的。

采用时间有限元法[21]积分。时间tk-1的状态qk-1,pk-1已经计算出来，以下要求解时间tk的状态qk,pk。在k#:[tk-1,tk]内位移用两端位移向量qk-1,qk插值，例如简单些线性插值。时间有限元法完成积分得到有限元近似的作用量

然后，按一般理论，有

其中qk-1,pk-1为已知。至于子矩阵Kaa,k就简单地写成Kaa了。于是

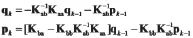
该表达式的右侧全部是已知的qk-1,pk-1，用状态向量表达则是vk-1；而右侧是待求的qk,pk，用状态向量表达则是vk。组成传递矩阵

其中子矩阵Kaa,k简单地写成Kaa了，等。其实这就是按[9]所述，2nx2n对称矩阵Kk变换到传递辛矩阵Sk的公式，数值积分可按此进行。的公式可自行验证。然而，此种传递辛矩阵的积分，却不能保证每步的能量保守。如果要能量保守，则还应按文献[23]加参变量的处理。

一般的动力学积分是没有约束的，相对比较简单些。而祖冲之类算法并不要求区段k#:[tk-1,tk]内满足约束，而只要求在离散时间点处满足约束条件。

虽然依然有许多问题，例如刚性(stiff)等不同尺度的问题。但毕竟没有约束，相对比较好对付些。如果还有约束条件，同时要进行时间积分，就会出现微分-代数方程了。求解DAE是机器人动力学必要的基础，祖冲之类算法可以发挥基本作用，下一节会讲的。首先要积分无约束的动力学问题。

这方面有许多数值例题，不再重复。本节是初步的分析动力学的内容，时间有限元么。对于祖冲之类算法，不管约束条件而取“动力学意义下的短程线”来说，是不可缺少的基础。有了基础，就可讲动力学的祖冲之类算法了。

三，祖冲之类算法

现代化推进使机器人成为发展的热点。机器人要运动，当然需要动力学分析。机器人起码是机构，机械工程离不开机构。机器各个部件皆可运动，但相互间是有位移几何约束的，称为完整约束。因此我们面临受约束的动力学系统分析问题。国外发展了称为微分-代数方程(DAE,Differential-Algebraic Equation)的求解方法。DAE的求解成为一个重要问题，祖冲之算法可推广用于此类重要问题。著作[20]的副标题就直接写上了stiff and differential-algebraic problems。论述了DAE的求解，但效果不理想。因为这些著作的求解方法，是先进行微商，将约束方程归化到微分方程，其微商次数称为Index，可称为Index法。看起来约束条件处处满足，而实际上数值结果的约束条件满足不行。

上节，介绍了的是传统的分析力学，无约束。哈密顿体系理论是很一般的，并不限于线性体系，而是对于保守体系的[16]。动力系统的数值积分吸引了众多研究，有代表性的著作见[20,5]。许多实际课题引导到有约束的Hamilton系统(Constrained Hamiltonian system)，总是推导到微分-代数方程(DAE)。国外通常求解方法采用对于代数约束进行微商，Index法，并归化到联立常微分方程组再进行数值求解的方法。但数学理论方便，并不代表数值方法有效。从数值求解的角度看，反而使问题变复杂了。

代数方程本来就是微分方程组的积分，反而将它化成微分方程再进行数值积分，多余的“虚功”么，坐回头车了。归化到微分方程组再进行离散数值积分，前面的归化步是连续的精确的，而离散数值积分是近似的，往返不等价么。方法论已经不合适了，怎么可能比原来的代数方程约束更精确、更方便呢。走偏路了！

采用祖冲之类算法的思路，时间积分的格点处，要求位移约束严格满足；而在时间区段内则不管位移约束了，要求“动力学意义下的短程线”即可。现在是动力学，要求的短程线应是2n维状态空间的短程线，因为在时间积分的区段内不管位移约束条件了。

格点处的位移代数方程显然比微分方程容易数值处理，可在数值求解时作为等式约束同时迭代满足。等式约束比不等式约束的处理容易多了。求解DAE的这方面可见文[24]，从其中的简单例题，可看到约束条件的满足是非常好的，表明index积分方法不可取。虽然这是国外众多著作采用的，但数值例题表明不够理想。

完整约束是直接对位移的，在每个时间节点可以方便地表达而不涉及位移的时间微分或动量的。容易在每个节点单独处理的。理论上讲，约束条件是完全在位移空间(Configuration)的。节点位移满足约束条件，意味着位移和动量都只有n-nc个独立分量，其中n,nc分别是位移和约束的维数。代数约束方程(位移空间的约束)不包含动量，故离散后的约束只与本节点的位移有关，而与相邻节点无关。节点k的相邻时间区段是k#:(k-1,k)以及(k+1)#:(k,k+1)。k#区段积分时得到的，受到的约束与(k+1)#区段的k点同，因为总是与k点的位移约束方程的切面相垂直(理想约束)。因此可直接用于。即动量在节点处是连续的。这给DAE的祖冲之类算法求解带来了方便。

设q(t)是n维广义位移向量，无约束时动力系统的Lagrange函数为，T,U分别为动能，势能。但当运动时有nc维的理想约束，约束方程为

运动只能在约束下的超曲面(流形,Manifold)上运动，即q(t)已不是独立的广义位移。其动力方程的推导是引入nc维的Lagrange乘子函数λ(t)，组成扩展的Lagrange函数

导出的方程组是

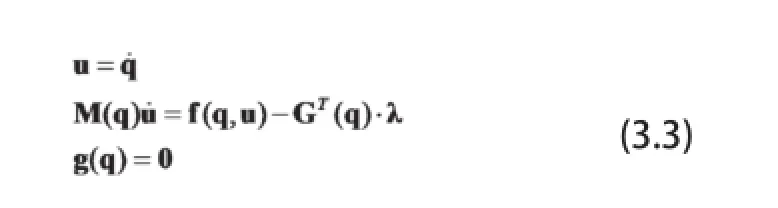
对应的DAE为(这些是国外的方法论)

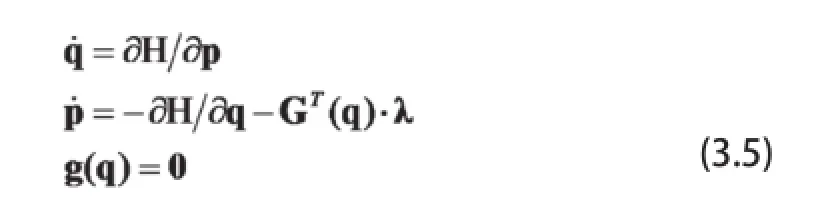
H(q,p)=E是保守的。此即在状态空间q,p下的微分-代数方程[5,20]。国外求解方法论的基础是微分方程，要推出联立微分方程引起指标(Index)问题等，给理论与计算上带来了复杂的附加因素。

微分—代数DAE方程的求解有广泛应用，但非线性系统的DAE方程并不是可轻易地求解的，多种常见的差分近似已经有了较深入的探讨。但差分的插值本来不满足约束条件的。反而难以保证轨道在格点处满足位移约束条件。只能在每步积分后再采用投影等修补手段，这种修补成了一种干扰。因其方法论是先用差分法离散约束产生的微分方程，然后再考虑约束。差分近似本身的精度就不够，哪怕注意到了差分近似的保辛，但其投影修补是否保辛也是问题。随着该思路有许多研究，但方法论不行。走偏路了。

“行成于思，毁于随”。既然现有求解方法论不理想，就应重新探讨。孙子兵法曰：“出其所不趋，趋其所不意”，本文要改变其求解方法论。其实中国数学祖师爷早已有世界首创的工作了。这就是引申为祖冲之类的算法。看看我们中国人是怎么求解的。

在计算圆周率π时，祖冲之给出的思路是，约束条件不必处处满足，只要在节点处严格满足就可以了，而相邻节点间则可用短程线代替，而不用管nc维的约束条件。

同样的思路也可运用于DAE的方程求解。先进行离散，约束条件只要求在节点处严格满足，而轨道则可按无约束动力系统积分，(动力学意义下的短程线)，例如可用时间有限元近似积分。只要节点划分足够密，则轨道定会逼近真实解的。这样的思路下导出的算法，可称之为祖冲之方法论、祖冲之类算法。我们理应接住1500多年前祖师爷传来的球，挖掘继承，发扬光大，与近代数学融合。“古为今用，洋为中用”，向前冲之。

回顾Lagrange力学的基本思想，是先引入广义位移以满足全部约束条件的，但祖冲之类算法改变了其思路。Lagrange体系要处处满足约束条件的广义位移难以找到，但本文运用分析结构力学的基本概念，进入离散系统来分析。首先保证离散积分点的nc维约束条件严格满足；再在时间区段内，用时间有限元[23]离散代替差分离散，然后运用作用量的变分原理以代替微分方程，离散的时间步内就不再考虑约束了，因插值函数本来不能满足。离散在先，分析结构力学理论保证可达到每步积分的自动保辛，继承了祖冲之方法论的思路，称祖冲之类算法，特色思路么。祖冲之的古代，没有微积分、动力学等，但其思路可以继承(贯通古今)。融合近代科学理论(融合中西)，得到的算法可称之为祖冲之类的算法。中国在现代数学发展中，不可缺位。祖冲之类算法，可提供一个例证。

基于分析结构力学理论的方法，可从最简单的例题着手阐明。

例题1：质量m的单摆振动，取q(t)={x,y}T为未知数，而不用θ(t)。约束条件g(q)r2-(x2+y2)=0,r=1。初始条件x(0)=0.99,。

解：y坐标以向下为正，势能U(x,y)=-mgry, gr=10m/sec2；动能，Lagrange函数，其变分原理

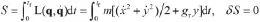
其中gr是重力加速度。

首先将时间划分为步η的一系列节点to=0,…,tk=kη。按祖冲之方法论，只考虑时间格点处的约束条件，是离散的。对应地，其nc维约束的Lagrange参数向量λ也是离散的，不再有对nc维向量λ微商之说。对应于离散格点有λk,k=1,2,…的nc维向量待求。

扩展Lagrange函数的作用量，也要相应地离散。区段k#:(tk-1,tk)内按祖冲之思路，不用考虑约束，因此位移仍是n维。但到k号时间节点tk时，要将nc维向量λk考虑进去。

分别对区段位移分量进行简单的线性插值，单元内部的约束条件则放松掉。运用有限元法近似计算作用量。线性插值有。但还要加入时间节点tk处的约束对偶向量λk，于是与完全无约束的(2.2)对比，应修改为

它相当于结构力学的区段变形能。整体变形能无非是全部单元变形能之和

由于插值公式，相当于作用量(区段变形能)用的有限元近似与真实作用量略有不同。Lagrange原理的位移约束条件已经在节点处严格满足，区段内部的约束条件则由有限元插值自然就近似满足了。其逐步积分求解是积分区段k#:(tk-1,tk)时，将qk,λk同时求解，然后再积分下一个时间步。

将节点约束条件(1.1)推迟到数值积分时一起处理。利用节点的nc维Lagrange参变向量λk。参变量λk则用于处理tk处的约束条件。单元内位移则用有限元插值

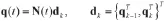
积分就得区段作用量sk(qk-1,qk,λk)。因未曾满足节点约束条件，故位移qk仍是原来n维的，不是约束后的独立位移。该作用量对参变量λk是线性的，可表达为

根据

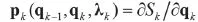
与无约束系统相比，多了线性参变量 。组成各站的2n维状态向量

按分析结构力学方法进行，从vk-i可递推vk，该变换保辛，但带有参变量λk。确定λk要根据节点约束条件g(qk)=0。

建议运用线性的有限元插值函数 N(t)，因区段内的约束条件并未严格满足，用线性函数插值近似来满足，可能效果好些。

本方法用参变量线性λk满足节点约束条件g(qk)=0。未知数包含线性参变量λk与全部节点状态vk，有2n+nc个未知数要求解，仍是非线性联立代数方程，保辛。能提供的方程是带有参变量λk的传递矩阵2n个方程，以及节点位移约束条件g(qk)=0，也是共2n+nc个非线性方程。

可归纳分析结构力学(带参变量λk)的算法如下：

1)形成Lagrange函数(动能—势能)，并引入约束的Lagrange参数，形成扩展Lagrange函数。

2)将时间坐标离散，得一系列的时间点to=0,t1,…,tk…，以各点的n维位移qk当作未知数。

3)按分析结构力学，计算区段(tk-1,tk)的作用量sk(qk-1,qk,λk)，可用有限元线性插值得作用量。

4)生成对偶向量

组成状态向量。

5)根据

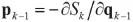
以及初始条件，对1号单元，用插值公式计算初始p0并组成初始状态。

6)各单元的辛矩阵可从方程

会同约束条件g(qk)=0解出。成为根据qk-1,pk-1计qk,pk,λk，完成逐步积分的保辛递推。

分析结构力学的算法运用时间有限元，不具体考虑约束对偶λ的微分方程，而是将λk逐点当作待定的常参数。因不涉及其微商，故不必考虑其微分方程，也不会产生DAE微分方程理论的Index问题。通过数值例题可看到祖冲之方法论，祖冲之类算法特色思路的效果。本课题的数值结果展示了优越性。

可提供更多的数值例题以供比较。本文展示约束保守体系的分析结构力学DAE有限元保辛算法的解。

例题2：选择3维球面摆[5]p.210的例题。

解：按[5]取重力加速度取gr=1，摆的长度为1，质点质量为1，z坐标以向下为正。Hamilton函数为

初始位置为

初始动量为

积分步长分别取为0.03秒和0.1秒。图2给出了球面摆质点的轨迹图。因满足约束条件是本算法的基本点，故不再展示约束。图3给出了系统的Hamilton函数随时间变化情况。文献[5]213页分别用辛欧拉算法和投影辛欧拉算法，给出了同样问题的Hamilton函数和质点偏离约束面的情况，可以看到两种算法的Hamilton函数都随时间线性增长，保辛效果不理想。将本文的图3与它们比较，可以看到本文算法的保辛效果好，对约束的满足具有非常高的精度，具有更大的优势。

例题3：空间双摆问题：质点1的初始位置是

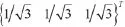
初始速度是{0.1 0 0}T，质点2的初始位置是

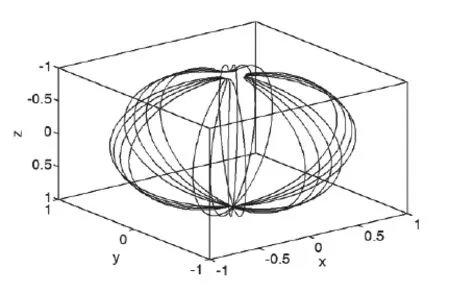
图2.球面摆质点的轨迹图(步长分别为0.03秒和0.1秒)

图3，球面摆Hamilton函数随时间变化，真实H=0.99680

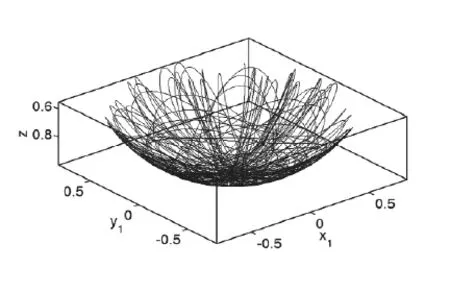
图4.质点1的轨迹，约束条件满足非常好

初始速度是{0.2 0 0}T，积分步长为0.01秒。积分结果如以下。图4是质点1的轨迹图，图5是质点2相对于质点1的轨迹，图6是质点2的绝对轨迹。图7是系统的Hamilton函数随时间变化情况，可以看到Hamilton函数在两个确定数值之间震荡，不会线性地偏离，并且这两个数值和系统真实的Hamilton函数相差很小，这说明保辛效果很好。

通过这些数值例题，读者可看到如何计算求解，并看到其效果。这些数值结果，其位移曲线出现混沌现象。这是非线性系统的特性。该满足的约束条件，满足得非常好；等步长积分，能量Hamilton函数，虽然有所偏离但也满足得很好了。比国外著名算法好多了。

DAE不但在非线性动力学求解中非常有用，(以上讲的例题全部是经典动力学的)；而且在电网的网络控制问题等课题中也很有用。虽然问题早就存在，好在DAE求解数值问题得到关注的时间还不是很长。以上提出的迭代法逐步积分，与洋人的Index方法完全不同，其效果从这些简单例题中已经表达。用事实说话。

我们学习了许多著名数学家的名言，有些体会。教材就应当易学易懂，不怕人家说土，说水平不高。我们就是土生土长的么。Hilbert在《数学问题》中说：“清楚的、易于理解的问题吸引着人们的兴趣，而复杂的问题却使我们望而却步”，又说：“在讨论数学问题时，我们相信特殊化比一般化起着更为重要的作用。可能在大多数场合，我们寻找一个问题的答案而未能成功的原因，是在于这样的事实，即有一些比手头的问题更简单、更容易的问题没有完全解决或是完全没有解决。这时，一切都有赖于找出这些比较容易的问题并使用尽可能完善的方法和能够推广的概念来解决它们。这种方法是克服数学困难的最重要的杠杆之一。”

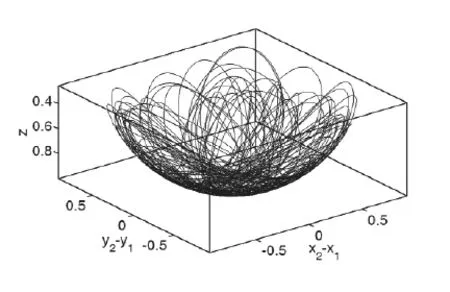
图5.质点2相对于质点1的轨迹，约束条件满足依然非常好

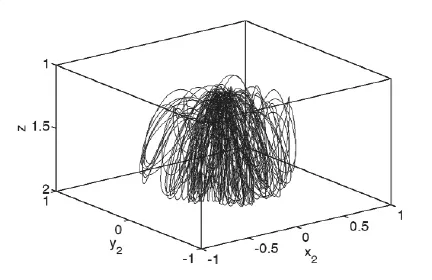
图6.质点2的轨迹，混沌出现了

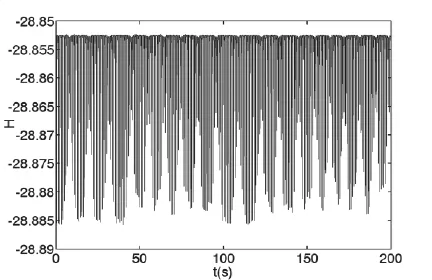
图7.Hamilton函数随时间变化，真实H=28.85251

D. Hilbert《数学问题》：“数学中每一步真正的进展，都与更有力的工具和更简单的方法的发现密切联系着，这些工具和方法同时会有助于理解已有的理论并把陈旧的、复杂的东西抛到一边。数学科学发展的这种特点是根深蒂固的。因此，对于个别的数学工作者来说，只要掌握了这些有力的工具和简单的方法，他就有可能在数学的各个分支中比其他科学更容易地找到前进的道路”。

本文涉及了辛矩阵对称群，读者可能对群论有些怕。其实本文只用到群的最简单原理。英国M.Atiyah(1990年当选的皇家学会会长，著名纯数学家)说[26]：“群在自然中产生，它们是使事物运动的东西，它们是变换或置换…。理解这些东西的本性，并且使用它们才是目的”。又说：“重要的东西常常不是技术上最困难的即最难证明的东西，而常常是较为初等的部分。因为这些部分与其它领域、分支的相互作用最广泛，即影响面最大”。“在群论中有许多极端重要的，并且在数学的各个角落到处都出现的东西。这些是较为初等的东西：群及其同态、表示的基本观点，一般的性质，一般的方法—这些才是真正重要的”。作者也由此得益，这些观点对读者也许有益。

作为机器人基础的DAE，基于祖冲之方法论得到的解，比国外著名算法的解好多了。中国祖师爷的优秀成果应努力予以挖掘继承，融合近代数学，发扬光大。中华文化博大精深，不只是怀念怀念，而应以实实在在的东西体现出来。当然还应经历挖掘、品味、提炼、继承、融合近代数学、然后才能发扬光大。学习大学微积分，读完后没见到中国人实实在在的贡献，遗憾；到现在信息时代，挖掘出祖冲之方法论，理应占有一席之地。我们应为此而站起来大喊大叫。“南海诸岛一千多年前就在中国的管辖之下”，我们应理直气壮地讲，因为有事实依据。有人不承认，难道我们就不敢讲了吗！今天看到祖冲之方法论的优越性，可达到贯通古今，融合中西的境界。中国人就应占有这一席之地，有什么不敢讲的。难道这也要等着，让洋人来发扬光大吗?! 他们会吗？

当前中国一些人治学，重洋轻华，“言必称希腊”。保辛离散体系，是新事物，洋人也措手不及，例如他们提出“不可积系统，保辛近似算法不能使能量守恒”的误判，我们也予以了正名，中国人切不可自卑。所谓的SCI评价体系，同样的论文，英文发表就比中文发表值钱，真荒唐！民族虚无主义，可耻！

对自己没有信心，弱者的心态么，要不得。

当年红军英勇奋斗，请了李德，就打败仗。道路决定命运么。评价体系是学术研究的指挥棒。提出一个什么SCI等的洋指标，完全放弃了自主，又请来了一个“李德”，特别不爽。

中国数学界泰斗、中科院院士吴文俊认为：“数学应该是有助于解决实际问题的，这应该是研究数学的主要目的，数学不是什么抽象的理论。…中国的应用数学应该以解决实际问题为出发点的，绝不能只做抽象的理论研究。”

改革！你讲你的，我讲我的。力求返璞归真，是本文的特点。走自己的路，一定要自信。要有道路自信、理论自信、体系自信，要敢于担当，真正做到‘千磨万击还坚韧，任尔东西南北风’。特色思路么。真正做到担当，不容易呀！

[1]冯・诺依曼：数学在科学和社会中的应用。大连理工大学出版社，2009.

[2]H.Weyl∶The theory of groups and quantum mechanics, Dover.1928.

[3]H.Weyl∶The classical groups;Their Invariants and representations, University press, Princeton, 1939.

[4]冯康，秦孟兆：Hamilton体系的辛计算格式。浙江科技出版社，2004.

[5]E.Hairer,Ch.Lubich and G.Wanner∶Geometric-Preserving Algorithms for Ordinary Differential Equations. Springer,2006.

[6]杰克曼(J.Jakeman)：牛顿：上帝、科学、炼金术，大连理工大学出版社，2008。原版 Newton－A beginner’s guide.

[7]钟万勰：弹性力学求解新体系。大连理工大学出版社，1995.

[8]姚伟岸，钟万勰：辛弹性力学。高等教育出版社，2003.

[9]钟万勰：力、功、能量与辛数学，3rd ed.大连理工大学出版社，2012.

[10]钟万勰：应用力学对偶体系。科学出版社，2002.

[11]钟万勰：应用力学的辛数学方法。高等教育出版社，2006.

[12]钟万勰，高强，彭海军：经典力学-辛讲，大连理工大学出版社，2013.

[13]钟万勰，欧阳华江，邓子辰：计算结构力学与最优控制。大连理工大学出版社，1993.

[14]钟万勰，吴志刚，谭述君：状态空间控制理论与计算。科学出版社，2007.

[15]希尔伯特：数学问题。大连理工大学出版社，2009.

[16]H.Goldstein, Classical mechanics, 2nd ed. Addison-Wesley, 1980.

[17]G Zhong,JE Marsden.Lie-Poisson Hamilton-Jacobi theory and Lie-Poisson integrators.Physics Letter A, 113(3)∶ 134-139,1988.

[18]高强，钟万勰：Hamilton系统的保辛-守恒积分算法。动力学与控制学报, 2009.

[19]钟万勰，高强：辛破茧。大连理工大学出版社，2012.

[20]E.Hairer&G.Wanner∶Solving ordinary differential equations II-stiff and differential- algebraic problems 2nd ed.ch.7.[M],Springer,Berl in,1996.

[21]钟万勰，姚证：时间有限元与保辛，机械强度，27(2)，2005.

[22]Q.Gao,S.J.Tan,H.W.Zhang,W.X.Zhong.Symplectic algorithms based on the principle of least action and generating functions. International Journal for Numerical Methods in Engineering, 89(4)∶ 438-508,2012.

[23]高强，钟万勰：Hamilton系统的保辛-守恒积分算法。动力学与控制学报, 2009.

[24]钟万勰，高强∶ 约束动力系统的分析结构力学积分，动力学与控制学报，4(3), 2006.

[25]杜瑞芝：数学史词典。山东教育出版社，2000.

[26]阿蒂亚：数学的统一性。大连理工大学出版.

相关链接：

祖冲之（公元429年4月20日～公元500年）是我国杰出的数学家，科学家。南北朝时期人，汉族人，字文远。生于宋文帝元嘉六年，卒于齐昏侯永元二年。祖籍范阳郡遒县（今河北涞水县）。为避战乱，祖冲之的祖父祖昌由河北迁至江南。祖昌曾任刘宋的“大匠卿”，掌管土木工程；祖冲之的父亲也在朝中做官。祖冲之从小接受家传的科学知识。青年时进入华林学省，从事学术活动。一生先后任过南徐州（今镇江市）从事史、公府参军、娄县（今昆山市东北）令、谒者仆射、长水校尉等官职。其主要贡献在数学、天文历法和机械三方面。

祖冲之算出π的真值在3.1415926和3.1415927之间，相当于精确到小数第7位，这一纪录直到1427年才被阿拉伯学者卡西所超越。他提出约率22/7和密率355/113，这一密率值是世界上最早提出的，比欧洲早1100年，所以有人主张叫它“祖率”，直到16世纪年才由荷兰人奥托得到。

（以上下载自：百度百科http∶//baike.baidu.com/ view/2122.htm）

祖冲之计算出π的真值在3.1415926和3.1415927之间，如果用割圆术计算，需要计算圆内接正49152边形才可以达到3.14159265，而以当年的计算工具显然做不到。祖冲之到底用什么方法计算到这么精确的值现在已经是个谜。