总体最小二乘方法在地震位错模型中的应用探讨

李海燕 王乐洋,2

（1.东华理工大学测绘工程学院 江西南昌 330013；2.流域生态与地理环境监测国家测绘地理信息局重点实验室 江西南昌 330013）

总体最小二乘方法在地震位错模型中的应用探讨

李海燕1王乐洋1,2

（1.东华理工大学测绘工程学院 江西南昌 330013；2.流域生态与地理环境监测国家测绘地理信息局重点实验室 江西南昌 330013）

分析了目前基于位错模型反演地震断层参数的研究现状，尝试利用总体最小二乘方法反演地震断层问题，通过探讨总体最小二乘方法在非线性反演震源参数和线性反演震源滑动分布两个方面的应用，进一步促进位错模型下地震断层参数反演的理论和应用的研究。

位错模型；总体最小二乘；震源参数；滑动分布

1 引言

地震是地球上最常见的自然现象之一，也是最严重的自然灾害之一。研究地震的手段通常有地震学、地质学、野外地质调查和大地测量方法等。地震学方法是通过地震波资料反演震源参数，由于地震波辐射场与断层的滑动量、断层破裂的速度及震源时间函数有关［1］，因此，通过地震波资料确定震源参数及地震震级通常并不能准确反映地震发生所释放的真实能量。地质学主要通过地质构造来分析断层的演化过程，这类方法涉及的时间尺度一般都是几十万、几百万甚至上亿年，无法精确反映短期的地壳活动。野外地质调查可以获得断层破裂延伸至地表时的断层走向方向及断层近似长度，而对于断层破裂深度或破裂未能延伸至地表时，该方法将无法确定震源参数。大地测量方法能够有效弥补前述几种方法的不足，特别是近二三十年，随着空间大地测量技术（如GPS、INSAR)的发展，使得获得精确的同震前后地表位置的变化成为现实，通过弹性位错理论，建立了地表形变数据和震源几何学、运动学的联系［2-4］，通过拟合地表形变数据，可以比较精确地获得断层震源参数。

本文首先介绍同震矩形位错模型，综述已有的基于位错模型的断层参数研究进展，针对目前位错模型断层参数反演大都没有考虑模型系数矩阵误差的问题，探讨了基于总体最小二乘的地震震源参数和滑动分布反演方法。

2 同震位错模型

断层位错模型是地球物理模型中描述断层运动的主要模型，有矩形位错和三角位错等。位于均匀弹性半空间的矩形位错模型是最常用的位错模型。1958年Steketee［5］首次将位错理论引入地震学中用来描述断层运动。1985年Okada系统总结了已有的研究成果，进一步推导了均匀弹性半空间介质的矩形位错理论，给出了断层矩形位错引起的地表形变关系式。位错模型已成为利用大地测量观测数据反演地震参数和震源机制非常有效的手段。

如图1，在o-xyz为断层坐标系，断层面的长度为L，宽度为W，断层深度为d，倾角为δ，断层走向α，U1，U2，U3分别是断层面沿走向、倾向和张裂方向的滑动量，假设断层坐标系原点在地面坐标系中的位置为（x0，y0），断层参数X＝［x0，y0，L，W，d，δ，α，U1，U2，U3］T其中，U1，U2，U3为的滑动参数，其余为几何参数。则断层引起的地表形变量f为

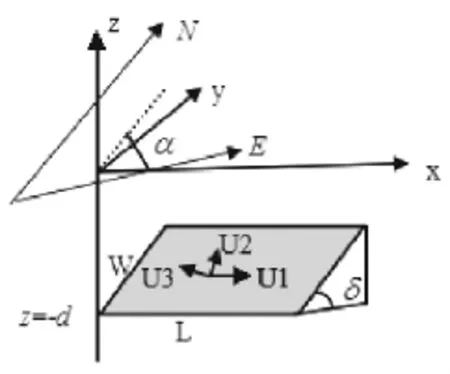
图1 均匀弹性半空间矩形位错示意图［6］

Okada矩形位错公式中，断层几何参数与地表形变量是非线性关系，而断层的滑动参数与地表形变形变量之间是线性的。所以断层参数的反演包含非线性参数反演和线性滑动分布反演。非线性反演就是在单一均匀滑动模型下，确定断层的几何参数及均匀滑动量；线性滑动分布反演是在确定断层几何参数基础上，得到破裂面上更精细的滑动量分布。通常将断层面沿断层走向和倾向方向分别适当延长，将延长后的断层面离散剖分为M个小断层片，然后通过Okada位错公式计算单位走滑和单位倾滑（1m)在每个地表观测点上产生的地表位移，由这些位移量构造N×2M阶的格林函数H。N为地表观测点个数。得到地表位移与震源参数的关系：

其中，d表示地表点形变观测值；m （2M×1阶）表示断层分别沿走向和倾向方向的滑动量；Hs和Hd分别表示其中某一小断层走滑和倾滑引起的地表位移。

3 矩形位错断层反演研究现状

3.1 非线性断层参数反演

由于地表形变值与断层参数是非常复杂的非线性关系，很难给出其线性化形式，同时线性方法对模型参数的初始值依赖性很大，所以更多的是采用非线性反演方法求解断层参数，传统的非线性反演方法有牛顿法、梯度法，还有启发式的搜索算法，如模拟退火法、遗传算法等［7］。温扬茂［6］通过获得1997年玛尼Mw7.5级地震地表点的InSAR形变数据，运用遗传算法反演了的该地震的断层参数，并用蒙特卡洛误差传递方法评定反演参数的精度；得到均匀滑动模型下反演的震级为Mw7.51级（地震矩Nm），与地震学方法得到的结果相近。李爽［8］对基于位错模型的多类数据联合反演问题进行了研究，采用区间模拟退火算法研究了地震定位问题，并利用重力数据和GPS数据，联合反演了川西鲜水河断裂带的断层参数。有学者也研究了线性化迭代反演，由于线性化得到的系数矩阵容易产生结构性扰动和受线性化误差的影响，故Bifulco等［9］利用最小范数（LN）算法来求解参数反演这一结构总体范数 （structured total least norm，STLN）问题，同时为了抵抗观测值粗差对结果的影响，采用具有抗差能力的1范数进行参数求解。并通过模拟数据验证了该算法在断层参数反演中的有效性。王乐洋等［10］在Bifulco等研究的基础上，利用InSAR数据和LN算法反演了2008年青海大柴旦Mw6.3级地震的断层参数。

3.2 断层滑动分布反演

已知断层的几何参数，那么断层面上的滑动值与观测得到的形变场之间则是线性关系，可以通过最小二乘方法来求解断层滑动分布问题。李志才等［11］基于GPS观测数据反演了汶川地震断层参数，利用弹性半空间均匀位错理论，采用有界变量最小二乘法反演了汶川地震断层滑动分布。Elliottetal［12］联合升降轨Envisat雷达影像，获得了2008年大柴旦Mw6.3级地震的InSAR数据同震形变场，采用约束最小二乘法反演了断层面的滑动分布；与Elliottet al对断层面进行均匀剖分不同的是，温扬茂等［13］利用自动剖分技术得到断层面的非均匀子块，并通过最小二乘法反演了断层的精细滑动分布；最小二乘作为最普遍、最常用的数据处理方法，已在全球范围内的中强地震滑动分布反演中得到了广泛应用。

3.3 断层参数及断层滑动分布反演算法的不足

从已有的断层参数反演研究可以发现，无论是采用非线性方法还是线性迭代方法，都只是考虑了地表形变观测值即观测向量的误差，上述的利用LN算法解决了参数反演的结构总体最小范数问题，在观测值含有粗差的情况算法具有较好抵抗粗差的能力，但是当观测向量不存在明显粗差值时，反演效果并不理想。通过分析可知，由于Okada矩形位错模型本身存在某些假设条件，这就使得模型不可避免地存在误差，进一步认为这些误差是模型参数系数矩阵的误差，此时，需要考虑系数矩阵误差对断层参数反演的影响，最小二乘方法无法处理系数矩阵和观测向量同时含有误差的情况，这时可以把最小二乘的扩展算法——总体最小二乘 （total least squares，TLS）应用于断层参数反演。

滑动分布反演中，格林函数 即模型系数矩阵是通过断层几何参数计算的单位位错在地表引起的形变，地球介质、形状、断层几何形状的复杂性、断层剖分方式对系数矩阵构成有很大影响，不同的断层几何结构对应不同的系数矩阵，分析式（2），待求参数的系数矩阵 存在误差最终将会影响滑动模型参数的反演结果。而已有滑动分布反演研究，都是基于最小二乘或约束最小二乘准则，显然，如果把总体最小二乘方法应用在滑动分布反演中，将会得到更加更加合理的滑动参数，更好地拟合地表形变位移。

4 位错模型参数的总体最小二乘反演法

最小二乘法仅在观测值存在误差时可以得到无偏最优估计值，而总体最小二乘是20世纪80年代发展起来的同时顾及系数矩阵和观测值误差的测绘数据处理方法，其理论与应用是目前国内外研究的热点问题［14］。

总体最小二乘反演的函数模型为

式中，L为观测值，eL表示观测误差，系数矩阵A及误差矩阵EA，x为待估计参数。

当观测值和系数矩阵元素等精度、不相关时，则

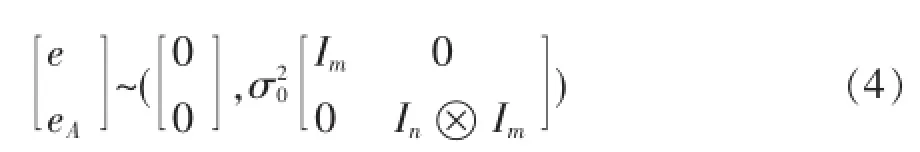
总体最小二乘的平差准则为

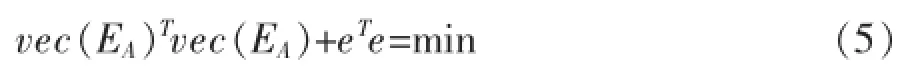
构造拉格朗日函数求条件极值，得到如下的公式［15］

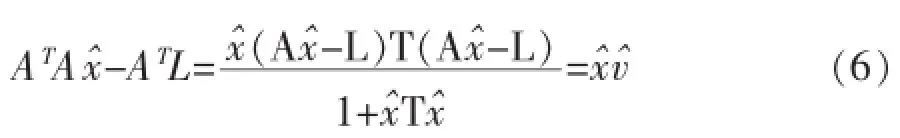
得到可待估计参数的解

当观测值与系数矩阵元素不等精度且相关时［14］，则有

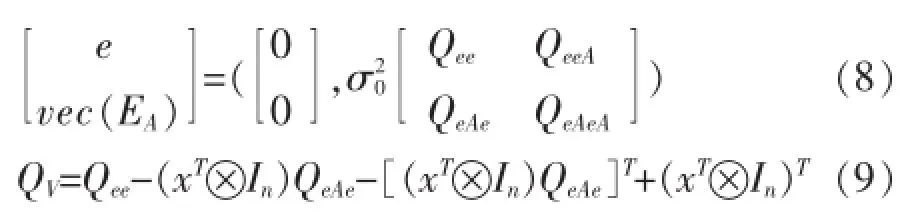
得到待估参数的加权总体最小二乘解［14］

因为等式（7）及等式（10）的右端都与参数x有关，在求解时需要迭代计算。主要步骤是把基于最小二乘的参数解作为初始值，反复计算待估参数，直至所求参数满足迭代终止条件结束。

5 结束语

地震断层参数反演、地震滑动分布反演等大地测量反演问题，通常是借助最小二乘方法完成。而模型系数矩阵和观测向量值同时存在误差时，研究总体最小二乘方法在地震断层参数反演、地震断层滑动分布等问题的应用，具有十分重要的意义。本文在综述位错模型下地震断层参数反演和断层滑动分布的研究现状的基础上，分析了位错模型中观测值和模型的误差，我们认为对于断层参数反演和滑动分布反演问题，都应同时考虑系数矩阵和观测值中的误差。因此，探讨了将总体最小二乘反演法应用于在地震位错模型参数反演，并给出了总体最小二乘反演法的一般算法。借助大地测量技术，将总体最小二乘方法应用于地震学反演问题，将是大地测量学科与地震学科交叉融合的新的研究方向。

［1］刘洋.顾及模型误差的震源参数InSAR反演［D］.博士学位论文，武汉大学，2012.

［2］OKADA Y.Surface Deformation due to Shear and Tensile Faults in a Half-space［J］.Bulletin of the Seismologica Socie-ty of America，1985，75(4):1135-1154.

［3］OKADA Y.Internal Deformation duo to Shear and Tensile Faults in a Half-space［J］.Bulletin of the Seismological Society of America，1992，82(2):1018-1140.

［4］Pollitz F.F.Coseism ic Deformation from Earthquake Faulting on A Layered Spherical Earth，Geophysical Journal International，1996，125(1):1-14.

［5］Steketee，J.A.On Volterras Dislocation in A Semi-infinite Elastic Medium，Elastic Medium Can.J.Phys.，1958，36: 192-205.

［6］温扬茂.利用InSAR资料研究若干强震的同震和震后形变［D］.博士学位论文，武汉大学，2009.

［7］王家映.地球物理反演理论［M］.高等教育出版社，2002.

［8］李爽.大地测量联合反演的模式及算法研究［D］.博士学位论文，武汉大学，2005.

［9］BIFULCO I，RAICONIG，SCARPA R.Computer Algebra Software for LeastSquaresand Total LeastNorm Inversion of Geophysical Models［J］.Computers&Geosciences，2009，35 (7):1427-1438.

［10］王乐洋，许才军，温扬茂.利用STLN和InSAR数据反演2008年青海大柴旦Mw6.3级地震断层参数［J］.测绘学报，2013，42(2):168-176.

［11］李志才，张鹏，金双根等.基于 GPS观测数据的汶川地震断层形变反演分析［J］.测绘学报，2009，38(2):108-113

［12］ELLIOTT，J.，B.PARSONS，J.JACKSON，et al.Depth Segmentation of the Seismogenic Continental Crust:the 2008 and 2009 Qaidam Earthquakes［J］.Geophysical Research Letters，2011，38(6):L06305.

［13］温扬茂，许才军，刘洋等.利用断层自动剖分计技术的2008年青海大柴旦Mw6.3级地震InSAR［J］.2012，37 (4):458-462.

［14］王乐洋.基于总体最小二乘的大地测量反演理论及应用研究［J］.测绘学报，2012，41(4):629.

［15］鲁铁定.总体最小二乘平差理论及其在测绘数据处理中的应用［D］.博士学位论文，武汉大学，2010.