一种有效提高仪器精度的建模方法

一种有效提高仪器精度的建模方法

贾云涛，胡耀元，张建永，岳伟

(北京无线电计量测试研究所，北京 100039)

摘要：提出了一种能够有效提高仪器仪表测量精度的建模方法。该模型结合改进的灰色系统和粒子群优化算法，通过测试数据对模型训练后得到仪表满量程内误差的拟合模型，进而可对仪器量程内任意测量值进行修正。通过实验证明，该模型具有经济性、实用性和准确性高的特点。

关键词：灰色系统；离子群优化算法；仪表精度

doi：10.11823/j.issn.1674-5795.2015.04.04

中图分类号：TB97；O24

收稿日期：2015-01-24

作者简介：贾云涛(1986-)，男，工程师，硕士，主要从事电学计量科研和测试工作。

An Effective Modeling Approach to Improve Meter Accuracy

JIA Yuntao，HU Yaoyuan，ZHANG Jianyong，YUE Wei

(Beijing Institute of Radio Metrology & Measurement，Beijing 100039，China)

Abstract：This paper presents a modeling approach which can effectively improve meter accuracy.This model，which combines the improved gray system and particle swarm optimization，uses a small amount of the instrument known error data as training data to get the full-scale error fitting model.Then the model can be used to amend all values in the range.The system has the advantages of economy，practicality and high accuracy proved by experiments.

Key words：gray system；particle swarm optimization；meter accuracy

0引言

仪器仪表品种繁多，已被广泛应用于工业、医疗和科研等领域中。伴随着科学技术的进步，仪器仪表越来越复杂化、集成化和高科技化。而随着使用时间的累积，仪器仪表也表现出精度下降、可维修性差的问题。由于影响仪表精度的因素具有多样性，有已知的也有未知的，这就为提高仪器的精度带来了很大的困难。

本文提出了一种粒子群非齐次灰色模型对仪表测量数据建模的方法。该模型改变了传统依靠硬件优化提高仪表精度的思想，具有通用性、经济性和有效性。

1三种建模方法

1.1灰色模型

灰色系统理论是一种用来解决信息不完备系统的数学方法，尤其适用于影响因素多样并且未知的系统[1-2]。影响仪器仪表精度的原因多种多样，有仪表电压、元器件老化、环境干扰等因素，这些因素又无法用数学量化，因此可以将仪表的误差影响系统看作是一个灰色系统进行研究[3]。

其建模方法可描述为：

设训练序列X(0)为非负序列：

X(0)={x(0)(1)，x(0)(2)，x(0)(3)，...，x(0)(n)}

式中：x(0)(k)≥0，k=1，2，…，n。

将模型训练序列进行一次累加生成，得到序列为X(1)：

X(1)={x(1)(1)，x(1)(2)，x(1)(3)，...，x(1)(n)}

(1)

Z(1)为X(1)的紧邻均值生成序列：

Z(1)={z(1)(1)，z(1)(2)，…，z(1)(n)}

(2)

式中：z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)，k=1，2，…，n。

称x(0)(k)+az(1)(k)=b为GM(1，1)模型。

若Z=(a，b)Τ为参数列，且

(3)

则可通过最小二乘估计求解微分方程x(0)(k)+az(1)(k)=b中的系数。

(4)

通过数学求解可得到白化方程的时间响应函数为

(5)

得到的式(5)即代表序列一次累加和的时间响应曲线，再进行反运算即得到训练序列的相应函数曲线，代表着训练序列的趋势轨迹。

1.2粒子群算法

粒子群算法即PSO算法(Particle Swarm Optimization)，是基于群体智能的一种寻找最优解的优化算法[4]。

应用PSO算法求解最优解有两个很重要的步骤：编码和适应度函数。PSO算法对粒子直接编码，粒子在进化过程中通过适应度函数的反馈确定最优粒子，然后通过式(6)和(7)更新粒子的速度和位置，不断逼近最优解，当达到终止条件时，停止进化。

vij(t+1)=wvij(t)+c1×rand()×(pbestij-xij(t))

+c2×rand()×(gbestj-xij(t))

(6)

xij(t+1)=xij(t)+vij(t+1)

(7)

式中：w是代表运动惯性的参数，较大的w有利于群体在更大的范围内搜索，较小的w能够保证群体收敛到最优位置，一般设置为0.8左右；c1和c2用于调整种群自身经验和社会经验在其运动中的作用，表示个体向pbest(自身最优位置)和gbest(群体最优位置)加速项的权重；rand()是介于(0，1)之间的随机数，在初始化阶段用来定义粒子的初始位置和初始速度。

1.3PSO-NGM模型

在灰色模型的基础上加入非齐次方程量，并结合粒子群优化算法求解得到组合模型，即粒子群非齐次灰色模型PSO-NGM(Particle Swarm Optimization Non-homogenous Grey Model)。将它应用于提高仪器精度上的思想就是：选取标准仪器对待测仪器量程内进行少量数据测试，将标准与被测仪器示值差作为误差，用误差数据去训练PSO-NGM模型就可以得到仪器满量程内误差模型。进而可对被测仪器满量程内任意测量值进行修正，提高仪器精度。

(8)

式中：v，C1，C2，C3，C4为待定系数。

由公式(8)可以看出，新改进的方程不仅具有原来指数的模型，还增加了直线和抛物线的拟合模型[7-8]。因此比原灰色系统更具有适用性。

2求解PSO-NGM模型

PSO-NGM模型训练的流程图如图1所示。

图1　PSO-NGM模型训练流程图

2.1归一化和反归一化

由于模型应用了灰色系统理论，而灰色理论中要求训练数据为非负。现实中仪器测量误差不可能保证总为正数，因此，需要先对原始误差数据进行归一化处理，有

(9)

式中：xmin和xmax代表数据中的最小和最大值；(0)代表归一化的最小值是0值。

得到的新数据是一系列在(0，1)范围内的归一化数据，可以用来进行模型训练。同理，在模型训练结束再进行反归一化得到复原的数据值。

2.2初始化过程

用离子群优化算法寻求最优解需要先对代表解的粒子进行初始化，包括粒子初始速度和位置、迭代次数和种群大小等。

2.3参数v，C1，C2，C3，C4的求解过程

通过粒子群算法不断迭代优化得到最优粒子v的值后，令

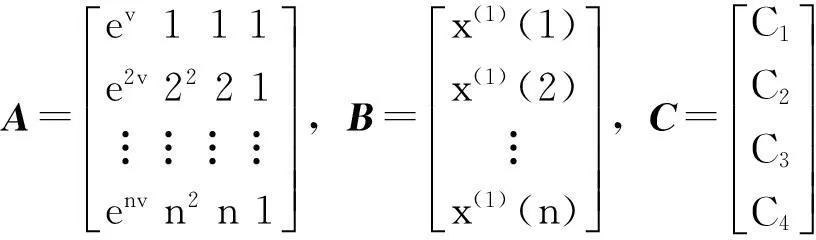
(10)

应用最小二乘法可求得参数C1，C2，C3，C4的估计值：

(11)

2.4数据还原过程

根据PSO算法和最小二乘法迭代后可得到v，C1，C2，C3，C4的值，即得到了序列累加后的拟合方程式(8)，再经过累减运算就可以得到还原序列：

(12)

2.5粒子速度和位置更新过程

每次优化后根据每个粒子对应的适应度函数大小判定粒子的优劣。求取全部粒子中的最优粒子。其他粒子根据式(6)和式(7)改变位置和速度后继续进化，直到达到指定的进化次数为止。

3PSO-NGM模型的应用分析

3.1模型训练

为了验证所建模型的正确性和有效性，我们特选取在工业生产和各大行业都普遍用到的数显表头作为研究对象。选取某型号数显表，在0～50 V量程内抽点进行电压值测量，然后应用本文模型对其误差进行训练[9]。实验中，我们选用了一组较均匀的分布于数显表量程内的电压测量点，测量时，选用标准器5720A的输出电压作为标准电压，数显表显示的电压作为测量电压。其显示值与标准值之差作为误差进行模型训练。为了证明本文模型的有效性，将修正后的结果与基本灰色模型系统修正的结果进行对比。

在0～50 V量程内包括最低、最高值点的等间距选取6个测试点。得到该数显表显示值与标准值误差如表1所示。

根据公式(9)，将绝对误差归一化到(0，1)范围，结果见表1。

表1　显示值与标准值误差及归一化结果

PSO算法在本模型中只优化一个未知解，可初始化粒子群的维数为1，初始数目为200，根据v的预估值，设置粒子初始位置和初始速度分别为(0，1)和(-0.1，0.1)内的随机数。设置终止条件为叠代次数达到500。应用已有的6个历史误差数据，选取所有训练数据拟合值与实际值的最小误差和作为适应度函数，寻求最优粒子解[10]。

3.2结果分析

使用PSO-NGM模型最终得到训练数据和拟合数据的对比如表2所示。图2显示了应用本文模型与GM模型拟合效果的对比。图3和图4分别为粒子群优化过程中适应度值的变化过程和最优粒子解的优化过程。

表2　PSO-NGM模型对训练数据的

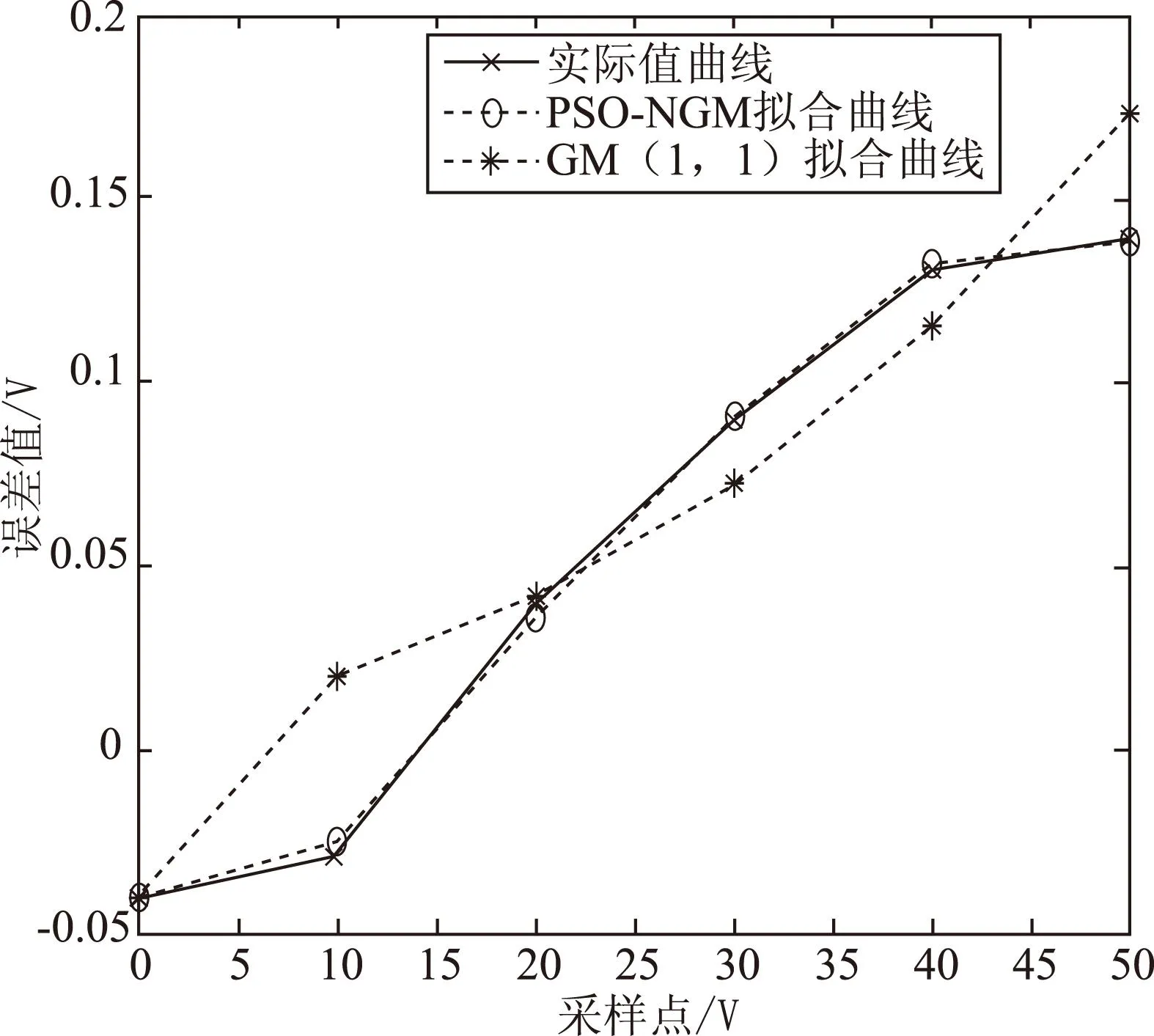
图2　PSO-NGM模型与GM(1，1)模型训练结果对比图

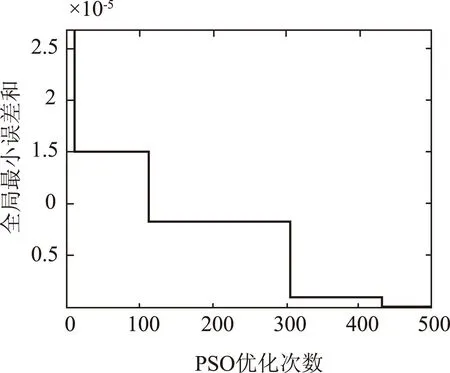
图3　PSO-NGM模型中适应度值的变化

图4　PSO-NGM模型中最优粒子的变化

从图2可以看出本文提出的PSO-NGM模型比灰色模型能更好地拟合仪器误差的曲线。

3.3模型验证

应用标准源5720A对数显表量程内一组电压点随机测量，分别应用GM(1，1)模型和PSO-NGM模型对误差进行修正。将修正结果与标准值进行比较，对比情况如表3所示。

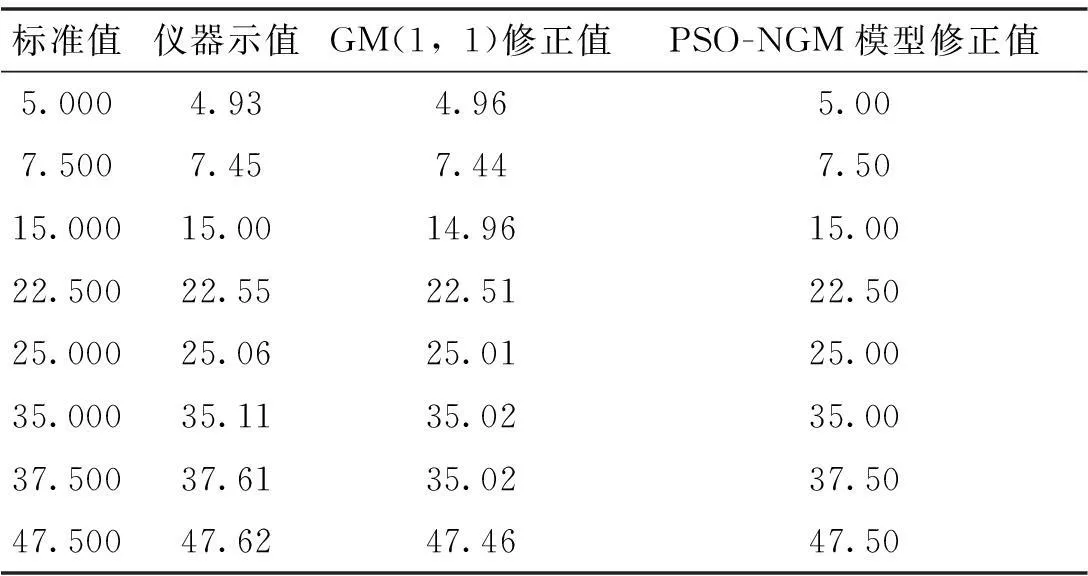
表3　PSO-NGM与GM(1，1)模型

由表3可以看出，灰色模型虽然能够对仪表误差进行少量修正，但也出现了错误修正，而本文提出的PSO-NGM模型却能够对测量结果进行准确的修正，证明该改进模型克服了原始灰色模型适用性差的缺点，能够适用于仪表误差的修正。

4总结

本文提出了一种结合灰色系统和粒子群优化算法的数学模型。该模型具有训练数据少，适用性强和精度高的优点，可应用于对仪器示值误差进行修正而不需改变仪器的硬件，具有广阔的应用前景和实用价值。

参考文献

[1] Yang G，Wu X.Fault prediction of ship machinery based on gray neural network model[C]//Proc.of the 6th IEEE International Conference on Control and Automation.Guangzhou，China：IEEE，2007：1063-1066.

[2] 彭宇，刘大同，彭喜元.故障预测与健康管理技术综述[J].电子测量与仪器学报，2010，24(1)：1-9.

[3] Cheng S，Pecht M.A fusion prognostics method for remaining useful life prediction of electronic products[C]//IEEE，2009：102-107.

[4] 唐阳山，方媛，白艳，等.基于蚁群算法的交通出行生成预测方法的研究及应用[J].辽宁工业大学学报：自然科学版，2009，(02)：108-110.

[5] 何斌，蒙清.灰色预测模型拓广方法研究[J].系统工程理论与实践，2002，9(9)：137-140.

[6] 仇芝.灰色组合模型研究与应用[D].南京：南京航空航天大学，2006.

[7] 陈鹏宇，段新胜，项翔.优化白化方程参数的新NGM(1，1，k)模型及其应用[C]//第19届灰色系统全国学术会议.北京：中国高等科学技术中心，2010：299-304.

[8]柯铧，柯科，灰色模型的扩展及应用[J].兰州理工大学学报，2013，39(6)：152-155.

[9] 潘亚林，郑树湘.应用灰色系统模型提高仪器精度[J].低温与超导，2002，30(1)：64-67.

[10] 贾云涛.基于改进灰色系统的电力电子装置故障预测技术研究[D].南京：南京航空航天大学，2012.