提高GPS基线解算质量的方法研究

引文格式： 史仲，吴任洪，王以磊. 提高GPS基线解算质量的方法研究[J].测绘通报，2015(4)：69-71.DOI:10.13474/j.cnki.11-2246.2015.0113

提高GPS基线解算质量的方法研究

史仲1，吴任洪2，王以磊3

(国核电力规划设计研究院，北京 100095)

ResearchonImprovingAccuracyofGPSBaselinesProcessing

SHIZhong，WURenhong，WANGYilei

摘要：GPS基线解成果是GPS网平差的基础数据，其质量直接影响到控制网数据处理的最终成果。基线解合格后网平差才能顺利进行。GPS静态测量费时耗力，基线解精度较差时，往往需要重测。为了避免重测，本文重点对影响GPS基线结算的主要误差源进行了分析，并给出了提高基线结算质量的方法措施。

关键词：LGO；双星；电离层模型；精密星历；基线解算

中图分类号：P228.4

收稿日期：2014-02-12; 修回日期： 2014-05-24

作者简介：史仲(1981—)，男，工程师，主要从事电力行业勘测工作。E-mail： shizhong@5npdri.com

一、引言

GPS定位测量是通过地面接收设备接收卫星传送的信息来确定地面点的三维坐标。测量结果的误差源主要有3个方面：与GPS卫星有关的误差、与信号传播有关的误差和与接收机设备有关的误差。其中卫星星历误差、电离层折射误差、对流层折射误差是影响GPS定位精度的主要因素。本文重点介绍如何在实际内业解算过程中消除以上3种误差，提高GPS基线解算质量。

二、影响GPS基线解算质量的主要误差

1. 卫星星历误差

由星历所给出的卫星在空间的位置与实际位置之差称为卫星星历误差。由于卫星在运行中要受到多种摄动力的影响，而通过地面监测站又难以充分可靠地测定这些作用力并掌握它们的作用规律，因此在星历预报时会产生较大的误差。在一个观测时间段内星历误差属系统误差特征，是一种起算数据误差。它将严重影响单点定位的精度，也是精密相对定位中的重要误差源。

2. 电离层折射误差

电离层是在距地表100~1000km的高度间，环绕地球并由带电气体(等离子体)构成的一个稀薄的大气层。当GPS信号通过电离层时，如同其他电磁波一样，信号的路径会发生弯曲，传播速度也会发生变化。因此用信号的传播时间乘以真空光速而得到的距离就会不等于卫星至接收机间的几何距离，这种偏差称为电离层折射误差。

3. 对流层折射误差

对流层是高度为40km以下的大气底层，其大气密度比电离层更大，大气状态也更复杂。对流层与地面接触并从地面得到辐射热能，其温度随高度的上升而降低，GPS信号通过对流层时，也使传播的路径发生弯曲，从而使测量距离产生偏差，这种现象产生的误差称为对流层折射误差。

三、提高基线解算质量的措施

1. 加载精密星历

卫星星历是描述卫星运动轨道的信息。GPS卫星星历分为广播星历(预报星历)和精密星历(后处理星历)。精密星历是由若干卫星跟踪站的观测数据，经事后处理向用户提供的在其观测时间内的精密轨道信息。这种星历要在观测后1～2星期才能得到，这对导航和动态定位无任何意义，但是在静态精密定位中却具有重要作用。相对于广播星历20~40m的精度而言，精密星历的精度通常在亚米级。

对于长基线而言，星历误差是影响GPS基线解算精度的重要因素。一般当基线距离超过40~50km时，加载精密星历进行基线解算时更容易得到固定解。当卫星条件不好造成基线解精度较差时，精密星历的使用能保证剔除不好卫星时段后具有更多的时间冗余度，从而保证基线处理器能搜索出整周模糊度的固定解。

精密星历一般滞后14d左右，且GPS系统和GLONASS系统的精密星历是相互独立的，需要从不同的网址进行下载(GPS精密星历的下载网址为：ftp:∥cddis.gsfc.nasa.gov/pub/gps/products/；GLONASS精密星历的下载网址为：ftp:∥cddis.gsfc.nasa.gov/pub/glonass/products/)。精密星历下载后，从基线数据处理参数中就可以设置使用精密星历来处理基线。虽然精密星历对于长基线的处理效果明显，但对于一般性的GPS工程控制网来说，其应用也可以在广播星历通过的基础上进一步提高整网的可靠性及内符合精度。

2. 双星解算

美国GPS系统由于更新速度缓慢，多颗卫星已超出了设计年限(一般为8年左右)。目前，在构成GPS系统空间部分的32颗卫星中，有近17颗卫星超期服役。在进行静态高精度数据处理时，这些“高龄”卫星的载波相位数据必然会对基线解算造成不良影响。很多测量人员都感觉到现在做静态测量时，基线解算不如以前容易通过，在观测环境不好的地区，即使提高卫星截止高度角、删除周跳时段或周跳卫星也无法获得理想的基线解结果。如果基线处理质量不好，同步环及异步环闭合差超出限差，就需要返工。

目前，很多GPS厂家发布了支持GPS和GLONASS的双星GNSSRTK系统。毋庸置疑，俄罗斯的GLONASS卫星对于提高RTK初始化速度和精度都起到了重要作用，尽管双星接收机要比单星GPS接收机贵，但其效果也逐渐得到了很多用户的认可，市场占有率在不断提高。对于双星信号，很多用户只是在使用RTK模式工作时才体会到了明显的效果。在静态数据处理时，由于大部分免费的随机后处理软件都不支持GLONASS解算，导致双星接收机的使用效果大打折扣。

LGO7.0中文版是目前为数不多的支持GLONASS静态基线解算的免费随机后处理软件。如果导入LGO软件的两个站的静态数据都是双星的，在解基线时GLONASS数据会自动参与解算。如果形成基线的两台接收机中仅一台有GLONASS数据，则GLONASS不会参与解算。

3. 使用电离层改正模型

电离层引起的无线电信号的延迟，有时可达数十米。电离层延迟是GPS测量中最严重、最棘手的误差源之一。虽然双频GPS观测数据可以通过形成电离层无关的线性组合观测值自行校正电离层延迟影响，但是这不仅增大了观测噪声的影响，也给卫星天线相位偏心、卫星钟差及卫星仪器偏差的计算和分离带来很多困难，从而间接地影响和限制了双频GPS的测量精度。

精确的电离层延迟信息(电离层模型)，不仅是单频GPS用户实现高精度改正电离层延迟影响的需求，也是双频GPS用户进一步提高测量精度的要求。

在LGO软件的数据处理参数里，当电离层模型选择“全球 / 区域模型”时，就可以用精确的电离层模型来减小电离层不确定性对基线解算的影响，从而提高基线解算的精度。数据采集时每天的电离层模型均可从瑞士波恩大学的FTP网站下载(网址：ftp:∥ftp.unibe.ch/aiub/CODE/YYYY/CODwwwwd.ION.Z)。

在使用时，把下载的电离层文件(*.ion)手动拷贝到需要的LGO项目下，然后即可进行正常的基线解算。

4. 使用对流层折射改正模型

由于对流层折射对GPS信号传播的影响情况比较复杂，一般采用改正模型进行削弱。当观测站相距不太远时(如小于20km)，由于信号通过对流层的路径相似，因此对同一卫星的同步观测值求差，可以明显地减弱对流层折射的影响。因此，这一方法在精密相对定位中广泛被应用；但是，随着同步观测站之间距离的增大，求差法的有效性也将随之降低。当距离大于100km时，对流层折射的影响就制约着GPS定位精度的提高。

四、算例

为验证上述几种措施的实际效果，通过以下实测的GPS控制网的观测数据，分别按不同的方式处理基线，并将同步环闭合差作为检验指标，对处理结果进行比较。该控制网的平均边长小于20km，按照C级网的精度标准进行观测。

图1　某地区6个GPS点的网形图

表1、表2为对图1中10条基线5个同步环4h的观测数据综合使用上述3种措施(双星+电离层模型+精密星历)处理的闭合差结果。

表1　广播星历下4种解算的结果　 m

表1中的4组数据表明，在使用广播星历时，GPS+电离层模型的效果要优于仅用GPS解算，但电离层模型不一定能解决所有的超限同步环(如环5)；而用双星数据解算时，超限的闭合环亦合格，说明双星对问题基线及同步环闭合差的改善效果最为明显，双星+电离层模型的组合效果与仅用双星解算的效果差别不大，两者闭合差的变化量在4mm左右。

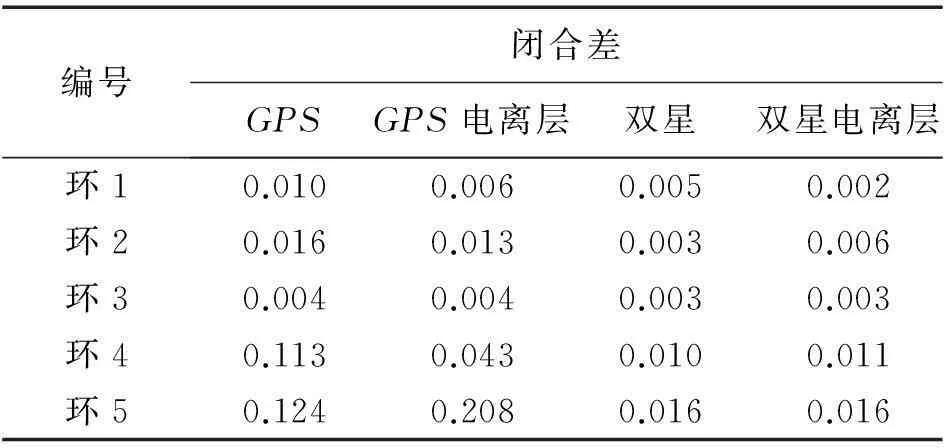
表2　精密星历下4种解算的结果　 m

将表2与表1进行对比可以看出，精密星历的引入对数据解算结果的影响有限，与广播星历解算的对应值基本一致，这也说明精密星历虽然不一定能明显改善解算结果，但也不会对结果产生负面影响。精密星历对提高基线解质量来说并非毫无用处，只是由于该网的基线长度不算太长(都在20km以内)，而精密星历往往对长基线(50~80km左右)的解算会有比较明显的效果。

五、结束语

当静态观测时间较长时，是否用精密星历或电离层模型模型都对结果影响不大。但对于观测时段较短或则存在外部干扰时，以上办法对于提高基线解算质量都有比较明显的效果。相比较而言，双星的静态数据对于提高基线解算效果最为显著，电离层模型在观测时长小于45min或电离层较活跃时会有一定的效果。精密星历对提高解算短基线的精度影响不大，对于长基线效果会有一定效果。当在GPS静态网基线解算出现“问题”基线时，往往需要把以上几种方法结合起来，才能得到精度和可靠性都符合要求的结果。

除此之外，LGO软件还提供了很多的基线解算分析工具，功能强大，对于处理“问题基线”同样很有效果，深入了解、灵活应用LGO软件的各种功能，对于提高GPS外业工作效率，减少重测和返工，都具有非常现实的意义。

参考文献：

[1]LeicaGeosystemsAG.LGO7.0OnlineHelpManual[EB/OL].[2014-01-15].http:∥www.surveyequipment.com/gpstps-pc-software?chapter=1#.Uvrj8vujAeo.

[2]刘大杰. 全球定位系统(GPS)的原理及数据处理[M].上海:同济大学出版社,1996.

[3]乔仰文,赵长胜.GPS卫星定位原理及其在测绘中的应用[M].北京:教育科学出版社,2003.

[4]周勇，彭云.GPS星历精度对基线解算的影响[J].桂林工学院学报，2004，24(2):192-194.

[5]袁运斌，霍星亮，欧吉坤.精确求定GPS信号的电离层延迟的模型与方法研究[J].自然科学进展，2006，16(1)：40-48.

[6]杨润书，周红云.广播星历与精密星历对GPS基线解算和网平差的影响[J].地矿测绘，2010,26(4):7-9.

[7]杨润书.GPS基线解算的优化技术[J].测绘通报,2005(5):36-39.

[8]张清志，唐文清，李军.GPS卫星星历对测站及基线精度的影响[J].沉积与特提斯地质,2012,32(3):106-112.

[9]孙小荣，李海陵，王宇杰，等．广播星历和精密星历解算GPS基线成果的比较分析[J]． 现代测绘，2009，32(3):45-46.

[10]张延同，胡志红.合肥盆地GPS控制网的建立[J]. 测绘通报,2002(4)：25-27.

[11]边少峰，李文魁.卫星导航系统概论[M].北京：电子工业出版社，2005.