基于Monte Carlo网络的进度风险分析

蔡永勇++吕超贤++许燕++徐永红

摘要：由于现代项目的大型化和项目复杂性的不断增加，如何对项目的进度进行正确的预测和合理的规划已经受到越来越多的关注，传统的CPM/PERT方法已经难以满足人们的需要。本文对现有的进度评估技术进行了改进，加入了对四种任务逻辑关系的支持，并给出了资源冲突时的解决策略，设计并实现了一个面向复杂项目的进度风险评估方法，不仅支持多种随机变量的抽样，还能够给出工期优化策略，旨在帮助项目决策者根据仿真结果识别关键任务，以此来制定合理的工期计划。

关键词：进度风险评估；Monte Carlo网络；成本风险

中图分类号：TP391. 41

文献标识码：A

DOI： 10.3969/j.issn.1003-6970.2015.07.013

0 引言

根据现在美国项目管理协会的划分，风险管理过程分为规划风险管理、风险识别、实施定性风险分析、实施定量风险分析、规划风险应对、监控风险6个部分。而风险类型又主要有费用风险、进度风险、技术风险、计划风险等等。而项目在实际运作中，会受到诸多因素的影响。项目在施工过程中，人们往往将项目的进度作为最重要的控制目标，尤其是在大型工程项目的建设上，项目进度常被当做首要控制目标。

“Monte Carlo”一词源于摩纳哥的Monte Carlo赌场，赌场中“轮盘赌”之类的游戏与概率、随机抽样等有着类似的原理。Monte Carlo网络法亦称为随机抽样法，该法是实验数学的一个分支，是利用随机数进行统计实验来解算数学问题的方法。Monte Carlo网络的本质是对随机变量进行概率分布估计，具体的做法是用随机抽样来抽取符合特定分布的伪随机数，采用某种特定方法产生随机数和随机变量，仿真随机事件，对结果进行统计处理，从而得到问题的解。

Monte Carlo网络方法根据事物运动过程的数量和几何特征，在确定的分布中提取随机变量，进行多次抽样。在具体的实验中，模拟次数越多，Monte Carlo网络的精度也越高。

Monte Carlo网络的基本步骤是：（1）通过敏感性分析，确定风险变量。（2）构造风险变量的概率分布模型。（3）根据项目特点确定风险问题的评价指标，建立风险问题数学模型。（4）根据项目投资者的风险承受能力确定模拟次数N。（5）对各个备选方案风险变量进行随机抽样。（6）将各个备选方案的风险变量的随机抽样值根据所建立的数学模型或者计算流程图计算出项目评价基础数据。（7）对各个备选方案风险变量进行N次重复抽样，产生各方案的抽样值。（8）对各方案的结果进行统计分析。

本文应用并优化Monte Carlo网络算法，包括随机变量的生成以及考虑任务逻辑关系和资源的关键链算法且提出了当资源冲突时的解决方法。

1 随机变量的生成

在进度管理中，任务的工时是一种期望值，应当作随机变量来处理。而在传统的CPM方法中，工时直接被当作常量来处理，到了PERT方法中，开始认为工时服从Beta分布，进而通过估算最低值a，最可能值m，以及最高值b，来近似求得服从Beta分布的工时的均值 ，以及方差 ，但依旧误差很大。鉴于现代复杂项目任务的复杂性，通过随机方法来进行模拟能够有效减少误差。

本文采用Monte Carlo方法，通过构造概率模型并对它进行随机试验来解算数学问题。Monte Carlo的核心在于根据已知分布产生简单子样，也就是产生一系列相互独立且服从总体分布的随机数。计算机高级语言都支持随机数的产生，且可以认为它们是相互独立且服从均匀分布的数列，因此剩下的工作就是根据这些服从均匀分布的数列产生服从特定分布的数列。

因为实际项目中任务服从的分布以连续分布为主，因此下面所述的方法和分布若无特殊说明，均是建立在连续分布的基础上。对于形如 ，的累积分布函数，目前主要的抽样方法有直接抽样法（又叫反函数法，逆变换法），合成法和筛选法。

本文针对三种特定的分布分别给出抽样原理和实现步骤。

1.1 三角分布抽样

三角分布亦称辛普森（Simpson）分布，是一种连续概率分布函数。三角分布通常可以看作一种经验性的描述，比如可以用来描述人口，特别是当数据之间的关系已知而数据量又非常少的时候，它通过最小值、最大值和最可能的值来建立模型进行经验性的判断。三角分布的累积分布函数（cumulativedistribution function）如（1）式，其中a为低限、c为众数、b为上限，其中a代表的含义是出现最小值的概率，b代表的含义是出现最大值的概率，c代表的含义是出现最可能的值的概率：

（1）通过随机数生成器生成服从U（O，1）的随机数U。

（2）计算厂（x）的反函数f^-1（x），获取样本x=f^-1（U）

因此，对于生成的随机数U，每次样本x取值应该为

1.2 正态分布抽样正态分布又名高斯分布，其概率密度函数为

，而累计积分函数为 ，因为 无法直接计算，可见直接抽样法对正太分布来说比较困难，目前主要的方法是进行近似计算，比如中提出的算法可以精确到小数点后16位。不过因为步骤繁琐，难以编程实现，因此这里选用的是Box-Muller方法来进行抽样。Box-Muller算法隐含的原理虽然深奥，但结论却是相当简单：

（1）通过随机数生成器生成服从U（O，1）的随机数U和V

（2）计算 和

其中X和Y分别服从标准正太分布且相互独立，可以任选其一作为抽样结果，假设选取X作为结果，根据正态分布的特性，通过计算Xxa+μ即可，就可以得到服从N（μ，σ）的抽样。

1.3 β分布抽样

β分布是一个作为伯努利分布和二项式分布的共轭先验分布的密度函数，在机器学习和数理统计学中有重要应用，主要用途就是给受限于有限长度的随机变量来建立模型。β累积分布函数 ，可以看出直接抽样也是比较困难的，比较常用的方法有合成法和接受拒绝法。其中合成法依赖的定理是如果x和Y相互独立，且x服从 ，Y服从 ，那么 服从B（a，β）分布。虽然β分布难以直接抽样，但γ分布容易抽样，因此可以通过γ分布来合成β分布，不过γ分布一般通过大量指数分布来合成，也比较耗时，这里采用冯诺依曼提出的接受.拒绝的方法来进行抽样。endprint

首先满足β分布的概率密度函数为 ，其中O3（l-x）²。

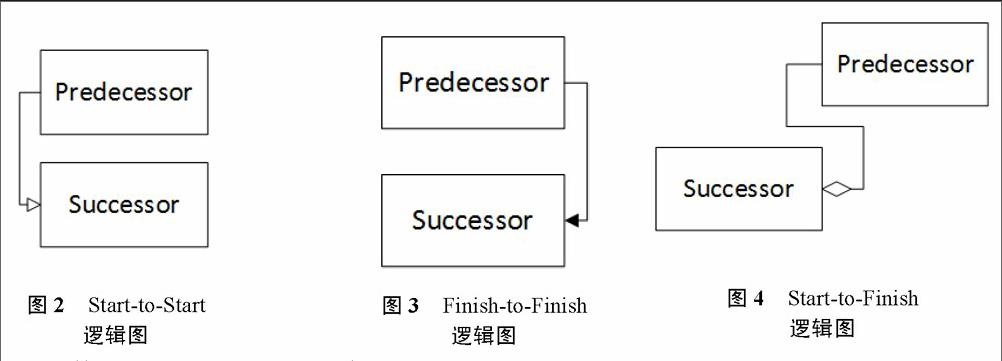
（1）选择函数g（y），这里选择g（y）=1，0≤y

（2）找a，使得对于所有的x，均有 ，这里 ，为了方便，取a=3。

（3）生成y～U（O，1），U～U（O，1），并且判断U是否大于20Y³（1-Y）²，如果成立Y则为本次抽样结果，否则重新生成y和U，直至满足条件为止。

2 任务逻辑关系转换和进度推进仿真算法

在网络计划技术中，通常对图的研究都仅限于FS型，包括各种经典的图论算法，也都是把前后节点之间的关系当作FS型来处理。而在实际的项目管理中，前驱任务和后继任务之间的逻辑关系一共有四种，分别是：

①Finish-to-Start（FS）：如图1，前辈节点必须先结束，后继结点才能够开始。

② Start-to-Start（SS）：如图2，前辈节点必须先开始，后继结点才能够开始。以修路为例，虽然可以一边挖路一边铺沥青，但是必须要先开始挖路再开始铺沥青。

③Finish-to-Finish（FF）：如图3，前辈节点必须先结束，后继结点才能够结束。以铺线为例，任务一往一栋楼中铺线，任务二是检查楼中铺的线，那么必须等到铺线完成后，检查工作才可能停止。

④Start-to- Finish（SF）：如图4，前辈节点必须先开始，后继结点才能够结束。还是以修房子为例，假设修房子必须用到材料A，那么直到材料A送达前，修房子都不可能结束。

基于传统CPM算法的启发，本文设计了兼容这四种任务逻辑关系的进度推进仿真算法。

首先，对算法中涉及到的类型进行定义，用一个五元组Task（distri，per， prog，expS，expE，accS，accE）来表示项目中的任务。

其中，distri属性和per属性属于任务的固有属性，distri属性代表Task的分布类型，比如三角分布、正态分布和β分布；per属性代表的是任务的工时。而后面五个属性是为了在仿真算法中记录中间结果添加的属性，其中prog属性代表仿真过程中当前任务的进度，初始值为0，随着时间的推进，prog不断变大，当prog的值等于任务的工时per时，该任务完成（但还不一定结束，还需要参考accE属性）；expS属性代表的是任务开始期望数，属性accS代表的是任务的当前开始期望数，也就是当accS的值等于expS值时，任务可以开始；同理定义expE为任务结束期望数，而accE代表任务的当前结束期望数，当任务的当前结束期望数达到expE后，任务才可以结束。

接着用一个三元组Link（preTask，sucTask，type）来表示任务之间的逻辑关系，其中preTask属性代表的是该关系连接的前驱Task，而sucTask属性代表的是与之相连的后继Task，属性type则代表了该关系的逻辑类型。

算法思路：对所有的Link进行了遍历，如果Link是FS或者SS类型，因为前驱任务的开始或者结束才会导致后继任务的开始，所以后继任务的开始期望数需要增加。同理如果Link的类型是FF或者SF型，那么需要增加后继任务的结束期望数。核心思想是根据任务的开始期望数和结束期望数来判断任务的开始和结束。算法采用了模拟的思想，即每次将所有任务向前推进一定的时间t_min（也就是找出那些距离完成时间最短的任务，t_min为它们的总工时减去当前进度），然后将这些任务的prog属性加上t_min代表时间向前推进。

本文对Task定义了三种状态，分别用三个集合加以表示，TR为初始任务的集合，包含的是还未开始的任务，初始为所有的任务集合。TP为进行中任务的集合，当任务的当前开始期望数达标后，认为任务可以开始，这时将任务从TR移动到TP中，代表任务开始。TF为已经结束任务的集合，当任务可以结束时，将任务移动至该集合。

在算法中，每循环一次就相当于一次时间的推进，且在循环中，算法会检查和修改任务的状态。其中，时间的推进用prog属性来表示，通过从零增加prog的值到其工时，代表任务从开始到结束。而检查任务是否能够开始则通过判断任务的当前开始期望数accS是否等于其开始期望数expS，检查任务是否能够结束则通过判断任务的当前结束期望数accE是否等于其结束期望数expE。每当一个任务开始的时候，都需要对其后继任务进行修改，如果它们之间的关系为SS型，则将后继任务的accS属性加1，如果它们之间的关系为SF型，则将后继任务的accE属性加1。同理每当一个任务结束的时候，需要对其后继任务进行更新，如果它们之间的关系为FS型，则将后继任务的accS属性加1，如果它们之间的关系为FF型，则将后继任务的accE属性加1。

3 基于全拓扑排序的资源冲突解决策略

在考虑资源的情况下，任务执行的逻辑顺序不一定就是任务执行的实际顺序，关键任务工时的和也并非一定等于总工期。因此需要对第2节中的进度推进仿真算法进行改进。由于考虑资源的冲突，此时关键路径不再是唯一制约进度的因素，非关键路径上的任务也可以由于资源缺乏而拖延总工期。跟关键链法不同，本文的焦点是放在总工期的计算上，而上述算法也是抛弃了原来关键路径的思想，以模拟的角度来考虑问题，以最小任务工时为单位，每次计算往前推进时间。但是，本法与关键链的思想并不矛盾，同样可以往关键任务和非关键任务两端加上缓冲时间更精确的为项目管理者提供进度规划方面的建议，本文算法相当于为关键链提供了一个可行的拉动式进度计划方案。

当调用进度推进仿真算法时可以发现，资源冲突的问题其实可以等价于任务优先级的问题，即有多个任务并行时，先将资源优先分配给哪个任务，拥有资源的任务可以随着时间的推进而推进，而缺少资源的任务虽然在任务进行集合Tp中，但是却不往前推进时间（即每次prog属性不变）。因此问题被等价到了任务的优先级上，一般来说，在设置任务属性的时候，也会一起设置任务的优先级，而对于设置了相同优先级的任务，可以通过枚举的方式，进而运行进度推进仿真算法。具体的步骤是：

（1）首先求出任务网络图所有的拓扑排序序列，每一个序列就相当于一种潜在的任务优先级序列，通过回溯来找出所有拓扑排序序列的算法。

（2）对上述求得的序列进行优化，因为如果任务数目较多且任务逻辑关系复杂，全拓扑排序的结果可能非常大，甚至达到百万的数量级，使得实际程序的运行效率低下。不过所幸实际中任务之间往往存在着各种约束，通过这些约束就能够去除绝大部分的无用序列，从而使程序的效率得到保障。

4 进度更改算法

进度更改这里主要指的进行进度的压缩，假设平均总工期为K，用户设置的目标工期为M，若M

如果考虑任务的权重便可以照葫芦画瓢进行算法设计，假设当前有t₁，t₂，¨，t_n那个任务，每个任务的权重分别为P₁，P₂，…，P_n，其中关键任务为t_c1，t_c2，…，t_cn，它们的权重为P_c1，P_c2，¨，，p_cn，这里权重代表的是可压缩性，即权重的数值越大，任务的可压缩性越强。

在进度压缩的过程中，重点应该放在关键任务上，只需要对它们进行压缩，但是需要注意压缩过程关键路径不应该发生改变，那么当在压缩关键任务时，只需要保证关键任务的工时即使被压缩后也应该是同时刻并行任务中最大的即可，所以根据上述一样的思路，只是在压缩过程中按照每个任务的权重来进行压缩，而显然，因为只考虑关键任务，对于t_ci，应该将工时压缩到 ，此时若关键

任务工时小于非关键任务的工时，那么强制将非关键任务的工时减小到关键任务的工时，可见只需要稍稍修改ShrinkHours算法，将压缩任务时的语句改为按照权重来进行压缩即可。

最后在仿真完成结束后，需要根据已经保存的仿真中间信息，对项目的进度风险进行预估。假设进行了N次仿真，那么就记录了N个工期，根据大数定理，当N足够大时（一般取N为2000到10000次），便可以用这N个样本值来代替实际值。项目风险同样通过这N个样本值来进行计算，本文主要通过总工期区间统计图和进度风险图来对风险进行评估。其中，总工期区间统计图表示的是N个总工期样本值的分布情况，等价于之前设置的每个任务工时服从分布之和，也就是它们的组合分布，而该分布的期望则代表了最可能出现的总工期。进度风险图表示的是在不同总工期约束下，项目完成的风险（即失败率）。对于在工期M下的进度风险，计算公式为 。也就是统计总工期小于等于M的个数，再用1减去其占总个数N的比例。

5 结论

由于现代项目的大型化和项目复杂性的不断增加，如何对项目的进度进行正确的预测和合理的规划已经受到越来越多的关注，传统的CPM/PERT方法已经难以满足人们的需要。本文对现有的进度评估技术进行了改进，加入了对四种任务逻辑关系的支持，并给出了资源冲突时的解决策略，设计并实现了一个面向复杂项目的进度风险评估方法，不仅支持多种随机变量的抽样，还能够给出工期优化策略，旨在帮助项目决策者根据仿真结果识别关键任务，以此来制定合理的工期计划。