基于并联FIR 滤波器组的Hammerstein 预失真器*

佀秀杰，韩丽茹，曹 振

(1.辽宁石油化工大学 信息与控制工程学院，辽宁 抚顺 113001;2.浙江水利水电学院，杭州 310018)

1 引言

为了适应现代通信技术的发展，现代通信系统多采用具有非恒包络、高峰均比的宽带信号。当这些具有非恒包络特点的通信信号通过射频功率放大器(Power Amplifier，PA)时，不仅加重了PA 的非线性失真(Nonlinear Distortion，NLD)程度，而且使得PA 的记忆效性不能再被忽视。PA 的记忆效应除了引起了系统更严重的带内失真和带外失真，还增加了系统误码率(Symbol Error Rate，SER)和相邻信道之间的相互干扰［1－2］。预失真技术是目前补偿PA非线性失真的有效技术之一，该技术通过在PA 前级联一个与PA 特性相反的预失真器(Predistorter，PD)达到线性化目的。传统的PD 仅考虑了PA 的非线性失真而忽略了PA 记忆效应，因此不能很好地补偿带记忆效应PA 的非线性失真。目前，对有记忆预失真器的研究是这一领域的热点。

应用预失真技术补偿对带记忆效应PA 的非线性失真，对PA 逆特性描述的精确程度，即预失真器建模的准确性和系统参数的辨识算法直接影响该技术的线性化效果。预失真器建模的关键在于该模型对PA 逆记忆特性的描述能力，而良好的辨识算法性能是快速稳定实现预失真器对PA 线性化的保证。目前，PD 多采用记忆多项式模型［3－4］和Hammerstein 模型［5］来补偿带记忆效应PA 的非线性失真。记忆多项式模型是Volterra 级数模型的一种简化模型，由于该模型仅保留Volterra 级数核函数对角线部分，因此无法充分描述PA 的逆记忆效应，并且该模型保留了Volterra 级数模型只在有限系统输入幅度范围内收敛的问题。为了避免这些Volterra级数核的估计和收敛性问题，Hammerstein 模型被用于对预失真器的设计。Hammerstein 模型采用了和Wiener 模型一样的两箱结构，不同点在于它是由非线性系统级联线性系统而成，分别用来描述PA 的非线性特性以及记忆效应的逆特性。目前，基于该模型的预失真器多采用查找表、多项式作为非线性子系统，采用高阶的FIR 滤波器作为其线性子系统。但是，高阶FIR 滤波器对PA 的逆记忆效应特性描述不充分，且降低了PD 辨识算法的收敛速度。

已有研究人员在Hammerstein 模型的实现形式和结构上进行改进，取得了一些进展。例如，利用人工神经网络来实现的扩展的Hammerstein 模型［6］、由无记忆强非线性模块级联弱非线性模块而成的类Hammerstein 预失真器［7］、基于滤波器组的平行Hammerstein 预失真器［8］、采用查找表级联滤波器矩阵来实现Hammerstein 预失真器［9］等。但是，这些扩展的或改进的Hammerstein 模型提高了模型的复杂度(以模型含参数的个数来表征)，且使得模型结构更加复杂，辨识也更加困难。

本文针对Hammerstein 预失真器存在的以上问题，提出一种改进的Hammerstein 预失真器(由查找表级联一个具有并联结构的低阶FIR 滤波器)，并给出该PD 的辨识算法。仿真实验及分析证明，本文提出的PD 能够高效地实现对带记忆效应PA 的非线性失真补偿。

2 Hammerstein 预失真器

Hammerstein 模型的结构如图1 所示，它具有与Wiener 模型一样的两箱结构，但不同的是它由无记忆非线性子系统(NL)级联线性子系统组成，其中线性子系统一般指线性时不变系统(LTI)。

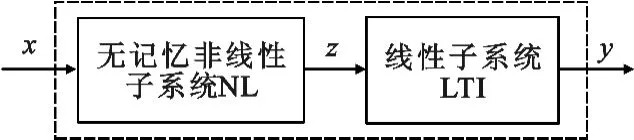
图1 Hammerstein 模型结构Fig.1 Structure of the Hammerstein model

当预失真器采用Hammerstein 模型时，其两个子系统分别用于补偿PA 的非线性和记忆效应引起的失真，因此两个子系统的系统函数是PA 系统函数的反函数。

为了获得PA 的逆特性，一般采用Wiener 模型PA 进行建模，这是因为Wiener 模型是比较成熟的PA 模型，且具有与Hammerstein 模型相对称的结构。PA 的非线性可以由多项式或查找表(Lookup Table，LUT)表示，而记忆效应通常由FIR 滤波器表示。假设Wiener 模型由FIR 滤波器级联LUT 组成，FIR 滤波器可以由转移函数H(z)来描述［10］:

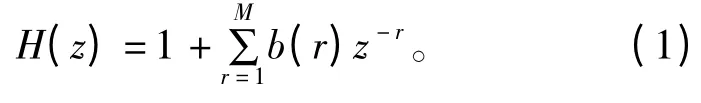
式中，b(r)为实系数。

Hammerstein 预失真器线性子系统与Wiener PA的线性子系统互逆，因此，Hammerstein 预失真器线性子系统的转移函数应该具有如下形式:

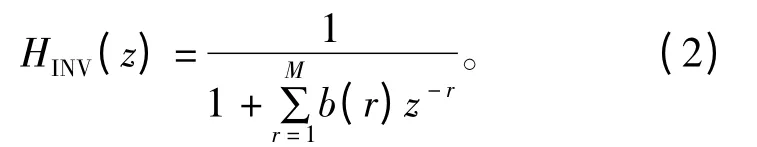
由此可知，Hammerstein 预失真器的线性子系统是一个IIR 滤波器。但是，因为IIR 滤波器本身固有的反馈特性导致系统不稳定等问题，一般采用高阶的FIR 滤波器来代替，但也由此降低了Hammerstein 预失真器对PA 逆记忆效应的补偿能力。

3 改进的Hammerstein 预失真器

为了提高Hammerstein 预失真器对PA 记忆效应的补偿能力，本文提出了一种Hammerstein 预失真器，该预失真器采用LUT 和并联的FIR 滤波器组作为其实现形式。

令z－1=x，则式(2)可以表示为

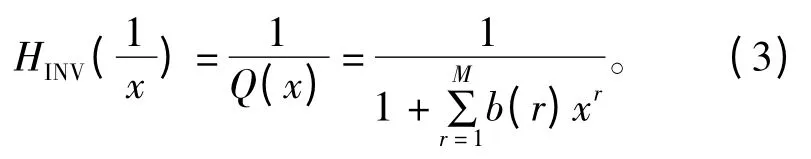
根据代数知识，有理真分式必定可以表示成若干部分分式之和，对分母Q(x)在实系数内作标准分解:

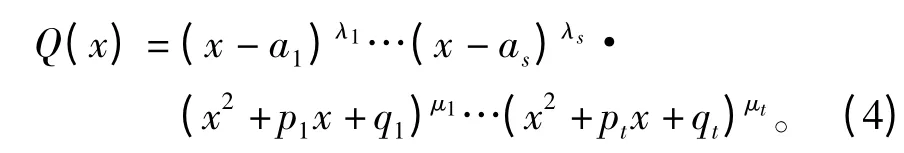
式中，b(1)=1，λi，μj(i=1，2，…，s;j=1，2，…，t)均为自然数，而且

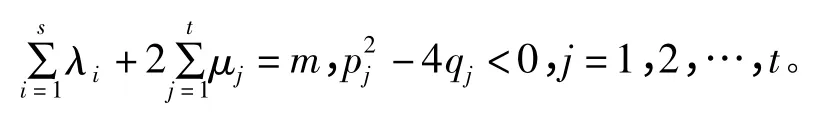
根据分母的各个因式分别写出与之相应的部分分式:对于每个形如(x－a)k的因式，它所对应的部分分式是

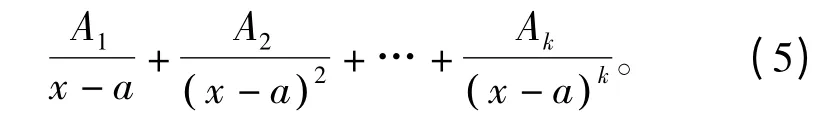
因此，可以将公式(3)作如下分解:

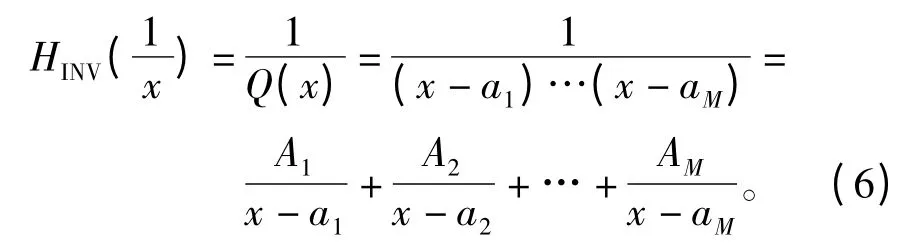
上式可以整理为

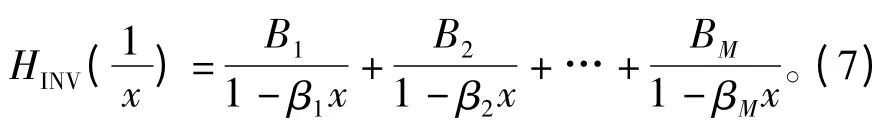
式中，Bi=－Ai/ai，βi=－1/ai。

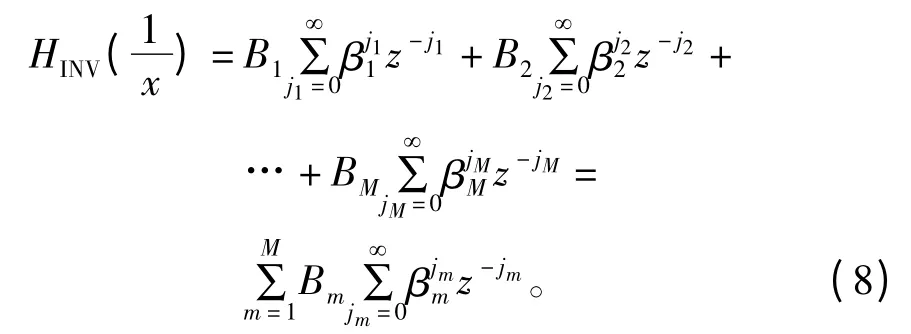
假设Hammerstein 预失真器线性子系统的输入输出分别为xl(n)和xlf(n)，对应的Z 变换为Xl(z)和Xlf(z)，因此有

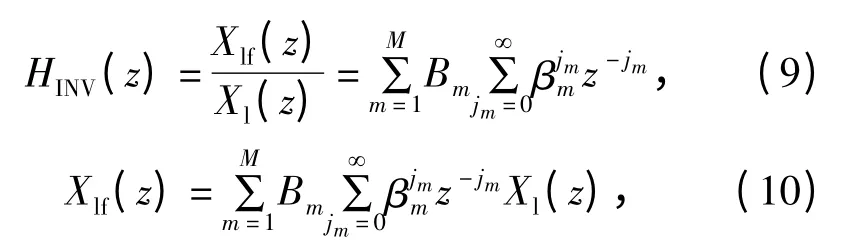
时域表示为

对上式进行截断处理得到

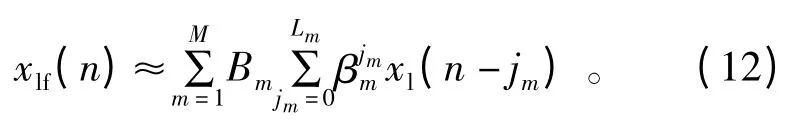
式中，Lm为第m 个FIR 滤波器的长度。

由上述分析可知，Hammerstein 预失真器中线性子系统可由M 个长度分别为Lm的并联FIR 滤波器组来实现，Hammerstein 预失真器的结构如图2 所示。

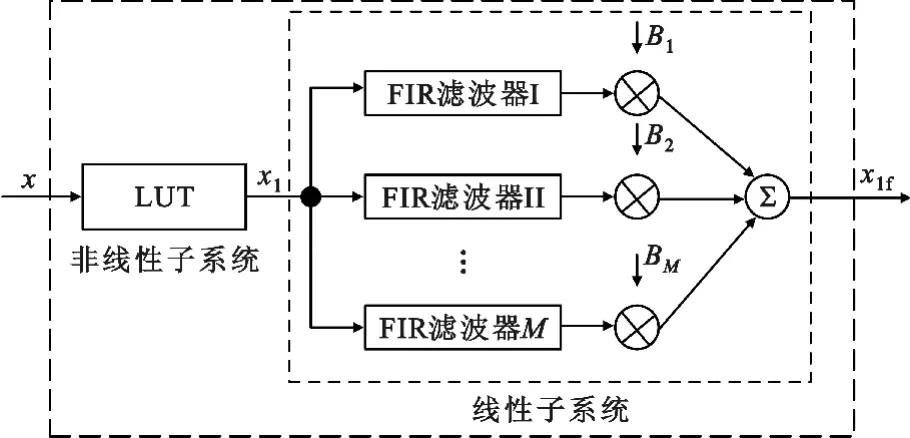
图2 Hammerstein 预失真器结构Fig.2 Hammerstein predistorter structure

4 辨识算法

为了有效辨识本文提出的Hammerstein 预失真器，本文提出一种两步辨识算法，即先离线辨识LUT，在较好地修正PA 的非线性失真的前提下，利用并联的FIR 滤波器组克服PA 的记忆效应。

4.1 LUT 的辨识

因为PA 的非线性特性是其本身特性的反映，不受如温度等外界因素的影响，因此可以离线进行处理。本文采用如图3 所示的结构来辨识Hammerstein 预失真器中LUT 存储的增益值。

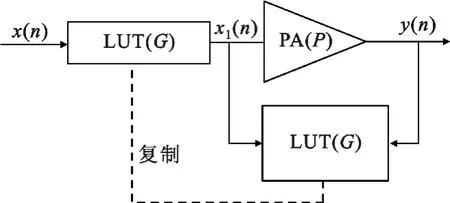
图3 LUT 的辨识结构Fig.3 LUT identification structure

由图3 可知，PA 的输入xl(n)、输出y(n)分别为LUT 的输出和输入，因此可以进一步得到对应每一个LUT 输入信号的复增益的幅值| G(n)|=|xl(n)|/|y(n)|和相位Δθ(n)=θxl(n)－ θy(n)。因为PA 的记忆效应，使得对应某个输入信号的输出值不确定，表现为调幅/调幅(AM/AM)和调幅/调相(AM/PM)曲线的扩散。为了获取PD 的非线性特性，本文首先用一组训练序列激励PA，得到LUT 的输入y 和输出xl数据，并对其进行如下处理。

以求解LUT 中复增益的幅值为例对本文算法进行说明，预失真器的AM/AM 曲线如图4 所示。

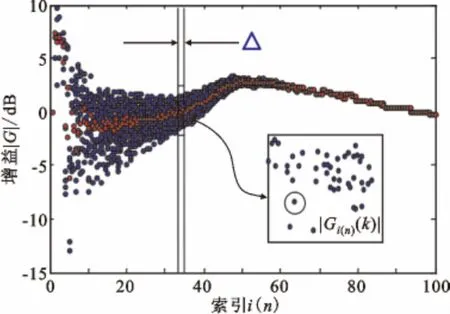
图4 幅值增益曲线Fig.4 Amplitude gain curves

对输入信号幅值进行均匀量化得到LUT 的索引值

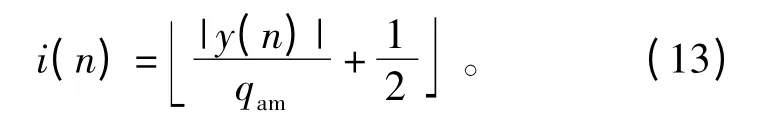
式中，|y(n)|∈ [|y(n)|min，|y(n)|max];qam为量化步长，qam=，Nam为划分的区间个数。

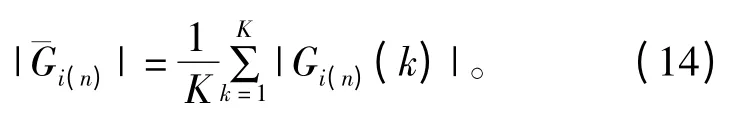
需要提出的是，区间划分的越细算法精度越高，但是可能出现某个或某些区间没有增益值，即K=0，为了使得到的AM/AM 曲线光滑，需要对进行进一步处理，如采用指数移动平均(EWMA)算法，可以得到

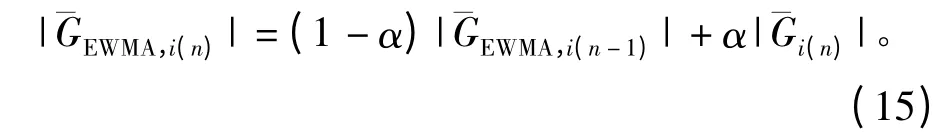
式中，α 为加权系数，取值范围为(0，1)。

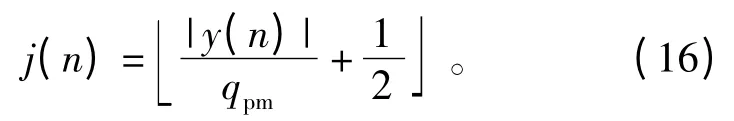
式中，qpm为量化步长，qpm=Npm为划分的区间个数。

因此，可以得到“后失真器”中LUT 的输出为

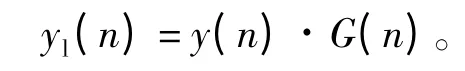
4.2 线性子系统的辨识

因为PA 的记忆效应受温度、器件老化等外界因素的影响，需要PD 能够对PA 的记忆效应进行跟踪补偿，所以对本文提出的Hammerstein 预失真器的线性子系统进行在线自适应辨识。

将并联加权系数Bm吸收入到FIR 滤波器的系数中，公式(12)可以写为

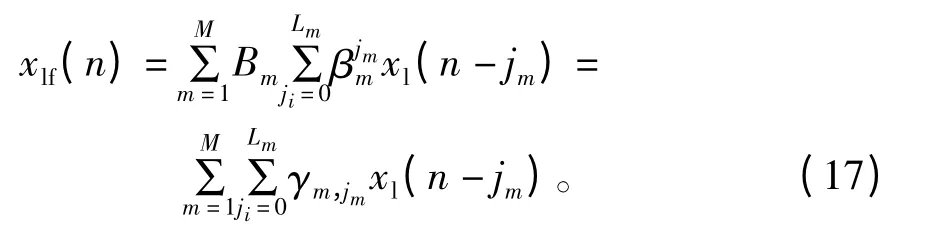
在非线性子系统得到很好辨识的基础上，采用间接学习结构对Hammerstein 预失真器中的线性子系统进行辨识，如图5 所示。

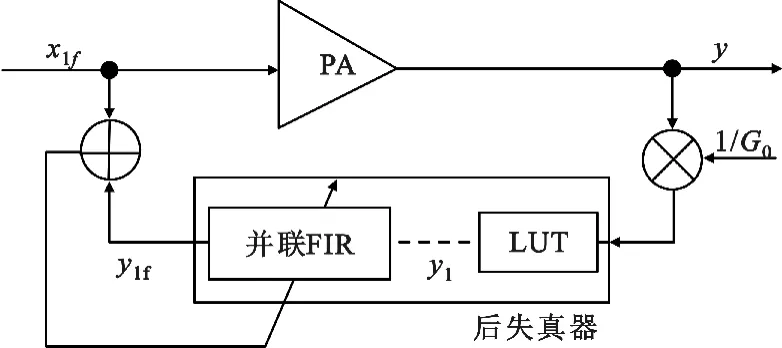
图5 线性系统更新结构Fig.5 Identification structure of the linear system

本文根据最小均方(Least Mean Square，LMS)算法对并联FIR 滤波器组参数进行更新，在第k+1 次迭代时，参数更新公式如下:

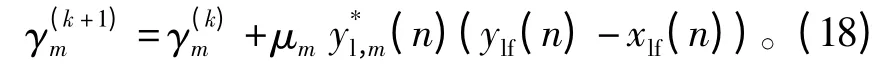
式中，μm为第m 个FIR 滤波器的更新步长，γm=［γm，0γm，1…］T和yl，m=［yl，m(n)yl，m(n－1)…yl，m(n－Lm+1)］T分别是第m 个FIR 滤波器的参数向量和输入向量，ylf是“后失真器”的输出，xlf是PA 的输入，即预失真器的输出。

在每次“后失真器”进行更新后，将“后失真器”中并联FIR 滤波器组的参数复制给预失真器中相应的部分。

5 仿真分析

本文采用MATLAB 对预失真系统进行仿真实验，以验证本文所提出的预失真结构的可行性和有效性。

本仿真实验中PA 采用Wiener 模型［10］，LTI 部分由3 阶的FIR 来描述，系数分别为a=［0.769 2 0.153 8 0.076 9］;NL 部分由仅含奇次幂的5 阶多项式描述，系数分别为b=［14.974 0+j0.051 9－23.095 4 +j4.968 0 21.393 6 +j0.430 5］，并进行归一化处理，即使Wiener 模型的输入信号和输出信号的取值范围皆在0 与1 之间。

系统采用16QAM 调制信号作为输入信号，波形成形采用的是升余弦滚降滤波器，其参数分别为滚降系数为0.5，延迟为3，升采样率为8。通过滤波器成形后的信号需要进行归一化处理，使输出的采样值信号的最大包络值为1，并对归一化后的信号进过峰值回退(PBO)处理，PBO 值为0.9。

仿真实验中，Hammerstein 预失真器中NL 子系统和LTI 子系统分别由LUT 和并联FIR 滤波器组实现，在算法第一步为了去除AM/AM 和AM/PM曲线的扩散，采用1000 个数据作为训练序列，Nam(13)=Npm(16)=256，α(15)=0.9。LTI 部分，M=2，L1=16，L2=8，μ(18)=0.01，FIR 滤波器的冲激响应初始化为单位脉冲。

图6 是系统输入信号、仅经PA 放大的信号、经过本文提出的PD 和PA(简记为PD+PA)输出的信号星座图。从该图可以看出，本文提出的Hammerstein 预失真器能够有效地克服由PA 非线性和记忆效应引起的信号星座图的偏转和扩散。

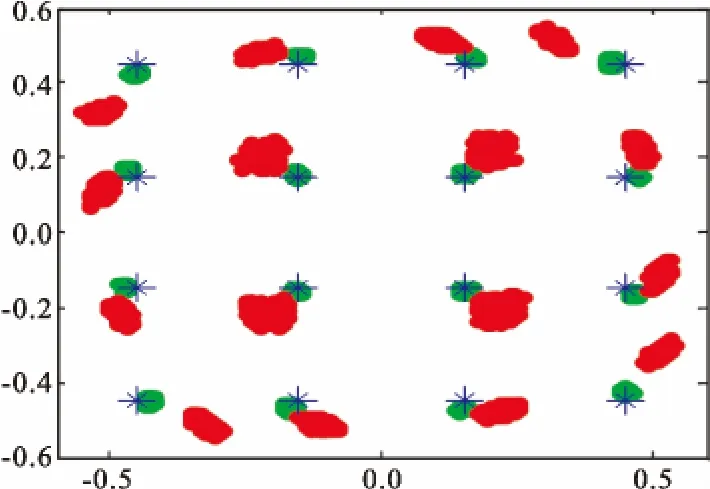
图6 星座图Fig.6 Constellation diagram

图7 所示为采用以下3 种PD 的MSE 系统学习曲线:一是无记忆PD，采用本文辨识PD 第一步时所采用的LUT 算法;二是一种传统的Hammerstein预失真器，由LUT 级联高阶FIR 滤波器实现，仿真中采用的是32 阶FIR 滤波器;三是本文提出的采用LUT 级联并联FIR 滤波器组作为其实现形式的Hammerstein 预失真器。需要说明的是，为了更清晰地显示3 条曲线的区别，我们对图中的均方误差(Mean Squared Error，MSE)曲线皆进行了适当的平滑处理。由图7 可以看到，本文提出的Hammerstein预失真器比第2 种Hammerstein 预失真器有更好的效果，MSE 约降低2 dB，但却比第2 种预失真器具有更低的模型复杂度，但也应注意到本文提出的Hammerstein 预失真器的收敛速度相对较慢。

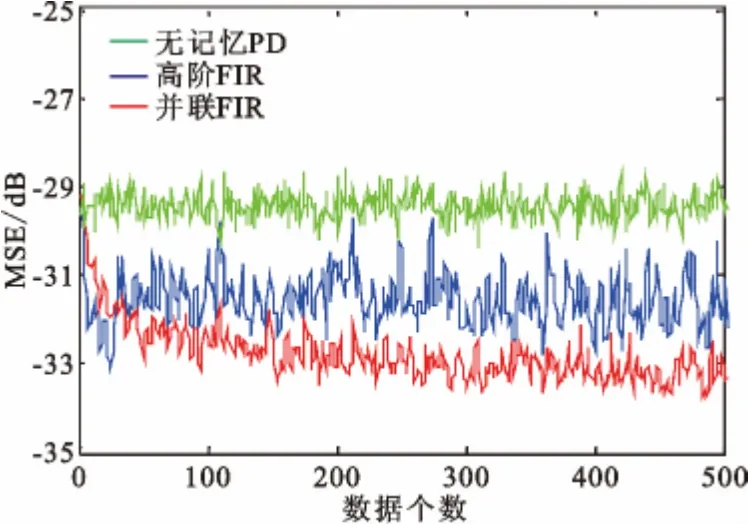
图7 MSE 曲线Fig.7 MSE curves

图8 为输入信号即理想输出信号、仅经过PA 的输出信号、由LUT 级联高阶FIR 滤波器实现的Hammerstein 预失真器的输出信号、本文提出的Hammerstein 预失真器级联PA 的输出信号的功率谱密度(Power Spectral Density，PSD)曲线。由图8(a)可以看到，本文提出的Hammerstein 预失真器能够对由PA非线性和记忆效应引起带外失真起到有效的抑制作用，但与一般的Hammerstein 预失真器相比效果不明显。为了进一步验证本文提出预失真器的有效性，将PA 的2 阶记忆长度的Wiener 模型换为记忆长度为3阶的Wiener 模型(非线性部分参数不变，线性部分的参数a=［0.569 2 0.2 0.153 8 0.076 9］)。此时，用于对比的Hammerstein 预失真器的LTI 部分由64 阶FIR 滤波器实现，本文提出的Hammerstein 预失真器的LTI 部分，M=3，L1=16，L2=8，L3=4。得到新的一组PSD 曲线如图8(b)所示，由图可知本文提出的Hammerstein 预失真器对强记忆效应的PA 的补偿更加有效。

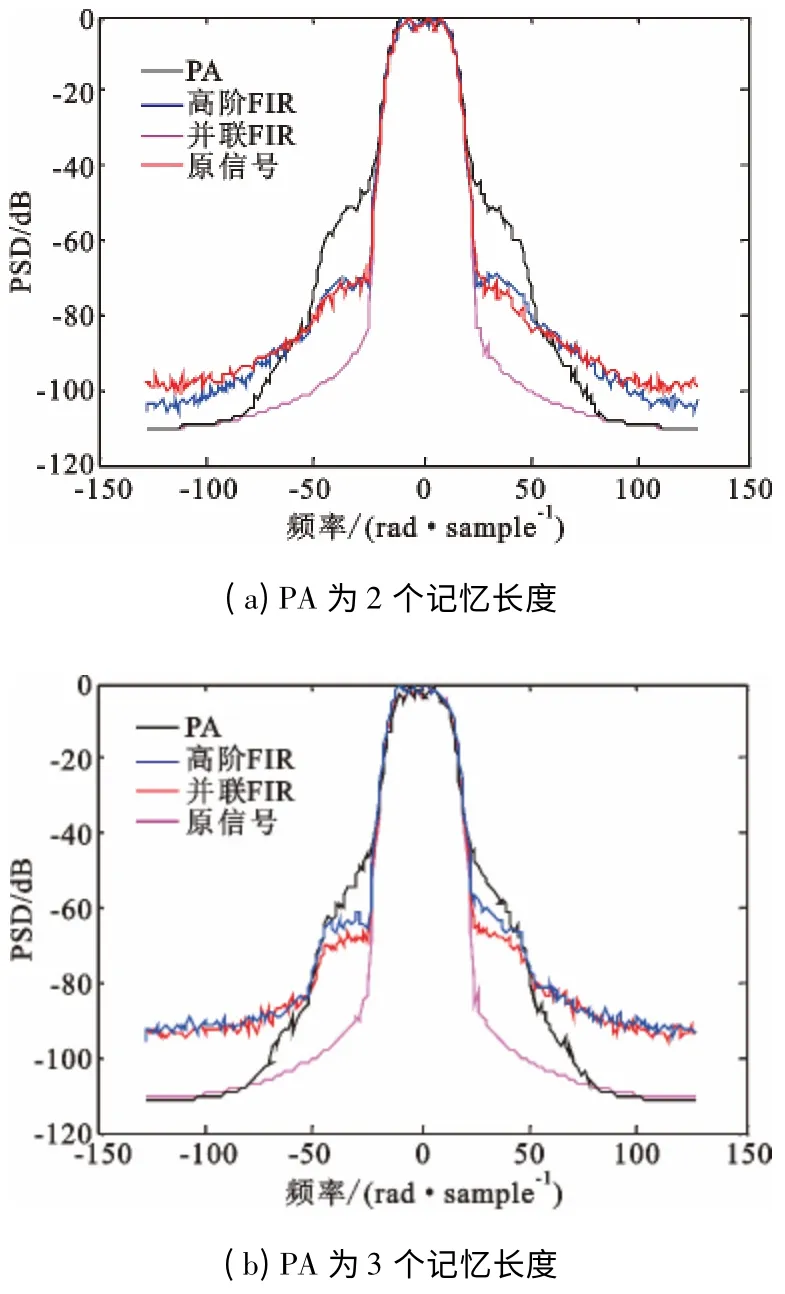
图8 PSD 曲线Fig.8 PSD curves

仿真实验及结果可以证明，本文提出的Hammerstein 预失真器能够对带强记忆效应PA 的非线性失真进行更有效的补偿。

6 结论

针对目前Hammerstein 预失真器对PA 逆记忆效应描述不充分的问题，本文提出了一种以LUT 级联并联FIR 滤波器组作为其实现形式的Hammerstein 预失真器，并采用一种两步算法对其参数进行辨识。与传统的Hammerstein 预失真器及前期工作［5，9］相比，该预失真器以较低的模型复杂度较好地实现了对带记忆效应PA 非线性失真的补偿，尤其是对带强记忆效应的PA 的补偿，仿真实验证明了其有效性。

［1］ERMOLOVA N Y，TIRKKONEN O.Theoretical characterization of memory polynomial models with Gaussian inputs［J］.IEEE Signal Processing Letters，2009，16(8):651－654.

［2］CHOI S，JEONG E，LEE Y H.Adaptive predistortion with direct learning based on piecewise linear approximation of amplifier nonlinearity［J］.IEEE Journal on Selected Topics in Signal Processing，2009，3(3):397－404.

［3］LIU Y J，CHEN W H，ZHOU J，et al.Digital Predistorter for Concurrent Dual－ Band Transmitters Using 2－ D Modified Memory Polynomials［J］.IEEE Transactions on Microwave Theory and Techiques，2013，61(1):281－290.

［4］RAWAT M，GHANNOUCHI F M，RAWAT K.Three－Layered Biased Memory Polynomial for Dynamic Modeling and Predistortion of Transmitters with Memory［J］.IEEE Transactions on Circuits and Systems，2013，60 (3):768－777.

［5］佀秀杰，金明录.一种新的用于Hammerstein 预失真器的自适应结构［J］.电子与信息学报，2011，33(6):1345－1349.SI Xiujie，JIN Minglu.A novel adaptive structure for Hammerstein predistorter［J］.Journal of Electronics ＆ Information Technology，2011，33(6):1345－1349.(in Chinese)

［6］MKADEM F，BOUMAIZA S.Extended Hammerstein behavioral model using artificial neural networks［J］.IEEE Transactions on Microwave Theory and Techniques，2009，57(4):745－751.

［7］LIU L J，BOUMAIZA S，GHANNOUCHI F M.Augmented Hammerstein Predistorter for Linearization of Broad－Band Wireless Transmitters［J］.IEEE Transactions on Microwave and Techniques，2006，54(4):1340－1349.

［8］ZHAI J F，ZHOU J Y，ZHANG L，et al.Dynamic behavioral modeling of power amplifiers using ANFIS－ based Hammerstein［J］.IEEE Microwave and Wireless Components Letters，2008，18(10):704－706.

［9］佀秀杰，金明录，刘文龙.一种基于滤波器矩阵的Hammerstein 预失真器［J］.大连理工大学学报，2011，51(3):428－432.SI Xiujie，JIN Minglu，LIU Wenlong.A Hammerstein predistorter based on filter matrix［J］.Journal of Dalian University of Technology，2011，51(3):428－432.(in Chinese)

［10］MARTIN S.The Volterra and Wiener Theories of Nonlinear System［M］.New York:Wiley and Sons，1980.